


还剩31页未读,
继续阅读
第六章 几何图形初步 章末小结 课件 2024-2025学年人教版七年级数学上册
展开
这是一份第六章 几何图形初步 章末小结 课件 2024-2025学年人教版七年级数学上册,共39页。
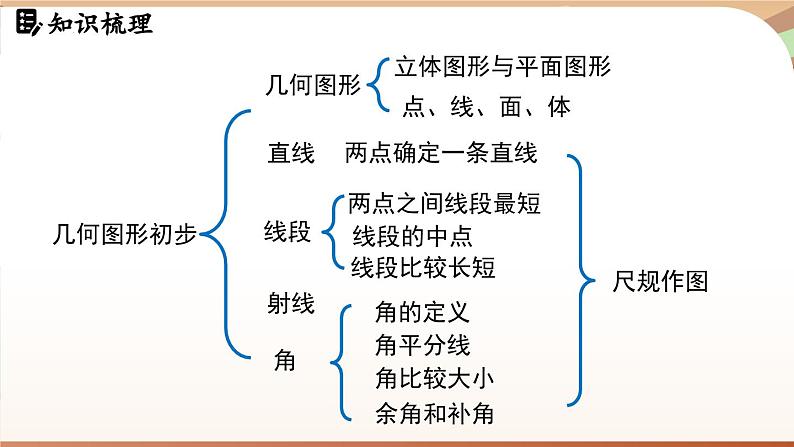
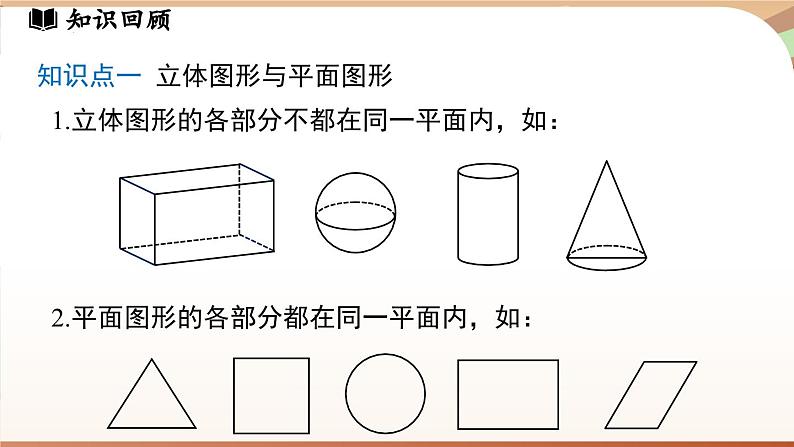
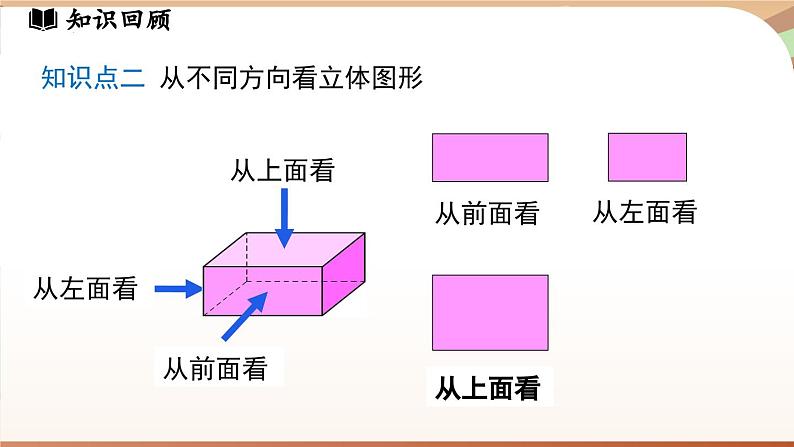
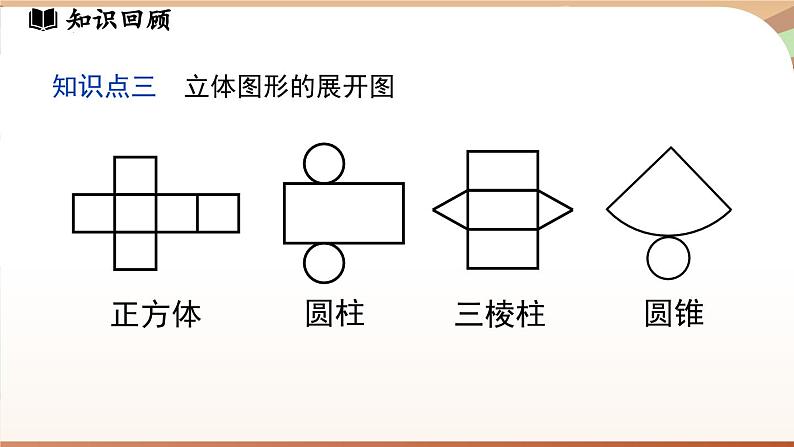
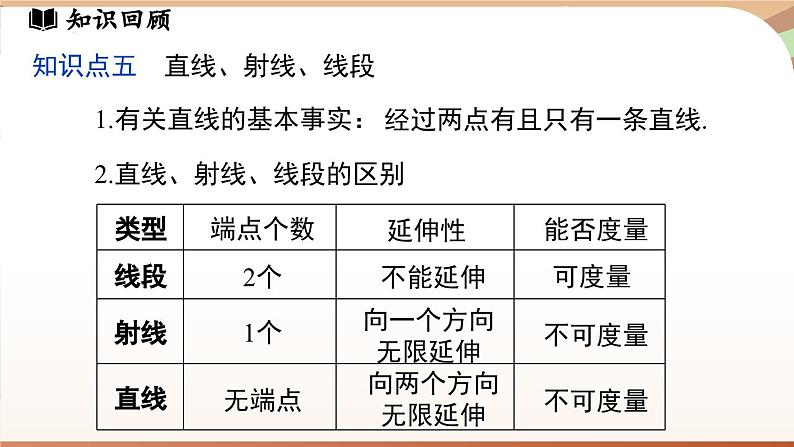
第六章 几何图形初步章末小结知识梳理几何图形初步直线线段线段的中点角的定义两点之间线段最短射线角角平分线两点确定一条直线线段比较长短角比较大小尺规作图余角和补角几何图形点、线、面、体立体图形与平面图形知识回顾知识点一 立体图形与平面图形1.立体图形的各部分不都在同一平面内,如:2.平面图形的各部分都在同一平面内,如:知识回顾知识点二 从不同方向看立体图形 从上面看从前面看从左面看从上面看从左面看从前面看知识回顾知识点三 立体图形的展开图正方体圆柱三棱柱圆锥知识回顾知识点四 点、线、面、体之间的联系1.体是由面围成,面与面相交成线,线与线相交成点;2.点动成线、线动成面、面动成体.知识回顾知识点五 直线、射线、线段1.有关直线的基本事实:经过两点有且只有一条直线.2.直线、射线、线段的区别端点个数2个不能延伸延伸性能否度量可度量1个向一个方向无限延伸不可度量无端点向两个方向无限延伸不可度量知识回顾4.有关线段的基本事实:两点之间,线段最短.3.线段的中点5.连接两点的线段的长度,叫作这两点间的距离.几何语言:知识点五 直线、射线、线段知识回顾知识点六 角1.角的定义(1)有公共端点的两条射线组成的图形,叫作角;(2)角也可以看作由一条射线绕着它的端点旋转而形成的图形.2.角的度量度、分、秒的互化:1°=60′,1′=60″知识回顾知识点六 角3.角的平分线C几何语言:知识回顾知识点七 余角和补角(1)定义 ①如果两个角的和等于90°(直角),就说这两个角互为余角(简称这两个角互余). ②如果两个角的和等于180°(平角),就说这两个角互为补角(简称这两个角互补 ).(2)性质 ①同角 (等角)的余角相等. ②同角 (等角)的补角相等.重难剖析1.根据下列多面体的平面展开图,填写多面体的名称. (1)_______,(2)_______,(3)________.长方体三棱柱三棱锥(1) (2) (3)重难剖析2 .将下面的平面图形绕轴旋转一周,得到的立体图形是( )C旋转轴A B C D重难剖析3.如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.请画出这个几何体从前面、左面、上面看到的形状图.从前面看从左面看从上面看解:如图所示.重难剖析4.下列叙述正确的是( A )A重难剖析5.如图,一共有 1条直线,是 直线A C;能用字母表示的射线有 7 条,它们分别是射线 DA,DC,BA,B C,DB, AC ,其中在同一条直线上的射线是射线 D ADDC , .17 DA,DC,BA,BC,DB,AC(或AD),CA(或CD) DA,DC,AC(或AD),CA(或CD) 直线AC(或直线AD,或直线CD)重难剖析6.如图,线段AB=32 cm,点C在AB上,且AC∶CB=5∶3,点D是AC的中点,点O是AB的中点,求DB与OC的长. 重难剖析 重难剖析 重难剖析7.下午2时15分到5时30分,时钟的时针转过的度数为______.分析:时钟被分成12个大格,相当于把圆分成12等份,每一等份等于30°.分针转360°时,时针转一格,即30°.从2时15分到5时30分,时针走了(5.5-2.25)格,即30°×(5.5-2.25)=97.5°.97.5°重难剖析8.如图,∠AOB=∠COD=90° ,∠BOC=42° ,则∠AOD=( )A.48° B.148°C.138° D.128°分析:由图可知∠AOB,∠BOC,∠COD,∠AOD组成一个周角,所以∠AOD=360°-∠AOB-∠COD-∠BOC=138°.故选C.C重难剖析9.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( ) A. B. C. D.A∠α与∠β互余∠α =∠β∠α =∠β∠α与∠β互补重难剖析10. 如图,直线AB,CD相交于点O,OA平分∠EOC. (1) 若∠EOC=70°,求∠BOD的度数; 解:(1)因为直线AB,CD相交于点O,所以∠AOC=∠BOD.因为OA平分∠EOC,所以∠BOD =∠AOC =35°.重难剖析(2) 若∠EOC∶ ∠EOD=2∶3,求∠BOD的度数. 重难剖析11.一只蚂蚁从 O 点出发,沿东北方向爬行 2.5 cm,碰到障碍物 B 后,折向北偏西60°方向爬行3 cm到 C点. 画出蚂蚁的爬行路线.北OB2.5 cmC3 cm60°45°解:如图所示.能力提升1.将下图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )A.B.C.D.C能力提升2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?从前面看从上面看能力提升2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?从前面看从上面看1111132最少摆法示意图(不唯一)能力提升2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?从前面看从上面看3332221最多摆法示意图能力提升最少摆法(不唯一)所需小立方块个数:3+2+1+1+1+1+1=10(个).最多摆法所需小立方块个数:3+3+3+2+2+2+1=16 (个).解:如图所示.能力提升 3.如图,已知线段AB=a,点O是线段AB上的动点,且不与点A,B重合,点C,D分别是线段OA,OB的中点.(1)求线段CD的长.(2)当点O在线段AB的延长线上时,其他条件不变,请画出图形,并求出 CD的长;比较(1)(2)的结果,你发现了什么规律?A C O D B能力提升 A C B D O能力提升双中点线段长度计算规律(1)线段上的一点把线段分成两条线段,这两条线段的中点间的距离等于原线段长度的一半;(2)线段延长线上的一点和原线段的两个端点构成两条线段,这两条线段的中点间的距离等于原线段长度的一半.能力提升4. 如图,将一张长方形纸片分别沿着EP,FP折,使点B落在点B',点C落在点C'.若点P,B',C'不在一条直线上,且两条折痕的夹角∠EPF=85°,则∠ B'PC'= .10° 能力提升分析:由折叠可知∠BPE=∠B'PE , ∠CPF=∠C'PF ,所以2∠B'PE+2∠C'PF-∠B'PC'=180° ,即2(∠B'PE+∠C'PF)-∠B'PC'=180° .又因为∠EPF=∠B'PE+∠C'PF-∠B'PC'=85° ,所以∠B'PE+∠C'PF=∠B'PC'+85° ,所以2(∠B'PC'+85°)-∠B'PC'=180° ,解得∠B'PC'=10° .能力提升5.已知点O是直线AB 上一点,∠COD 是直角,OE 平分∠BOC.(1) 如图1,若∠AOC=30°,则∠DOE 的度数为 15° ;15° 能力提升(2) 在图1中,若∠AOC=α,求∠DOE的度数; 能力提升解:(3)因为∠COD是直角,所以∠COD=∠COE+∠DOE=90°,所以2∠COE+2∠DOE=180°.因为OE平分∠BOC,所以∠COE=∠BOE.所以∠BOC+∠AOC=2∠COE+∠AOC=180°.所以2∠COE+2∠DOE=2∠COE+∠AOC.所以∠AOC=2∠DOE.(3) 如图2的位置关系,探究∠AOC 与∠DOE 之间的数量关系.能力提升6.已知∠α和∠β互为补角,并且∠β的一半比∠α小30°,求∠α,∠β. 解:设∠α=x°,则∠β=180°-x°.根据题意,得∠β=2(∠α-30°),得180-x=2(x-30),解得x=80.所以∠α=80°,∠β=100°.提示:此题的和差倍分关系较复杂,可列方程解答.
第六章 几何图形初步章末小结知识梳理几何图形初步直线线段线段的中点角的定义两点之间线段最短射线角角平分线两点确定一条直线线段比较长短角比较大小尺规作图余角和补角几何图形点、线、面、体立体图形与平面图形知识回顾知识点一 立体图形与平面图形1.立体图形的各部分不都在同一平面内,如:2.平面图形的各部分都在同一平面内,如:知识回顾知识点二 从不同方向看立体图形 从上面看从前面看从左面看从上面看从左面看从前面看知识回顾知识点三 立体图形的展开图正方体圆柱三棱柱圆锥知识回顾知识点四 点、线、面、体之间的联系1.体是由面围成,面与面相交成线,线与线相交成点;2.点动成线、线动成面、面动成体.知识回顾知识点五 直线、射线、线段1.有关直线的基本事实:经过两点有且只有一条直线.2.直线、射线、线段的区别端点个数2个不能延伸延伸性能否度量可度量1个向一个方向无限延伸不可度量无端点向两个方向无限延伸不可度量知识回顾4.有关线段的基本事实:两点之间,线段最短.3.线段的中点5.连接两点的线段的长度,叫作这两点间的距离.几何语言:知识点五 直线、射线、线段知识回顾知识点六 角1.角的定义(1)有公共端点的两条射线组成的图形,叫作角;(2)角也可以看作由一条射线绕着它的端点旋转而形成的图形.2.角的度量度、分、秒的互化:1°=60′,1′=60″知识回顾知识点六 角3.角的平分线C几何语言:知识回顾知识点七 余角和补角(1)定义 ①如果两个角的和等于90°(直角),就说这两个角互为余角(简称这两个角互余). ②如果两个角的和等于180°(平角),就说这两个角互为补角(简称这两个角互补 ).(2)性质 ①同角 (等角)的余角相等. ②同角 (等角)的补角相等.重难剖析1.根据下列多面体的平面展开图,填写多面体的名称. (1)_______,(2)_______,(3)________.长方体三棱柱三棱锥(1) (2) (3)重难剖析2 .将下面的平面图形绕轴旋转一周,得到的立体图形是( )C旋转轴A B C D重难剖析3.如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.请画出这个几何体从前面、左面、上面看到的形状图.从前面看从左面看从上面看解:如图所示.重难剖析4.下列叙述正确的是( A )A重难剖析5.如图,一共有 1条直线,是 直线A C;能用字母表示的射线有 7 条,它们分别是射线 DA,DC,BA,B C,DB, AC ,其中在同一条直线上的射线是射线 D ADDC , .17 DA,DC,BA,BC,DB,AC(或AD),CA(或CD) DA,DC,AC(或AD),CA(或CD) 直线AC(或直线AD,或直线CD)重难剖析6.如图,线段AB=32 cm,点C在AB上,且AC∶CB=5∶3,点D是AC的中点,点O是AB的中点,求DB与OC的长. 重难剖析 重难剖析 重难剖析7.下午2时15分到5时30分,时钟的时针转过的度数为______.分析:时钟被分成12个大格,相当于把圆分成12等份,每一等份等于30°.分针转360°时,时针转一格,即30°.从2时15分到5时30分,时针走了(5.5-2.25)格,即30°×(5.5-2.25)=97.5°.97.5°重难剖析8.如图,∠AOB=∠COD=90° ,∠BOC=42° ,则∠AOD=( )A.48° B.148°C.138° D.128°分析:由图可知∠AOB,∠BOC,∠COD,∠AOD组成一个周角,所以∠AOD=360°-∠AOB-∠COD-∠BOC=138°.故选C.C重难剖析9.如图,将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( ) A. B. C. D.A∠α与∠β互余∠α =∠β∠α =∠β∠α与∠β互补重难剖析10. 如图,直线AB,CD相交于点O,OA平分∠EOC. (1) 若∠EOC=70°,求∠BOD的度数; 解:(1)因为直线AB,CD相交于点O,所以∠AOC=∠BOD.因为OA平分∠EOC,所以∠BOD =∠AOC =35°.重难剖析(2) 若∠EOC∶ ∠EOD=2∶3,求∠BOD的度数. 重难剖析11.一只蚂蚁从 O 点出发,沿东北方向爬行 2.5 cm,碰到障碍物 B 后,折向北偏西60°方向爬行3 cm到 C点. 画出蚂蚁的爬行路线.北OB2.5 cmC3 cm60°45°解:如图所示.能力提升1.将下图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )A.B.C.D.C能力提升2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?从前面看从上面看能力提升2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?从前面看从上面看1111132最少摆法示意图(不唯一)能力提升2.用小立方块搭一个几何体,使得它从前面看和从上面看得到的图,如图所示.这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?从前面看从上面看3332221最多摆法示意图能力提升最少摆法(不唯一)所需小立方块个数:3+2+1+1+1+1+1=10(个).最多摆法所需小立方块个数:3+3+3+2+2+2+1=16 (个).解:如图所示.能力提升 3.如图,已知线段AB=a,点O是线段AB上的动点,且不与点A,B重合,点C,D分别是线段OA,OB的中点.(1)求线段CD的长.(2)当点O在线段AB的延长线上时,其他条件不变,请画出图形,并求出 CD的长;比较(1)(2)的结果,你发现了什么规律?A C O D B能力提升 A C B D O能力提升双中点线段长度计算规律(1)线段上的一点把线段分成两条线段,这两条线段的中点间的距离等于原线段长度的一半;(2)线段延长线上的一点和原线段的两个端点构成两条线段,这两条线段的中点间的距离等于原线段长度的一半.能力提升4. 如图,将一张长方形纸片分别沿着EP,FP折,使点B落在点B',点C落在点C'.若点P,B',C'不在一条直线上,且两条折痕的夹角∠EPF=85°,则∠ B'PC'= .10° 能力提升分析:由折叠可知∠BPE=∠B'PE , ∠CPF=∠C'PF ,所以2∠B'PE+2∠C'PF-∠B'PC'=180° ,即2(∠B'PE+∠C'PF)-∠B'PC'=180° .又因为∠EPF=∠B'PE+∠C'PF-∠B'PC'=85° ,所以∠B'PE+∠C'PF=∠B'PC'+85° ,所以2(∠B'PC'+85°)-∠B'PC'=180° ,解得∠B'PC'=10° .能力提升5.已知点O是直线AB 上一点,∠COD 是直角,OE 平分∠BOC.(1) 如图1,若∠AOC=30°,则∠DOE 的度数为 15° ;15° 能力提升(2) 在图1中,若∠AOC=α,求∠DOE的度数; 能力提升解:(3)因为∠COD是直角,所以∠COD=∠COE+∠DOE=90°,所以2∠COE+2∠DOE=180°.因为OE平分∠BOC,所以∠COE=∠BOE.所以∠BOC+∠AOC=2∠COE+∠AOC=180°.所以2∠COE+2∠DOE=2∠COE+∠AOC.所以∠AOC=2∠DOE.(3) 如图2的位置关系,探究∠AOC 与∠DOE 之间的数量关系.能力提升6.已知∠α和∠β互为补角,并且∠β的一半比∠α小30°,求∠α,∠β. 解:设∠α=x°,则∠β=180°-x°.根据题意,得∠β=2(∠α-30°),得180-x=2(x-30),解得x=80.所以∠α=80°,∠β=100°.提示:此题的和差倍分关系较复杂,可列方程解答.
相关资料
更多









