山东省菏泽市巨野县实验中学2024-2025学年高一上学期入学分班考数学试题（原卷版+解析版）

这是一份山东省菏泽市巨野县实验中学2024-2025学年高一上学期入学分班考数学试题（原卷版+解析版），文件包含山东省菏泽市巨野县实验中学2024-2025学年高一上学期入学分班考数学试题原卷版docx、山东省菏泽市巨野县实验中学2024-2025学年高一上学期入学分班考数学试题解析版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。

1. 下列各数中，最小的数是（ ）
A. -2B. C. D.
【答案】A
【解析】
【分析】根据实数大小比较即可求解．
【详解】,
因为,
所以最小的是为-2，
故选：A.
2. 下列运算正确的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】根据合并同类项、同底数幂的除法、积的乘方的运算法则计算即可．
【详解】对于A，，运算错误，该选项不符合题意；
对于B，，运算错误，该选项不符合题意；
对于C，，运算正确，该选项符合题意；
对于D，，运算错误，该选项不符合题意．
故选：C.
3. 2024年3月份，低空经济首次被写入《政府工作投告》．截止2023年底，全国注册通航企业690家、无人机万架，运营无人机的企业达万家．将万用科学记数法表示为（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】根据科学记数法的定义表示出来即可.
【详解】万,
故选：B.
4. 关于的一元二次方程有实数根，则实数的取值范围是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据一元二次方程有实数根的条件是，由此列不等式求解即得．
【详解】因关于的一元二次方程有实数根，
故，解得．
故选：B．
5. 已知点在反比例函数的图象上，则的大小关系是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】根据反比例函数的性质得到函数的图象分布在第二、四象限，在每一象限，y随x的增大而增大，结合三点的横坐标即可求解.
【详解】因为，所以函数的图象分布在第二、四象限，
在每一象限，y随x的增大而增大，因为，所以，
所以.
故选：C.
6. 同一条公路连接，，三地，地在，两地之间．甲、乙两车分别从地、地同时出发前往地．甲车速度始终保持不变，乙车中途休息一段时间，继续行驶．下图表示甲、乙两车之间的距离（）与时间（）的函数关系．下列结论正确的是（ ）

A. 甲车行驶与乙车相遇B. ，两地相距
C. 甲车的速度是D. 乙车中途休息分钟
【答案】A
【解析】
【分析】根据函数的图象对选项进行分析，从而确定正确答案.
【详解】根据函数图象可得两地之间的距离为（），两车行驶了小时，同时到达地，
如图所示，在小时，两车同向运动，在第2小时，即点时，两车距离发生改变，此时乙车休息，
点的意义是两车相遇，点意义是乙车休息后再出发，

∴乙车休息了1小时，故D不正确，
设甲车的速度为，乙车的速度为，
根据题意，乙车休息后两车同时到达地，则甲车速度比乙车的速度慢，，
∵，即，
在时，乙车不动，则甲车的速度是，
∴乙车速度为，故C不正确，
∴的距离为千米，故B不正确，
设小时两辆车相遇，依题意得，，
解得：，即小时时，两车相遇，故A正确.
故选：A
7. 《九章算术》是我国古老的数学经典著作，书中提到这样一道题目：以绳测井．若将绳三折测之，绳多四尺；若将绳四折测之，绳多一尺．绳长、井深各几何？题目大意是：用绳子测量水井的深度．如果将绳子折成三等份，一份绳长比井深多尺；如果将绳子折成四等份，一份绳长比井深多尺．绳长、井深各是多少尺？若设绳长尺，井深尺，则符合题意的方程组是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】阅读条件找出等量关系可得方程组即可．
【详解】设绳长x尺，井深y尺，
依题意，得：．
故选：C
8. 如图，中，，分别以顶点A，为圆心，大于的长为半径画弧，两弧分别相交于点和点，作直线分别与，交于点和点；以点A为圆心，任意长为半径画弧，分别交，于点和点，再分别以点，点为圆心，大于的长为半径画弧，两弧交于点，作射线，若射线恰好经过点，则下列四个结论：①；②垂直平分线段；③；④．其中，正确结论的个数有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
【分析】由作图可知垂直平分线段、平分，进而证明可判定①；再说明可得垂直平分线段可判定②；根据直角三角形的性质可得可判定③，根据三角形的面积公式即可判定④．
【详解】由作图可知垂直平分线段，
∴，
∴，
由作图可知平分，
∴，
∵，
∴，故①正确，
∴，
∵，
∴，
∴垂直平分线段，故②正确，
∵，
∴，故③正确，
∴，
∵，
∴，
∴，故④正确．
故选：D.
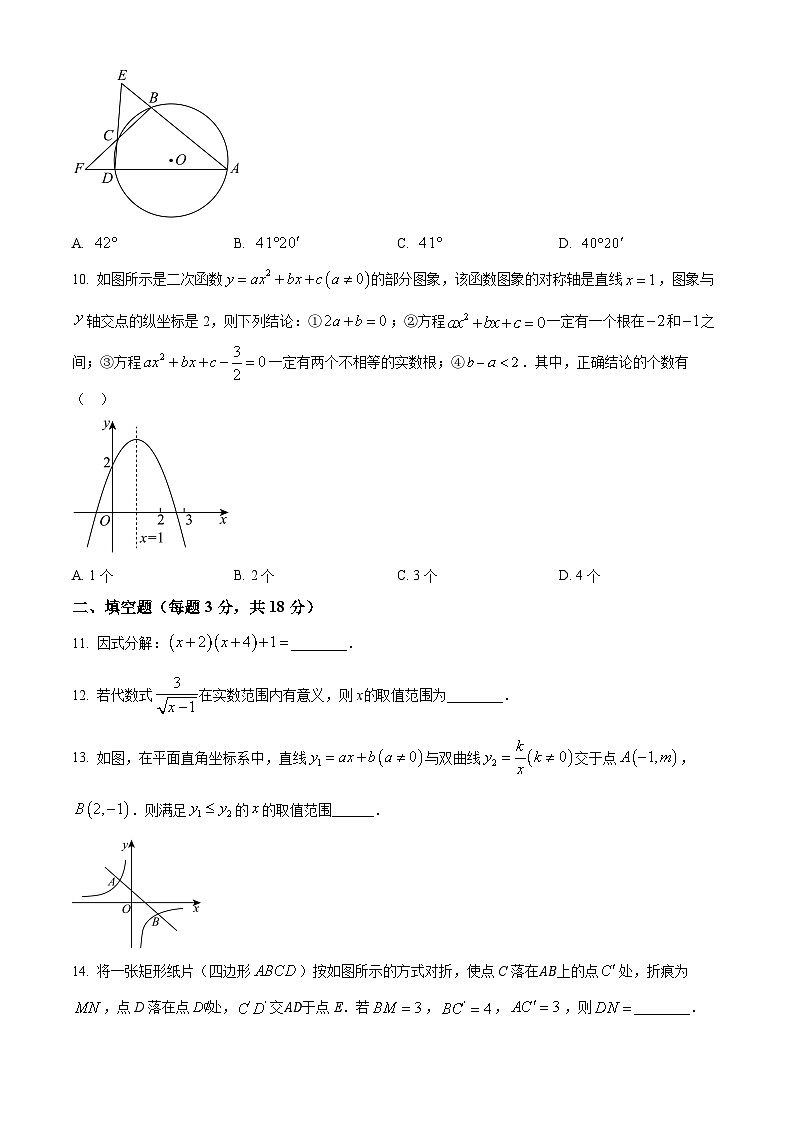
9. 如图，分别延长圆内接四边形的两组对边，延长线相交于点E，F.若，，则的度数为（ ）

A. B. C. D.
【答案】C
【解析】
【分析】根据“圆的内接四边形对角互补”可得，.根据三角形外角定理可得，，由此可得，又由，可得，即可得解.
【详解】∵四边形是的内接四边形，
∴，，
，，
，
，，，
，解得，
，.
故选：C
10. 如图所示是二次函数的部分图象，该函数图象的对称轴是直线，图象与轴交点的纵坐标是2，则下列结论：①；②方程一定有一个根在和之间；③方程一定有两个不相等的实数根；④．其中，正确结论的个数有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
【分析】根据抛物线与坐标轴的交点情况、二次函数与方程的关系、二次函数的性质逐个判断即可．
【详解】抛物线的对称轴为直线，即，则，，①正确；
抛物线的对称轴为直线，与x轴的一个交点在2、3之间，
则与x轴的另一个交点在、0之间，方程一定有一个根在和0之间，②错误；
抛物线与直线有两个交点，则方程一定有两个不相等的实数根，③正确；
抛物线与x轴的另一个交点在，0之间，则，又图象与y轴交点的纵坐标是2，
则，即，于是，④错误，
所以①③正确，共2个．
故选：B
二、填空题（每题3分，共18分）
11. 因式分解：________．
【答案】
【解析】
【分析】先按照多项式乘以多项式展开，然后利用完全平方公式分解因式即可．
【详解】.
故答案为：.
12. 若代数式在实数范围内有意义，则x的取值范围为________．
【答案】x>1
【解析】
【分析】根据分式的分母不为0，二次根式的被开方数为非负数，进行求解即可．
【详解】依题意,
解得x>1.
故答案为：x>1.
13. 如图，在平面直角坐标系中，直线与双曲线交于点，．则满足的的取值范围______．

【答案】或
【解析】
【分析】本题考查了一次函数与反比例函数的交点问题，根据图象解答即可求解，利用数形结合思想解答是解题的关键．
【详解】由题意可知，在双曲线上，
故，则.
故.
由图象可得，当或时，，
故填：或
14. 将一张矩形纸片（四边形）按如图所示的方式对折，使点C落在AB上的点处，折痕为，点D落在点处，交AD于点E．若，，，则________．
【答案】32
【解析】
【分析】先根据勾股定理求出，然后证明，得到，，即可得到，，然后在中，利用解题即可．
【详解】在中，，
由折叠可得，，
又是矩形，则，，
于是，又，则，
因此，，
，，
，，
设，则，在中，，即，
所以.
故答案为：
15. 如图①是半径为1的圆，在其中挖去2个半径为的圆得到图②，挖去个半径为的圆得到图③……，则第个图形阴影部分的面积是______.

【答案】
【解析】
【分析】分别求出图②与图③中阴影部分面积，再从中发现规律，然后根据规律即可得出第个图形阴影部分的面积.
【详解】图②中阴影部分的面积为：；
图③中阴影部分的面积为：；
图④是半径为1的圆，在其中挖去个半径为的圆得到的，
则图④中阴影部分的面积为：；
…，
则第个图形阴影部分的面积为：.
故答案为：
16. 在平面直角坐标系中，抛物线的图象如图所示．已知点坐标为，过点作轴交抛物线于点，过点作交抛物线于点，过点作轴交抛物线于点，过点作交抛物线于点……，依次进行下去，则点的坐标为_____．
【答案】
【解析】
【分析】根据二次函数性质可得出点的坐标，求得直线为，联立方程求得的坐标，即可求得的坐标，同理求得的坐标，即可求得的坐标，根据坐标的变化找出变化规律，即可找出点的坐标．
【详解】解：∵点坐标为，
∴直线为，，
∵，
∴直线为，
解得或，
∴，
∴，
∵，
∴直线为，
解得或，
∴，
∴
…，
∴，
故答案为：
三、解答题
17. （1）计算：；
（2）先化简，再求值：，其中.
【答案】（1）；（2），
【解析】
【分析】（1）先化简立方根，负指数，绝对值，再相加减；
（2）先括号内通分，分子分解因式，除法换作乘法，约分化简，再代入a值，合并即得．
【详解】（1）
；
（2）
；
当时，
原式.
18. 如图1，在中，点，在边上，，.
（1）求证：.
（2）如图2，用直尺和圆规在直线上取点，点（点在点的左侧），使得，且（不写作法，保留作图痕迹）；
（3）如图3，用直尺和圆规在直线上取一点，在直线上取一点，使得，且（不写作法，保留作图痕迹）.
【答案】（1）证明见解析
（2）作图见解析 （3）作图见解析
【解析】
【分析】（1）根据全等三角形的判定定理和性质定理，证明即可；
（2）由（1）的结论，通过证明，再利用全等三角形的性质定理，证明,尺规作图即可；
（3）在（2）的基础上，先证明，再利用全等三角形的性质定理即可.
【小问1详解】
∵，∴.
在和中，
，
∴(SAS)，
∴．
【小问2详解】
以点为圆心，以长度为半径作弧，交直线于一点，该点即为点，以点为圆心，以长度为半径作弧，交直线于一点，该点即为点，连接，，图形如图所示．
【小问3详解】
以点为圆心，以长为半径作弧，交的延长线于一点，该点即为点，
以点为圆心，以长为半径作弧，交直线于一点，该点即为点，连接，
图形如图所示．
根据作图可得：，
又∵，
∴，
∴.
19. 在全民健身运动中，骑行运动颇受市民青睐，甲、乙两骑行爱好者约定从地沿相同路线骑行去距地30千米的地，已知甲骑行的速度是乙的1.2倍．若乙先骑行2千米，甲才开始从地出发，则甲出发半小时恰好追上乙，求甲骑行的速度；
【答案】千米/时；
【解析】
【分析】设乙的速度为千米/时，则甲的速度为千米/时，根据甲出发半小时恰好追上乙列方程求解即可；
【详解】设乙的速度为千米/时，则甲的速度为千米/时，
由题意得：，
解得：，则，
答：甲骑行的速度为千米/时；
20. 直线与反比例函数的图象相交于点，，与轴交于点．
（1）求直线的表达式；
（2）若，请直接写出满足条件的的取值范围；
（3）过点作轴的平行线交反比例函数的图象于点，求的面积．
【答案】（1）
（2）或
（3）
【解析】
【分析】（1）分别将点、点代入，求出m、n值，再分别代入中即可解答；
（2）根据函数图像确定不等式的解集即可；
（3）先把代入中，求出点D的坐标，再根据三角形的面积公式计算即可．
【小问1详解】
分别将点、点代入中，
可得：，，
解得：，，
点坐标为，点坐标为，
把点坐标，点坐标分别代入，
可得，
解得：，
一次函数表达式为．
【小问2详解】
∵直线与反比例函数的图象相交于点，
∴由图象可知，当时，或．
【小问3详解】
把时代入中，得，
点坐标为，
即，
．
21. 如图①是位于嘉峪关市雄关广场转盘中心的象征这座城市的雄关之光，于2001年6月建成，其形如长剑指天，寓意亲手创造了戈壁钢城的嘉峪关人坚韧不拔，奋发向上，继续创建嘉峪关更加辉煌明天的美好愿望.某校实践小组把“测量雄关之光雕塑的高度”作为一项活动课题，并设计了如下的测量方案.
请根据以上测量数据，计算雄关之光雕塑的高度.（结果保留整数）（参考数据：，，，，，）
【答案】39米
【解析】
【分析】根据垂直的定义得到，根据三角函数的定义得到（米），（米)，于是得到结论。
【详解】，
，
在中，，米，
（米，
在中，，米，
（米，
（米，
答：雄关之光雕塑的高度约为39米.
22. 为做好青少年安全教育工作，某校开展了主题为“珍爱生命，牢记安全”的知识竞赛（共20题，每题5分，满分100分）．该校从学生成绩都不低于80分的八年级（1）班和（3）班中，各随机抽取了20名学生成绩进行整理，绘制了不完整的统计表、条形统计图及分析表．
【收集数据】
八年级（1）班20名学生成绩：
85，95，100，90，90，80，85，90，80，100，80，85，95，90，95，95，95，95，100，95．
八年级（3）班20名学生成绩：
90，80，100，95，90，85，85，100，85，95，85，90，90，95，90，90，95，90，95，95．
【描述数据】
八年级（1）班20名学生成绩统计表
【分析数据】
八年级（1）班和（3）班20名学生成绩分析表
【应用数据】
根据以上信息，回答下列问题．
（1）请补全条形统计图：
（2）填空：______，______；
（3）你认为哪个班级的成绩更好一些？请说明理由；
（4）从上面5名得100分的学生中，随机抽取2名学生参加市级知识竞赛．请用列表法或画树状图法求所抽取的2名学生恰好在同一个班级的概率．
【答案】（1）答案见解析
（2）91，92.5 （3）八年级（1）班成绩较好，理由见解析
（4）
【解析】
【分析】（1）由八年级（3）班20名学生成绩统计可得90分学生有7人，95分学生有6人，补全条形统即可.
（2）由八年级（1）班20名学生成绩统计可得，，根据平均数和中位数的定义进行计算即可.
（3）从平均数，中位数和众数综合分析得八年级（1）班成绩较好.
（4）设八年级（1）班的三名100分的学生用A、B、C表示，八年级（3）班的两名100分的学生用X、Y表示，用列表法表示出所有可能结果，再从中找出2名学生恰好在同一个班级的结果数，再根据概率的计算公式进行计算即可．
【小问1详解】
由八年级（3）班20名学生成绩统计可得90分学生有7人，95分学生有6人，补全条形统计图如图所示：
小问2详解】
由八年级（1）班20名学生成绩统计可得，，
则，
一共20名学生，中位数应该为第10名与第11名的平均数，
．
【小问3详解】
八年级（1）班和八年级（3）班的平均成绩相同，而，
则八年级（1）班的中位数和众数都比八年级（3）班高，即八年级（1）班高分段人数较多，
所以八年级（1）班成绩较好．
【小问4详解】
设八年级（1）班的三名100分的学生用A、B、C表示．八年级（3）班的两名100分的学生用X、Y表示，
则随机抽两名学生的所有情况如下：
一共有20种情况，其中两名同学在同一个班级的有共8种，
所以所抽取的2名学生恰好在同一个班级的概率为．
23. 如图，内接于，D是上一点，．E是外一点，，连接．
（1）若，求的长；
（2）求证：是的切线．
【答案】（1）
（2）证明见解析
【解析】
【分析】（1）根据可得，然后证明，根据全等三角形的性质可得答案.
（2）连接，首先证明，再根据三角形内角和定理和圆周角定理求出，然后计算出即可．
【小问1详解】
由，得，又，，
则，
所以.
【小问2详解】
如图，连接，
由（1）得：，则，，
又，则，
而，于是，
又，则，
因此，而是半径，
所以是的切线．
24. 问题情境：“综合与实践”课上，老师提出如下问题：将图1中的矩形纸片沿对角线剪开，得到两个全等的三角形纸片，表示为和，其中．将和按图2所示方式摆放，其中点与点重合（标记为点）．当时，延长交于点．试判断四边形的形状，并说明理由．
（1）数学思考：谈你解答老师提出的问题；
（2）深入探究：老师将图2中的绕点逆时针方向旋转，使点落在内部，并让同学们提出新的问题．

①“善思小组”提出问题：如图3，当时，过点A作交的延长线于点与交于点．试猜想线段和的数量关系，并加以证明．请你解答此问题；

②“智慧小组”提出问题：如图4，当时，过点A作于点，若，求的长．请你思考此问题，直接写出结果．
【答案】（1）正方形，理由见解析
（2）①，证明见解析；②
【解析】
【分析】（1）先证明四边形是矩形，再由可得，从而得四边形是正方形；
（2）①由已知可得，再由等积方法，再结合已知即可证明结论；②设的交点为M，过M作于G，则易得，点G是的中点；利用三角函数知识可求得的长，进而求得的长，利用相似三角形的性质即可求得结果．
【小问1详解】
四边形为正方形．理由如下：
∵，
∴．
∵，
∴．
∴．
∵，
∴四边形为矩形．
∵，
∴．
∴矩形为正方形．
【小问2详解】
①，证明如下：
∵，
∴．
∵，
∴．
∵，即，
∴．
∵，
∴．
由（1）得，
∴．
②解：如图：设的交点为M，过M作于G，
∵，
∴，，
∴；
∵，
∴，
∴，
∵，
∴点G是的中点；
由勾股定理得，
∴；
∵，
∴，即；
∴；
∵，，
∴，
∴，
∴，即的长为．
25. 如图，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为，与y轴交于C点，点P是直线BC下方的抛物线上一动点．

（1）求这个二次函数的表达式；
（2）求出四边形的面积最大时的P点坐标和四边形的最大面积；
（3）在直线BC找一点Q，使得为等腰三角形，写出Q点坐标．
【答案】（1）；
（2），四边形的面积的最大值为；
（3）、、或．
【解析】
【分析】（1）把B、C两点的坐标代入二次函数即可求出b，c的值，故可得出二次函数的解析式.
（2）过点P作y轴的平行线与BC交于点Q，与OB交于点E，设，直线BC的解析式为，则Q点的坐标为，再根据即可得出结论.
（3）分当OC=QC时，当OC=QO时，当QC=QO时三种情况求解即可.
【小问1详解】
将B、C两点的坐标代入得，解得，
所以二次函数的表达式为：.
【小问2详解】
如图，过点P作y轴的平行线与BC交于点Q，与OB交于点F，

设，设直线BC的解析式为：，则，
解得，于是直线BC的解析式为，Q点的坐标为，
由，解得：，，即，
，
当时，四边形的面积最大，
此时P点的坐标为，四边形的面积的最大值为.
【小问3详解】
设点Q的坐标为，而，
则OC=3，，，
为等腰三角形分三种情况：
①当OC=QC时，，解得，
此时点Q的坐标为或，
②当时，，解得m=3或m=0（舍去），此时点Q的坐标为；
③当时，有，解得，此时点Q的坐标为，
所以Q点坐标为、、或.
活动课题
测量雄关之光雕塑的高度
工具
无人机
示意图
说明
如图②，用无人机在点处测得雕塑顶端处的仰角为，雕塑底端处的俯角为，无人机距离雕塑的水平距离为，雕塑垂直于地面，，，，在同一平面内
测量数据
米
分数
80
85
90
95
100
人数
3
3
a
b
3
统计量班级
平均数
中位数
众数
方差
八年级（1）班
95
41.5
八年级（3）班
91
90
26.5
（1）班 （3）班
A
B
C
X
Y
A
AB
AC
AX
AY
B
BA
BC
BX
BY
C
CA
CB
CX
CY
X
XA
XB
XC
XY
Y
YA
YB
YC
YX