高考数学科学创新复习方案提升版第23讲同角三角函数的基本关系与诱导公式学案（Word版附解析）

这是一份高考数学科学创新复习方案提升版第23讲同角三角函数的基本关系与诱导公式学案（Word版附解析），共18页。

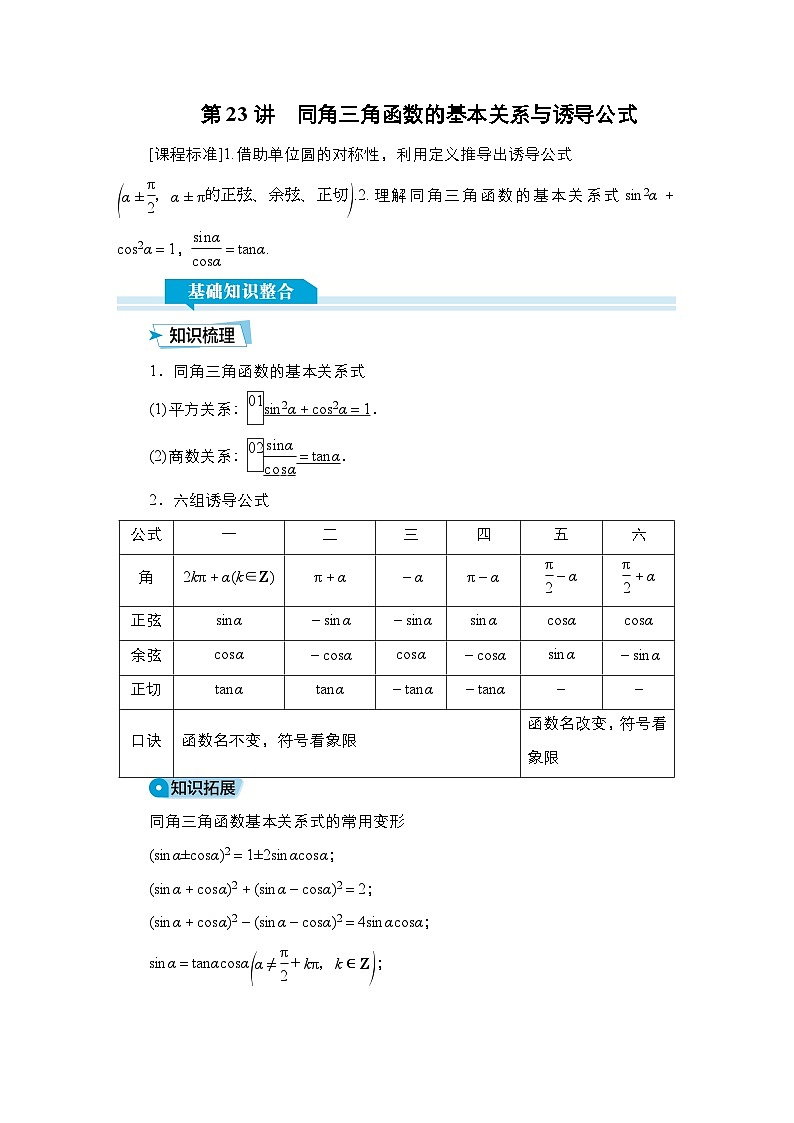
eq \b\lc\(\rc\)(\a\vs4\al\c1(α±\f(π,2)，α±π的正弦、余弦、正切)).2.理解同角三角函数的基本关系式sin2α＋cs2α＝1，eq \f(sinα,csα)＝tanα.
1．同角三角函数的基本关系式
(1)平方关系：eq \x(\s\up1(01))sin2α＋cs2α＝1．
(2)商数关系：eq \x(\s\up1(02))eq \f(sinα,csα)＝tanα．
2．六组诱导公式
同角三角函数基本关系式的常用变形
(sinα±csα)2＝1±2sinαcsα；
(sinα＋csα)2＋(sinα－csα)2＝2；
(sinα＋csα)2－(sinα－csα)2＝4sinαcsα；
sinα＝tanαcsαeq \b\lc\(\rc\)(\a\vs4\al\c1(α≠\f(π,2)＋kπ，k∈Z))；
sin2α＝eq \f(sin2α,sin2α＋cs2α)＝eq \f(tan2α,tan2α＋1)eq \b\lc\(\rc\)(\a\vs4\al\c1(α≠\f(π,2)＋kπ，k∈Z))；
cs2α＝eq \f(cs2α,sin2α＋cs2α)＝eq \f(1,tan2α＋1)eq \b\lc\(\rc\)(\a\vs4\al\c1(α≠\f(π,2)＋kπ，k∈Z)).
1．(人教B必修第三册7.2.3练习A T1(2)改编)若csα＝eq \f(1,3)，α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，0))，则tanα＝( )
A．－eq \f(\r(2),4) B.eq \f(\r(2),4)
C．－2eq \r(2) D．2eq \r(2)
答案 C
解析 由已知得sinα＝－eq \r(1－cs2α)＝－eq \r(1－\f(1,9))＝－eq \f(2\r(2),3)，所以tanα＝eq \f(sinα,csα)＝－2eq \r(2).故选C.
2．已知cs31°＝a，则sin239°tan149°的值为( )
A.eq \f(1－a2,a) B.eq \r(1－a2)
C.eq \f(a2－1,a) D．－eq \r(1－a2)
答案 B
解析 sin239°tan149°＝sin(270°－31°)tan(180°－31°)＝－cs31°·(－tan31°)＝sin31°＝eq \r(1－a2).
3．(人教B必修第三册第七章复习题A组T6改编)已知tanθ＝2，则eq \f(3sinα＋2csα,4sinα－3csα)＝________．
答案 eq \f(8,5)
解析 ∵tanθ＝2，∴原式＝eq \f(3tanα＋2,4tanα－3)＝eq \f(3×2＋2,4×2－3)＝eq \f(8,5).
4．(人教A必修第一册习题5.2 T12改编)已知α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，tanα＝2，则csα＝________．
答案 eq \f(\r(5),5)
解析 ∵α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，∴sinα＞0，csα＞0，∵tanα＝2＝eq \f(sinα,csα)，sin2α＋cs2α＝1，∴csα＝eq \f(\r(5),5).
5．(人教A必修第一册5.3例4改编)化简eq \f(cs\b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,2))),sin\b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋α)))·sin(α－π)cs(2π－α)的结果为________．
答案 －sin2α
解析 原式＝eq \f(sinα,csα)(－sinα)csα＝－sin2α.
多角度探究突破
角度 常规问题
例1 (1)已知角α的顶点为坐标原点，始边与x轴的非负半轴重合，终边上一点A(2sinα，3)(sinα≠0)，则csα＝( )
A.eq \f(1,2) B．－eq \f(1,2)
C.eq \f(\r(3),2) D．－eq \f(\r(3),2)
答案 A
解析 由三角函数定义，得tanα＝eq \f(3,2sinα)，所以eq \f(sinα,csα)＝eq \f(3,2sinα)，则2(1－cs2α)＝3csα，所以(2csα－1)(csα＋2)＝0，则csα＝eq \f(1,2).
(2)(2023·全国乙卷)若θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，tanθ＝eq \f(1,2)，则sinθ－csθ＝________．
答案 －eq \f(\r(5),5)
解析 因为θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，则sinθ>0，csθ>0，又因为tanθ＝eq \f(sinθ,csθ)＝eq \f(1,2)，则csθ＝2sinθ，且cs2θ＋sin2θ＝4sin2θ＋sin2θ＝5sin2θ＝1，解得sinθ＝eq \f(\r(5),5)或sinθ＝－eq \f(\r(5),5)(舍去)，所以sinθ－csθ＝sinθ－2sinθ＝－sinθ＝－eq \f(\r(5),5).
利用同角三角函数的基本关系式求值的三个基本题型
1.(2023·长郡十八校联盟联考)已知第二象限角α的终边上有两点A(－1，a)，B(b，2)，且csα＋3sinα＝0，则b－3a＝( )
A．－7 B．－5
C．5 D．7
答案 A
解析 因为csα＋3sinα＝0，所以3sinα＝－csα，所以tanα＝－eq \f(1,3)，又因为tanα＝eq \f(a,－1)＝eq \f(2,b)，所以a＝eq \f(1,3)，b＝－6，所以b－3a＝－7.故选A.
2．(2024·东莞模拟)已知2sin2θ－3sinθ－2＝0，θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，则csθ的值为( )
A.eq \f(\r(3),3) B.eq \f(\r(3),2) C.eq \f(\r(2),2) D.eq \f(1,2)
答案 B
解析 因为θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，则sinθ∈(－1，1)，csθ>0，因为2sin2θ－3sinθ－2＝(2sinθ＋1)·(sinθ－2)＝0，则sinθ＝－eq \f(1,2)，因此csθ＝eq \r(1－sin2θ)＝eq \f(\r(3),2).故选B.
角度 “1”的变换
例2 (2021·新高考Ⅰ卷)若tanθ＝－2，则eq \f(sinθ（1＋sin2θ）,sinθ＋csθ)＝( )
A．－eq \f(6,5) B．－eq \f(2,5)
C.eq \f(2,5) D.eq \f(6,5)
答案 C
解析 解法一：因为tanθ＝－2，所以eq \f(sinθ（1＋sin2θ）,sinθ＋csθ)＝eq \f(sinθ（sinθ＋csθ）2,sinθ＋csθ)＝sinθ(sinθ＋csθ)＝eq \f(sin2θ＋sinθcsθ,sin2θ＋cs2θ)＝eq \f(tan2θ＋tanθ,1＋tan2θ)＝eq \f(4－2,1＋4)＝eq \f(2,5).故选C.
解法二：eq \f(sinθ（1＋sin2θ）,sinθ＋csθ)＝eq \f(sinθ（sin2θ＋2sinθcsθ＋cs2θ）,sinθ＋csθ)＝sinθ(sinθ＋csθ)＝cs2θ(tan2θ＋tanθ)．由tanθ＝eq \f(sinθ,csθ)＝－2，sin2θ＋cs2θ＝1，解得cs2θ＝eq \f(1,5).所以eq \f(sinθ（1＋sin2θ）,sinθ＋csθ)＝cs2θ(tan2θ＋tanθ)＝eq \f(1,5)×(4－2)＝eq \f(2,5).故选C.
对于含有sin2α，cs2α，sinαcsα的三角函数求值问题，一般可以考虑添加分母1，再将1用“sin2α＋cs2α”代替，然后用分子分母同除以角的余弦的平方的方式将其转化为关于tanα的式子，从而求解．
(2023·海口模拟)已知角α的顶点为坐标原点，始边为x轴的非负半轴，终边上有一点P(1，2)，则eq \f(sin2α,1－3sinαcsα)＝________．
答案 －4
解析 因为角α的终边上有一点P(1，2)，所以tanα＝2.所以eq \f(sin2α,1－3sinαcsα)＝eq \f(sin2α,sin2α＋cs2α－3sinαcsα)＝eq \f(tan2α,tan2α＋1－3tanα)＝eq \f(22,22＋1－3×2)＝－4.
角度 sinx＋csx，sinx－csx，sinxcsx之间的关系
例3 (2023·济南模拟)已知α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，且sinα＋csα＝eq \f(\r(5),5)，则tanα的值为________．
答案 －eq \f(1,2)
解析 ∵sinα＋csα＝eq \f(\r(5),5)，∴sin2α＋cs2α＋2sinαcsα＝eq \f(1,5)，∴sinαcsα＝－eq \f(2,5)＜0，∴sin2α＋cs2α－2sinαcsα＝eq \f(9,5)＝(sinα－csα)2，又α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，∴sinα＜0，csα＞0，∴csα－sinα＝eq \f(3\r(5),5)，∴sinα＝－eq \f(\r(5),5)，csα＝eq \f(2\r(5),5)，∴tanα＝－eq \f(1,2).
(1)已知asinx＋bcsx＝c可与sin2x＋cs2x＝1联立，求得sinx，csx.
(2)sinx＋csx，sinx－csx，sinxcsx之间的关系为
(sinx＋csx)2＝1＋2sinxcsx，
(sinx－csx)2＝1－2sinxcsx，
(sinx＋csx)2＋(sinx－csx)2＝2.
因此，已知上述三个代数式中的任意一个代数式的值，便可求其余两个代数式的值．
(2024·青岛调研)若sinθ＋csθ＝eq \f(2\r(3),3)，则sin4θ＋cs4θ＝( )
A.eq \f(5,6) B.eq \f(17,18)
C.eq \f(8,9) D.eq \f(2,3)
答案 B
解析 由sinθ＋csθ＝eq \f(2\r(3),3)，平方得1＋2sinθcsθ＝eq \f(4,3)，∴sinθcsθ＝eq \f(1,6)，∴sin4θ＋cs4θ＝(sin2θ＋cs2θ)2－2sin2θcs2θ＝1－2×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,6)))eq \s\up12(2)＝eq \f(17,18).故选B.
例4 (1)(2023·北京市八一中学模拟)若角α的终边在第三象限，则下列三角函数值中小于零的是( )
A．sin(π＋α) B．cs(π－α)
C．cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α)) D．sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))
答案 D
解析 因为角α的终边在第三象限，所以sinα<0，csα<0.对于A，sin(π＋α)＝－sinα>0；对于B，cs(π－α)＝－csα>0；对于C，cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α))＝－sinα>0；对于D，sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))＝csα<0.故选D.
(2)化简：eq \f(tan（π＋α）cs（2π＋α）sin\b\lc\(\rc\)(\a\vs4\al\c1(α－\f(3π,2))),cs（－α－3π）sin（－3π－α）)＝________．
答案 －1
解析 原式＝eq \f(tanαcsαsin\b\lc\[\rc\](\a\vs4\al\c1(－2π＋\b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,2))))),cs（3π＋α）[－sin（3π＋α）])
＝eq \f(tanαcsαsin\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋α)),－csαsinα)＝eq \f(tanαcsαcsα,－csαsinα)
＝－eq \f(tanαcsα,sinα)＝－eq \f(sinα,csα)·eq \f(csα,sinα)＝－1.
(3)已知cs(75°＋α)＝eq \f(5,13)，α是第三象限角，则sin(195°－α)＋cs(α－15°)的值为________．
答案 －eq \f(17,13)
解析 因为cs(75°＋α)＝eq \f(5,13)>0，α是第三象限角，所以75°＋α是第四象限角，sin(75°＋α)＝－eq \r(1－cs2（75°＋α）)＝－eq \f(12,13).所以sin(195°－α)＋cs(α－15°)＝sin[180°＋(15°－α)]＋cs(15°－α)＝－sin(15°－α)＋cs(15°－α)＝－sin[90°－(75°＋α)]＋cs[90°－(75°＋α)]＝－cs(75°＋α)＋sin(75°＋α)＝－eq \f(5,13)－eq \f(12,13)＝－eq \f(17,13).
利用诱导公式化简求值的基本步骤
提醒：用诱导公式求值时，要善于观察所给角之间的关系，利用整体代换的思想简化解题过程．常见的互余关系有eq \f(π,3)－α与eq \f(π,6)＋α，eq \f(π,3)＋α与eq \f(π,6)－α，eq \f(π,4)＋α与eq \f(π,4)－α等，常见的互补关系有eq \f(π,6)－θ与eq \f(5π,6)＋θ，eq \f(π,3)＋θ与eq \f(2π,3)－θ，eq \f(π,4)＋θ与eq \f(3π,4)－θ等．
1.(2024·江西宜春中学诊断)若α为锐角，且cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(π,6)))＝eq \f(1,3)，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,3)))的值为( )
A.eq \f(2\r(2),3) B.eq \f(\r(2),3)
C.eq \f(\r(2),6) D.eq \f(5\r(2),6)
答案 A
解析 ∵0<α2．(2023·咸阳模拟)已知角α终边上一点P(sin1180°，cs1180°)，那么cs(3α＋60°)＝( )
A．0 B.eq \f(1,2)
C．1 D.eq \f(\r(3),2)
答案 D
解析 ∵|OP|＝eq \r(sin21180°＋cs21180°)＝1，∴sinα＝cs1180°＝cs(100°＋3×360°)＝cs100°＝－sin10°＝sin(－10°)，csα＝sin1180°＝sin(100°＋3×360°)＝sin100°＝cs10°＝cs(－10°)，∴α＝－10°＋k·360°(k∈Z)，cs(3α＋60°)＝cs(－30°＋3k·360°＋60°)＝cs30°＝eq \f(\r(3),2).故选D.
例5 (1)(2023·南京二模)利用诱导公式可以将任意角的三角函数值转化为0°～90°之间角的三角函数值，而这个范围内的三角函数值又可以通过查三角函数表得到．如表为部分锐角的正弦值，则tan1600°的值为(小数点后保留两位有效数字)( )
A.－0.42 B．－0.36
C．0.36 D．0.42
答案 B
解析 tan1600°＝tan(4×360°＋160°)＝tan160°＝－tan20°＝－eq \f(sin20°,cs20°)＝－eq \f(sin20°,sin70°)＝－eq \f(0.3420,0.9397)≈－0.36.故选B.
(2)(2023·聊城模拟)已知角α为锐角，且2tan(π－α)－3cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋β))＋5＝0，tan(π＋α)＋6sin(π＋β)－1＝0，则sinα＝( )
A.eq \f(3\r(5),5) B.eq \f(3\r(7),7)
C.eq \f(3\r(10),10) D.eq \f(1,3)
答案 C
解析 由已知得eq \b\lc\{(\a\vs4\al\c1(3sinβ－2tanα＋5＝0，,tanα－6sinβ－1＝0，))消去sinβ，得tanα＝3，所以sinα＝3csα，代入sin2α＋cs2α＝1，化简得sin2α＝eq \f(9,10)，因为α为锐角，所以sinα＝eq \f(3\r(10),10).
(1)利用同角三角函数的基本关系式和诱导公式求值或化简时，关键是寻求条件、结论间的联系，灵活使用公式进行变形．
(2)注意角的范围对三角函数符号的影响．
1.(2023·吉安模拟)已知cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)＋α))＝－eq \f(3,5)，且α是第四象限角，则cs(－3π＋α)的值为( )
A.eq \f(4,5) B．－eq \f(4,5)
C．±eq \f(4,5) D.eq \f(3,5)
答案 B
解析 ∵cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)＋α))＝－eq \f(3,5)，∴sinα＝－eq \f(3,5).∵α是第四象限角，∴cs(－3π＋α)＝－csα＝－eq \r(1－sin2α)＝－eq \f(4,5).故选B.
2．(2023·黄山模拟)已知taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)－x))＝eq \f(1,csx)，则sinx＝( )
A.eq \f(\r(3)－1,2) B.eq \f(\r(5)－1,2)
C.eq \f(1－\r(5),2) D.eq \f(－1±\r(5),2)
答案 B
解析 由taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)－x))＝eq \f(1,csx)，可得eq \f(csx,sinx)＝eq \f(1,csx)，即cs2x－sinx＝0，即sin2x＋sinx－1＝0，解得sinx＝eq \f(－1＋\r(5),2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(－1－\r(5),2)舍去)).故选B.
课时作业
一、单项选择题
1．(2024·衡阳月考)若角α的终边在第三象限，则eq \f(csα,\r(1－sin2α))＋eq \f(2sinα,\r(1－cs2α))的值为( )
A．3 B．－3
C．1 D．－1
答案 B
解析 因为角α的终边在第三象限，所以sinα<0，csα<0，所以原式＝eq \f(csα,－csα)＋eq \f(2sinα,－sinα)＝－3.
2．设sin25°＝a，则sin65°cs115°tan205°＝( )
A.eq \f(a2,\r(1－a2)) B．－eq \f(a2,\r(1－a2))
C．－a2 D．a2
答案 C
解析 因为sin65°＝cs25°，cs115°＝cs(90°＋25°)＝－sin25°，tan205°＝tan(180°＋25°)＝tan25°＝eq \f(sin25°,cs25°)，所以sin65°cs115°tan205°＝－sin225°＝－a2.
3．(2023·湖北四校联考)已知角α是第二象限角，且满足sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋α))＋3cs(α－π)＝1，则tan(π＋α)＝( )
A.eq \r(3) B．－eq \r(3)
C．－eq \f(\r(3),3) D．－1
答案 B
解析 由sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,2)＋α))＋3cs(α－π)＝1，得csα－3csα＝1，∴csα＝－eq \f(1,2)，∵角α是第二象限角，∴sinα＝eq \f(\r(3),2)，∴tan(π＋α)＝tanα＝eq \f(sinα,csα)＝－eq \r(3).
4．(2024·泰安质检)已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,12)))＝eq \f(1,3)，则cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(17π,12)))的值为( )
A.eq \f(1,3) B.eq \f(2\r(2),3)
C．－eq \f(1,3) D．－eq \f(2\r(2),3)
答案 A
解析 cseq \b\lc\(\rc\)(\a\vs4\al\c1(α＋\f(17π,12)))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,12)＋\f(3π,2)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(α－\f(π,12)))＝eq \f(1,3).
5．已知函数f(x)＝asin(πx＋α)＋bcs(πx＋β)，且f(3)＝3，则f(2024)的值为( )
A．－1 B．1
C．3 D．－3
答案 D
解析 ∵函数f(x)＝asin(πx＋α)＋bcs(πx＋β)，∴f(3)＝asin(3π＋α)＋bcs(3π＋β)＝－(asinα＋bcsβ)＝3，∴asinα＋bcsβ＝－3.∴f(2024)＝asin(2024π＋α)＋bcs(2024π＋β)＝asinα＋bcsβ＝－3.故选D.
6．(2023·辽宁校考一模)已知角α的终边上一点的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(sin\f(4π,5)，cs\f(4π,5)))，则α的最小正值为( )
A.eq \f(π,5) B.eq \f(3π,10)
C.eq \f(4π,5) D.eq \f(17π,10)
答案 D
解析 因为eq \f(4π,5)＝eq \f(π,2)－eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))，所以sineq \f(4π,5)＝sineq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)－\b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))，而cseq \f(4π,5)＝cseq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)－\b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))，所以角α终边上的点的坐标可写为eq \b\lc\(\rc\)(\a\vs4\al\c1(cs\b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))，sin\b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))))，所以α＝－eq \f(3π,10)＋2kπ，k∈Z，因此α的最小正值为－eq \f(3π,10)＋2π＝eq \f(17π,10).故选D.
7．(2023·益阳模拟)若eq \f(sinα＋csα,sinα－csα)＝eq \f(1,2)，则sin2α－sinαcsα－3cs2α＝( )
A.eq \f(1,10) B.eq \f(3,10)
C.eq \f(9,10) D．－eq \f(3,2)
答案 C
解析 由eq \f(sinα＋csα,sinα－csα)＝eq \f(1,2)，得eq \f(tanα＋1,tanα－1)＝eq \f(1,2)，即tanα＝－3，∴sin2α－sinαcsα－3cs2α＝eq \f(sin2α－sinαcsα－3cs2α,sin2α＋cs2α)＝eq \f(tan2α－tanα－3,tan2α＋1)＝eq \f(9,10).故选C.
8．(2024·青岛模拟)田忌赛马是中国古代对策论与运筹思想运用的著名范例．故事中齐将田忌与齐王赛马，孙膑献策以下马对齐王上马，以上马对齐王中马，以中马对齐王下马，结果田忌一负两胜，从而获胜．在比大小游戏中(大者为胜)，已知我方的三个数为a＝csθ，b＝sinθ＋csθ，c＝csθ－sinθ，对方的三个数以及排序如表：
若0<θA．a，b，c B．b，c，a
C．c，a，b D．c，b，a
答案 D
解析 因为当0<θ0，csθ>0，tanθ>0，sinθ－tanθ＝eq \f(sinθ（csθ－1）,csθ)<0，所以sinθ1，所以b＝sinθ＋csθ>1>tanθ，a＝csθ>sinθ，c＝csθ－sinθ<2，故类比“田忌赛马”，我方必胜的排序是c，b，a.故选D.
二、多项选择题
9．在△ABC中，下列结论正确的是( )
A．sin(A＋B)＝sinCB．sineq \f(B＋C,2)＝cseq \f(A,2)
C．tan(A＋B)＝－tanCeq \b\lc\(\rc\)(\a\vs4\al\c1(C≠\f(π,2)))D．cs(A＋B)＝csC
答案 ABC
解析 在△ABC中，有A＋B＋C＝π，则sin(A＋B)＝sin(π－C)＝sinC；sineq \f(B＋C,2)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－\f(A,2)))＝cseq \f(A,2)；tan(A＋B)＝tan(π－C)＝－tanCeq \b\lc\(\rc\)(\a\vs4\al\c1(C≠\f(π,2)))；cs(A＋B)＝cs(π－C)＝－csC.
10．(2024·淄博调研)已知θ∈(0，π)，sinθ＋csθ＝eq \f(1,5)，则下列结论正确的是( )
A．θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π)) B．csθ＝－eq \f(3,5)
C．tanθ＝－eq \f(3,4) D．sinθ－csθ＝eq \f(7,5)
答案 ABD
解析 因为sinθ＋csθ＝eq \f(1,5)，所以1＋2sinθcsθ＝eq \f(1,25)，所以2sinθcsθ＝－eq \f(24,25)<0，又θ∈(0，π)，所以θ∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))，A正确；进而可得sinθ>csθ，因为(sinθ－csθ)2＝1－2sinθcsθ＝eq \f(49,25)，所以sinθ－csθ＝eq \f(7,5)，D正确；由eq \b\lc\{(\a\vs4\al\c1(sinθ＋csθ＝\f(1,5)，,sinθ－csθ＝\f(7,5)，))解得sinθ＝eq \f(4,5)，csθ＝－eq \f(3,5)，进而得tanθ＝－eq \f(4,3)，故B正确，C错误．故选ABD.
11．(2023·宜昌高三模拟)定义：角θ与φ都是任意角，若满足θ＋φ＝eq \f(π,2)，则称θ与φ“广义互余”．已知sin(π＋α)＝－eq \f(1,4)，下列角β中，可能与角α“广义互余”的是( )
A．sinβ＝eq \f(\r(15),4) B．cs(π＋β)＝eq \f(1,4)
C．tanβ＝eq \r(15) D．tanβ＝eq \f(\r(15),5)
答案 AC
解析 ∵sin(π＋α)＝－sinα＝－eq \f(1,4)，∴sinα＝eq \f(1,4)，若α＋β＝eq \f(π,2)，则β＝eq \f(π,2)－α.sinβ＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))＝csα＝±eq \f(\r(15),4)，故A符合条件；cs(π＋β)＝－cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－α))＝－sinα＝－eq \f(1,4)，故B不符合条件；tanβ＝eq \r(15)，即sinβ＝eq \r(15)csβ，又sin2β＋cs2β＝1，∴sinβ＝±eq \f(\r(15),4)，故C符合条件；tanβ＝eq \f(\r(15),5)，即sinβ＝eq \f(\r(15),5)csβ，又sin2β＋cs2β＝1，∴sinβ＝±eq \f(\r(6),4)，故D不符合条件．故选AC.
三、填空题
12．(2023·西安调研)sin(－570°)＋cs(－2640°)＋tan1665°＝________．
答案 1
解析 原式＝sin(－570°＋720°)＋cs(－2640°＋2880°)＋tan(1665°－1620°)＝sin150°＋cs240°＋tan45°＝sin30°－cs60°＋1＝eq \f(1,2)－eq \f(1,2)＋1＝1.
13．已知角α的顶点为坐标原点，始边与x轴的非负半轴重合，终边过点P(sin138°，cs138°)，则tan(α＋18°)＝________．
答案 －eq \f(\r(3),3)
解析 因为cs138°<0，sin138°>0，所以点P在第四象限，即α为第四象限角，由三角函数定义得tanα＝eq \f(cs138°,sin138°)＝eq \f(cs（90°＋48°）,sin（90°＋48°）)＝eq \f(－sin48°,cs48°)＝eq \f(sin（－48°）,cs（－48°）)＝tan(－48°)，所以α＝－48°＋k·360°，k∈Z，所以tan(α＋18°)＝tan(－48°＋k·360°＋18°)＝tan(－30°)＝－eq \f(\r(3),3).
14．(2023·浙江名校协作体检测)已知sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)－α))cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(7π,2)＋α))＝eq \f(12,25)，且0<α答案 eq \f(3,5) eq \f(4,5)
解析 sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)－α))cseq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(7π,2)＋α))＝－csα(－sinα)＝sinαcsα＝eq \f(12,25).∵0<α四、解答题
15．已知eq \f(tanα,tanα－1)＝－1，求下列各式的值．
(1)eq \f(sinα－3csα,sinα＋csα)；
(2)sin2α＋sinαcsα＋2.
解 由已知得tanα＝eq \f(1,2).
(1)eq \f(sinα－3csα,sinα＋csα)＝eq \f(tanα－3,tanα＋1)＝－eq \f(5,3).
(2)sin2α＋sinαcsα＋2＝eq \f(sin2α＋sinαcsα,sin2α＋cs2α)＋2＝eq \f(tan2α＋tanα,tan2α＋1)＋2＝eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))\s\up12(2)＋\f(1,2),\b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))\s\up12(2)＋1)＋2＝eq \f(13,5).
16．(2023·郴州质检)已知－eq \f(π,2)<α<0，且函数f(α)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)＋α))－sinα·eq \r(\f(1＋csα,1－csα))－1.
(1)化简f(α)；
(2)若f(α)＝eq \f(1,5)，求sinαcsα和sinα－csα的值．
解 (1)∵－eq \f(π,2)<α<0，∴sinα<0，
∴f(α)＝sinα－sinα·eq \r(\f(（1＋csα）2,1－cs2α))－1＝sinα＋sinα·eq \f(1＋csα,sinα)－1＝sinα＋csα.
(2)解法一：由f(α)＝sinα＋csα＝eq \f(1,5)，平方可得sin2α＋2sinαcsα＋cs2α＝eq \f(1,25)，
即2sinαcsα＝－eq \f(24,25)，∴sinαcsα＝－eq \f(12,25).
又－eq \f(π,2)<α<0，∴sinα<0，csα>0，
∴sinα－csα<0.
∵(sinα－csα)2＝1－2sinαcsα＝eq \f(49,25)，
∴sinα－csα＝－eq \f(7,5).
解法二：联立方程eq \b\lc\{(\a\vs4\al\c1(sinα＋csα＝\f(1,5)，,sin2α＋cs2α＝1，))
解得eq \b\lc\{(\a\vs4\al\c1(sinα＝－\f(3,5)，,csα＝\f(4,5)))或eq \b\lc\{(\a\vs4\al\c1(sinα＝\f(4,5)，,csα＝－\f(3,5).))
∵－eq \f(π,2)<α<0，∴eq \b\lc\{(\a\vs4\al\c1(sinα＝－\f(3,5)，,csα＝\f(4,5)，))
∴sinαcsα＝－eq \f(12,25)，sinα－csα＝－eq \f(7,5).
17．是否存在α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，β∈(0，π)，使等式sin(3π－α)＝eq \r(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－β))，eq \r(3)cs(－α)＝－eq \r(2)cs(π＋β)同时成立？若存在，求出α，β的值；若不存在，说明理由．
解 存在．
由sin(3π－α)＝eq \r(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－β))得
sinα＝eq \r(2)sinβ，①
由eq \r(3)cs(－α)＝－eq \r(2)cs(π＋β)得
eq \r(3)csα＝eq \r(2)csβ，②
∴sin2α＋3cs2α＝2(sin2β＋cs2β)＝2，
∴1＋2cs2α＝2，∴cs2α＝eq \f(1,2)，
又α∈eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))，∴csα＝eq \f(\r(2),2)，
从而α＝eq \f(π,4)或－eq \f(π,4)，
当α＝eq \f(π,4)时，由①知sinβ＝eq \f(1,2)，
由②知csβ＝eq \f(\r(3),2)，
又β∈(0，π)，∴β＝eq \f(π,6)，
当α＝－eq \f(π,4)时，由①知sinβ＝－eq \f(1,2)，
与β∈(0，π)矛盾，舍去．
∴存在α＝eq \f(π,4)，β＝eq \f(π,6)，符合题意．公式
一
二
三
四
五
六
角
2kπ＋α(k∈Z)
π＋α
－α
π－α
eq \f(π,2)－α
eq \f(π,2)＋α
正弦
sinα
－sinα
－sinα
sinα
csα
csα
余弦
csα
－csα
csα
－csα
sinα
－sinα
正切
tanα
tanα
－tanα
－tanα
－
－
口诀
函数名不变，符号看象限
函数名改变，符号看象限
考向一 同角三角函数的基本关系
考向二 诱导公式的应用
考向三 诱导公式与同角三角函数基本关系式的综合应用
α
10°
20°
30°
40°
sinα
0.1736
0.3420
0.5000
0.6428
α
50°
60°
70°
80°
sinα
0.7660
0.8660
0.9397
0.9848
第一局
第二局
第三局
2
tanθ
sinθ