高考数学科学创新复习方案提升版第26讲三角函数的图象与性质学案（Word版附解析）

这是一份高考数学科学创新复习方案提升版第26讲三角函数的图象与性质学案（Word版附解析），共25页。


1．用五点法作正弦函数和余弦函数的简图
(1)在正弦函数y＝sinx，x∈[0，2π]的图象上，五个关键点是：(0，0)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，1))，(π，0)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，－1))，(2π，0)．
(2)在余弦函数y＝csx，x∈[0，2π]的图象上，五个关键点是：(0，1)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，0))，(π，－1)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，0))，(2π，1)．
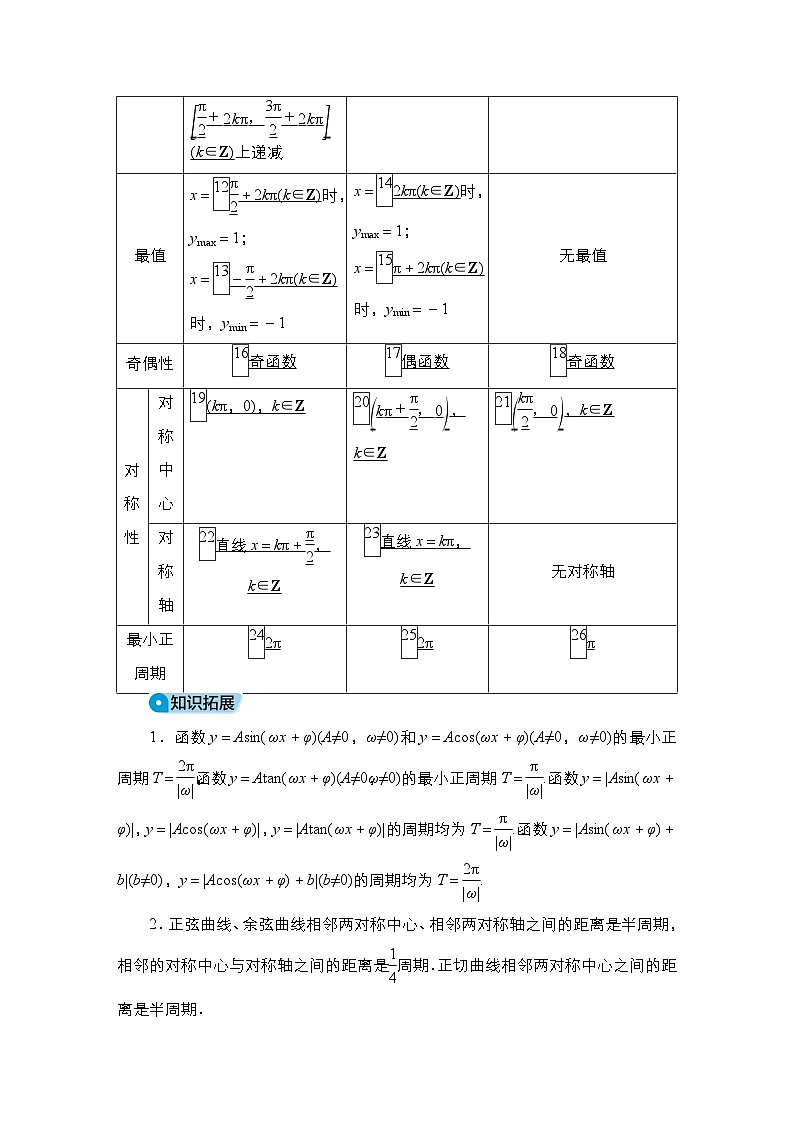
2．正弦、余弦、正切函数的图象与性质
1．函数y＝Asin(ωx＋φ)(A≠0，ω≠0)和y＝Acs(ωx＋φ)(A≠0，ω≠0)的最小正周期T＝eq \f(2π,|ω|)，函数y＝Atan(ωx＋φ)(A≠0，ω≠0)的最小正周期T＝eq \f(π,|ω|).函数y＝|Asin(ωx＋φ)|，y＝|Acs(ωx＋φ)|，y＝|Atan(ωx＋φ)|的周期均为T＝eq \f(π,|ω|).函数y＝|Asin(ωx＋φ)＋b|(b≠0)，y＝|Acs(ωx＋φ)＋b|(b≠0)的周期均为T＝eq \f(2π,|ω|).
2．正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期，相邻的对称中心与对称轴之间的距离是eq \f(1,4)周期．正切曲线相邻两对称中心之间的距离是半周期．
3．若f(x)＝Asin(ωx＋φ)(A≠0，ω≠0)，则
(1)f(x)为偶函数的充要条件是φ＝eq \f(π,2)＋kπ(k∈Z)；
(2)f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．
1．函数y＝1－sinx，x∈[0，2π]的大致图象是( )
答案 B
解析 当x＝0时，y＝1；当x＝eq \f(π,2)时，y＝0；当x＝π时，y＝1；当x＝eq \f(3π,2)时，y＝2；当x＝2π时，y＝1.结合正弦函数的图象可知B正确．故选B.
2．下列函数中，最小正周期为2π的奇函数为( )
A．y＝sineq \f(x,2)cseq \f(x,2) B．y＝sin2x
C．y＝tan2x D．y＝sin2x＋cs2x
答案 A
解析 y＝sin2x为偶函数；y＝tan2x的最小正周期为eq \f(π,2)；y＝sin2x＋cs2x为非奇非偶函数，故B，C，D都不正确．故选A.
3．(2021·新高考Ⅰ卷)下列区间中，函数f(x)＝7sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6)))单调递增的区间是( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2))) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，π))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(π，\f(3π,2))) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，2π))
答案 A
解析 令－eq \f(π,2)＋2kπ≤x－eq \f(π,6)≤eq \f(π,2)＋2kπ，k∈Z，得－eq \f(π,3)＋2kπ≤x≤eq \f(2π,3)＋2kπ，k∈Z.取k＝0，则－eq \f(π,3)≤x≤eq \f(2π,3).因为eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(2π,3)))，所以区间eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))是函数f(x)的单调递增区间．故选A.
4．(人教B必修第三册第七章复习题A组T14改编)函数f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象的对称轴方程为________，对称中心的坐标为________．
答案 x＝－eq \f(π,6)＋eq \f(kπ,2)(k∈Z) eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)＋\f(kπ,2)，0))(k∈Z)
解析 令2x＋eq \f(π,3)＝kπ(k∈Z)，解得对称轴方程为x＝－eq \f(π,6)＋eq \f(kπ,2)(k∈Z)；函数f(x)的对称中心的横坐标满足2x＋eq \f(π,3)＝kπ＋eq \f(π,2)(k∈Z)，解得x＝eq \f(π,12)＋eq \f(kπ,2)(k∈Z)，所以对称中心的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)＋\f(kπ,2)，0))(k∈Z)．
5．(人教A必修第一册习题5.4 T10改编)y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))在区间eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上的值域是________．
答案 eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(3,2)，3))
解析 当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))时，2x－eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(5π,6)))，sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，1))，故3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(3,2)，3))，即y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))在区间eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上的值域为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(3,2)，3)).
例1 (1)函数y＝2taneq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,6)))的定义域为________．
答案 eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(π,9)＋\f(kπ,3)，k∈Z))))
解析 由3x＋eq \f(π,6)≠kπ＋eq \f(π,2)，k∈Z，解得x≠eq \f(π,9)＋eq \f(kπ,3)，k∈Z，所以函数y＝2taneq \b\lc\(\rc\)(\a\vs4\al\c1(3x＋\f(π,6)))的定义域为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(π,9)＋\f(kπ,3)，k∈Z)))).
(2)函数y＝lg sin2x＋eq \r(9－x2)的定义域为________．
答案 eq \b\lc\[\rc\)(\a\vs4\al\c1(－3，－\f(π,2)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))
解析 由eq \b\lc\{(\a\vs4\al\c1(sin2x＞0，,9－x2≥0，))得eq \b\lc\{(\a\vs4\al\c1(kπ＜x＜kπ＋\f(π,2)，k∈Z，,－3≤x≤3，))∴－3≤x＜－eq \f(π,2)或0＜x＜eq \f(π,2).∴函数y＝lg sin2x＋eq \r(9－x2)的定义域为eq \b\lc\[\rc\)(\a\vs4\al\c1(－3，－\f(π,2)))∪eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2))).
(3)(2023·北京丰台区二模)若函数f(x)＝sinx－cs2x，则feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))＝________，f(x)的值域为________．
答案 0 eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(9,8)，2))
解析 feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))＝sineq \f(π,6)－cseq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(π,6)))＝eq \f(1,2)－eq \f(1,2)＝0.f(x)＝sinx－cs2x＝sinx－(1－2sin2x)＝2sin2x＋sinx－1，设t＝sinx∈[－1，1]，则y＝2t2＋t－1，t∈[－1，1]，当t∈eq \b\lc\[\rc\)(\a\vs4\al\c1(－1，－\f(1,4)))时，y＝2t2＋t－1单调递减，当t∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,4)，1))时，y＝2t2＋t－1单调递增，所以当t＝－eq \f(1,4)时，ymin＝－eq \f(9,8)；当t＝1时，ymax＝2.所以f(x)的值域为eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(9,8)，2)).
(4)函数y＝sinx－csx＋sinxcsx，x∈[0，π]的最大值与最小值的差为________．
答案 2
解析 令t＝sinx－csx，又x∈[0，π]，∴t＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))，t∈[－1，eq \r(2)]．由t＝sinx－csx，得t2＝1－2sinxcsx，即sinxcsx＝eq \f(1－t2,2).∴原函数变为y＝t＋eq \f(1－t2,2)，t∈[－1，eq \r(2)]，即y＝－eq \f(1,2)t2＋t＋eq \f(1,2).∴当t＝1时，ymax＝－eq \f(1,2)＋1＋eq \f(1,2)＝1；当t＝－1时，ymin＝－eq \f(1,2)－1＋eq \f(1,2)＝－1.故函数的最大值与最小值的差为2.
1．三角函数定义域的求法
(1)求三角函数的定义域常常归结为解三角不等式(或等式)．
(2)求三角函数的定义域经常借助三角函数的图象，有时也利用数轴．
(3)对于较为复杂的求三角函数的定义域问题，应先列出不等式(组)分别求解，然后利用数轴求交集．
2．求三角函数的值域(最值)的三种类型及解题思路
(1)形如y＝asinx＋bcsx＋c的三角函数化为y＝Asin(ωx＋φ)＋c的形式，再求值域(最值)．
(2)形如y＝asin2x＋bsinx＋c的三角函数，可先设sinx＝t，化为关于t的二次函数求值域(最值)．
(3)形如y＝asinxcsx＋b(sinx±csx)＋c的三角函数，可先设t＝sinx±csx，化为关于t的二次函数求值域(最值)．
1.(2023·新乡三模)已知函数f(x)＝4sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))＋1的定义域是[0，m]，值域为[－1，5]，则m的最大值是( )
A.eq \f(2π,3) B.eq \f(π,3)
C.eq \f(π,6) D.eq \f(5π,6)
答案 A
解析 ∵x∈[0，m]，∴2x－eq \f(π,6)∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，2m－\f(π,6))).∵f(x)的值域为[－1，5]，∴－eq \f(1,2)≤sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))≤1，∴eq \f(π,2)≤2m－eq \f(π,6)≤eq \f(7π,6)，解得eq \f(π,3)≤m≤eq \f(2π,3)，∴m的最大值为eq \f(2π,3).故选A.
2．函数y＝lg (sinx－csx)的定义域是________．
答案 eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(\f(π,4)＋2kπ解析 要使函数有意义，必须使sinx－csx>0.利用图象，在同一坐标系中画出[0，2π]上y＝sinx和y＝csx的图象，如图所示：
在[0，2π]内，满足sinx＝csx的x为eq \f(π,4)，eq \f(5π,4)，在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，\f(5π,4)))内sinx>csx，再结合正弦、余弦函数的周期是2π，所以定义域为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(\f(π,4)＋2kπ例2 (1)(2024·济南质检)已知函数f(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))，设a＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,7)))，b＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))，c＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))，则a，b，c的大小关系是( )
A．a>b>c B．a>c>b
C．c>a>b D．b>a>c
答案 A
解析 由2kπ≤x＋eq \f(π,6)≤2kπ＋π，k∈Z得2kπ－eq \f(π,6)≤x≤2kπ＋eq \f(5π,6)，k∈Z，所以f(x)＝2cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))的单调递减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,6)，2kπ＋\f(5π,6)))(k∈Z)，所以f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))上单调递减，所以feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,7)))>feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))>feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))，即a>b>c.
(2)函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－2x))(x∈[0，π])的单调递增区间是( )
A.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,3))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,12)，\f(7π,12)))
C.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(5π,6))) D.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,6)，π))
答案 C
解析 y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)－2x))＝－2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))，由eq \f(π,2)＋2kπ≤2x－eq \f(π,6)≤eq \f(3π,2)＋2kπ，k∈Z，解得eq \f(π,3)＋kπ≤x≤eq \f(5π,6)＋kπ，k∈Z，即函数的单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)＋kπ，\f(5π,6)＋kπ))，k∈Z，∴当k＝0时，单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(5π,6))).
1．求三角函数单调区间的两种方法
(1)代换法：将比较复杂的三角函数解析式中含自变量的代数式(如ωx＋φ)整体当作一个角，利用基本三角函数(y＝sinx，y＝csx，y＝tanx)的单调性列不等式求解．
(2)图象法：画出三角函数的图象，利用图象求函数的单调区间．
提醒：要注意求函数y＝Asin(ωx＋φ)的单调区间时ω的符号，若ω<0，那么一定要先借助诱导公式将ω化为正数．同时切莫忘记考虑函数自身的定义域．
2．比较三角函数值大小的方法
先统一为同名的三角函数，然后利用诱导公式把角化为同一单调区间内的角，再利用函数的单调性比较．
1.(2024·山东新高考联合质量测评)已知f(x)＝cs(2x＋φ)，|φ|A．f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(5π,6)))上单调递增
B．f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(5π,6)))上单调递减
C．f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)，\f(π,6)))上单调递增
D．f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)，\f(π,6)))上单调递减
答案 C
解析 因为f(x)＝cs(2x＋φ)，|φ|2．(2024·德州开学考试)函数y＝|tanx|的单调递增区间为________，单调递减区间为________．
答案 eq \b\lc\[\rc\)(\a\vs4\al\c1(kπ，kπ＋\f(π,2)))，k∈Z eq \b\lc\(\rc\](\a\vs4\al\c1(kπ－\f(π,2)，kπ))，k∈Z
解析 作出函数y＝|tanx|的图象，如图．
观察图象可知，函数y＝|tanx|的单调递增区间为eq \b\lc\[\rc\)(\a\vs4\al\c1(kπ，kπ＋\f(π,2)))，k∈Z，单调递减区间为eq \b\lc\(\rc\](\a\vs4\al\c1(kπ－\f(π,2)，kπ))，k∈Z.
多角度探究突破
角度 三角函数的周期性
例3 (1)函数f(x)＝csx＋2cseq \f(1,2)x的一个周期为( )
A．π B．2π
C．3π D．4π
答案 D
解析 易知y＝csx，y1＝2cseq \f(1,2)x的最小正周期分别为2π，4π，则2π，4π的公倍数4π是f(x)的一个周期．故选D.
(2)(2023·南昌模拟)函数f(x)＝eq \f(1－cs4x,sin4x)的最小正周期是( )
A.eq \f(π,4) B.eq \f(π,2)
C．π D．2π
答案 B
解析 因为f(x)＝eq \f(1－cs4x,sin4x)＝eq \f(2sin22x,2sin2xcs2x)＝tan2x，所以最小正周期T＝eq \f(π,2).
(3)(2023·辽宁实验中学模拟)函数f(x)＝|sinx|＋|csx|的最小正周期和最小值分别为( )
A.eq \f(π,4)，1 B.eq \f(π,2)，eq \f(\r(2),2)
C.eq \f(π,2)，1 D．π，1
答案 C
解析 解法一：因为feq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))＝eq \b\lc\|\rc\|(\a\vs4\al\c1(sin\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))))＋eq \b\lc\|\rc\|(\a\vs4\al\c1(cs\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))))≠f(x)，feq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))＝eq \b\lc\|\rc\|(\a\vs4\al\c1(sin\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))))＋eq \b\lc\|\rc\|(\a\vs4\al\c1(cs\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))))＝|csx|＋|－sinx|＝|csx|＋|sinx|＝f(x)，故排除A，D；最小正周期为eq \f(π,2)，当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))时，f(x)＝sinx＋csx＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))，当x＝0或eq \f(π,2)时，f(x)取得最小值1，所以函数f(x)的最小值是1.故选C.
解法二：由题设，f(x)＝eq \b\lc\{(\a\vs4\al\c1(\r(2)sin\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))，2kπ≤x≤2kπ＋\f(π,2)，,\r(2)sin\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))，2kπ＋\f(π,2)＜x≤2kπ＋π，,－\r(2)sin\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))，2kπ＋π＜x≤2kπ＋\f(3π,2)，,－\r(2)sin\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))，2kπ＋\f(3π,2)＜x≤2（k＋1）π，))
k∈Z，所以f(x)的部分图象如下：
所以最小正周期和最小值分别为eq \f(π,2)，1.故选C.
求三角函数周期的常用方法
1.(2023·长沙雅礼中学一模)函数y＝eq \b\lc\|\rc\|(\a\vs4\al\c1(sin2x＋\f(1,2)))的最小正周期为( )
A．π B．2π
C.eq \f(π,2) D．不能确定
答案 A
解析 作出函数y＝eq \b\lc\|\rc\|(\a\vs4\al\c1(sin2x＋\f(1,2)))的图象如图所示，得到函数的最小正周期为π.故选A.
2．(2023·江西上高一模)若函数f(x)＝2taneq \b\lc\(\rc\)(\a\vs4\al\c1(kx＋\f(π,3)))的最小正周期T满足1答案 2或3
解析 由题意得1角度 三角函数的奇偶性
例4 (1)函数f(x)＝2sin2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋x))－1是( )
A．最小正周期为2π的奇函数
B．最小正周期为π的偶函数
C．最小正周期为2π的偶函数
D．最小正周期为π的奇函数
答案 D
解析 f(x)＝2sin2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋x))－1＝－eq \b\lc\[\rc\](\a\vs4\al\c1(1－2sin2\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)＋x))))＝－cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋2x))＝sin2x，可得f(x)的最小正周期为eq \f(2π,2)＝π.因为f(－x)＝sin(－2x)＝－sin2x＝－f(x)，所以f(x)是奇函数，所以f(x)是最小正周期为π的奇函数．故选D.
(2)(2023·威海三模)已知函数f(x)＝sinx·cs(2x＋φ)(φ∈[0，π])为偶函数，则φ＝( )
A．0 B.eq \f(π,4)
C.eq \f(π,2) D．π
答案 C
解析 ∵f(x)的定义域为R，且为偶函数，∴feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)))＝feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)))⇒cs(π＋φ)＝－cs(－π＋φ)⇒－csφ＝csφ⇒csφ＝0，∵φ∈[0，π]，∴φ＝eq \f(π,2).当φ＝eq \f(π,2)时，f(x)＝－sinxsin2x为偶函数，满足题意．故选C.
解答三角函数奇偶性问题的常用方法
(1)依据奇(偶)函数的定义，即由f(－x)＝－f(x)
(或f(－x)＝f(x))对定义域内任意自变量x都成立，建立关于参数的方程．
(2)由奇(偶)函数的必要条件入手，求出参数的可能取值，再进行验证．
(3)三角函数中奇函数一般可化为y＝Asinωx或y＝Atanωx的形式，而偶函数一般可化为y＝Acsωx＋b的形式．据此结合诱导公式可以确定参数的值．
(4)在y＝Asin(ωx＋φ)(或y＝Acsωx＋b)中代入x＝0，若y＝0，则为奇函数，若y为最大或最小值，则为偶函数．
若函数y＝3cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)＋φ))为奇函数，则|φ|的最小值为________．
答案 eq \f(π,6)
解析 依题意得，－eq \f(π,3)＋φ＝kπ＋eq \f(π,2)(k∈Z)，φ＝kπ＋eq \f(5π,6)(k∈Z)，因此|φ|的最小值是eq \f(π,6).
角度 三角函数的对称性
例5 (1)(多选)(2024·济南模拟)已知函数f(x)＝asinx＋csx(a>0)的最大值为2，则( )
A．a＝eq \r(3)
B．y＝f(x)的图象关于点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，0))对称
C．直线x＝eq \f(π,6)是y＝f(x)图象的一条对称轴
D．y＝f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,3)))上单调递增
答案 AD
解析 易得f(x)＝asinx＋csx＝eq \r(a2＋1)sin(x＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(tanφ＝\f(1,a)))，则f(x)≤eq \r(a2＋1)＝2，解得a＝eq \r(3)，故A正确；由A项分析知f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))，当x＝eq \f(π,6)时，feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))＝2sineq \f(π,3)＝eq \r(3)，故B错误，C错误；当x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,3)))时，x＋eq \f(π,6)∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,2)))，由正弦函数的性质可得，此时y＝f(x)单调递增，故D正确．故选AD.
(2)(2022·新高考Ⅰ卷)记函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(π,4)))＋b(ω>0)的最小正周期为T.若eq \f(2π,3)A．1 B.eq \f(3,2)
C.eq \f(5,2) D．3
答案 A
解析 因为eq \f(2π,3)＜T＜π，所以eq \f(2π,3)＜eq \f(2π,ω)＜π，解得2＜ω＜3.因为y＝f(x)的图象关于点eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，2))中心对称，所以b＝2，且sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)ω＋\f(π,4)))＋b＝2，即sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)ω＋\f(π,4)))＝0，所以eq \f(3π,2)ω＋eq \f(π,4)＝kπ(k∈Z)，又2＜ω＜3，所以eq \f(13π,4)＜eq \f(3π,2)ω＋eq \f(π,4)＜eq \f(19π,4)，所以eq \f(3π,2)ω＋eq \f(π,4)＝4π，解得ω＝eq \f(5,2)，所以f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)x＋\f(π,4)))＋2，所以feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5,2)×\f(π,2)＋\f(π,4)))＋2＝sineq \f(3π,2)＋2＝1.故选A.
求三角函数图象对称中心、对称轴的方法
(1)y＝sinx图象的对称中心是(kπ，0)，k∈Z，对于y＝Asin(ωx＋φ)图象的对称中心，由方程ωx＋φ＝kπ，k∈Z解出x即可．
(2)y＝sinx图象的对称轴是直线x＝kπ＋eq \f(π,2)，k∈Z，由ωx＋φ＝kπ＋eq \f(π,2)，k∈Z解出x，即可得到函数y＝Asin(ωx＋φ)图象的对称轴．
(3)注意y＝tanx图象的对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)，0))(k∈Z)．
(2024·邯郸模拟)写出函数f(x)＝eq \f(csx,1－sinx)图象的一个对称中心：________．
答案 eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，0))(答案不唯一)
解析 f(x)＝eq \f(csx,1－sinx)＝eq \f(cs2\f(x,2)－sin2\f(x,2),\b\lc\(\rc\)(\a\vs4\al\c1(sin\f(x,2)－cs\f(x,2)))\s\up12(2))＝eq \f(cs\f(x,2)＋sin\f(x,2),cs\f(x,2)－sin\f(x,2))＝eq \f(1＋tan\f(x,2),1－tan\f(x,2))＝eq \f(tan\f(x,2)＋tan\f(π,4),1－tan\f(x,2)tan\f(π,4))＝taneq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x,2)＋\f(π,4)))，令eq \f(x,2)＋eq \f(π,4)＝eq \f(kπ,2)(k∈Z)，则x＝－eq \f(π,2)＋kπ(k∈Z)，令k＝0，则x＝－eq \f(π,2)，所以函数f(x)图象的一个对称中心是eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，0)).
课时作业
一、单项选择题
1．函数f(x)＝ln (csx)的定义域为( )
A.eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(kπ－\f(π,2)B.eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(kπC.eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(2kπ－\f(π,2)D.eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(2kπ答案 C
解析 由csx>0，解得2kπ－eq \f(π,2)2．(2023·四川成都模拟)在函数y＝sin|x|，y＝|sinx|，y＝taneq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))，y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))中，最小正周期为π的函数的个数为( )
A．1 B．2
C．3 D．4
答案 C
解析 函数y＝sin|x|的图象如图所示，由图可知，函数y＝sin|x|不是周期函数．
令f(x)＝|sinx|，则f(x＋π)＝|sin(x＋π)|＝|－sinx|＝|sinx|＝f(x)，则函数y＝|sinx|的最小正周期为π，y＝taneq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))的最小正周期为T＝eq \f(π,1)＝π，y＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的最小正周期为T＝eq \f(2π,2)＝π.故选C.
3．(2023·兰州模拟)如图所示，函数y＝csx·|tanx|eq \b\lc\(\rc\)(\a\vs4\al\c1(0≤x<\f(3π,2)且x≠\f(π,2)))的图象是( )
答案 C
解析 y＝csx|tanx|＝eq \b\lc\{(\a\vs4\al\c1(sinx，0≤x<\f(π,2)或π≤x<\f(3π,2)，,－sinx，\f(π,2)4．(2023·长沙模拟)正割(Secant)及余割(Csecant)这两个概念是由伊朗数学家、天文学家阿布尔·威发首先引入，sec，csc这两个符号是荷兰数学家基拉德在《三角学》中首先使用，后经欧拉采用得以通行．在三角中，定义正割secα＝eq \f(1,csα)，余割cscα＝eq \f(1,sinα).则函数f(x)＝eq \f(1,secx)＋eq \f(1,cscx)的值域为( )
A．[－1，1]B．[－eq \r(2)，eq \r(2)]
C．[－2，2]D．[－eq \r(2)，－1)∪(－1，1)∪(1，eq \r(2)]
答案 D
解析 f(x)＝eq \f(1,secx)＋eq \f(1,cscx)＝csx＋sinx＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))，其中sinx≠0，csx≠0，所以－eq \r(2)≤f(x)≤eq \r(2)，且f(x)≠±1，即f(x)的值域为[－eq \r(2)，－1)∪(－1，1)∪(1，eq \r(2)]．故选D.
5．(2023·太原二模)已知函数f(x)＝csx－2cs2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－\f(x,2)))＋1，则下列说法正确的是( )
A．y＝feq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))为奇函数B．y＝feq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))为偶函数
C．y＝feq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))－1为奇函数D．y＝feq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))－1为偶函数
答案 B
解析 因为f(x)＝csx－2cs2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)－\f(x,2)))＋1＝csx－2×eq \f(1＋cs\b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－x)),2)＋1＝csx－sinx＝eq \r(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))，所以f(x)＝eq \r(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))，所以feq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))＝eq \r(2)cseq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))＋\f(π,4)))＝eq \r(2)csx，所以y＝feq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))为偶函数，故A错误，B正确；又y＝feq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))－1＝eq \r(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))－1＝－eq \r(2)sinx－1，所以函数y＝feq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))－1为非奇非偶函数，故C，D错误．故选B.
6．(2023·全国乙卷)已知函数f(x)＝sin(ωx＋φ)在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(2π,3)))单调递增，直线x＝eq \f(π,6)和x＝eq \f(2π,3)为函数y＝f(x)的图象的两条对称轴，则feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(5π,12)))＝( )
A．－eq \f(\r(3),2) B．－eq \f(1,2)
C.eq \f(1,2) D.eq \f(\r(3),2)
答案 D
解析 由题意，eq \f(T,2)＝eq \f(2π,3)－eq \f(π,6)＝eq \f(π,2)，不妨设ω>0，则T＝π，ω＝eq \f(2π,T)＝2，当x＝eq \f(π,6)时，f(x)取得最小值，则2·eq \f(π,6)＋φ＝2kπ－eq \f(π,2)，k∈Z，则φ＝2kπ－eq \f(5π,6)，k∈Z，不妨取k＝0，则f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(5π,6)))，则feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(5π,12)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(5π,3)))＝eq \f(\r(3),2).故选D.
7．(2024·徐州模拟)设α，β均为锐角，则“α>2β”是“sin(α－β)>sinβ”的( )
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
答案 C
解析 因为α，β均为锐角，所以0<α2β时，eq \f(π,2)>α－β>β>0，因为函数y＝sinx在eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)，\f(π,2)))上单调递增，所以sin(α－β)>sinβ，故“α>2β”是“sin(α－β)>sinβ”的充分条件；当sin(α－β)>sinβ时，由0<αβ，即α>2β，故“α>2β”是“sin(α－β)>sinβ”的必要条件．综上所述，“α>2β”是“sin(α－β)>sinβ”的充要条件．
8．(2023·榆林四模)已知函数f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋φ－\f(π,6)))cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋φ＋\f(π,3)))(ω>0)的最小正周期为π，且曲线y＝f(x)关于直线x＝eq \f(π,8)对称，则|φ|的最小值为( )
A.eq \f(π,6) B.eq \f(5π,24)
C.eq \f(7π,24) D.eq \f(π,3)
答案 B
解析 ∵ωx＋φ＋eq \f(π,3)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋φ－\f(π,6)))＋eq \f(π,2)，∴f(x)＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋φ－\f(π,6)))cseq \b\lc\[\rc\](\a\vs4\al\c1(\b\lc\(\rc\)(\a\vs4\al\c1(ωx＋φ－\f(π,6)))＋\f(π,2)))＝－sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋φ－\f(π,6)))cseq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋φ－\f(π,6)))＝－eq \f(1,2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2ωx＋2φ－\f(π,3))).∵f(x)的最小正周期是π，∴eq \f(2π,2ω)＝π，∴ω＝1，则f(x)＝－eq \f(1,2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋2φ－\f(π,3))).∵曲线y＝f(x)关于直线x＝eq \f(π,8)对称，∴2×eq \f(π,8)＋2φ－eq \f(π,3)＝kπ＋eq \f(π,2)，k∈Z，∴φ＝eq \f(kπ,2)＋eq \f(7π,24)，k∈Z，则当k＝0时，|φ|＝eq \f(7π,24)，当k＝－1时，|φ|＝eq \f(5π,24)，则|φ|的最小值为eq \f(5π,24).故选B.
二、多项选择题
9．(2024·山东新高考联合质量测评)已知函数f(x)＝taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))，则下列说法正确的是( )
A．f(x)的最小正周期为eq \f(π,2)
B．f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,3)))上单调递减
C．feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,5)))＝feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))
D．f(x)的定义域为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(π,3)＋kπ，k∈Z))))
答案 AC
解析 因为f(x)＝taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))，对于A，f(x)的最小正周期为T＝eq \f(π,2)，故A正确；对于B，当x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,3)))时，2x－eq \f(π,6)∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,2)))，因为y＝tanz在z∈eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))上单调递增，故f(x)在eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,3)))上单调递增，故B错误；对于C，因为f(x)的最小正周期为T＝eq \f(π,2)，所以feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,5)))＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,5)－\f(π,2)))＝feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(3π,10)))，故C正确；对于D，令2x－eq \f(π,6)≠eq \f(π,2)＋kπ，k∈Z，解得x≠eq \f(π,3)＋eq \f(kπ,2)，k∈Z，所以f(x)的定义域为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(π,3)＋\f(kπ,2)，k∈Z))))，故D错误．故选AC.
10．(2024·保定模拟)若函数f(x)＝2sin3xcs3x＋2cs23x－1，则( )
A．f(x)＝eq \r(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(6x＋\f(π,4)))
B．f(x)的最小正周期为eq \f(π,3)
C．f(x)的图象关于直线x＝eq \f(π,24)对称
D．f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,12)，0))上单调递增
答案 BCD
解析 由题意得f(x)＝sin6x＋cs6x＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(6x＋\f(π,4)))＝eq \r(2)cseq \b\lc\(\rc\)(\a\vs4\al\c1(6x－\f(π,4)))，所以f(x)的最小正周期为eq \f(π,3)，A错误，B正确；因为6×eq \f(π,24)＋eq \f(π,4)＝eq \f(π,2)，所以f(x)的图象关于直线x＝eq \f(π,24)对称，C正确；由x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,12)，0))，得6x＋eq \f(π,4)∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,4)，\f(π,4)))，所以f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,12)，0))上单调递增，D正确．
11．(2023·湖南邵阳一模)随着时代与科技的发展，信号处理以各种方式被广泛应用于医学、声学、密码学、计算机科学、量子力学等各个领域．而信号处理背后的“功臣”就是正弦型函数，f(x)＝eq \i\su(i＝1,4, )eq \f(sin[（2i－1）x],2i－1)的图象就可以近似的模拟某种信号的波形，则下列说法正确的是( )
A．函数f(x)的图象关于直线x＝eq \f(π,2)对称
B．函数f(x)的图象关于点(0，0)对称
C．函数f(x)为周期函数，且最小正周期为π
D．函数f(x)的导函数f′(x)的最大值为4
答案 ABD
解析 因为函数f(x)＝eq \i\su(i＝1,4, )eq \f(sin[（2i－1）x],2i－1)＝sinx＋eq \f(sin3x,3)＋eq \f(sin5x,5)＋eq \f(sin7x,7)，定义域为R，对于A，f(π＋x)＝sin(π＋x)＋eq \f(sin（3π＋3x）,3)＋eq \f(sin（5π＋5x）,5)＋eq \f(sin（7π＋7x）,7)＝－sinx－eq \f(sin3x,3)－eq \f(sin5x,5)－eq \f(sin7x,7)＝sin(－x)＋eq \f(sin（－3x）,3)＋eq \f(sin（－5x）,5)＋eq \f(sin（－7x）,7)＝f(－x)，所以函数f(x)的图象关于直线x＝eq \f(π,2)对称，故A正确；对于B，f(－x)＝sin(－x)＋eq \f(sin（－3x）,3)＋eq \f(sin（－5x）,5)＋eq \f(sin（－7x）,7)＝－sinx－eq \f(sin3x,3)－eq \f(sin5x,5)－eq \f(sin7x,7)＝－f(x)，所以函数f(x)为奇函数，图象关于点(0，0)对称，故B正确；对于C，由题意知f(x＋π)＝－f(x)≠f(x)，故C错误；对于D，由题意可知f′(x)＝csx＋cs3x＋cs5x＋cs7x≤4，故D正确．故选ABD.
三、填空题
12．函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(3π,2)))－3csx的最小值为________．
答案 －4
解析 ∵f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(3π,2)))－3csx＝－cs2x－3csx＝－2cs2x－3csx＋1＝－2eq \b\lc\(\rc\)(\a\vs4\al\c1(csx＋\f(3,4)))eq \s\up12(2)＋eq \f(17,8)，－1≤csx≤1，∴当csx＝1时，f(x)有最小值－4.
13．已知f(x)＝sineq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)（x＋1）))－eq \r(3)cseq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)（x＋1）))，则f(x)的最小正周期为________，f(1)＋f(2)＋…＋f(2023)＝________．
答案 6 eq \r(3)
解析 依题意可得f(x)＝2sineq \f(π,3)x，其最小正周期T＝6，且f(1)＋f(2)＋…＋f(6)＝0，故f(1)＋f(2)＋…＋f(2023)＝f(1)＝eq \r(3).
14．(2023·泰州模拟)当θ＝θ0时，f(θ)＝sin2θ－cs2θ取得最大值，则sineq \b\lc\(\rc\)(\a\vs4\al\c1(2θ0＋\f(π,4)))＝________．
答案 eq \f(\r(10),10)
解析 f(θ)＝sin2θ－eq \f(1,2)(1＋cs2θ)＝sin2θ－eq \f(1,2)cs2θ－eq \f(1,2)＝eq \f(\r(5),2)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(5),5)sin2θ－\f(\r(5),5)cs2θ))－eq \f(1,2)＝eq \f(\r(5),2)sin(2θ－φ)－eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(其中csφ＝\f(2\r(5),5)，sinφ＝\f(\r(5),5)))，当f(θ)取得最大值时，2θ0－φ＝eq \f(π,2)＋2kπ，k∈Z，所以2θ0＝φ＋eq \f(π,2)＋2kπ，k∈Z，所以sin2θ0＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(φ＋\f(π,2)＋2kπ))＝csφ＝eq \f(2\r(5),5)，cs2θ0＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(φ＋\f(π,2)＋2kπ))＝－sinφ＝－eq \f(\r(5),5)，所以sineq \b\lc\(\rc\)(\a\vs4\al\c1(2θ0＋\f(π,4)))＝eq \f(\r(2),2)sin2θ0＋eq \f(\r(2),2)cs2θ0＝eq \f(\r(2),2)×eq \f(2\r(5),5)＋eq \f(\r(2),2)×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(5),5)))＝eq \f(\r(10),10).
四、解答题
15．已知函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))＋eq \f(\r(3),2).
(1)求函数f(x)的最小正周期及其图象的对称中心；
(2)若f(x0)≤eq \r(3)，求x0的取值范围．
解 (1)函数f(x)的最小正周期T＝π.
由2x－eq \f(π,3)＝kπ，k∈Z得x＝eq \f(π,6)＋eq \f(kπ,2)，k∈Z，
故函数f(x)图象的对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)＋\f(kπ,2)，\f(\r(3),2)))，k∈Z.
(2)因为f(x0)≤eq \r(3)，
所以sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x0－\f(π,3)))＋eq \f(\r(3),2)≤eq \r(3)，
即sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x0－\f(π,3)))≤eq \f(\r(3),2)，
所以－eq \f(4π,3)＋2kπ≤2x0－eq \f(π,3)≤eq \f(π,3)＋2kπ，k∈Z，
即－eq \f(π,2)＋kπ≤x0≤eq \f(π,3)＋kπ，k∈Z.
即x0的取值范围为eq \b\lc\{\rc\}(\a\vs4\al\c1(x0\b\lc\|(\a\vs4\al\c1(－\f(π,2)＋kπ≤x0≤\f(π,3)＋kπ，k∈Z)))).
16．已知函数f(x)＝2sinxcsx＋cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))＋cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))，x∈R.
(1)求feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)))的值；
(2)求函数f(x)在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，π))上的最大值和最小值，及相应的x的值；
(3)求函数f(x)在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，π))上的单调区间．
解 (1)∵f(x)＝2sinxcsx＋cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6)))＋cseq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))＝sin2x＋cs2xcseq \f(π,6)＋sin2xsineq \f(π,6)＋cs2xcseq \f(π,6)－sin2xsineq \f(π,6)＝sin2x＋eq \r(3)cs2x＝2eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)sin2x＋\f(\r(3),2)cs2x))＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))，
∴feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,12)))＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(π,12)＋\f(π,3)))＝2sineq \f(π,2)＝2.
(2)∵eq \f(π,2)≤x≤π，∴eq \f(4π,3)≤2x＋eq \f(π,3)≤eq \f(7π,3)，
∴－2≤f(x)≤eq \r(3)，
当2x＋eq \f(π,3)＝eq \f(3π,2)时，x＝eq \f(7π,12)，此时f(x)min＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(7π,12)))＝－2，
当2x＋eq \f(π,3)＝eq \f(7π,3)时，x＝π，此时f(x)max＝f(π)＝eq \r(3).
(3)∵eq \f(π,2)≤x≤π，∴eq \f(4π,3)≤2x＋eq \f(π,3)≤eq \f(7π,3)，
由正弦函数图象知，
当eq \f(4π,3)≤2x＋eq \f(π,3)≤eq \f(3π,2)，即eq \f(π,2)≤x≤eq \f(7π,12)时，f(x)单调递减；
当eq \f(3π,2)≤2x＋eq \f(π,3)≤eq \f(7π,3)，即eq \f(7π,12)≤x≤π时，f(x)单调递增．
故函数f(x)在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，π))上的单调递减区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)，\f(7π,12)))，单调递增区间为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,12)，π)).
17．(2023·四省高考适应性测试)已知函数f(x)＝sin(ωx＋φ)在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,2)))上单调，其中ω为正整数，|φ|(1)求y＝f(x)图象的一条对称轴；
(2)若feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))＝eq \f(\r(3),2)，求φ.
解 (1)因为函数f(x)＝sin(ωx＋φ)在区间eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)，\f(π,2)))上单调，所以函数f(x)的最小正周期T≥2×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)－\f(π,6)))＝eq \f(2π,3)，
又因为feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)))＝feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2π,3)))，
所以直线x＝eq \f(1,2)×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋\f(2π,3)))＝eq \f(7π,12)为y＝f(x)图象的一条对称轴．
(2)由(1)知T≥eq \f(2π,3)，故ω＝eq \f(2π,T)≤3，由ω∈N*，得ω＝1，2或3.
因为直线x＝eq \f(7π,12)为f(x)＝sin(ωx＋φ)图象的一条对称轴，所以eq \f(7π,12)ω＋φ＝eq \f(π,2)＋k1π，k1∈Z.
因为feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))＝eq \f(\r(3),2)，所以eq \f(π,6)ω＋φ＝eq \f(π,3)＋2k2π或eq \f(π,6)ω＋φ＝eq \f(2π,3)＋2k3π，k2，k3∈Z，
若eq \f(π,6)ω＋φ＝eq \f(π,3)＋2k2π，k2∈Z，则eq \f(5π,12)ω＝eq \f(π,6)＋(k1－2k2)π，k1，k2∈Z，即ω＝eq \f(2,5)＋eq \f(12,5)(k1－2k2)，k1，k2∈Z，
不存在整数k1，k2，使得ω＝1，2或3；
若eq \f(π,6)ω＋φ＝eq \f(2π,3)＋2k3π，k3∈Z，则eq \f(5π,12)ω＝－eq \f(π,6)＋(k1－2k3)π，k1，k3∈Z，即ω＝－eq \f(2,5)＋eq \f(12,5)(k1－2k3)，k1，k3∈Z，
不存在整数k1，k3，使得ω＝1或3.当k1＝2k3＋1时，ω＝2.
此时φ＝eq \f(π,3)＋2k3π，k3∈Z，
由|φ|18.(2023·海口调研)如图，已知OPQ是半径为1，圆心角为eq \f(π,3)的扇形，点A在eq \(PQ,\s\up12(︵))上(异于点P，Q)，过点A作AB⊥OP，AC⊥OQ，垂足分别为B，C，记∠AOB＝θ，四边形ACOB的周长为l.
(1)求l关于θ的函数关系式；
(2)当θ为何值时，l有最大值？并求出l的最大值．
解 (1)AB＝OAsinθ＝sinθ，OB＝OAcsθ＝csθ，
AC＝OAsineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－θ))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－θ))，
OC＝OAcseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－θ))＝cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－θ))，
所以l＝sinθ＋csθ＋sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－θ))＋cseq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－θ))＝sinθ＋csθ＋eq \f(\r(3),2)csθ－eq \f(1,2)sinθ＋eq \f(1,2)csθ＋eq \f(\r(3),2)sinθ＝eq \f(1＋\r(3),2)sinθ＋eq \f(3＋\r(3),2)csθ＝eq \f(\r(3)＋1,2)(sinθ＋eq \r(3)csθ)＝(eq \r(3)＋1)sineq \b\lc\(\rc\)(\a\vs4\al\c1(θ＋\f(π,3)))eq \b\lc\(\rc\)(\a\vs4\al\c1(0<θ<\f(π,3))).
(2)由0<θ当θ＋eq \f(π,3)＝eq \f(π,2)，即θ＝eq \f(π,6)时，sineq \b\lc\(\rc\)(\a\vs4\al\c1(θ＋\f(π,3)))＝1，
lmax＝eq \r(3)＋1，
所以当θ＝eq \f(π,6)时，lmax＝eq \r(3)＋1.函数
y＝sinx
y＝csx
y＝tanx
图象
定义域
eq \x(\s\up1(01))R
eq \x(\s\up1(02))R
eq \x(\s\up1(03))eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x∈R且x≠\f(π,2)＋kπ，k∈Z))))
值域
eq \x(\s\up1(04))[－1，1]
eq \x(\s\up1(05))[－1，1]
eq \x(\s\up1(06))R
单调性
在eq \x(\s\up1(07))eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)＋2kπ，\f(π,2)＋2kπ))(k∈Z)上递增；
在eq \x(\s\up1(08))eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,2)＋2kπ，\f(3π,2)＋2kπ))(k∈Z)上递减
在eq \x(\s\up1(09))[(2k－1)π，2kπ](k∈Z)上递增；在eq \x(\s\up1(10))[2kπ，(2k＋1)π](k∈Z)上递减
在eq \x(\s\up1(11))eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2)＋kπ，\f(π,2)＋kπ))(k∈Z)上递增
最值
x＝eq \x(\s\up1(12))eq \f(π,2)＋2kπ(k∈Z)时，ymax＝1；
x＝eq \x(\s\up1(13))－eq \f(π,2)＋2kπ(k∈Z)时，ymin＝－1
x＝eq \x(\s\up1(14))2kπ(k∈Z)时，ymax＝1；
x＝eq \x(\s\up1(15))π＋2kπ(k∈Z)时，ymin＝－1
无最值
奇偶性
eq \x(\s\up1(16))奇函数
eq \x(\s\up1(17))偶函数
eq \x(\s\up1(18))奇函数
对称性
对称中心
eq \x(\s\up1(19))(kπ，0)，k∈Z
eq \x(\s\up1(20))eq \b\lc\(\rc\)(\a\vs4\al\c1(kπ＋\f(π,2)，0))，k∈Z
eq \x(\s\up1(21))eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)，0))，k∈Z
对称轴
eq \x(\s\up1(22))直线x＝kπ＋eq \f(π,2)，k∈Z
eq \x(\s\up1(23))直线x＝kπ，k∈Z
无对称轴
最小正周期
eq \x(\s\up1(24))2π
eq \x(\s\up1(25))2π
eq \x(\s\up1(26))π
考向一 三角函数的定义域和值域
考向二 三角函数的单调性
考向三 三角函数的周期性、奇偶性、对称性