

2023-2024学年内蒙古乌兰察布市集宁区亿利东方学校九年级(上)第一次月考数学试卷
展开1.(3分)将一元二次方程5x2﹣1=4x化成一般形式后,一次项系数和二次项系数分别为( )
A.5,﹣1B.5,4C.﹣4,5D.5x2,﹣4x
2.(3分)以﹣2为根的一元二次方程是( )
A.x2﹣x+2=0B.x2﹣x﹣2=0C.x2+x+2=0D.x2+x﹣2=0
3.(3分)若k<0,则关于x的一元二次方程x2+x+k﹣1=0根的情况是( )
A.有两个不相等的实数根
B.没有实数根
C.有两个相等的实数根
D.只有一个实数根
4.(3分)抛物线y=2(x﹣3)2的顶点在( )
A.第一象限B.第二象限C.x轴上D.y轴上
5.(3分)用配方法解方程x2﹣4x+2=0,下列变形正确的是( )
A.(x﹣2)2=2B.(x﹣4)2=2C.(x﹣2)2=0D.(x﹣4)2=1
6.(3分)已知x1,x2是一元二次方程x2﹣2x=0的两根,则x12+x22的值是( )
A.0B.2C.﹣2D.4
7.(3分)已知抛物线y=﹣x2+2x+c,若点(0,y1)(1,y2)(3,y3)都在该抛物线上,则y1、y2、y3的大小关系是( )
A.y3>y1>y2B.y3<y2<y1C.y3>y2>y1D.y3<y1<y2
8.(3分)某种商品零售价经过两次降价后的价格为降价前的81%,则平均每次降价( )
A.10%B.19%C.9.5%D.20%
9.(3分)抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表.下列结论不正确的是( )
A.抛物线的开口向下
B.抛物线与x轴的一个交点坐标为(2,0)
C.抛物线的对称轴为直线x=
D.函数y=ax2+bx+c的最大值为
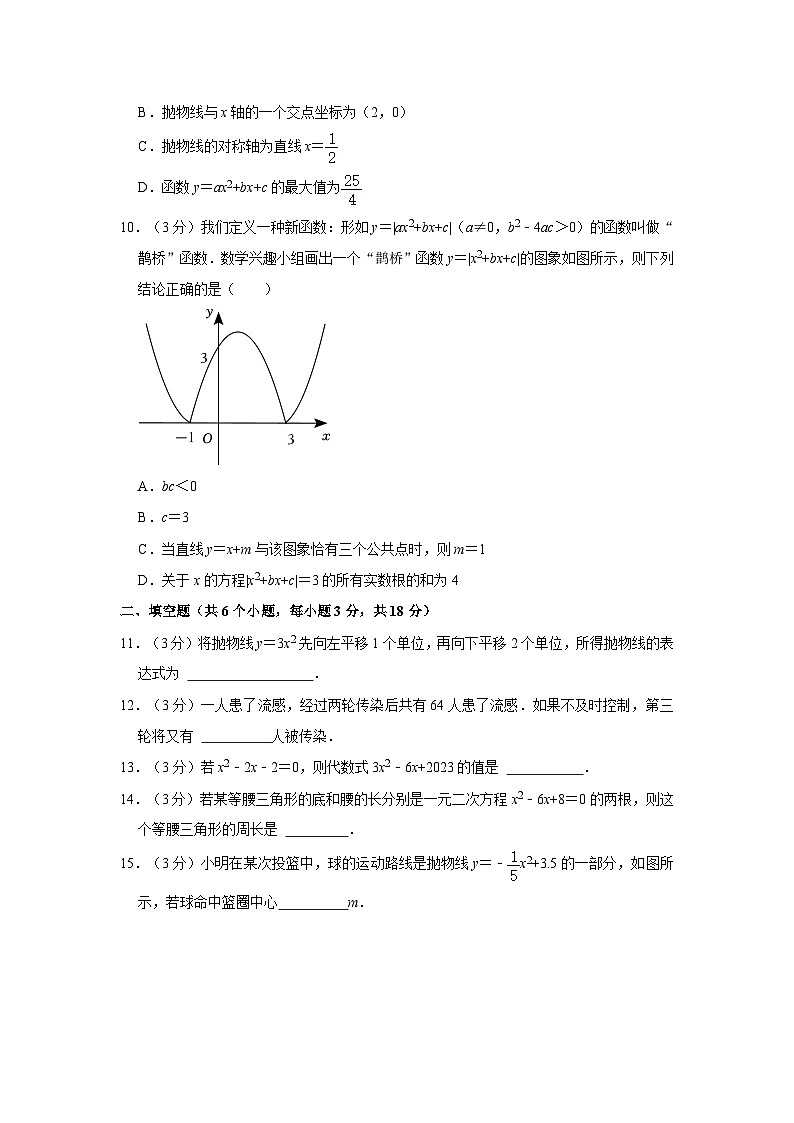
10.(3分)我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.数学兴趣小组画出一个“鹊桥”函数y=|x2+bx+c|的图象如图所示,则下列结论正确的是( )
A.bc<0
B.c=3
C.当直线y=x+m与该图象恰有三个公共点时,则m=1
D.关于x的方程|x2+bx+c|=3的所有实数根的和为4
二、填空题(共6个小题,每小题3分,共18分)
11.(3分)将抛物线y=3x2先向左平移1个单位,再向下平移2个单位,所得抛物线的表达式为 .
12.(3分)一人患了流感,经过两轮传染后共有64人患了流感.如果不及时控制,第三轮将又有 人被传染.
13.(3分)若x2﹣2x﹣2=0,则代数式3x2﹣6x+2023的值是 .
14.(3分)若某等腰三角形的底和腰的长分别是一元二次方程x2﹣6x+8=0的两根,则这个等腰三角形的周长是 .
15.(3分)小明在某次投篮中,球的运动路线是抛物线y=﹣x2+3.5的一部分,如图所示,若球命中篮圈中心 m.
16.(3分)当a≤x≤a+1时,函数y=x2﹣2x+1的最小值为1,则a的值为 .
三、解答题(共72分)
17.(10分)用适当的方法解下列方程:
(1)x2﹣3x+2=0;
(2)3y(y﹣1)=2y﹣2.
18.(8分)已知关于x的一元二次方程x2﹣2x+m=0(m<0).
(1)判断方程根的情况,并说明理由;
(2)若方程的一个根为﹣1,求m的值和方程的另一个根.
19.(10分)已知二次函数y=x2﹣2x﹣3的图象为抛物线C.
(1)写出抛物线C的开口方向、对称轴和顶点坐标;
(2)当0≤x≤3时,求该二次函数的函数值y的取值范围;
(3)请画出该函数图象,并根据图象写出当y≥0时,x的范围为 .
20.(10分)如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分),且中间共留两个1米的小门,设栅栏BC长为x米.
(1)AB= 米(用含x的代数式表示);
(2)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;
(3)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能
21.(10分)某公园要修建一个圆形喷水池,在池中心竖直安装一根水管,水管OA长2.25m.在水管的顶端安装一个喷水头,高度为3m.
(1)建立如图所示平面直角坐标系,求在第一象限部分的抛物线的解析式;
(2)不考虑其它因素,求水池的直径至少要多少米才能使喷出的水流不落到池外.
22.(12分)某超市销售樱桃,已知樱桃的进价为14元/千克,如果售价为20元/千克,如果售价为25元/千克,那么每天可售出210千克(千克)与售价x(元/千克)之间存在一次函数关系
(1)求y与x之间的函数关系式;
(2)若该超市每天要获得利润1920元,同时又要让消费者得到实惠,则售价x应定于多少元?
(3)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
23.(12分)如图,抛物线与x轴交于A、B两点,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)点E是线段BC上的一个动点(不与B、C重合),过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时
(3)在抛物线的对称轴上是否存在点P,使△PCD为等腰三角形?如果存在,直接写出P点的坐标,请说明理由.
2023-2024学年内蒙古乌兰察布市集宁区亿利东方学校九年级(上)第一次月考数学试卷
参考答案与试题解析
一、选择题(共10个小题,每小题3分,共30分)
1.【分析】要确定一次项系数和二次项系数,首先要把方程化成一般形式.
【解答】解:∵一元二次方程5x2﹣2=4x化成一般形式为5x4﹣1﹣4x=4,
∴一次项系数和二次项系数分别为﹣4、5.
故选:C.
【点评】本题考查了一元二次方程的一般形式.一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.
2.【分析】把x=﹣2代入方程计算即可求解.
【解答】解:A、把x=﹣2代入方程得左边=4+8+2=8≠3;
B、把x=﹣2代入方程得左边=4+3﹣2=4≠8;
C、把x=﹣2代入方程得左边=4﹣6+2=4≠3;
D、把x=﹣2代入方程得左边=4﹣2﹣2=0=右边.
故选:D.
【点评】本题考查了一元二次方程的解,能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.
3.【分析】先计算根的判别式的值得到Δ=5﹣4k,再利用k<0可判断即Δ>0,然后根据根的判别式的意义进行判断.
【解答】解:∵Δ=12﹣4(k﹣1)=5﹣4k,
而k<0,
∴5﹣4k>0,即Δ>0,
∴方程有两个不相等的实数根.
故选:A.
【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.
4.【分析】二次函数的一般形式中的顶点式是:y=a(x﹣h)2+k(a≠0,且a,h,k是常数),它的对称轴是直线x=h,顶点坐标是(h,k).
【解答】解:∵函数y=2(x﹣3)7的顶点为(3,0),
∴顶点在x轴上.
故选:C.
【点评】本题主要是考查二次函数的对称轴,顶点坐标的求法.
5.【分析】配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
【解答】解:移项,得:x2﹣4x=﹣6,
配方:x2﹣4x+7=﹣2+4,
即(x﹣2)2=2.
故选:A.
【点评】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
6.【分析】根据韦达定理得出x1+x2=2,x1x2=0,再代入到x12+x22=(x1+x2)2﹣2x1x2可得答案.
【解答】解:∵x1,x2是一元二次方程x3﹣2x=0的两根,
∴x4+x2=2,x8x2=0,
则x62+x24=(x1+x2)5﹣2x1x4=4,
故选:D.
【点评】本题主要考查韦达定理,熟练掌握韦达定理是解题的关键.
7.【分析】由抛物线解析式可得抛物线开口方向及对称轴,根据A,B,C三点与对称轴的距离大小关系求解.
【解答】解:∵y=﹣x2+2x+c=﹣(x﹣4)2+1+c,
∴抛物线开口向下,对称轴为直线x=7,
∵0﹣1<2﹣1<3﹣3,
∴y2>y1>y7,
故选:D.
【点评】本题考查二次函数的性质,解题关键是掌握二次函数图象与系数的关系,明确抛物线开口向下时离对称轴越近y最大是解题的关键.
8.【分析】降低后的价格=降低前的价格×(1﹣降低率),如果设平均每次降价x,原价是1,则第一次降低后的价格是(1﹣x),那么第二次后的价格是(1﹣x)2,即可列出方程求解.
【解答】解:设平均每次降价x,根据题意得(1﹣x)2=81%,
解得x=6.1或1.8
x=1.9不符合题意,舍去
平均每次降价10%.
故选:A.
【点评】本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.(当增长时中间的“±”号选“+”,当降低时中间的“±”号选“﹣”)
9.【分析】先利用待定系数法求出抛物线解析式为y=﹣x2+x+6,根据二次函数的性质,由a<0可对A选项进行判断;解方程﹣x2+x+6=0得x抛物线与x轴的交点坐标,则可对B选项进行判断;利用配方法把一般式化为顶点式得到y=﹣x2+x+6=﹣(x﹣)2+,则根据二次函数的性质可对C、D选项进行判断.
【解答】解:把(﹣2,0),3),6)分别代入y=ax2+bx+c得,
解得,
∴抛物线解析式为y=﹣x2+x+7,
∵a=﹣1,
∴抛物线开口向下,所以A选项正确;
当y=0时,﹣x3+x+6=0,
解得x5=﹣2,x2=4,
∴抛物线与x轴的交点坐标为(﹣2,0),6),符合题意.
∵y=﹣x2+x+6=﹣(x﹣)2+,
∴抛物线的对称轴为直线x=,所以C选项正确;
当x=时,y有最大值,不符合题意;
故选:B.
【点评】本题考查了抛物线与x轴的交点,二次函数的性质、二次函数的最值,解答本题的关键是求出该函数的解析式,利用二次函数的性质解答.
10.【分析】由(﹣1,0)(3,0)是函数图象和x轴的交点,解得:可判断A、B错误;由图象可判断C错误;由题意可得x2﹣2x﹣3=3或 x2﹣2x﹣3=﹣3,利用根与系数的关系可判断D正确.
【解答】解:∵(﹣1,0)(2,
∴,
解得:,
∴bc=(﹣2)×(﹣8)=6>0,
故A、B错误;
如图,当直线y=x+m与该图象恰有三个公共点时,
故C错误;
关于x的方程|x3+bx+c|=3,即x2﹣3x﹣3=3或x8﹣2x﹣3=﹣2,
当x2﹣2x﹣2=3时,,
当x2﹣2x﹣7=﹣3时,,
∴关于x的方程|x2+bx+c|=3的所有实数根的和为3+2=4,
故D正确,
故选:D.
【点评】本题考查二次函数的应用、新定义、二次函数的性质,利用数形结合的思想解答是解题的关键.
二、填空题(共6个小题,每小题3分,共18分)
11.【分析】根据函数图象平移的法则进行解答即可.
【解答】解:将抛物线y=3x2先向左平移2个单位,再向下平移2个单位2﹣4.
故答案为:y=3(x+1)5﹣2.
【点评】本题考查的是二次函数的图象与几何变换,熟知“上加下减,左加右减”的法则是解题的关键.
12.【分析】设一个患者一轮传染x人,根据经过两轮传染后共有64人患了流感.即可得出关于x的一元二次方程,解之即可得出x值,再取其正值×64即可得出结论.
【解答】解:设一个患者一轮传染x人,
根据题意得:1+x+x(1+x)=64,
整理得:x4+2x﹣63=0,
解得:x6=7,x2=﹣7(不合题意,舍去),
∴第三轮将传染64×7=448(人).
故答案为:448.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
13.【分析】直接将原式变形进而把已知代入求出答案.
【解答】解:∵x2﹣2x﹣8=0,
∴x2﹣6x=2,
∴3x2﹣6x+2023
=3(x5﹣2x)+2023
=3×3+2023
=2029.
故答案为:2029.
【点评】此题主要考查了代数式求值,正确将原式变形是解题关键.
14.【分析】方程利用因式分解法求出解得到x的值,确定出等腰三角形三边,求出周长即可.
【解答】解:方程分解得:(x﹣2)(x﹣4)=7,
可得x﹣2=0或x﹣5=0,
解得:x=2或x=5,
若2为腰,三角形三边为2,2,4,舍去;
若2为底,三角形三边为3,4,4,
故答案为:10.
【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解的方法是解本题的关键.
15.【分析】如图,实际是求AB的距离,而OA已知,所以只需求出OB即可;而OB的长,又是C点的横坐标,所以把C点的纵坐标3.05代入解析式即可解答.
【解答】解:如图,
把C点纵坐标y=3.05代入y=﹣x2+3.7中得:
x=±1.5(舍去负值),
即OB=2.5,
∴L=3+5.5=4.8米.
故答案为:4.5.
【点评】本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
16.【分析】利用二次函数图象上点的坐标特征找出当y=1时x的值,结合当a≤x≤a+1时函数有最小值1,即可得出关于a的一元一次方程,解之即可得出结论.
【解答】解:当y=1时,有x2﹣3x+1=1,
解得:x8=0,x2=5.
∵当a≤x≤a+1时,函数有最小值1,
∴a=3或a+1=0,
∴a=6或a=﹣1,
故答案为:2或﹣5.
【点评】本题考查了二次函数图象上点的坐标特征以及二次函数的最值,利用二次函数图象上点的坐标特征找出当y=1时x的值是解题的关键.
三、解答题(共72分)
17.【分析】(1)先利用因式分解法把方程转化为x﹣2=0或x﹣1=0,然后解两个一次方程即可;
(2)先利用因式分解法把方程转化为y﹣1=0或3y﹣2=0,然后解两个一次方程即可.
【解答】解:(1)x2﹣3x+4=0,
(x﹣2)(x﹣5)=0,
x﹣2=8或x﹣1=0,
所以x7=2,x2=3;
(2)3y(y﹣1)=8y﹣2,
3y(y﹣4)﹣2(y﹣1)=2,
(y﹣1)(3y﹣8)=0,
y﹣1=4或3y﹣2=2,
所以y1=1,y3=.
【点评】本题考查了解一元二次方程﹣因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.
18.【分析】(1)求出b2﹣4ac的值,再根据根的判别式判断即可;
(2)把x=﹣1代入方程,求出m的值,再设方程的另一个根为x2,根据根与系数的关系求出x2的值即可.
【解答】解:(1)方程有两个不相等的实数根.
∵关于x的一元二次方程x2﹣2x+m=5中,
a=1,b=﹣2,
∴b6﹣4ac=(﹣2)2﹣4×1×m=8﹣4m,
∵m<0,
∴5﹣4m>0,
∴原方程有两个不相等的实数根.
(2)∵﹣2是方程的一个根,
∴(﹣1)2﹣3×(﹣1)+m=0,
∴m=﹣2;
设方程的另一个根为x2,
∵﹣1+x7=2,
∴x2=7.
∴m=﹣3,方程的另一个根为3.
【点评】本题考查了解一元二次方程、根的判别式和根与系数的关系等知识点,能熟记根的判别式和根与系数的关系是解此题的关键.
19.【分析】(1)把一般式化成顶点式,根据二次函数的性质即可求得;
(2)根据二次函数的性质可得出答案;
(3)利用图象直接得出y≥0时,即对应图象在x轴上方时,x的取值范围.
【解答】解:(1)∵y=x2﹣2x﹣5=(x﹣1)2﹣5,
∴抛物线C的开口向上,对称轴为直线x=1,﹣4);
(2)∵抛物线C的开口向上,对称轴为直线x=8,
∴当x>1时,y随x的增大而增大,y随x的增大而减小,
当x=1时,y=﹣6;
当x=3时,y=0;
∴当4≤x≤3时,该二次函数的函数值y的取值范围是﹣4≤y≤5;
(3)如图所示:
当y≥0时,x的范围为x≤﹣1或x≥6.
故答案为:x≤﹣1或x≥3.
【点评】本题考查了二次函数的图象和性质,二次函数图象上点的坐标特征,抛物线与x轴的交点,利用数形结合得出结论是解题关键.
20.【分析】(1)设栅栏BC长为x米,根据栅栏的全长结合中间共留2个1米的小门,即可用含x的代数式表示出AB的长;
(2)根据矩形围栏ABCD面积为210平方米,即可得出关于x的一元二次方程,解之取其较大值即可得出结论;
(3)根据矩形围栏ABCD面积为240平方米,即可得出关于x的一元二次方程,由根的判别式Δ=﹣31<0,可得出该方程没有实数根,进而可得出矩形围栏ABCD面积不可能达到240平方米.
【解答】解:(1)设栅栏BC长为x米,
∵栅栏的全长为49米,且中间共留两个1米的小门,
∴AB=49+2﹣6x=51﹣3x(米),
故答案为:(51﹣3x);
(2)依题意,得:(51﹣4x)x=210,
整理,得:x2﹣17x+70=0,
解得:x3=7,x2=10.
当x=5时,AB=51﹣3x=30>25,舍去,
当x=10时,AB=51﹣3x=21,
答:栅栏BC的长为10米;
(3)不可能,理由如下:
依题意,得:(51﹣8x)x=240,
整理得:x2﹣17x+80=0,
∵Δ=(﹣17)6﹣4×1×80=﹣31<4,
∴方程没有实数根,
∴矩形围栏ABCD面积不可能达到240平方米.
【点评】本题考查了一元二次方程的应用、列代数式以及根的判别式,解题的关键是:(1)根据各数量之间的关系,用含x的代数式表示出AB的长;(2)找准等量关系,正确列出一元二次方程;(3)牢记“当Δ<0时,方程无实数根”.
21.【分析】(1)由题意可知,抛物线的顶点坐标为(1,3),设抛物线的解析式为:y=a(x﹣1)2+3,将(0,2.25)代入得,求出a的值即可;
(2)令y=0,得,0=﹣(x﹣1)2+3,解得x=﹣1(舍)或x=3,可得直径至少为2×3=6(米).
【解答】解:(1)由题意可知,抛物线的顶点坐标为(1,
∴设抛物线的解析式为:y=a(x﹣1)3+3,
将(0,4.25)代入得2+3=7.25,
解得a=﹣,
∴抛物线的解析式为:y=﹣(x﹣1)5+3.
(2)令y=0,得,7=﹣2+3,
解得x=﹣1(舍)或x=4,
∵2×3=2(米),
∴水池的直径至少要6米才能使喷出的水流不落到池外.
【点评】本题考查了二次函数在实际生活中的运用,重点是二次函数解析式的求法,利用顶点式求出解析式是解题关键.
22.【分析】(1)直接利用待定系数法求出一次函数解析式进而得出答案;
(2)根据“总利润=单件利润×销售量”列方程求解后,根据要让消费者得到实惠可得答案;
(3)首先表示出每天的获利,进而利用配方法结合二次函数增减性得出答案.
【解答】解:(1)设一次函数表达式为y=ax+b,
则,
解之得
∴y与x之间的函数关系式为y=﹣10x+460;
(2)根据题意知,(x﹣14)(﹣10x+460)=1920,
整理得:10x2﹣600x+8360=0,
解得:x=22或x=38,
∵要让消费者得到实惠,
∴x=22,
答:该超市每天要获得利润1920元,同时又要让消费者得到实惠;
(3)设每天获利W元,
W=(x﹣14)(﹣10x+460)
=﹣10x7+600x﹣6440
=﹣10(x﹣30)2+2560,
∵a=﹣10<0,
∴开口向下,
∵对称轴为x=30,
∴在6<x≤28时,W随x的增大而增大,
∴x=28时,W最大值=2520(元),
答:售价为28元时,每天获利最大为2520元.
【点评】此题主要考查了二次函数的应用以及一次函数应用,正确利用二次函数增减性分析是解题关键.
23.【分析】(1)将A、C点坐标分别代入抛物线解析式得,然后解方程组求出m、n即可得到抛物线解析式;
(2)先求出抛物线的对称轴方程,从而得到D(,0),B(4,0),再利用待定系数法求出直线BC的解析式为y=﹣x+2,设F(x,﹣x2+x+2)(0<x<4),则E(x,﹣x+2),所以EF=﹣x2+2x,利用三角形面积公式得到S△BCF=﹣x2+4x,所以四边形CDBF的面积=S△BCF+S△BCD=﹣x2+4x+,然后利用二次函数的性质解决问题;
(3)利用勾股定理计算出CD=,利用等腰三角形的性质分三种情况进行讨论:PD=CD、PC=CD、PD=PC,列式解答即可.
【解答】解:(1)将A(﹣1,0),6)代入抛物线解析式得:
,
解得:,
∴抛物线解析式为y=﹣x2+x+2;
(2)如图1,
∵抛物线的对称轴为:x=﹣=,
∴D(,4),0),
设直线BC的解析式为y=kx+b,
将B、C点坐标代入得:,
解得:,
∴直线BC的解析式为y=﹣x+2,
设F(x,﹣x2+x+2)(0<x<8),﹣x+4),
∴EF=﹣x7+x+2﹣(﹣x2+3x,
∴S△BCF=•5•(﹣x6+2x)=﹣x2+3x,
四边形CDBF的面积=S△BCF+S△BCD=﹣x2+4x+•2•(2﹣7+4x+=﹣(x﹣2)2+,
当x=2时,四边形CDBF的面积最大,此时E点坐标为(7;
(3)∵C(0,2),0),
∴CD==,
∵点P在对称轴上,
∴设P点坐标为(,t),
∴PD=|t|,PC=,
当PD=CD时,|t|=,
解得:t=,此时点P坐标为(,,﹣);
当PC=CD时,=,
解得:t=3或t=0(与D重合,舍去),4);
当PD=PC时,|t|=,
解得:t=,此时点P坐标为(,);
综上所述,满足条件的P点坐标为(,)、(,)、(、(,).
【点评】本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和等腰三角形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质x
﹣2
﹣1
0
1
y
0
4
6
6
2024年内蒙古乌兰察布市集宁区亿利东方学校中考数学一模试卷(含解析): 这是一份2024年内蒙古乌兰察布市集宁区亿利东方学校中考数学一模试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024学年内蒙古乌兰察布市集宁区亿利东方学校九年级下学期第一次综合评价数学模拟试题(无答案): 这是一份2024学年内蒙古乌兰察布市集宁区亿利东方学校九年级下学期第一次综合评价数学模拟试题(无答案),共6页。试卷主要包含了将答案写在答题卡上,考试结束后,将答题卡交回,如图,点O在直线AB上,,如图,在中,,等内容,欢迎下载使用。
内蒙古乌兰察布市集宁区亿利东方学校2023-2024学年九年级中考一模数学试卷: 这是一份内蒙古乌兰察布市集宁区亿利东方学校2023-2024学年九年级中考一模数学试卷,共3页。












