2021-2022学年北京市海淀区清华附中八年级（上）期中数学试卷【含解析】

这是一份2021-2022学年北京市海淀区清华附中八年级（上）期中数学试卷【含解析】，共28页。试卷主要包含了选择题，填空题，解答题，附加题等内容，欢迎下载使用。

1．（3分）现实生活中，对称现象无处不在，中国的汉字中有些也具有对称性，下列字是轴对称图形的是（ ）
A．诚B．信C．友D．善
2．（3分）已知一个正方形边长为a+1，则该正方形的面积为（ ）
A．a2+2a+1B．a2﹣2a+1C．a2+1D．2a+1
3．（3分）已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（ ）
A．10B．15C．17D．19
4．（3分）下列各式运算结果为a9的是（ ）
A．a6+a3B．a3•a3C．（a3）3D．a18÷a2
5．（3分）如图，在△ABC中，AB＝AC，AD、CE分别是△ABC的中线和角平分线．若∠CAD＝20°，则∠ACE的度数是（ ）
A．20°B．35°C．40°D．70°
6．（3分）下列多项式中能用平方差公式分解因式的是（ ）
A．﹣a2﹣b2B．x2+（﹣y）2
C．（﹣x）2+（﹣y）2D．﹣m2+1
7．（3分）如图，网格中的每个小正方形边长均为1，△ABC的顶点均落在格点上，若点A的坐标为（﹣2，﹣1），则到△ABC三个顶点距离相等的点的坐标为（ ）
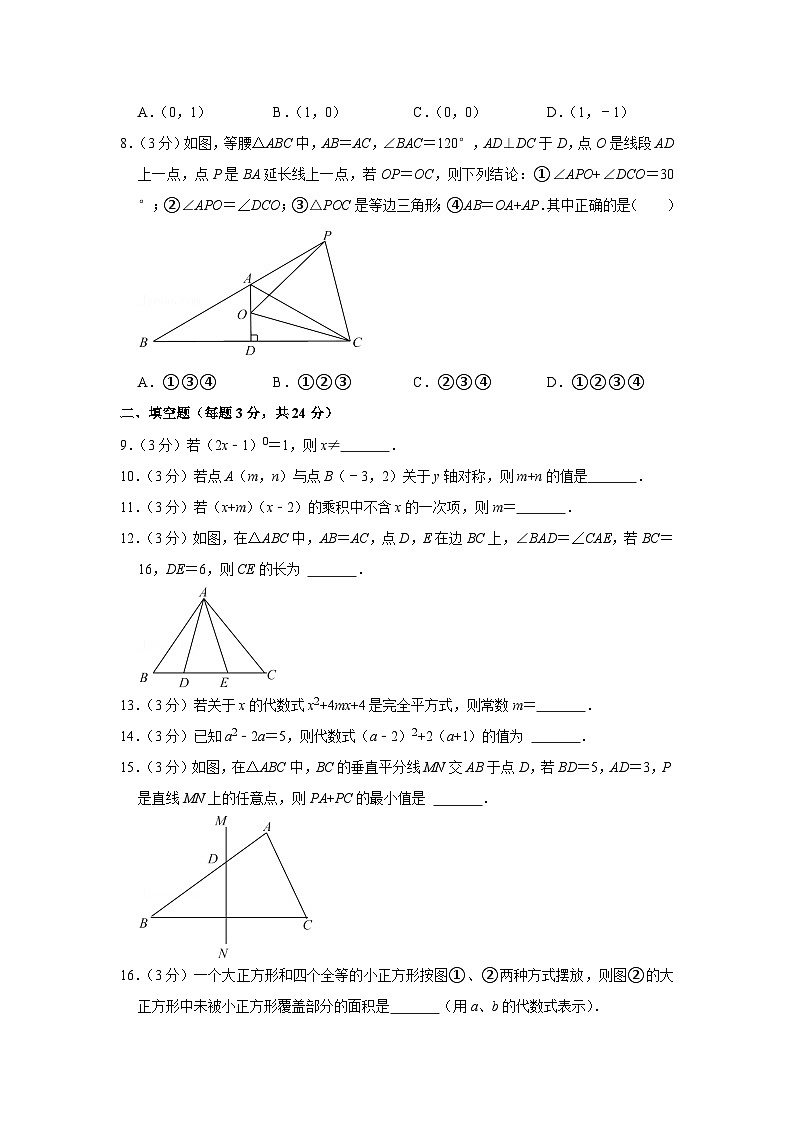
A．（0，1）B．（1，0）C．（0，0）D．（1，﹣1）
8．（3分）如图，等腰△ABC中，AB＝AC，∠BAC＝120°，AD⊥DC于D，点O是线段AD上一点，点P是BA延长线上一点，若OP＝OC，则下列结论：①∠APO+∠DCO＝30°；②∠APO＝∠DCO；③△POC是等边三角形；④AB＝OA+AP．其中正确的是（ ）
A．①③④B．①②③C．②③④D．①②③④
二、填空题（每题3分，共24分）
9．（3分）若（2x﹣1）0＝1，则x≠ ．
10．（3分）若点A（m，n）与点B（﹣3，2）关于y轴对称，则m+n的值是 ．
11．（3分）若（x+m）（x﹣2）的乘积中不含x的一次项，则m＝ ．
12．（3分）如图，在△ABC中，AB＝AC，点D，E在边BC上，∠BAD＝∠CAE，若BC＝16，DE＝6，则CE的长为 ．
13．（3分）若关于x的代数式x2+4mx+4是完全平方式，则常数m＝ ．
14．（3分）已知a2﹣2a＝5，则代数式（a﹣2）2+2（a+1）的值为 ．
15．（3分）如图，在△ABC中，BC的垂直平分线MN交AB于点D，若BD＝5，AD＝3，P是直线MN上的任意点，则PA+PC的最小值是 ．
16．（3分）一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是 （用a、b的代数式表示）．
三、解答题（共52分）
17．（6分）计算：
（1）2x3y•（﹣3xy2）；
（2）[（x+1）（x+2）﹣2]÷x；
（3）（a+b+2c）（a+b﹣2c）．
18．（6分）因式分解：
（1）2a3+6ab；
（2）5x2﹣5y2；
（3）﹣3x2+6xy﹣3y2．
19．（4分）如图，在△ABC中，AB＝AC，D是BC边上的中点，DE⊥AB于点E，DF⊥AC于点F．求证：DE＝DF．
20．（6分）运用所学乘法公式等进行简便运算：
（1）（﹣0.125）11×811；
（2）9.92；
（3）．
21．（4分）已知，求代数式（x﹣1）2+x（x﹣4）+（x+2）（x﹣2）的值．
22．（5分）如图，在2×2的正方形格纸中，△ABC是以格点为顶点的三角形，也称为格点三角形，请你在该正方形格纸中画出与△ABC成轴对称的所有的格点三角形（用阴影表示）．
23．（4分）在等边△ABC中，D为BC上一点，BD＝2CD，DE⊥AB于点E，CE交AD于点P，求∠APE的度数．
24．（6分）阅读下列文字：我们知道，图形是一种重要的数学语言，我国著名的数学家华罗庚先生曾经说“数缺形时少直观，形缺数时难入微”．例如，对于一个图形，通过不同的方法计算图形的面积，就可以得到一个数学等式．
（1）模拟练习：如图，写出一个我们熟悉的数学公式： ；
（2）解决问题：如果a+b＝10，ab＝12，求a2+b2的值；
（3）类比探究：如果一个长方形的长和宽分别为（8﹣x）和（x﹣2），且（8﹣x）2+（x﹣2）2＝20，求这个长方形的面积．
25．（5分）我们规定：若实数a与b的平方差等于80，则称实数对（a，b）在平面直角坐标系中对应的点为“双曲点”；若实数a与b的平方差等于0，则称实数对（a，b）在平面直角坐标系中对应的点为“十字点”．
（1）若P（a，b）为“双曲点”，则a，b应满足的等量关系为 ；
（2）在点A（8，4），B（﹣12，8），C（21，19），D（40，4）中，是“双曲点”的有 ；
（3）若点B（9，k）是“双曲点”，求k的值；
（4）若点A（x，y）为“十字点”，点B（x+5y，5y﹣x）是“双曲点”，求x，y的值．
26．（6分）如图，点C是线段AB上一点，△ACF与△BCE都是等边三角形，连接AE，BF．
（1）求证：AE＝BF；
（2）若点M，N分别是AE，BF的中点，连接CM，MN，NC．
①依题意补全图形；
②判断△CMN的形状，并证明你的结论．
四、附加题：（共20分，每题4分）
27．（4分）已知a＝817，b＝279，c＝913，则a，b，c的大小关系是（ ）
A．a＞b＞cB．a＞c＞bC．a＜b＜cD．b＞c＞a
28．（4分）若实数x满足x2﹣2x﹣1＝0，则2x3﹣2x2﹣6x+2020＝ ．
29．（4分）等腰三角形一腰上的高与另一腰的夹角为54°，则该等腰三角形的底角的度数为 ．
30．（4分）如图，已知∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1＝a，则△A2B2A3的边长为 ，△AnBnAn+1的边长为 ．
31．（4分）如图，在等边△ABC中，点D是边BC上一点，∠BAD＝α（0°＜α＜30°），连接AD．作点C关于直线AD的对称点为E，连接EB并延长交直线AD于点F．
（1）依题意补全图形，直接写出∠AFE的度数；
（2）直接写出线段AF，BF，EF之间的等量关系．
2021-2022学年北京市海淀区清华附中八年级（上）期中数学试卷
参考答案与试题解析
一、选择题（每题3分，共24分）
1．（3分）现实生活中，对称现象无处不在，中国的汉字中有些也具有对称性，下列字是轴对称图形的是（ ）
A．诚B．信C．友D．善
【分析】直接利用轴对称图形的定义得出答案．如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．
【解答】解：“诚”、“信”，“友”都不能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以不是轴对称图形；
“善”能找到这样的一条直线，使图形沿一条直线折叠，直线两旁的部分能够互相重合，所以是轴对称图形；
故选：D．
【点评】此题主要考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．（3分）已知一个正方形边长为a+1，则该正方形的面积为（ ）
A．a2+2a+1B．a2﹣2a+1C．a2+1D．2a+1
【分析】根据正方形的面积公式可求该正方形的面积，再根据完全平方公式计算即可求解．
【解答】解：该正方形的面积为（a+1）2＝a2+2a+1．
故选：A．
【点评】本题主要考查列代数式，解题的关键是熟练掌握正方形的面积公式．
3．（3分）已知等腰三角形两边的长分别为3和7，则此等腰三角形的周长为（ ）
A．10B．15C．17D．19
【分析】等腰三角形两边的长为3和7，具体哪条是底边，哪条是腰没有明确说明，因此要分两种情况讨论．
【解答】解：①当腰是3，底边是7时，3+3＜7，不满足三角形的三边关系，因此舍去．
②当底边是3，腰长是7时，3+7＞7，能构成三角形，则其周长＝3+7+7＝17．
故选：C．
【点评】本题考查了等腰三角形的性质和三角形的三边关系，解题时注意：若没有明确腰和底边，则一定要分类进行讨论，还应验证各种情况是否能构成三角形，这是解题的关键．
4．（3分）下列各式运算结果为a9的是（ ）
A．a6+a3B．a3•a3C．（a3）3D．a18÷a2
【分析】根据合并同类项法则、同底数幂的乘法、幂的乘方、同底数幂的除法法则解决此题．
【解答】解：A．根据合并同类项法则，a6+a3≠a9，那么A不符合题意．
B．根据同底数幂的乘法，a3•a3＝a6，那么B不符合题意．
C．根据幂的乘方，（a3）3＝a9，那么C符合题意．
D．根据同底数幂的除法，a18÷a2＝a16，那么D不符合题意．
故选：C．
【点评】本题主要考查合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法，熟练掌握合并同类项法则、同底数幂的乘法、幂的乘方、同底数幂的除法法则是解决本题的关键．
5．（3分）如图，在△ABC中，AB＝AC，AD、CE分别是△ABC的中线和角平分线．若∠CAD＝20°，则∠ACE的度数是（ ）
A．20°B．35°C．40°D．70°
【分析】根据等腰三角形的性质得到∠BAD＝∠CAD＝20°，∠ABC＝∠ACB，根据三角形内角和定理求出∠ACB，根据角平分线的定义计算即可．
【解答】解：∵AB＝AC，AD是△ABC的中线，
∴∠BAD＝∠CAD＝20°，∠ABC＝∠ACB，
∴∠ACB＝＝70°，
∵CE是△ABC的角平分线，
∴∠ACE＝∠ACB＝35°，
故选：B．
【点评】本题考查的是等腰三角形的性质，三角形的中线和角平分线以及三角形内角和定理，掌握等腰三角形的三线合一是解题的关键．
6．（3分）下列多项式中能用平方差公式分解因式的是（ ）
A．﹣a2﹣b2B．x2+（﹣y）2
C．（﹣x）2+（﹣y）2D．﹣m2+1
【分析】根据平方差公式的结构特征解决此题．
【解答】解：A．根据平方差公式的结构特征，﹣a2﹣b2不能用平方差公式进行因式分解，那么A不符合题意．
B．根据平方差公式的结构特征，x2+（﹣y）2＝x2+y2不能用平方差公式进行因式分解，那么B不符合题意．
C．根据平方差公式的结构特征，（﹣x）2+（﹣y）2＝x2+y2不能用平方差公式进行因式分解，那么C不符合题意．
D．根据平方差公式的结构特征，﹣m2+1＝﹣（m2﹣1）＝﹣（m+1）（m﹣1），﹣m2+1能用平方差公式进行因式分解，那么D符合题意．
故选：D．
【点评】本题主要考查运用公式法进行因式分解，熟练掌握公式法是解决本题的关键．
7．（3分）如图，网格中的每个小正方形边长均为1，△ABC的顶点均落在格点上，若点A的坐标为（﹣2，﹣1），则到△ABC三个顶点距离相等的点的坐标为（ ）
A．（0，1）B．（1，0）C．（0，0）D．（1，﹣1）
【分析】到△ABC三个顶点距离相等的点是AB与AC的垂直平分线的交点，进而得出其坐标．
【解答】解：平面直角坐标系如图所示，AB与AC的垂直平分线的交点为点O，
∴到△ABC三个顶点距离相等的点的坐标为（0，0），
故选：C．
【点评】本题主要考查了线段垂直平分线的性质，线段垂直平分线上任意一点，到线段两端点的距离相等．
8．（3分）如图，等腰△ABC中，AB＝AC，∠BAC＝120°，AD⊥DC于D，点O是线段AD上一点，点P是BA延长线上一点，若OP＝OC，则下列结论：①∠APO+∠DCO＝30°；②∠APO＝∠DCO；③△POC是等边三角形；④AB＝OA+AP．其中正确的是（ ）
A．①③④B．①②③C．②③④D．①②③④
【分析】①利用等边对等角得：∠APO＝∠ABO，∠DCO＝∠DBO，则∠APO+∠DCO＝∠ABO+∠DBO＝∠ABD，据此即可求解；
②因为点O是线段AD上一点，所以BO不一定是∠ABD的角平分线，可作判断；
③证明∠POC＝60°且OP＝OC，即可证得△OPC是等边三角形；
④证明△OPA≌△CPE，则AO＝CE，得AC＝AE+CE＝AO+AP．
【解答】解：①如图1，连接OB，
∵AB＝AC，AD⊥BC，
∴BD＝CD，∠BAD＝∠BAC＝×120°＝60°，
∴OB＝OC，∠ABC＝90°﹣∠BAD＝30°
∵OP＝OC，
∴OB＝OC＝OP，
∴∠APO＝∠ABO，∠DCO＝∠DBO，
∴∠APO+∠DCO＝∠ABO+∠DBO＝∠ABD＝30°，故①正确；
②由①知：∠APO＝∠ABO，∠DCO＝∠DBO，
∵点O是线段AD上一点，
∴∠ABO与∠DBO不一定相等，
则∠APO与∠DCO不一定相等，故②不正确；
③∵∠APC+∠DCP+∠PBC＝180°，
∴∠APC+∠DCP＝150°，
∵∠APO+∠DCO＝30°，
∴∠OPC+∠OCP＝120°，
∴∠POC＝180°﹣（∠OPC+∠OCP）＝60°，
∵OP＝OC，
∴△OPC是等边三角形，故③正确；
④如图2，在AC上截取AE＝PA，
∵∠PAE＝180°﹣∠BAC＝60°，
∴△APE是等边三角形，
∴∠PEA＝∠APE＝60°，PE＝PA，
∴∠APO+∠OPE＝60°，
∵∠OPE+∠CPE＝∠CPO＝60°，
∴∠APO＝∠CPE，
∵OP＝CP，
在△OPA和△CPE中，
，
∴△OPA≌△CPE（SAS），
∴AO＝CE，
∴AC＝AE+CE＝AO+AP，
∴AB＝AO+AP，故④正确；
正确的结论有：①③④，
故选：A．
【点评】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识，正确作出辅助线是解决问题的关键．
二、填空题（每题3分，共24分）
9．（3分）若（2x﹣1）0＝1，则x≠ ．
【分析】直接利用零指数幂的定义得出答案．
【解答】解：∵（2x﹣1）0＝1，
∴2x﹣1≠0，
解得：x≠．
故答案为：．
【点评】此题主要考查了零指数幂，正确掌握相关定义是解题关键．
10．（3分）若点A（m，n）与点B（﹣3，2）关于y轴对称，则m+n的值是 5 ．
【分析】根据关于y轴的对称点的坐标特点：横坐标互为相反数，纵坐标相等，据此求出m、n的值，代入计算可得．
【解答】解：∵点A（m，n）与点B（﹣3，2）关于y轴对称，
∴m＝3、n＝2，
所以m+n＝3+2＝5，
故答案为：5．
【点评】本题主要考查关于x、y轴对称的点的坐标，解题的关键是掌握两点关于y轴对称，纵坐标不变，横坐标互为相反数．
11．（3分）若（x+m）（x﹣2）的乘积中不含x的一次项，则m＝ 2 ．
【分析】根据多项式乘多项式的乘法法则解决此题．
【解答】解：（x+m）（x﹣2）
＝x2﹣2x+mx﹣2m
＝x2+（m﹣2）x﹣2m．
∵（x+m）（x﹣2）的乘积中不含x的一次项，
∴m﹣2＝0．
∴m＝2．
故答案为：2．
【点评】本题主要考查多项式乘多项式，熟练掌握多项式乘多项式的乘法法则是解决本题的关键．
12．（3分）如图，在△ABC中，AB＝AC，点D，E在边BC上，∠BAD＝∠CAE，若BC＝16，DE＝6，则CE的长为 5 ．
【分析】利用等腰三角形的性质和题目的已知条件ASA证得△BAD≌△CAE后即可求得CE的长．
【解答】解：∵AB＝AC，
∴∠B＝∠C，
在△BAD和△CAE中，
，
∴△BAD≌△CAE（ASA），
∴BD＝CE，
∵BC＝16，DE＝6，
∴BD+CE＝10，
∴CE＝5．
故答案为：5．
【点评】本题考查了等腰三角形的性质，解题的关键是利用已知和隐含条件证得三角形全等．
13．（3分）若关于x的代数式x2+4mx+4是完全平方式，则常数m＝ ±1 ．
【分析】根据a2±2ab+b2＝（a±b）2求出m的值．
【解答】解：∵x2±4x+4＝（x±2）2，
∵x2+4mx+4是完全平方式，
∴±4x＝4mx，
∴m＝±1．
故答案为：±1．
【点评】本题考查了完全平方式，掌握a2±2ab+b2＝（a±b）2的熟练应用，两种情况是求m值得关键．
14．（3分）已知a2﹣2a＝5，则代数式（a﹣2）2+2（a+1）的值为 11 ．
【分析】先利用完全平方公式、单项式乘多项式法则化简代数式，再代入求值．
【解答】解：（a﹣2）2+2（a+1）
＝a2﹣4a+4+2a+2
＝a2﹣2a+6．
∵a2﹣2a＝5，
∴原式＝5+6＝11．
故答案为：11．
【点评】本题考查了代数式的化简求值，掌握完全平方公式、单项式乘多项式法则是解决本题的关键．
15．（3分）如图，在△ABC中，BC的垂直平分线MN交AB于点D，若BD＝5，AD＝3，P是直线MN上的任意点，则PA+PC的最小值是 8 ．
【分析】如图，连接PB．利用线段的垂直平分线的性质，可知PC＝PB，推出PA+PC＝PA+PB≥AB，即可解决问题．
【解答】解：如图，连接PB．
∵MN垂直平分线段BC，
∴PC＝PB，
∴PA+PC＝PA+PB，
∵PA+PB≥AB＝BD+DA＝5+3＝8，
∴PA+PC≥8，
∴PA+PC的最小值为8．
故答案为：8．
【点评】本题考查轴对称﹣最短问题，线段的垂直平分线的性质等知识，解题的关键是学会利用两点之间线段最短解决最短问题，属于中考常考题型．
16．（3分）一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是 ab （用a、b的代数式表示）．
【分析】利用大正方形的面积减去4个小正方形的面积即可求解．
【解答】解：设大正方形的边长为x1，小正方形的边长为x2，由图①和②列出方程组得，
解得，
②的大正方形中未被小正方形覆盖部分的面积＝（）2﹣4×（）2＝ab．
故答案为：ab．
【点评】本题考查了平方差公式的几何背景，正确求出大小正方形的边长列代数式，以及整式的化简，正确对整式进行化简是关键．
三、解答题（共52分）
17．（6分）计算：
（1）2x3y•（﹣3xy2）；
（2）[（x+1）（x+2）﹣2]÷x；
（3）（a+b+2c）（a+b﹣2c）．
【分析】（1）根据单项式乘单项式的运算法则进行计算；
（2）先利用多项式乘多项式的运算法则计算乘法，然后算括号里面的，最后再算括号外面的；
（3）将原式进行整理后利用乘法公式进行计算．
【解答】解：原式＝2×（﹣3）x3+1y1+2
＝﹣6x4y3；
（2）原式＝（x2+2x+x+2﹣2）÷x
＝（x2+3x）÷x
＝x+3；
（3）原式＝[（a+b）+2c][（a+b）﹣2c]
＝（a+b）2﹣（2c）2
＝a2+2ab+b2﹣4c2．
【点评】本题考查整式的混合运算，掌握完全平方公式（a±b）2＝a2±2ab+b2和平方差公式（a+b）（a﹣b）＝a2﹣b2的结构是解题关键．
18．（6分）因式分解：
（1）2a3+6ab；
（2）5x2﹣5y2；
（3）﹣3x2+6xy﹣3y2．
【分析】（1）直接提公因式2a即可；
（2）先提公因式，再利用平方差公式即可；
（3）先提公因式，再利用完全平方公式即可．
【解答】解：（1）原式＝2a（a2+3b）；
（2）原式＝5（x2﹣y2）
＝5（x+y）（x﹣y）；
（3）原式＝﹣3（x2﹣2xy+y2）
＝﹣3（x﹣y）2．
【点评】本题考查提公因式法、公式法分解因式，掌握平方差公式、完全平方公式的结构特征是正确应用的前提．
19．（4分）如图，在△ABC中，AB＝AC，D是BC边上的中点，DE⊥AB于点E，DF⊥AC于点F．求证：DE＝DF．
【分析】连接AD，D是BC的中点，那么AD就是等腰三角形ABC底边上的中线，根据等腰三角形三线合一的特性，可知道AD也是∠BAC的角平分线，根据角平分线的点到角两边的距离相等，那么DE＝DF．
【解答】证明：如图，连接AD．
∵AB＝AC，点D是BC边上的中点，
∴AD平分∠BAC，
∵DE、DF分别垂直AB、AC于点E和F．
∴DE＝DF．
【点评】本题考查的是等腰三角形的性质，熟知等腰三角形三线合一的性质是解答此题的关键．
20．（6分）运用所学乘法公式等进行简便运算：
（1）（﹣0.125）11×811；
（2）9.92；
（3）．
【分析】（1）根据积的乘方、有理数的乘方解决此题．
（2）根据完全平方公式解决此题．
（3）根据平方差公式解决此题．
【解答】解：（1）（﹣0.125）11×811
＝
＝
＝（﹣1）11
＝﹣1．
（2）9.92
＝（10﹣0.1）2
＝102﹣2×10×0.1+0.12
＝100﹣2+0.01
＝98.01．
（3）
＝
＝
＝502+1+502﹣1
＝5000．
解法二：原式＝（512+2×51×49+492）＝（51+49）2＝50000．
【点评】本题主要考查积的乘方、有理数的乘方、完全平方公式、平方差公式，熟练掌握积的乘方、有理数的乘方、完全平方公式、平方差公式是解决本题的关键．
21．（4分）已知，求代数式（x﹣1）2+x（x﹣4）+（x+2）（x﹣2）的值．
【分析】先根据完全平方公式，平方差公式，单项式乘多项式进行计算，再合并同类项，最后代入求出答案即可．
【解答】解：（x﹣1）2+x（x﹣4）+（x+2）（x﹣2）
＝x2﹣2x+1+x2﹣4x+x2﹣4
＝3x2﹣6x﹣3，
当x＝﹣时，原式＝3×（﹣）2﹣6×（﹣）﹣3＝+2﹣3＝﹣．
【点评】本题考查了整式的化简与求值，能正确根据整式的运算法则进行化简是解此题的关键，注意运算顺序．
22．（5分）如图，在2×2的正方形格纸中，△ABC是以格点为顶点的三角形，也称为格点三角形，请你在该正方形格纸中画出与△ABC成轴对称的所有的格点三角形（用阴影表示）．
【分析】根据轴对称图形的概念，结合网格作图即可．
【解答】解：如图所示．
【点评】本题主要考查作图—轴对称变换，解题的关键是掌握轴对称变换的概念．
23．（4分）在等边△ABC中，D为BC上一点，BD＝2CD，DE⊥AB于点E，CE交AD于点P，求∠APE的度数．
【分析】如图，根据等边三角形的性质就可以得出∠B＝∠ACB＝60°，BC＝AC，再由直角三角形BED中，30度所对的直角边等于斜边的一半得到BD＝2BE，由BD＝2CD，等量代换得到BE＝CD，利用SAS得到三角形BEC与三角形ADC全等，利用全等三角形对应角相等得到∠BCE＝∠DAC，利用内角和定理及外角性质即可确定出所求角的度数．
【解答】解：如图所示，
∵△ABC为等边三角形，
∴∠ABC＝∠ACB＝60°，AB＝AC＝BC，
∵DE⊥AB，
∴∠DEB＝90°，
在Rt△BDE中，∠BDE＝30°，
∴BD＝2BE，
∵BD＝2DC，
∴BE＝DC，
在△BEC和△CDA中，
，
∴△BEC≌△CDA（SAS），
∴∠BCE＝∠CAD，
∴∠ADC+∠BCE＝∠ADC+∠CAD＝180°﹣∠ACB＝120°，
∵∠APC为△PDC的外角，
∴∠APC＝∠ADC+∠BCE＝120°，
则∠APE＝60°．
【点评】此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
24．（6分）阅读下列文字：我们知道，图形是一种重要的数学语言，我国著名的数学家华罗庚先生曾经说“数缺形时少直观，形缺数时难入微”．例如，对于一个图形，通过不同的方法计算图形的面积，就可以得到一个数学等式．
（1）模拟练习：如图，写出一个我们熟悉的数学公式： （a+b）2＝a2+2ab+b2 ；
（2）解决问题：如果a+b＝10，ab＝12，求a2+b2的值；
（3）类比探究：如果一个长方形的长和宽分别为（8﹣x）和（x﹣2），且（8﹣x）2+（x﹣2）2＝20，求这个长方形的面积．
【分析】（1）根据图形的面积的两种不同计算方法得到完全平方公式；
（2）根据完全平方公式变形即可求解；
（3）根据矩形的周长和面积公式以及完全平方公式即可得到结论．
【解答】解：（1）如图，写出一个我们熟悉的数学公式：（a+b）2＝a2+2ab+b2．
故答案为：（a+b）2＝a2+2ab+b2；
（2）∵a+b＝10，ab＝12，
∴a2+b2＝（a+b）2﹣2ab＝100﹣24＝76；
（3）设8﹣x＝a，x﹣2＝b，
∵长方形的两邻边分别是8﹣x，x﹣2，
∴a+b＝8﹣x+x﹣2＝6，
∵（8﹣x）2+（x﹣2）2＝a2+b2＝（a+b）2﹣2ab＝62﹣2ab＝20，
∴ab＝8，
∴这个长方形的面积＝（8﹣x）（x﹣2）＝ab＝8．
【点评】本题考查了因式分解的应用，完全平方公式，熟练掌握完全平方公式是解题的关键．
25．（5分）我们规定：若实数a与b的平方差等于80，则称实数对（a，b）在平面直角坐标系中对应的点为“双曲点”；若实数a与b的平方差等于0，则称实数对（a，b）在平面直角坐标系中对应的点为“十字点”．
（1）若P（a，b）为“双曲点”，则a，b应满足的等量关系为 a2﹣b2＝80 ；
（2）在点A（8，4），B（﹣12，8），C（21，19），D（40，4）中，是“双曲点”的有 B（﹣12，8），C（21，19） ；
（3）若点B（9，k）是“双曲点”，求k的值；
（4）若点A（x，y）为“十字点”，点B（x+5y，5y﹣x）是“双曲点”，求x，y的值．
【分析】（1）根据题意解决此题．
（2）根据定义判定．
（3）根据“双曲点”定义，列出等式92﹣k2＝80，从而解决此题．
（4）根据“双曲点”、“十字点”定义，列出等式x2﹣y2＝0，（x+5y）2﹣（5y﹣x）2＝80，从而求得x与y．
【解答】解：（1）由题意得：a2﹣b2＝80．
故答案为：a2﹣b2＝80．
（2）∵82﹣42＝48，（﹣12）2﹣82＝80，212﹣192＝（20+1）2﹣（20﹣1）2＝80，402﹣42＝1584，
∴B（﹣12，8），C（21，19）是“双曲点”．
故答案为：B（﹣12，8），C（21，19）．
（3）∵点B（9，k）是“双曲点”，
∴92﹣k2＝80．
∴k2＝1．
∴k＝±1．
（4）∵点A（x，y）为“十字点”，点B（x+5y，5y﹣x）是“双曲点”，
∴x2﹣y2＝0，（x+5y）2﹣（5y﹣x）2＝80．
∴x2﹣y2＝0，xy＝4．
∴x＝y＝±2．
【点评】本题主要考查有理数的乘方、完全平方公式，熟练掌握有理数的乘方、完全平方公式是解决本题的关键．
26．（6分）如图，点C是线段AB上一点，△ACF与△BCE都是等边三角形，连接AE，BF．
（1）求证：AE＝BF；
（2）若点M，N分别是AE，BF的中点，连接CM，MN，NC．
①依题意补全图形；
②判断△CMN的形状，并证明你的结论．
【分析】（1）证明△ACE≌△FCB可得证；
（2）①根据题干要求作图；
②由（1）可得∠CAM＝∠CN，AM＝FN，进而证明△ACM≌△FCN可得证．
【解答】（1）证明：△ACF和△BCE是等边三角形，
∴AC＝CF，∠ACF＝60°，∠BCE＝60°，BC＝CE，
∴∠ACF+∠FCE＝∠BCE+∠FCE，
∴∠ACE＝∠FCB，
∴△ACE≌△FCB（SAS），
∴AE＝BF；
（2）①如图，
②△CMN是等边三角形，理由如下：
由（1）得，
△ACE≌△FCB，AE＝BF，
∴∠CAM＝∠CFN，
∵M、N分别是AE和BF的中点，
∴AM＝AE，FN＝BF，
∴AM＝FN，
∵AC＝CF，
∴△ACM≌△FCN（SAS），
∴CM＝CN，∠ACM＝∠FCN，
∴∠ACM﹣∠FCM＝∠FCN﹣∠FCM，
∴∠MCN＝∠ACF＝60°，
∴△CMN是等边三角形．
【点评】本题考查了等边三角形的性质，全等三角形的判定和性质，解决问题的关键是掌握基础知识及第二问的证明用到第一问的结论．
四、附加题：（共20分，每题4分）
27．（4分）已知a＝817，b＝279，c＝913，则a，b，c的大小关系是（ ）
A．a＞b＞cB．a＞c＞bC．a＜b＜cD．b＞c＞a
【分析】根据幂的乘方、有理数的乘方、有理数的大小关系解决此题．
【解答】解：∵a＝817，b＝279，c＝913，
∴a＝（34）7＝328，b＝（33）9＝327，c＝（32）13＝326．
又∵328＞327＞326，
∴a＞b＞c．
故选：A．
【点评】本题主要考查幂的乘方、有理数的乘方、有理数的大小比较，熟练掌握幂的乘方、有理数的乘方、有理数的大小关系是解决本题的关键．
28．（4分）若实数x满足x2﹣2x﹣1＝0，则2x3﹣2x2﹣6x+2020＝ 2022 ．
【分析】先将x2＝2x+1，x2﹣2x＝1，再代入计算可求解．
【解答】解：∵x2﹣2x﹣1＝0，
∴x2＝2x+1，x2﹣2x＝1，
∴原式＝2x•x2﹣2x2﹣6x+2020
＝2x（2x+1）﹣2x2﹣6x+2020
＝4x2+2x﹣2x2﹣6x+2020
＝2x2﹣4x+2020
＝2（x2﹣2x）+2020
＝2×1+2020
＝2022．
【点评】本题主要考查因式分解的应用，整体代入是解题的关键．
29．（4分）等腰三角形一腰上的高与另一腰的夹角为54°，则该等腰三角形的底角的度数为 72°或18° ．
【分析】在等腰△ABC中，AB＝AC，BD为腰AC上的高，∠ABD＝54°，讨论：当BD在△ABC内部时，如图1，先计算出∠BAD＝36°，再根据等腰三角形的性质和三角形内角和可计算出∠ACB；当BD在△ABC外部时，如图2，先计算出∠BAD＝36°，再根据等腰三角形的性质和三角形外角性质可计算出∠ACB．
【解答】解：在等腰△ABC中，AB＝AC，BD为腰AC上的高，∠ABD＝54°，
当BD在△ABC内部时，如图1，
∵BD为高，
∴∠ADB＝90°，
∴∠BAD＝90°﹣54°＝36°，
∵AB＝AC，
∴∠ABC＝∠ACB＝（180°﹣36°）＝72°；
当BD在△ABC外部时，如图2，
∵BD为高，
∴∠ADB＝90°，
∴∠BAD＝90°﹣54°＝36°，
∵AB＝AC，
∴∠ABC＝∠ACB，
而∠BAD＝∠ABC+∠ACB，
∴∠ACB＝∠BAD＝18°，
综上所述，这个等腰三角形底角的度数为72°或18°．
故答案为：72°或18°．
【点评】本题考查了等腰三角形的性质：等腰三角形的两腰相等；等腰三角形的两个底角相等；等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
30．（4分）如图，已知∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1＝a，则△A2B2A3的边长为 4a ，△AnBnAn+1的边长为 2n﹣1a ．
【分析】利用等边三角形的性质得到∠A1OB1＝∠A1B1O＝30°，OA1＝A1B1＝A2B1＝a，利用同样的方法得到A2O＝A2B2＝2a＝21a，A3B3＝A3O＝2A2O＝4＝22a，利用此规律即可得到AnBn＝2n﹣1a．
【解答】解：∵△A1B1A2为等边三角形，∠MON＝30°，
∴∠A1OB1＝∠A1B1O＝30°，OA1＝A1B1＝A2B1＝a，
同理：A2O＝A2B2＝2＝21a，
A3B3＝A3O＝2A2O＝4a＝22a，
..．
以此类推可得△AnBnAn+1的边长为AnBn＝2n﹣1a．
故答案为：4a；2n﹣1a．
【点评】本题考查规律型：图形的变化类，等边三角形的性质，解题关键是掌握三角形边长的变化规律．
31．（4分）如图，在等边△ABC中，点D是边BC上一点，∠BAD＝α（0°＜α＜30°），连接AD．作点C关于直线AD的对称点为E，连接EB并延长交直线AD于点F．
（1）依题意补全图形，直接写出∠AFE的度数；
（2）直接写出线段AF，BF，EF之间的等量关系．
【分析】（1）根据要求作出图形，利用轴对称的性质，等腰三角形的性质，三角形内角和定理求解即可．
（2）结论：AF＝EF+BF．如图2中，连接CF，在FA上取一点J，使得FJ＝FC，连接CJ，证明△BCF≌△ACJ（SAS），可得结论．
【解答】解：（1）图形如图1所示：
连接AE．
∵△ABC是等边三角形，
∴∠BAC＝60°，AB＝AC，
∵∠BAD＝α，
∴∠CAD＝60°﹣α，
∵E，C关于AD对称，
∴∠DAE＝∠DAC＝60°﹣α，AE＝AC＝AB
∴∠EAB＝60°﹣2α，
∴∠E＝∠ABE＝（180°﹣60°+2α）＝60°+α，
∵∠ABE＝∠AFE+∠BAD，
∴∠AFE＝60°．
（2）结论：AF＝BF+EF．
理由：如图2中，连接CF，在FA上取一点J，使得FJ＝FC，连接CJ
∵E，C关于AF对称，
∴∠AFC＝∠AFE＝60°，EF＝CF，
∵FJ＝FC，
∴△CFJ是等边三角形，
∴CF＝CJ，∠FCJ＝60°，
∵△ABC是等边三角形，
∴∠ACB＝60°，CB＝CA，
∴∠ACB＝∠FCJ，
∴∠BCF＝∠ACJ，
在△BCF和△ACJ中，
，
∴△BCF≌△ACJ（SAS），
∴BF＝AJ，
∴AF＝FJ+AJ＝EF+BF．
【点评】考查了作图﹣轴对称变换，全等三角形的判定和性质，等边三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2022/9/28 17:49:28；用户：笑涵数学；邮箱：15699920825；学号：36906111