



山东省聊城市阳谷县第二实验中学2023-2024学年九年级下学期开学数学试题(原卷版+解析版)
展开1. -的立方根是( )
A. -2B. 4C. -4D. ﹣8
【答案】A
【解析】
【分析】根据平方根的意义可得,然后根据立方根的意义可得到问题解答.
【详解】解:∵,且,
∴的立方根是-2,
故选A .
【点睛】本题考查平方根和立方根综合运用,熟练掌握平方根、立方根的意义和性质是解题关键.
2. 下列运算正确的是( )
A. B. C. D.
【答案】B
【解析】
【分析】根据合并同类项、幂的乘方,同底数幂乘法以及完全平方公式,逐项判断即可.
【详解】A、不是同类项,不能合并,故选项A计算错误;
B、,故选项B计算正确;
C、,故选项C计算错误;
D、,故选项D计算错误.
故选B.
【点睛】本题考查合了并同类项,同底数幂乘法和积的乘方、以及完全平方公式,解题关键是熟记运算法则和公式.
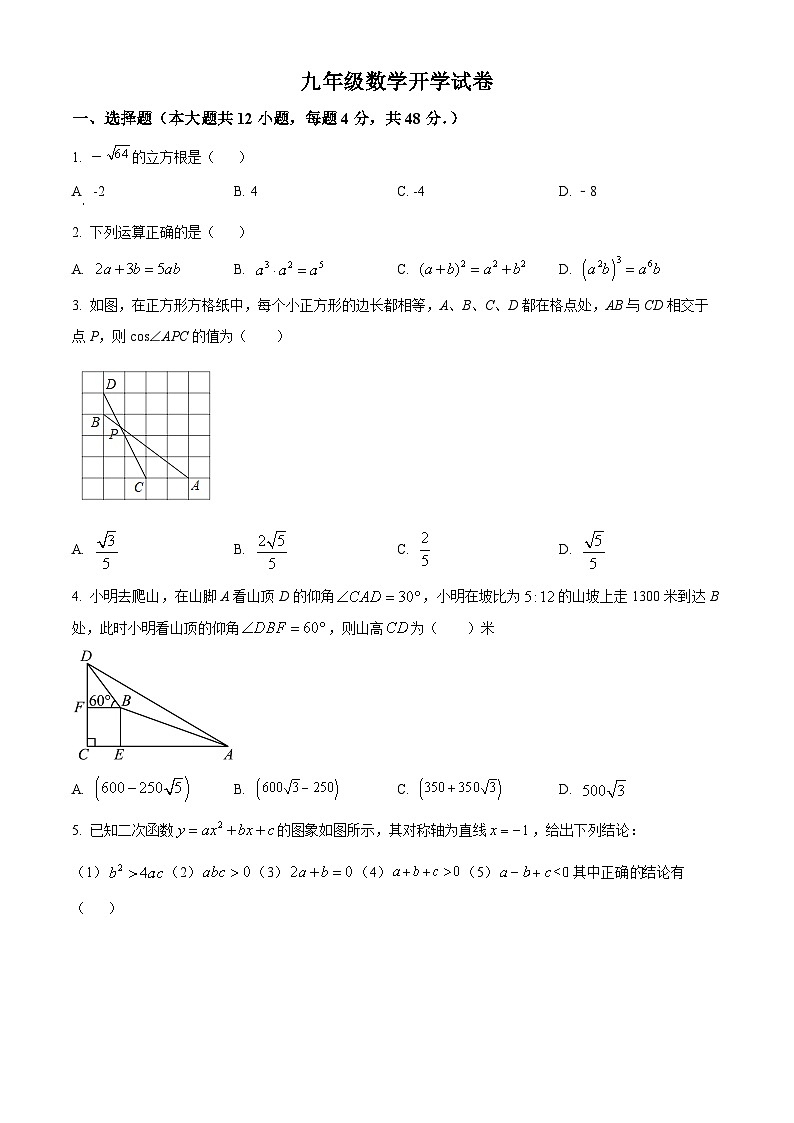
3. 如图,在正方形方格纸中,每个小正方形的边长都相等,A、B、C、D都在格点处,AB与CD相交于点P,则cs∠APC的值为( )
A. B. C. D.
【答案】B
【解析】
【分析】把AB向上平移一个单位到DE,连接CE,则DE∥AB,由勾股定理逆定理可以证明△DCE为直角三角形,所以cs∠APC=cs∠EDC即可得答案.
【详解】解:把AB向上平移一个单位到DE,连接CE,如图.
则DE∥AB,
∴∠APC=∠EDC.
在△DCE中,有,,,
∴,
∴是直角三角形,且,
∴cs∠APC=cs∠EDC=.
故选:B.
【点睛】本题考查了解直角三角形、平行线的性质,勾股定理,作出合适辅助线是解题关键.
4. 小明去爬山,在山脚A看山顶D的仰角,小明在坡比为的山坡上走1300米到达B处,此时小明看山顶的仰角,则山高为( )米
A. B. C. D.
【答案】B
【解析】
【分析】根据,可得,从而得到米,米,设米,则米,由,可得米,再由,可得,从而得到,求出x,即可求解.
【详解】解:∵,,
∴,
∵米,
∴米,米,
设米,则米,
∵,
∴米,
又∵,
∴,
即:,
解得,
∴米,
∴米.
即山高为米.
故选:B
【点睛】本题主要考查了解直角三角形的实际应用,明确题意,准确构造直角三角形是解题的关键.
5. 已知二次函数的图象如图所示,其对称轴为直线,给出下列结论:
(1)(2)(3)(4)(5)其中正确的结论有( )
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】
【分析】根据抛物线与轴交点的各数对(1)进行判断;由抛物线开口方向得到,由抛物线与轴的交点在轴下方得到,由抛物线的对称轴为直线,得到,于是可对(2)进行判断;利用可对(3)进行判断;根据自变量为1时函数值为正数可对(4)进行判断;根据自变量为时函数值为负数可对(5)进行判断.
【详解】解:抛物线与轴有2个交点,
,即,所以(1)正确;
抛物线开口向上,
,
抛物线与轴交于,
,
抛物线的对称轴为直线,
,
,所以(2)错误;
,即,所以(3)错误;
时,,
,所以(4)正确;
时,,
,所以(5)正确.
故选:B.
【点睛】本题考查了二次函数与系数的关系:二次函数,二次项系数决定抛物线的开口方向和大小.当时,抛物线向上开口;当时,抛物线向下开口;一次项系数和二次项系数共同决定对称轴的位置,当与同号时(即,对称轴在轴左;当与异号时(即,对称轴在轴右.(简称:左同右异);常数项决定抛物线与轴交点,抛物线与轴交于.当时,抛物线与轴有2个交点;时,抛物线与轴有1个交点;时,抛物线与轴没有交点.
6. 如图,若是的直径,是的弦,,则( )
A. B. C. D.
【答案】B
【解析】
【分析】由直径所对圆周角为直角即得出,从而由直角三角形两个锐角互余求出,最后由同弧所对圆周角相等即得出.
【详解】解:是的直径,
.
,
又,
.
故选B.
【点睛】本题考查圆周角定理的推论,直角三角形两个锐角互余.掌握直径所对圆周角为直角和同弧所对圆周角相等是解题关键.
7. 如图,点E是的边上的一点,且,连接并延长交的延长线于点F,若,则的周长为( )
A. 21B. 28C. 34D. 42
【答案】C
【解析】
【分析】根据平行四边形的性质和相似三角形的判定和性质解答即可.
【详解】解:∵四边形ABCD是平行四边形,
∴AB∥CF,AB=CD,
∴△ABE∽△DFE,
∴,
∵,
∴AE=6,AB=8,
∴AD=AE+DE=6+3=9,
∴的周长为:(8+9)×2=34.
故选:C.
【点睛】此题考查相似三角形的判定和性质,关键是根据平行四边形的性质和相似三角形的判定和性质解答.
8. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )
A. m<2B. m≤2C. m<2且m≠1D. m≤2且m≠1
【答案】D
【解析】
【分析】根据二次项系数非零及根的判别式△≥0,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围.
【详解】解:因为关于x的一元二次方程x2-2x+m=0有实数根,所以b2-4ac=22-4(m-1)×1≥0,解得m≤2.又因为(m-1)x2+2x+1=0是一元二次方程,所以m-1≠0.综合知,m的取值范围是m≤2且m≠1,因此本题选D.
【点睛】本题考查了根的判别式以及一元二次方程的定义,根据二次项系数非零及根的判别式△≥0,找出关于m的一元一次不等式组是解题的关键.
9. 将抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为( )
A y=3(x+2)2﹣1B. y=3(x﹣2)2+1C. y=3(x﹣2)2﹣1D. y=3(x+2)2+1
【答案】A
【解析】
【详解】函数图象的平移法则为:左加右减,上加下减;根据这个平移法则,抛物线y=3x2向左平移2个单位,再向下平移1个单位,所得抛物线为y=3(x+2)2﹣1.故选A.
考点:二次函数图象的平移法则.
10. 若不等式组无解,则的取值范围为( )
A. B. C. D.
【答案】A
【解析】
【分析】求出第一个不等式的解集,根据口诀:大大小小找不到可得关于m的不等式,解之可得.
【详解】解不等式,得:x>8,
∵不等式组无解,
∴4m≤8,
解得m≤2,
故选A.
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
11. 在△ABC中,DE∥BC,若AD=1,DB=2,则的值为( )
A. B. C. D. 23
【答案】B
【解析】
【详解】解:∵AD=1,DB=2,
∴AB=AD+BD=1+2=3,
∵DE∥BC,
∴△ADE∽△ABC,
∴DE:BC=AD:AB=1:3.
故选B.
12. 求1+2+22+23+…+22020的值,可令S=1+2+22+23+…+22020,则2S=2+22+23+24+…+22021,因此2S-S=22021-1.仿照以上推理,计算出1+2020+20202+20203+…+20202020的值为( )
A. B. C. D.
【答案】C
【解析】
【分析】由题意可知S= 1+2020+20202+20203+…+20202020①,可得到2020S=2020+20202+20203+…+20202020+20202021②,然后由②-①,就可求出S的值.
【详解】解:设S= 1+2020+20202+20203+…+20202020①
则2020S=2020+20202+20203+…+20202020+20202021②
由②-①得:
2019S=20202021-1
∴.
故答案为:C.
【点晴】本题主要考查探索数与式的规律,有理数的加减混合运算.
二、填空题(本大题共6小题,共24分.只要求填写最后结果,每小题填对得4分.)
13. 因式分解:____________.
【答案】
【解析】
【分析】本题考查因式分解.先提公因式后,再用平方差公式进行分解即可.
【详解】解:
.
故答案为:.
14. 若,则的取值范围是__________.
【答案】
【解析】
【分析】等式左边为算术平方根,结果为非负数,即1-x≥0.
【详解】解:由于二次根式的结果为非负数可知,
1-x≥0,解得x≤1,
故答案为:.
【点睛】本题利用了二次根式的结果为非负数求x的取值范围.
15. 如图,分别与相切于两点,且.若点是上异于点的一点,则的大小为___________.
【答案】或
【解析】
【分析】根据切线的性质得到,根据四边形内角和为,得出,然后根据圆周角定理即可求解.
【详解】解:如图所示,连接,当点在优弧上时,
∵分别与相切于两点
∴,
∵.
∴
∵,
∴,
当点在上时,
∵四边形是圆内接四边形,
∴,
故答案为:或.
【点睛】本题考查了切线的性质,圆周角定理,多边形内角和,熟练掌握切线的性质与圆周角定理是解题的关键.
16. 若二次函数的图象与轴有交点,则的取值范围是___________.
【答案】且
【解析】
【分析】根据题意可得关于x的一元二次方程有实数根,据此利用判别式和一元二次方程的定义进行求解即可.
【详解】解:∵二次函数的图象与轴有交点,
∴关于x的一元二次方程有实数根,
∴,
∴且,
故答案为:且.
【点睛】本题主要考查了二次函数与一元二次方程的关系,熟知二次函数与x轴有交点即对应的一元二次方程有实数根是解题的关键.
17. 若关于x的分式方程有增根,则____.
【答案】3
【解析】
【分析】本题考查了解分式方程 ,利用增根求字母的值,增根就是使最简公分母为零的未知数的值;解决此类问题的步骤:①化分式方程为整式方程;②让最简公分母等于零求出增根的值;③把增根代入到整式方程中即可求得相关字母的值.
先把分式方程去分母转化为整式方程,然后由分式方程有增根求出x的值,代入到转化以后的整式方程中计算即可求出m的值.
【详解】解:去分母得:,整理得:,
∵关于x的分式方程有增根,即,
∴,
把代入到中得:,
解得:;
故答案为:3.
18. 如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把三角形AE折叠,使点D恰好落在BC边上,设此点为F,若三角形ABF的面积为24,那么CE长度为__________cm.
【答案】
【解析】
【分析】由折叠可得∠D=∠AFE=90°,结合已知条件不难证明△ABF∽△FCE,由三角形相似的性质可以得出EC与CF的比值,根据比值分别设出EC、CF的长度,进而表示出EF、DE的长度,列方程解出x,进而求出CE的长度.
【详解】∵矩形ABCD,
∴AB=CD=6cm,∠B=∠C=∠D=90°,
∵S△ABF=AB·BF=×6BF=24,
∴BF=8,
由折叠可得∠AFE=∠D=90°,DE=EF,
∴∠AFB+∠EFC=90°,
∵∠AFB+∠BAF=90°,
∴∠EFC=∠BAF,
∵△ABF与△FCE中,
,
∴△ABF∽△FCE,
∴=,
∴=43,
设CE=4xcm,CF=3xcm,则EF=ED=5xcm,
∴6=5x+4x,
∴x=23,
∴CE=cm.
故答案为.
【点睛】本题主要考查相似三角形的判定与性质以及勾股定理的应用.
三、解答题(本大题共8小题,共78分.)
19. (1)先化简,再求代数式的值,其中.
(2)解不等式组:,并把解集表示在数轴上.
【答案】(1),;(2),数轴表示见解析
【解析】
【分析】本题主要考查了分式的化简求值,解一元一次不等式组,在数轴上表示不等式组的解集,求特殊角三角函数值:
(1)先把小括号内的式子通分,再把除法变成乘法后约分化简,接着计算出x的值,最后代值计算即可;
(2)先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集,再在数轴上表示出不等式组的解集即可.
【详解】解:(1)
,
∵,
∴原式;
(2)
解不等式①得:,
解不等式②得:,
∴不等式组的解集为
数轴表示如下所示:
20. 某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥的长度.
【答案】
【解析】
【分析】过C地点作交AB于D点,根据桥两端A,B两点的俯角分别为60°和45°,可得,,利用特殊角懂得三角函数求解即可.
【详解】解:如图示:过C地点作交AB于D点,
则有:,,
∴,
,
∴.
【点睛】本题考查了特殊角的三角函数的运算,熟悉特殊角的三角函数值是解题的关键.
21. 2024年哈尔滨冰雪旅游火爆全国,吸引了大量游客前来旅游.“当好东道主,热情迎嘉宾”,哈尔滨某知名小吃店计划购买A,B两种食材制作小吃.已知购买1千克A种食材和1千克B种食材共需68元,购买5千克A种食材和3千克B种食材共需280元.
(1)求A,B两种食材的单价;
(2)该小吃店计划购买两种食材共36千克,其中购买A种食材千克数不少于B种食材千克数的2倍,当A,B两种食材分别购买多少千克时,总费用最少?并求出最少总费用.
【答案】(1)A种食材的单价为38元,B种食材的单价为30元
(2)当A,B两种食材分别购买24,12千克时,总费用最少为1272元
【解析】
【分析】本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用,根据题意列出方程组,不等式以及一次函数关系式是解题的关键.
(1)设A种食材的单价为a元,B种食材的单价为b元,根据题意列出二元一次方程组,解方程组即可求解;
(2)设A种食材购买x千克,则B种食材购买千克,根据题意列出不等式,得出,进而设总费用为y元,根据题意,,根据一次函数的性质即可求解.
【小问1详解】
解:设A种食材的单价为a元,B种食材的单价为b元,
根据题意得,,
解得:,
答:A种食材的单价为38元,B种食材的单价为30元;
【小问2详解】
解:设A种食材购买x千克,则B种食材购买千克,
根据题意,,
解得:,
设总费用为y元,根据题意,,
∵,y随x的增大而增大,
∴当时,y最小,
∴最少总费用为(元),
答:当A,B两种食材分别购买24,12千克时,总费用最少为1272元.
22. 如图,为的直径,射线交于点F,点C为劣弧的中点,过点C作,垂足为E,连接.
(1)求证:是的切线;
(2)若,求阴影部分的面积.
【答案】(1)证明见解析;(2).
【解析】
【分析】(1)连接BF,证明BF//CE,连接OC,证明OC⊥CE即可得到结论;
(2)连接OF,求出扇形FOC的面积即可得到阴影部分的面积.
【详解】(1)连接,
是的直径,
,即,
,
连接,
∵点C为劣弧的中点,
,
∵,
∵OC是的半径,
∴CE是的切线;
(2)连接
,,
∵点C为劣弧的中点,
,
,
,
,
∴S扇形FOC=,
即阴影部分的面积为:.
【点睛】本题主要考查了切线的判定以及扇形面积的求法,熟练掌握切线的判定定理以及扇形面积的求法是解答此题的关键.
23. 如图,在平面直角坐标系中,一次函数与反比例函数交于,两点,与y轴交于点C,连接,.
(1)求反比例函数和一次函数的表达式;
(2)求的面积;
(3)请根据图象直接写出不等式的解集.
【答案】(1),;
(2)9; (3)或.
【解析】
【分析】(1)把点B代入反比例函数,即可得到反比例函数的解析式;把点A代入反比例函数,即可求得点A的坐标;把点A、B的坐标代入一次函数一次函数即可求得a、b的值,从而得到一次函数的解析式;
(2)的面积是和的面积之和,利用面积公式求解即可;
(3)利用图象,找到反比例函数图象在一次函数图象下方所对应的x的范围,直接得出结论.
【小问1详解】
∵点在反比例函数的图象上,
∴,
解得:
∴反比例函数的表达式为.
∵在反比例函数的图象上,
∴,
解得,(舍去).
∴点A的坐标为.
∵点A,B在一次函数的图象上,
把点,分别代入,得,
解得,
∴一次函数的表达式为;
【小问2详解】
∵点C为直线AB与y轴的交点,
∴把代入函数,得
∴点C坐标为
∴,
∴
.
【小问3详解】
由图象可得,不等式的解集是或.
【点睛】此题是反比例函数与一次函数的交点问题,考查了待定系数法求函数的解析式,三角形面积,函数与不等式的关系,求出两个函数解析式是解本题的关键.
24. 某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示.
(1)求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)设每月获得的利润为W(元).这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?
【答案】(1)y=﹣10x+1000
(2)销售单价定为70元时,每月的销售利润最大,最大利润是9000元
【解析】
【分析】(1)根据题意用待定系数法求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)根据利润=单件利润×销量列出函数解析式,根据函数的性质求最值.
【小问1详解】
设y与x之间的函数关系式为:y=kx+b(k≠0),
将(40,600),(80,200)代入得:,
解得:,
∴y与x之间的函数关系式为y=﹣10x+1000;
【小问2详解】
由题意得:W=(x﹣40)y=(x﹣40)(﹣10x+1000)=﹣10x2+1400x﹣40000,
配方得:W=﹣10(x﹣70)2+9000,
∵a=﹣10<0,
∴当x=70时,W有最大值为9000,
答:这种文化衫销售单价定为70元时,每月的销售利润最大,最大利润是9000元.
【点睛】本题考查二次函数的应用以及待定系数法求函数解析式,关键是列出函数关系式.
浙江省宁波市鄞州第二实验中学2023-2024学年九年级下学期开学考数学试题(原卷版+解析版): 这是一份浙江省宁波市鄞州第二实验中学2023-2024学年九年级下学期开学考数学试题(原卷版+解析版),文件包含浙江省宁波市鄞州第二实验中学2023-2024学年九年级下学期开学考数学试题原卷版docx、浙江省宁波市鄞州第二实验中学2023-2024学年九年级下学期开学考数学试题解析版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
2024年山东省聊城市阳谷县九年级中考二模数学试题(原卷版+解析版): 这是一份2024年山东省聊城市阳谷县九年级中考二模数学试题(原卷版+解析版),文件包含2024年山东省聊城市阳谷县九年级中考二模数学试题原卷版docx、2024年山东省聊城市阳谷县九年级中考二模数学试题解析版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
山东省聊城市阳谷县2023-2024学年七年级下学期期中数学试题(原卷版+解析版): 这是一份山东省聊城市阳谷县2023-2024学年七年级下学期期中数学试题(原卷版+解析版),文件包含山东省聊城市阳谷县2023-2024学年七年级下学期期中数学试题原卷版docx、山东省聊城市阳谷县2023-2024学年七年级下学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












