高教版（2021）拓展模块二 下册8.1.2 分步计数原理评优课课件ppt

这是一份高教版（2021）拓展模块二 下册8.1.2 分步计数原理评优课课件ppt，共9页。PPT课件主要包含了情境导入，探索新知，分步计数原理，典型例题，巩固练习，归纳总结，布置作业等内容，欢迎下载使用。

某校拟从3名男生、6名女生中，各推选1名参加全国职业院校技能大赛某一赛项的市级选拔赛，问共有多少种不同的选法？
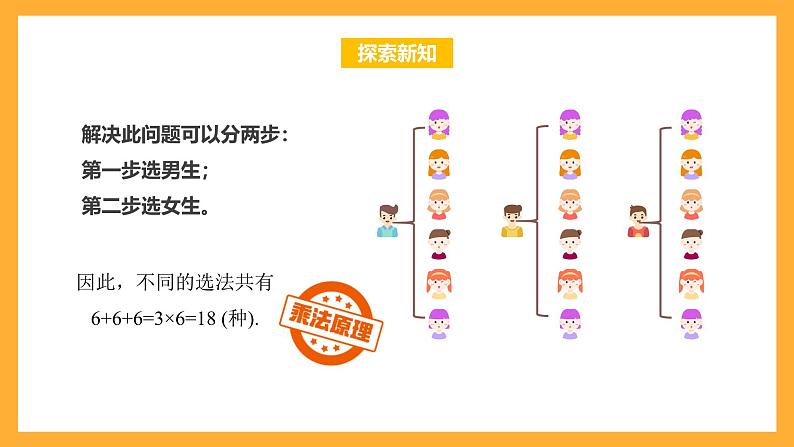
解决此问题可以分两步：第一步选男生；第二步选女生。
因此，不同的选法共有  6+6+6=3×6=18 (种). 
一般地，如果完成一件事有n个步骤. 完成第一个步骤有k1种方法，完成第2个步骤有k2种方法，⋯ ⋯ ，完成第n个步骤有kn种方法，并且只有这n个步骤都完成后，这件事才能完成，那么完成这件事的方法共有 N= k1k2 ⋯ kn (种). 上面的计数原理称为分步计数原理.分类计数原理又称乘法原理.
例2 书架的第一层有6本不同的数学书，第二层有7本不同的语文书，第三层有5本不同的英语书. 若从这些书中取1本数学书、1本语文书和1本英语书，共有多少种不同的取法？
1.小明到黄山游览，他计划先从某市乘坐火车到合肥，第二天再从合肥乘坐汽车到黄山.一天中从该市到合肥适合乘坐的火车有10个班次，从合肥到黄山适合乘坐 的汽车有10个班次，那么小明从该市到黄山有多少种不同的乘车方案？  2.某班甲、乙、丙、丁4 名同学报名参加学校的兵乓球、羽毛球、网球三项不同的 比赛，每人只能报名参加一项比赛，且每项比赛只允许1人报名参加，问共有多少种不同的参赛方案？
1.分步计数原理的概念2.分步计数原理的特点
书面作业：完成下列题目
1.某教学大楼共有四层，每层均有两个楼梯，由一层到四层的走法共有__________种.2.用1,2,3,4这四个数字可以组成_______个没有重复数字的三位数.