新高考数学一轮复习教案第8章第6节 抛物线（含解析）

这是一份新高考数学一轮复习教案第8章第6节 抛物线（含解析），共19页。
1.结合抛物线的定义，考查求抛物线方程、最值等问题，凸显直观想象的核心素养．
2．结合抛物线的几何性质及几何图形，求其相关性质及性质的应用能力，凸显数学运算、直观想象的核心素养．
[理清主干知识]
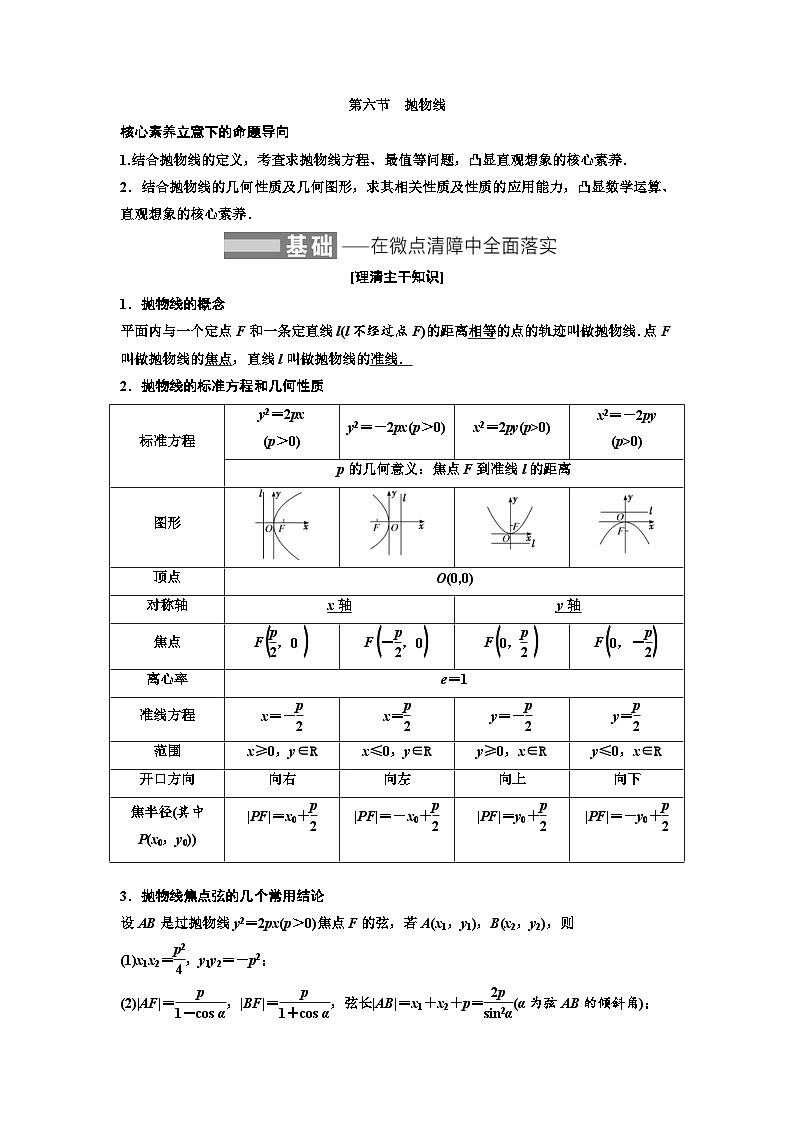
1．抛物线的概念
平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．
2．抛物线的标准方程和几何性质
3．抛物线焦点弦的几个常用结论
设AB是过抛物线y2＝2px(p＞0)焦点F的弦，若A(x1，y1)，B(x2，y2)，则
(1)x1x2＝eq \f(p2,4)，y1y2＝－p2；
(2)|AF|＝eq \f(p,1－cs α)，|BF|＝eq \f(p,1＋cs α)，弦长|AB|＝x1＋x2＋p＝eq \f(2p,sin2α)(α为弦AB的倾斜角)；
(3)eq \f(1,|FA|)＋eq \f(1,|FB|)＝eq \f(2,p)；
(4)以弦AB为直径的圆与准线相切；
(5)焦点弦端点与顶点构成的三角形面积：
S△AOB＝eq \f(p2,2sin θ)＝eq \f(1,2)|AB||d|＝eq \f(1,2)|OF|·|y1－y2|；
(6)通径：过焦点垂直于对称轴的弦，长等于2p，通径是过焦点最短的弦；
(7)以AF或BF为直径的圆与y轴相切；
(8)过焦点弦的端点的切线互相垂直且交点在准线上．
[澄清盲点误点]
一、关键点练明
1．(抛物线的标准方程)已知抛物线C与双曲线x2－y2＝1有相同的焦点，且顶点在原点，则抛物线C的方程是( )
A．y2＝±2eq \r(2)x B．y2＝±2x
C．y2＝±4x D．y2＝±4eq \r(2)x
解析：选D 由已知知双曲线的焦点为(－eq \r(2)，0)，(eq \r(2)，0)．设抛物线方程为y2＝±2px(p>0)，则eq \f(p,2)＝eq \r(2)，所以p＝2eq \r(2)，所以抛物线方程为y2＝±4eq \r(2)x.故选D.
2．(抛物线的定义)若抛物线y＝4x2上的一点M到焦点的距离为1，则点M的纵坐标是( )
A.eq \f(17,16) B．eq \f(15,16)
C.eq \f(7,8) D．0
解析：选B M到准线的距离等于M到焦点的距离，又准线方程为y＝－eq \f(1,16)，设M(x，y)，则y＋eq \f(1,16)＝1，∴y＝eq \f(15,16).
3．(抛物线的性质)若抛物线y2＝2px(p>0)的焦点是椭圆eq \f(x2,3p)＋eq \f(y2,p)＝1的一个焦点，则p＝( )
A．2 B．3
C．4 D．8
解析：选D 抛物线y2＝2px(p>0)的焦点坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))，椭圆eq \f(x2,3p)＋eq \f(y2,p)＝1的焦点坐标为(±eq \r(2p)，0)．
由题意得eq \f(p,2)＝eq \r(2p)，解得p＝0(舍去)或p＝8.
二、易错点练清
1．(忽视抛物线的标准形式)抛物线y＝－2x2的准线方程是( )
A．x＝eq \f(1,2) B．x＝eq \f(1,8)
C．y＝eq \f(1,2) D．y＝eq \f(1,8)
解析：选D 抛物线方程为x2＝－eq \f(1,2)y，所以p＝eq \f(1,4)，准线方程为y＝eq \f(1,8).
2．(忽视抛物线的开口方向)过点P(－2,3)的抛物线的标准方程是( )
A．y2＝－eq \f(9,2)x或x2＝eq \f(4,3)y B．y2＝eq \f(9,2)x或x2＝eq \f(4,3)y
C．y2＝eq \f(9,2)x或x2＝－eq \f(4,3)y D．y2＝－eq \f(9,2)x或x2＝－eq \f(4,3)y
解析：选A 设抛物线的标准方程为y2＝kx或x2＝my，代入点P(－2,3)，解得k＝－eq \f(9,2)，m＝eq \f(4,3)，所以y2＝－eq \f(9,2)x或x2＝eq \f(4,3)y.故选A.
3．(忽视焦点的位置)若抛物线的焦点在直线x－2y－4＝0上，则此抛物线的标准方程为______________．
解析：令x＝0，得y＝－2；令y＝0，得x＝4.所以抛物线的焦点是(4,0)或(0，－2)，故所求抛物线的标准方程为y2＝16x或x2＝－8y.
答案：y2＝16x或x2＝－8y
考点一 抛物线的定义及应用
[典例] (1)(2020·全国卷Ⅰ)已知A为抛物线C：y2＝2px(p＞0)上一点，点A到C的焦点的距离为12，到y轴的距离为9，则p＝( )
A．2 B．3
C．6 D．9
(2)已知抛物线y2＝2x的焦点是F，点P是抛物线上的动点，若A(3,2)，则|PA|＋|PF|的最小值为________，此时点P的坐标为________．
[解析] (1)根据抛物线的定义及题意得，点A到C的准线x＝－eq \f(p,2)的距离为12，因为点A到y轴的距离为9，所以eq \f(p,2)＝12－9，解得p＝6.故选C.
(2)将x＝3代入抛物线方程
y2＝2x，得y＝±eq \r(6).
因为eq \r(6)＞2，所以点A在抛物线内部，如图所示．过点P作PQ⊥l于点Q，
则|PA|＋|PF|＝|PA|＋|PQ|(运用定义进行转化)，
当PA⊥l，即A，P，Q三点共线时，
|PA|＋|PQ|最小(两点之间，线段最短)，
最小值为eq \f(7,2)，即|PA|＋|PF|的最小值为eq \f(7,2)，此时点P的纵坐标为2，代入y2＝2x，得x＝2，所以所求点P的坐标为(2,2)．
[答案] (1)C (2)eq \f(7,2) (2,2)
[方法技巧]
1．利用抛物线的定义可解决的常见问题
2．抛物线定义的应用规律
[提醒] 建立函数关系后，一定要根据题目的条件探求自变量的取值范围，即函数的定义域．
[针对训练]
1．若点A为抛物线y2＝4x上一点，F是抛物线的焦点，|AF|＝5，点P为直线x＝－1上的动点，则|PA|＋|PF|的最小值为( )
A．8 B．2eq \r(13)
C．2＋eq \r(41) D．eq \r(65)
解析：选D 由题意可知，p＝2，F(1,0)，由抛物线的定义可知，|AF|＝xA＋eq \f(p,2)＝xA＋1＝5，∴xA＝4，代入抛物线方程，得yeq \\al(2,A)＝16，不妨取点A为(4,4)．如图，设点F关于x＝－1的对称点为E，则E(－3,0)，∴|PA|＋|PF|＝|PA|＋|PE|≥|AE|＝eq \r(4＋32＋42)＝eq \r(65).
2．如图，圆锥底面半径为eq \r(2)，体积为eq \f(2\r(2),3)π，AB，CD是底面圆O的两条互相垂直的直径，E是母线PB的中点，已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分，则该抛物线的焦点到其准线的距离等于________．
解析：由V＝eq \f(1,3)πr2h＝eq \f(1,3)π×(eq \r(2))2×PO＝eq \f(2\r(2),3)π，得PO＝eq \r(2)，则PB＝2，OE＝1，OC＝OD＝eq \r(2).
以E为坐标原点，OE为x轴，过E点与CD平行的直线为y轴建立如图所示的平面直角坐标系，则C(－1，eq \r(2))．
设抛物线的方程为y2＝－2px(p>0)，
∴(eq \r(2))2＝－2p×(－1)，解得p＝1，
故焦点到其准线的距离等于1.
答案：1
考点二 抛物线的标准方程
[典例] (1)已知抛物线y2＝ax上的点M(1，m)到其焦点的距离为2，则该抛物线的标准方程为( )
A．y2＝2x B．y2＝4x
C．y2＝3x D．y2＝5x
(2)设抛物线C：y2＝2px(p>0)的焦点为F，点M在C上，|MF|＝5.若以MF为直径的圆过点A(0,2)，则C的方程为( )
A．y2＝4x或y2＝8x B．y2＝2x或y2＝8x
C．y2＝4x或y2＝16x D．y2＝2x或y2＝16x
[解析] (1)由题得点Meq \b\lc\(\rc\)(\a\vs4\al\c1(1，m))到准线的距离为2，
所以1＋eq \f(a,4)＝2，解得a＝4.
所以该抛物线的标准方程为y2＝4x.
(2)由已知得抛物线的焦点Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))设点M(x0，y0)，
则AF―→＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，－2))，AM―→＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(y\\al(2,0),2p)，y0－2)).
由已知得，AF―→·AM―→＝0，即yeq \\al(2,0)－8y0＋16＝0，
因而y0＝4，Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(8,p)，4)).
由|MF|＝5，得 eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(8,p)－\f(p,2)))2＋16)＝5.
又p>0，解得p＝2或p＝8.
故C的方程为y2＝4x或y2＝16x.
[答案] (1)B (2)C
[方法技巧]
抛物线的标准方程的求法
(1)定义法
根据抛物线的定义，确定p的值(系数p是指焦点到准线的距离)，再结合焦点位置，求出抛物线方程．标准方程有四种形式，要注意选择．
(2)待定系数法
①根据抛物线焦点是在x轴上还是在y轴上，设出相应形式的标准方程，然后根据条件确定关于p的方程，解出p，从而写出抛物线的标准方程；
②当焦点位置不确定时，有两种方法解决．一种是分情况讨论，注意要对四种形式的标准方程进行讨论，对于焦点在x轴上的抛物线，若开口方向不确定需分为y2＝－2px(p>0)和y2＝2px(p>0)两种情况求解．另一种是设成y2＝mx(m≠0)，若m>0，开口向右；若m0)的焦点F的直线l交抛物线于点A，B，交其准线于点C，若|BC|＝2|BF|，且|AF|＝3，则此抛物线的方程为( )
A．y2＝9x B．y2＝6x
C．y2＝3x D．y2＝eq \r(3)x
解析：选C 如图，过点A，B分别作准线的垂线，交准线于点E，D，设|BF|＝a，则由已知得|BC|＝2a，由抛物线定义得|BD|＝a，故∠BCD＝30°，在直角三角形ACE中，因为|AE|＝|AF|＝3，|AC|＝3＋3a，2|AE|＝|AC|，所以3＋3a＝6，从而得a＝1，|FC|＝3a＝3，
所以p＝|FG|＝eq \f(1,2)|FC|＝eq \f(3,2)，因此抛物线的方程为y2＝3x，故选C.
2．已知抛物线x2＝2py(p>0)的焦点为F，点P为抛物线上的动点，点M为其准线上的动点，若△FPM为边长是4的等边三角形，则此抛物线的方程为________．
解析：△FPM为等边三角形，则|PM|＝|PF|，由抛物线的定义得PM垂直于抛物线的准线，设Peq \b\lc\(\rc\)(\a\vs4\al\c1(m，\f(m2,2p)))，则点Meq \b\lc\(\rc\)(\a\vs4\al\c1(m，－\f(p,2))).因为焦点Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(p,2)))，△FPM是等边三角形，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(m2,2p)＋\f(p,2)＝4，,\a\vs4\al( \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)＋\f(p,2)))2＋m2))＝4，))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(m2＝12，,p＝2，))因此抛物线方程为x2＝4y.
答案：x2＝4y
考点三 抛物线的几何性质
[典例] (1)(2020·全国卷Ⅲ)设O为坐标原点，直线x＝2与抛物线C：y2＝2px(p>0)交于D，E两点，若OD⊥OE，则C的焦点坐标为( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4)，0)) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，0))
C．(1,0) D．(2,0)
(2)已知F是抛物线C：y2＝8x的焦点，M是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则|FN|＝________.
[解析] (1)将直线方程与抛物线方程联立，可得y＝±2eq \r(p)，不妨设D(2,2eq \r(p))，E(2， －2eq \r(p))．
由OD⊥OE，可得OD―→·OE―→＝4－4p＝0，解得p＝1，
所以抛物线C的方程为y2＝2x，其焦点坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，0)).
(2)依题意，抛物线C：y2＝8x的焦点F(2,0)，因为M是C上一点，FM的延长线交y轴于点N，M为FN的中点，设M(a，b)(b>0)，所以a＝1，b＝2eq \r(2)，所以N(0,4eq \r(2))，|FN|＝eq \r(4＋32)＝6.
[答案] (1)B (2)6
[方法技巧]
抛物线几何性质的应用技巧
(1)涉及抛物线几何性质的问题常结合图形思考，通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征，体现了数形结合思想解题的直观性．
(2)与抛物线的焦点弦长有关的问题，可直接应用公式求解．解题时，需依据抛物线的标准方程，确定弦长公式是由交点横坐标还是由交点纵坐标定，是p与交点横(纵)坐标的和还是与交点横(纵)坐标的差，这是正确解题的关键．
[针对训练]
1．过抛物线y2＝4x的焦点F的直线交该抛物线于A，B两点，O为坐标原点．若|AF|＝3，则△AOB的面积为( )
A.eq \f(\r(2),2) B．eq \r(2)
C.eq \f(3\r(2),2) D．2eq \r(2)
解析：选C 由题意设A(x1，y1)，B(x2，y2)(y1>0，y20)的焦点为F，M是抛物线C上的一点，若△OFM的外接圆与抛物线C的准线相切，且该圆的面积为36π，则p＝( )
A．2 B．4
C．6 D．8
解析：选D 依题意，△OFM的外接圆半径为6，△OFM的外接圆圆心应位于OF的垂直平分线x＝eq \f(p,4)上，圆心到准线x＝－eq \f(p,2)的距离为6，即eq \f(p,4)＋eq \f(p,2)＝6，解得p＝8，故选D.
4．若直线AB与抛物线y2＝4x交于A，B两点，且AB⊥x轴，|AB|＝4eq \r(2)，则抛物线的焦点到直线AB的距离为( )
A．1 B．2
C．3 D．5
解析：选A 由|AB|＝4eq \r(2)及AB⊥x轴，不妨设点A的纵坐标为2eq \r(2)，代入y2＝4x得点A的横坐标为2，从而直线AB的方程为x＝2.又y2＝4x的焦点为(1,0)，所以抛物线的焦点到直线AB的距离为2－1＝1，故选A.
5．已知抛物线y2＝8x的焦点为F，点P在该抛物线上，且P在y轴上的投影为点E，则|PF|－|PE|的值为( )
A．1 B．2
C．3 D．4
解析：选B 因为抛物线y2＝8x，所以抛物线的准线方程为x＝－2，因为P在y轴上的投影为点E，所以|PE|即为点P到x＝－2的距离减去2，因为点P在该抛物线上，
故点P到x＝－2的距离等于|PF|，
所以|PE|＝|PF|－2，故|PF|－|PE|＝2，故选B.
6．已知直线l过点(1,0)且垂直于x轴，若l被抛物线y2＝4ax截得的线段长为4，则抛物线的焦点坐标为________．
解析：由题知直线l的方程为x＝1，则直线与抛物线的交点为(1，±2eq \r(a))(a>0)．
又直线被抛物线截得的线段长为4，
所以4eq \r(a)＝4，即a＝1.所以抛物线的焦点坐标为(1,0)．
答案：(1,0)
二、综合练——练思维敏锐度
1．若抛物线y2＝2px上一点P(2，y0)到其准线的距离为4，则抛物线的标准方程为( )
A．y2＝4x B．y2＝6x
C．y2＝8x D．y2＝10x
解析：选C ∵抛物线y2＝2px，∴准线为x＝－eq \f(p,2).
∵点P(2，y0)到其准线的距离为4，∴eq \b\lc\|\rc\|(\a\vs4\al\c1(－\f(p,2)－2))＝4.
∴p＝4，∴抛物线的标准方程为y2＝8x.
2．已知抛物线C：y2＝x的焦点为F，A(x0，y0)是C上一点，|AF|＝eq \f(5,4)x0，则x0＝( )
A．1 B．2
C．4 D．8
解析：选A 由题意知抛物线的准线为x＝－eq \f(1,4).因为|AF|＝eq \f(5,4)x0，根据抛物线的定义可得x0＋eq \f(1,4)＝|AF|＝eq \f(5,4)x0，解得x0＝1.故选A.
3．双曲线eq \f(x2,m)－eq \f(y2,n)＝1(mn≠0)的离心率为2，有一个焦点与抛物线y2＝4x的焦点重合，则mn的值为( )
A.eq \f(3,16) B．eq \f(3,8)
C.eq \f(16,3) D．eq \f(8,3)
解析：选A ∵抛物线y2＝4x的焦点为(1,0)，∴双曲线中c＝1，又e＝2，∴eq \f(1,\r(m))＝2，∴m＝eq \f(1,4)，∴n＝eq \f(3,4)，∴mn＝eq \f(3,16).
4．已知点A(0,2)，抛物线C1：y2＝ax(a＞0)的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N.若|FM|∶|MN|＝1∶eq \r(5)，则a的值为( )
A.eq \f(1,4) B．eq \f(1,2)
C．1 D．4
解析：选D 依题意，点F的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a,4)，0))，如图，设点M在准线上的射影为K，由抛物线的定义知|MF|＝|MK|，|KM|∶|MN|＝1∶eq \r(5)，则|KN|∶|KM|＝2∶1.∵kFN＝eq \f(0－2,\f(a,4)－0)＝－eq \f(8,a)，kFN＝－eq \f(|KN|,|KM|)＝－2，∴eq \f(8,a)＝2，解得a＝4.
5．(2020·北京高考)设抛物线的顶点为O，焦点为F，准线为l，P是抛物线上异于O的一点，过P作PQ⊥l于Q.则线段FQ的垂直平分线( )
A．经过点O B．经过点P
C．平行于直线OP D．垂直于直线OP
解析：选B 连接PF，由题意及抛物线的定义可知|PQ|＝|FP|，则△QPF为等腰三角形，故线段FQ的垂直平分线经过点P.故选B.
6．已知抛物线y2＝4x的焦点为F，过焦点F的直线交抛物线于A，B两点，O为坐标原点．若△AOB的面积为4，则|AB|＝( )
A．6 B．8
C．12 D．16
解析：选D 设Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(y\\al(2,1),4)，y1))，Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(y\\al(2,2),4)，y2))，F(1,0)．当AB⊥x轴时，|AB|＝4，S△AOB＝eq \f(1,2)|OF|·|AB|＝2，不成立，所以eq \f(y2,\f(y\\al(2,2),4)－1)＝eq \f(y1,\f(y\\al(2,1),4)－1)⇒y1y2＝－4.由△AOB的面积为4，得eq \f(1,2)|y1－y2|×1＝4，所以yeq \\al(2,1)＋yeq \\al(2,2)＝56，因此|AB|＝x1＋x2＋p＝eq \f(y\\al(2,1)＋y\\al(2,2),4)＋2＝16.
7．(2021年1月新高考八省联考卷)已知抛物线y2＝2px上三点A(2,2)，B，C，直线AB，AC是圆(x－2)2＋y2＝1的两条切线，则直线BC的方程为( )
A．x＋2y＋1＝0 B．3x＋6y＋4＝0
C．2x＋6y＋3＝0 D．x＋3y＋2＝0
解析：选B 把A(2,2)代入y2＝2px得p＝1，
又直线AB，AC是圆(x－2)2＋y2＝1的两条切线，
易得AB方程为y－2＝eq \r(3)(x－2)，
AC方程为y－2＝－eq \r(3)(x－2)，
联立AB方程和抛物线方程得Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(8,3)－\f(4,\r(3))，\f(2,\r(3))－2))，
同理：Ceq \b\lc\(\rc\)(\a\vs4\al\c1(\f(8,3)＋\f(4,\r(3))，－\f(2,\r(3))－2))，
由B，C两点坐标可得直线BC的方程为3x＋6y＋4＝0，所以选B.
8．(多选)设抛物线C：y2＝2px(p>0)的焦点为F，准线为l，A为C上一点，以F为圆心，|FA|为半径的圆交l于B，D两点．若∠ABD＝90°，且△ABF的面积为9eq \r(3)，则下列说法正确的是( )
A．△ABF是等边三角形
B．|BF|＝3
C．点F到准线的距离为3
D．抛物线C的方程为y2＝6x
解析：选ACD ∵以F为圆心，|FA|为半径的圆交l于B，D两点，∠ABD＝90°，由抛物线的定义可得|AB|＝|AF|＝|BF|，∴△ABF是等边三角形，∴∠FBD＝30°.
∵△ABF的面积为eq \f(\r(3),4)|BF|2＝9eq \r(3)，∴|BF|＝6.又点F到准线的距离为|BF|sin 30°＝3＝p，则该抛物线的方程为y2＝6x.
9．(2021·海口调研)若抛物线y2＝8x上一点P(m，n)到其焦点的距离为8m，则m＝______.
解析：由题意得，抛物线的准线方程为x＝－2，
又点P(m，n) 到焦点的距离为8m，
所以|PF|＝m＋2＝8m，解得m＝eq \f(2,7).
答案：eq \f(2,7)
10．抛物线C：y2＝2px(p>0)的焦点为A，其准线与x轴的交点为B，如果在直线3x＋4y＋25＝0上存在点M，使得∠AMB＝90°，则实数p的取值范围是________．
解析：由题得Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))，Beq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(p,2)，0))，
∵M在直线3x＋4y＋25＝0上，设点Meq \b\lc\(\rc\)(\a\vs4\al\c1(x，\f(－3x－25,4)))，
∴ eq \(AM,\s\up7(―→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(p,2)，\f(－3x－25,4)))，eq \(BM,\s\up7(―→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(p,2)，\f(－3x－25,4))).
又∠AMB＝90°，
∴eq \(AM,\s\up7(―→))·eq \(BM,\s\up7(―→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(p,2)))·eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(p,2)))＋eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(－3x－25,4)))2＝0，
即25x2＋150x＋625－4p2＝0，∴Δ≥0，
即1502－4×25×(625－4p2)≥0，
解得p≥10，或p≤－10，
又p>0，∴p的取值范围是[10，＋∞)．
答案：[10，＋∞)
11．已知过抛物线y2＝2px(p>0)的焦点，斜率为2eq \r(2)的直线交抛物线于A(x1，y1)，B(x2，y2)(x10)的焦点，过点F的动直线l与抛物线C交于M，N两点，且当直线l的倾斜角为45°时，|MN|＝16.
(1)求抛物线C的方程；
(2)试确定在x轴上是否存在点P，使得直线PM，PN关于x轴对称？若存在，求出点P的坐标；若不存在，请说明理由．
解：(1)当直线l的倾斜角为45°时，l的斜率为1，
∵Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))，∴l的方程为y＝x－eq \f(p,2).
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝x－\f(p,2)，,y2＝2px，))得x2－3px＋eq \f(p2,4)＝0.
设M(x1，y1)，N(x2，y2)，则x1＋x2＝3p，
∴|MN|＝x1＋x2＋p＝4p＝16，p＝4，
∴抛物线C的方程为y2＝8x.
(2)假设满足题意的点P存在．
设P(a,0)，由(1)知F(2,0)，
①当直线l不与x轴垂直时，设l的方程为y＝k(x－2)(k≠0)，
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝kx－2，,y2＝8x))得k2x2－(4k2＋8)x＋4k2＝0，
则x1＋x2＝eq \f(4k2＋8,k2)，x1x2＝4.
Δ＝[－(4k2＋8)]2－4·k2·4k2＝64k2＋64>0，
∵直线PM，PN关于x轴对称，
∴kPM＋kPN＝0，
又kPM＝eq \f(kx1－2,x1－a)，kPN＝eq \f(kx2－2,x2－a)，
∴k(x1－2)(x2－a)＋k(x2－2)(x1－a)＝k[2x1x2－(a＋2)(x1＋x2)＋4a]＝－eq \f(8a＋2,k)＝0，
∴a＝－2，此时P(－2,0)．
②当直线l与x轴垂直时，由抛物线的对称性，易知PM，PN关于x轴对称，此时只需P与焦点F不重合即可．
综上，存在唯一的点P(－2,0)，使直线PM，PN关于x轴对称．
三、自选练——练高考区分度
1．抛物线有如下光学性质：过焦点的光线经抛物线反射后得到的光线平行于抛物线的对称轴；反之，平行于抛物线对称轴的光线经抛物线反射后必过抛物线的焦点．已知抛物线y2＝4x的焦点为F，一条平行于x轴的光线从点M(3,1)射出，经过抛物线上的点A反射后，再经过抛物线上的另一点B射出，则△ABM的周长为( )
A.eq \f(71,12)＋eq \r(26) B．9＋eq \r(10)
C.eq \f(83,12)＋eq \r(26) D．9＋eq \r(26)
解析：选D 对于y2＝4x，令y＝1，得x＝eq \f(1,4)，即Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,4)，1))，结合抛物线的光学性质，得AB经过焦点F，设直线AB的方程为y＝k(x－1)，与抛物线方程联立可得，k2x2－2(k2＋2)x＋k2＝0，据此可得xAxB＝1，∴xB＝eq \f(1,xA)＝4.
∴|AB|＝xA＋xB＋p＝eq \f(25,4).
将x＝4代入y2＝4x可得y＝±4，故B(4，－4)，
∴|MB|＝eq \r(4－32＋－4－12)＝eq \r(26).
∴△ABM的周长为|MA|＋|MB|＋|AB|＝eq \b\lc\(\rc\)(\a\vs4\al\c1(3－\f(1,4)))＋eq \f(25,4)＋eq \r(26)＝9＋eq \r(26).故选D.
2．(多选)设F是抛物线C：y2＝4x的焦点，直线l过点F，且与抛物线C交于A，B两点，O为坐标原点，则下列结论正确的是( )
A．|AB|≥4
B．|OA|＋|OB|>8
C．若点P(2,2)，则|PA|＋|AF|的最小值是3
D．△OAB的面积的最小值是2
解析：选ACD F(1,0)，如图，不妨设A在第一象限．
(1)若直线l斜率不存在，则A(1,2)，B(1，－2)，则|AB|＝4，|OA|＋|OB|＝2|OA|＝2eq \r(5)，S△OAB＝eq \f(1,2)×4×1＝2，显然B错误；
(2)若直线l斜率存在，设直线l斜率为k，则直线l的方程为y＝k(x－1)，显然k≠0，
联立方程组eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝kx－1，,y2＝4x，))消元得：k2x2－(2k2＋4)x＋k2＝0，设A(x1，y1)，B(x2，y2)，则x1＋x2＝eq \f(2k2＋4,k2)＝2＋eq \f(4,k2)，∴|AB|＝x1＋x2＋2＝4＋eq \f(4,k2)>4，原点O到直线l的距离d＝eq \f(|k|,\r(k2＋1))，∴S△OAB＝eq \f(1,2)×|AB|×d＝eq \f(1,2)×eq \b\lc\(\rc\)(\a\vs4\al\c1(4＋\f(4,k2)))×eq \f(|k|,\r(k2＋1))＝2eq \r(1＋\f(1,k2))>2.
综上，|AB|≥4，S△OAB≥2，故A正确，D正确．过点A向准线作垂线，垂足为N，则|PA|＋|AF|＝|PA|＋|AN|，又P(2,2)在抛物线右侧，故当P，A，N三点共线时，|PA|＋|AF|取得最小值3，故C正确．故选A、C、D.
3．(多选)已知过抛物线C：y2＝4x焦点的直线交抛物线C于P，Q两点，交圆x2＋y2－2x＝0于M，N两点，其中P, M位于第一象限，则eq \f(1,|PM|)＋eq \f(4,|QN|)的值可能为( )
A．3 B．4
C．5 D．6
解析：选BCD 如图所示，可设eq \b\lc\|\rc\|(\a\vs4\al\c1(PF))＝m，eq \b\lc\|\rc\|(\a\vs4\al\c1(QF))＝n，则eq \b\lc\|\rc\|(\a\vs4\al\c1(PM))＝m－1，eq \b\lc\|\rc\|(\a\vs4\al\c1(QN))＝n－1，∵y2＝4x，∴p＝2，根据抛物线的常用结论，有eq \f(1,m)＋eq \f(1,n)＝eq \f(2,p)＝1，∴eq \f(m＋n,mn)＝1，则m＋n＝mn，
∴eq \f(1,|PM|)＋eq \f(4,|QN|)＝eq \f(1,m－1)＋eq \f(4,n－1)＝eq \f(4m＋n－5,mn－m＋n＋1)＝4m＋n－5，
又∵(4m＋n)·1＝(4m＋n)·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,m)＋\f(1,n)))＝4＋eq \f(4m,n)＋eq \f(n,m)＋1≥5＋2 eq \r(\f(4m,n)·\f(n,m))＝9，得4m＋n≥9，
∴4m＋n－5≥4，则eq \f(1,|PM|)＋eq \f(4,|QN|)的值不可能为3.标准方程
y2＝2px
(p＞0)
y2＝－2px(p＞0)
x2＝2py(p>0)
x2＝－2py
(p>0)
p的几何意义：焦点F到准线l的距离
图形
顶点
O(0,0)
对称轴
x轴
y轴
焦点
Feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(p,2)，0))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(p,2)))
Feq \b\lc\(\rc\)(\a\vs4\al\c1(0，－\f(p,2)))
离心率
e＝1
准线方程
x＝－eq \f(p,2)
x＝eq \f(p,2)
y＝－eq \f(p,2)
y＝eq \f(p,2)
范围
x≥0，y∈R
x≤0，y∈R
y≥0，x∈R
y≤0，x∈R
开口方向
向右
向左
向上
向下
焦半径(其中
P(x0，y0))
|PF|＝x0＋eq \f(p,2)
|PF|＝－x0＋eq \f(p,2)
|PF|＝y0＋eq \f(p,2)
|PF|＝－y0＋eq \f(p,2)
轨迹
问题
用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是否为抛物线
距离
问题
涉及抛物线上的点到焦点的距离和点到准线的距离问题时，注意在解题中利用两者之间的相互转化