新高考数学一轮复习教案第8章第5节 双曲线（含解析）

这是一份新高考数学一轮复习教案第8章第5节 双曲线（含解析），共25页。
1.结合双曲线的定义，求轨迹方程及焦点三角形，凸显数学运算、直观想象的核心素养．
2．结合双曲线几何性质(范围、对称性、顶点、离心率、渐近线)，考查求相关量的计算，凸显逻辑推理、数学运算的核心素养．
[理清主干知识]
1．双曲线的定义
平面内与两个定点F1，F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．
集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c，其中a，c为常数且a>0，c>0.
(1)当2a|F1F2|时，P点不存在．
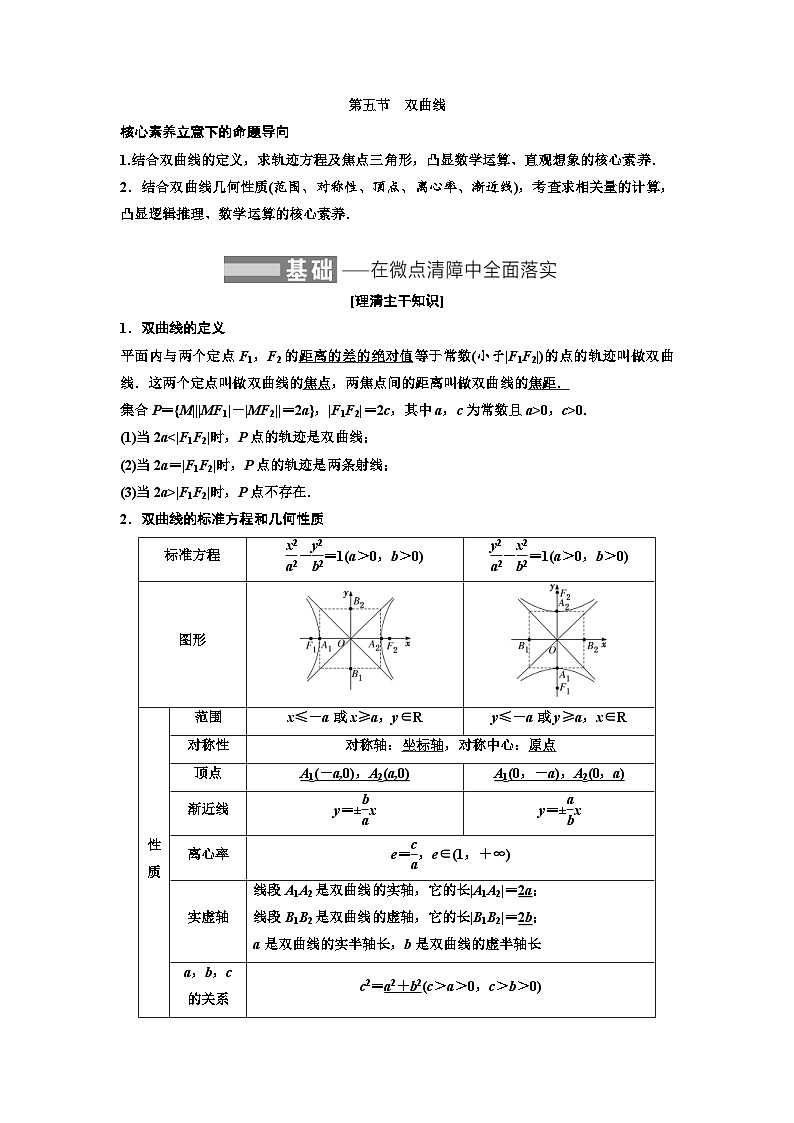
2．双曲线的标准方程和几何性质
3．常用结论
(1)双曲线的焦点到其渐近线的距离为b.
(2)若P是双曲线右支上一点，F1，F2分别为双曲线的左、右焦点，则|PF1|min＝a＋c，|PF2|min＝c－a.
(3)等轴双曲线
①定义：中心在原点，以坐标轴为对称轴，实半轴长与虚半轴长相等的双曲线叫做等轴双曲线．
②性质：a＝b；e＝eq \r(2)；渐近线互相垂直；等轴双曲线上任意一点到中心的距离是它到两焦点距离的等比中项．
(4)共轭双曲线
①定义：如果一条双曲线的实轴和虚轴分别是另一条双曲线的虚轴和实轴，那么这两条双曲线互为共轭双曲线．
②性质：它们有共同的渐近线；它们的四个焦点共圆；它们的离心率的倒数的平方和等于1.
[澄清盲点误点]
一、关键点练明
1．(双曲线的定义)设F1，F2分别是双曲线x2－eq \f(y2,9)＝1的左、右焦点．若点P在双曲线上，且|PF1|＝5，则|PF2|＝( )
A．5 B．3
C．7 D．3或7
解析：选D ∵||PF1|－|PF2||＝2，∴|PF2|＝7或3.
2．(双曲线的实轴)双曲线2x2－y2＝8的实轴长是( )
A．2 B．2eq \r(2)
C．4 D．4eq \r(2)
解析：选C 双曲线2x2－y2＝8的标准方程为eq \f(x2,4)－eq \f(y2,8)＝1，故实轴长为4.
3．(双曲线的渐近线)若双曲线C：eq \f(x2,m)－y2＝1(m>0)的一条渐近线方程为3x＋2y＝0，则实数m＝( )
A.eq \f(4,9) B．eq \f(9,4)
C.eq \f(2,3) D．eq \f(3,2)
答案：A
4．(双曲线的标准方程)以椭圆eq \f(x2,4)＋eq \f(y2,3)＝1的焦点为顶点，顶点为焦点的双曲线方程为__________．
解析：设所求的双曲线方程为eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)，
由椭圆eq \f(x2,4)＋eq \f(y2,3)＝1，得焦点为(±1,0)，顶点为(±2,0)．
所以双曲线的顶点为(±1,0)，焦点为(±2,0)．
所以a＝1，c＝2，所以b2＝c2－a2＝3，
所以双曲线标准方程为x2－eq \f(y2,3)＝1.
答案：x2－eq \f(y2,3)＝1
5．(双曲线的离心率)若双曲线eq \f(x2,a2)－eq \f(y2,4)＝1(a＞0)的离心率为eq \f(\r(5),2)，则a＝________.
解析：设焦距为2c，则eq \f(c,a)＝eq \f(\r(5),2)，即c2＝eq \f(5,4)a2.由c2＝a2＋4得eq \f(5,4)a2＝a2＋4，所以a2＝16，所以a＝4.
答案：4
二、易错点练清
1．(忽视双曲线定义的条件)平面内到点F1(0,4)，F2(0，－4)的距离之差等于6的点的轨迹是________________．
解析：由|PF1|－|PF2|＝62，故|PF2|＝6.
答案：6
3．(忽视焦点的位置)以坐标原点为对称中心，两坐标轴为对称轴的双曲线的一条渐近线的倾斜角为eq \f(π,3)，则双曲线的离心率为________．
解析：若双曲线的焦点在x轴上，
设双曲线的方程为eq \f(x2,a2)－eq \f(y2,b2)＝1，
则渐近线的方程为y＝±eq \f(b,a)x，
由题意可得eq \f(b,a)＝taneq \f(π,3)＝eq \r(3)，b＝eq \r(3)a，可得c＝2a，
则e＝eq \f(c,a)＝2；若双曲线的焦点在y轴上，
设双曲线的方程为eq \f(y2,a2)－eq \f(x2,b2)＝1，
则渐近线的方程为y＝±eq \f(a,b)x，
由题意可得eq \f(a,b)＝taneq \f(π,3)＝eq \r(3)，a＝eq \r(3)b，
可得c＝eq \f(2\r(3),3)a，则e＝eq \f(2\r(3),3).综上可得e＝2或e＝eq \f(2\r(3),3).
答案：2或eq \f(2\r(3),3)
考点一 双曲线的定义及其应用
考法(一) 利用定义求轨迹方程
[例1] 已知圆C1：(x＋3)2＋y2＝1和圆C2：(x－3)2＋y2＝9，动圆M同时与圆C1及圆C2外切，则动圆圆心M的轨迹方程为____________________．
[解析] 如图所示，设动圆M与圆C1及圆C2分别外切于点A和点B，根据两圆外切的充要条件，得
|MC1|－|AC1|＝|MA|，
|MC2|－|BC2|＝|MB|.
因为|MA|＝|MB|，
所以|MC2|－|MC1|＝|BC2|－|AC1|＝3－1＝20)的左焦点为(－3,0)，且C的离心率为eq \f(3,2)，则C的方程为( )
A.eq \f(y2,4)－eq \f(x2,5)＝1 B．eq \f(y2,5)－eq \f(x2,4)＝1
C.eq \f(x2,4)－eq \f(y2,5)＝1 D．eq \f(x2,5)－eq \f(y2,4)＝1
解析：选C 由题意，可得c＝3，又由e＝eq \f(c,a)＝eq \f(3,2)，∴a＝2，
又b2＝32－22＝5，故C的方程为eq \f(x2,4)－eq \f(y2,5)＝1，故选C.
2．(2020·天津高考)设双曲线C的方程为eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)，过抛物线y2＝4x的焦点和点(0，b)的直线为l.若C的一条渐近线与l平行，另一条渐近线与l垂直，则双曲线C的方程为( )
A.eq \f(x2,4)－eq \f(y2,4)＝1 B．x2－eq \f(y2,4)＝1
C.eq \f(x2,4)－y2＝1 D．x2－y2＝1
解析：选D 法一：由题知y2＝4x的焦点坐标为(1,0)，则过焦点和点(0，b)的直线方程为x＋eq \f(y,b)＝1，而eq \f(x2,a2)－eq \f(y2,b2)＝1的渐近线方程为eq \f(x,a)＋eq \f(y,b)＝0和eq \f(x,a)－eq \f(y,b)＝0，由l与一条渐近线平行，与另一条渐近线垂直，得a＝1，b＝1，故选D.
法二：由题知双曲线C的两条渐近线互相垂直，则a＝b，即渐近线方程为x±y＝0，排除B、C.又知y2＝4x的焦点坐标为(1,0)，l过点(1,0)，(0，b)，所以eq \f(b－0,0－1)＝－1，b＝1，故选D.
考点三 双曲线的几何性质
考法(一) 求双曲线的渐近线方程
[例1] (1)(2021·湖南长沙模拟)已知双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的左、右焦点分别为F1，F2，M为双曲线上一点，若cs∠F1MF2＝eq \f(1,4)，|MF1|＝2|MF2|，则此双曲线的渐近线方程为( )
A．y＝±eq \r(3)x B．y＝±eq \f(\r(3),3)x
C．y＝±x D．y＝±2x
(2)已知双曲线C：eq \f(x2,3)－y2＝1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为M，N.若△OMN为直角三角形，则|MN|＝( )
A.eq \f(3,2) B．3
C．2eq \r(3) D．4
[解析] (1)由题意，得|MF1|－|MF2|＝2a，
又|MF1|＝2|MF2|，∴|MF1|＝4a，|MF2|＝2a，
∴cs∠F1MF2＝eq \f(16a2＋4a2－4c2,2×4a×2a)＝eq \f(1,4)，
化简得c2＝4a2，即a2＋b2＝4a2，∴b2＝3a2，
又a>0，b>0，∴eq \f(b,a)＝eq \r(3)，
∴此双曲线的渐近线方程为y＝±eq \r(3)x，故选A.
(2)法一：由已知得双曲线的两条渐近线方程为y＝±eq \f(1,\r(3))x.设两条渐近线的夹角为2α，则有tan α＝eq \f(1,\r(3))＝eq \f(\r(3),3)，所以α＝30°.所以∠MON＝2α＝60°.又△OMN为直角三角形，由于双曲线具有对称性，不妨设MN⊥ON，如图所示．在Rt△ONF中，|OF|＝2，则|ON|＝eq \r(3).在Rt△OMN中，|MN|＝|ON|·tan 2α＝eq \r(3)·tan 60°＝3.故选B.
法二：因为双曲线eq \f(x2,3)－y2＝1的渐近线方程为y＝±eq \f(\r(3),3)x，所以∠MON＝60°.不妨设过点F的直线与直线y＝eq \f(\r(3),3)x交于点M，由△OMN为直角三角形，不妨设∠OMN＝90°，则 ∠MFO＝60°，又直线MN过点F(2,0)，所以直线MN的方程为y＝－eq \r(3)(x－2)，
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y＝－\r(3)x－2，,y＝\f(\r(3),3)x，))得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝\f(3,2)，,y＝\f(\r(3),2)，))
所以Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)，\f(\r(3),2)))，所以|OM|＝ eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))2＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)))2)＝eq \r(3)，
所以|MN|＝eq \r(3)|OM|＝3，故选B.
[答案] (1)A (2)B
[方法技巧]
涉及双曲线渐近线的几个常用结论
(1)求双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)或eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)的渐近线方程的方法是令右边的常数等于0，即令eq \f(x2,a2)－eq \f(y2,b2)＝0，得y＝±eq \f(b,a)x，或令eq \f(y2,a2)－eq \f(x2,b2)＝0，得y＝±eq \f(a,b)x.
(2)已知渐近线方程为y＝±eq \f(b,a)x，可设双曲线方程为eq \f(x2,a2)－eq \f(y2,b2)＝λ(a>0，b>0，λ≠0)．
[提醒] 两条渐近线的倾斜角互补，斜率互为相反数，且两条渐近线关于x轴、y轴对称．
考法(二) 求双曲线的离心率
[例2] (1)若双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1 (a>0，b>0)的渐近线与圆(x－3)2＋y2＝1无交点，则C的离心率的取值范围为( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(3\r(2),4))) B．eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(2\r(3),3)))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3\r(2),4)，＋∞)) D．eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(3),3)，＋∞))
(2)(2019·全国卷Ⅰ)已知双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的左、右焦点分别为F1，F2，过F1的直线与C的两条渐近线分别交于A，B两点．若eq \(F1A,\s\up7(―→))＝eq \(AB,\s\up7(―→))，eq \(F1B,\s\up7(―→))·eq \(F2B,\s\up7(―→))＝0，则C的离心率为________．
[解析] (1)∵双曲线渐近线为bx±ay＝0与圆(x－3)2＋y2＝1无交点，
∴圆心到渐近线的距离大于半径，即eq \f(3b,\r(a2＋b2))＞1，
∴8b2＞a2，∴8(c2－a2)＞a2，即8c2>9a2，
∴e＝eq \f(c,a)＞eq \f(3\r(2),4).故选C.
(2)法一：由eq \(F1A,\s\up7(―→))＝eq \(AB,\s\up7(―→))，得A为F1B的中点．
又∵O为F1F2的中点，
∴OA∥BF2.
又eq \(F1B,\s\up7(―→))·eq \(F2B,\s\up7(―→))＝0，∴∠F1BF2＝90°.
∴|OF2|＝|OB|，
∴∠OBF2＝∠OF2B.
又∵∠F1OA＝∠BOF2，∠F1OA＝∠OF2B，
∴∠BOF2＝∠OF2B＝∠OBF2，
∴△OBF2为等边三角形．
如图所示，不妨设B为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(c,2)，－\f(\r(3),2)c)).
∵点B在直线y＝－eq \f(b,a)x上，∴eq \f(b,a)＝eq \r(3)，
∴离心率e＝eq \f(c,a)＝eq \r(1＋\f(b2,a2))＝2.
法二：∵eq \(F1B,\s\up7(―→))·eq \(F2B,\s\up7(―→))＝0，∴∠F1BF2＝90°.在Rt△F1BF2中，O为F1F2的中点，∴|OF2|＝|OB|＝c.如图，作BH⊥x轴于H，由l1为双曲线的渐近线，可得eq \f(|BH|,|OH|)＝eq \f(b,a)，且|BH|2＋|OH|2＝|OB|2＝c2，∴|BH|＝b，|OH|＝a，∴B(a，－b)，F2(c,0)．
又∵eq \(F1A,\s\up7(―→))＝eq \(AB,\s\up7(―→))，∴A为F1B的中点．
∴OA∥F2B，∴eq \f(b,a)＝eq \f(b,c－a)，∴c＝2a，∴离心率e＝eq \f(c,a)＝2.
[答案] (1)C (2)2
[方法技巧]
1．求双曲线的离心率或其范围的方法
(1)求a，b，c的值，由eq \f(c2,a2)＝eq \f(a2＋b2,a2)＝1＋eq \f(b2,a2)直接求e.
(2)列出含有a，b，c的齐次方程(或不等式)，借助b2＝c2－a2消去b，然后转化成关于e的方程(或不等式)求解，注意e的取值范围．
(3)因为离心率是比值，所以可以利用特殊值法．例如，令a＝1，求出相应c的值，进而求出离心率，能有效简化计算．
(4)通过特殊位置求出离心率．
2．双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的渐近线的斜率k与离心率e的关系：当k>0时，k＝eq \f(b,a)＝eq \f(\r(c2－a2),a)＝ eq \r(\f(c2,a2)－1)＝eq \r(e2－1)；当k0)．由题意可知a＝8，图中的A点坐标为(10,10)．将a＝8，(10,10)代入双曲线方程，可得b＝eq \f(40,3)，所以eq \f(b,a)＝eq \f(5,3)，所以e＝eq \r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(b,a)))2)＝eq \f(\r(34),3).
答案：eq \f(\r(34),3)
eq \a\vs4\al([课时跟踪检测])
一、基础练——练手感熟练度
1．双曲线eq \f(x2,2)－y2＝1的实轴长为( )
A．4 B．2
C．2eq \r(3) D．2eq \r(2)
解析：选D 由题知a2＝2，∴a＝eq \r(2)，故实轴长为2a＝2eq \r(2)，故选D.
2．双曲线eq \f(x2,5)－eq \f(y2,10)＝1的渐近线方程为( )
A．y＝±eq \f(1,2)x B．y＝±eq \f(\r(2),2)x
C．y＝±eq \r(2)x D．y＝±2x
解析：选C 双曲线eq \f(x2,5)－eq \f(y2,10)＝1的渐近线方程为eq \f(x2,5)－eq \f(y2,10)＝0，整理得y2＝2x2，
解得y＝±eq \r(2)x，故选C.
3．已知双曲线eq \f(x2,4)－eq \f(y2,b2)＝1(b>0)的渐近线方程为eq \r(3)x±y＝0，则b＝( )
A．2eq \r(3) B．eq \r(3)
C.eq \f(\r(3),2) D．12
解析：选A 因为双曲线eq \f(x2,4)－eq \f(y2,b2)＝1(b>0)的渐近线方程为y＝±eq \f(b,2)x，又渐近线方程为y＝±eq \r(3)x，所以eq \f(b,2)＝eq \r(3)，b＝2eq \r(3)，故选A.
4．设双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的虚轴长为4，一条渐近线为y＝eq \f(1,2)x，则双曲线C的方程为( )
A.eq \f(x2,16)－eq \f(y2,4)＝1 B．eq \f(x2,4)－eq \f(y2,16)＝1
C.eq \f(x2,64)－eq \f(y2,16)＝1 D．x2－eq \f(y2,4)＝1
解析：选A 因为双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的虚轴长为4，所以2b＝4，b＝2，
因为双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的一条渐近线为y＝eq \f(1,2)x，所以eq \f(b,a)＝eq \f(1,2)⇒a＝2b＝4，
所以双曲线M的方程为eq \f(x2,16)－eq \f(y2,4)＝1，故选A.
5．若a＞1，则双曲线eq \f(x2,a2)－y2＝1的离心率的取值范围是( )
A．(eq \r(2)，＋∞) B．(eq \r(2)，2)
C．(1，eq \r(2)) D．(1,2)
解析：选C 由题意得双曲线的离心率e＝eq \f(\r(a2＋1),a)，
即e2＝eq \f(a2＋1,a2)＝1＋eq \f(1,a2).
∵a＞1，∴0＜eq \f(1,a2)＜1，∴1＜1＋eq \f(1,a2)＜2，∴1＜e＜eq \r(2).
6．(2020·北京高考)已知双曲线C：eq \f(x2,6)－eq \f(y2,3)＝1，则C的右焦点的坐标为________；C的焦点到其渐近线的距离是________．
解析：双曲线C：eq \f(x2,6)－eq \f(y2,3)＝1中，c2＝6＋3＝9，∴c＝3，则C的右焦点的坐标为(3,0)．C的渐近线方程为y＝±eq \f(\r(3),\r(6))x，即y＝±eq \f(1,\r(2))x，即x±eq \r(2)y＝0，则C的焦点到其渐近线的距离d＝eq \f(3,\r(3))＝eq \r(3).
答案：(3,0) eq \r(3)
二、综合练——练思维敏锐度
1．若实数k满足0＜k＜9，则曲线eq \f(x2,25)－eq \f(y2,9－k)＝1与曲线eq \f(x2,25－k)－eq \f(y2,9)＝1的( )
A．离心率相等 B．虚半轴长相等
C．实半轴长相等 D．焦距相等
解析：选D 由00)的右焦点是F，左、右顶点分别是A1，A2，过F作A1A2的垂线与双曲线交于B, C两点．若A1B⊥A2C，则该双曲线的渐近线的斜率为( )
A．±eq \f(1,2) B．±eq \f(\r(2),2)
C．±1 D．±eq \r(2)
解析：选C 由题设易知A1(－a,0)，A2(a,0)，Beq \b\lc\(\rc\)(\a\vs4\al\c1(c，\f(b2,a)))，Ceq \b\lc\(\rc\)(\a\vs4\al\c1(c，－\f(b2,a))).∵A1B⊥A2C，∴eq \f(\f(b2,a),c＋a)·eq \f(－\f(b2,a),c－a)＝－1，整理得a＝b.∵渐近线方程为y＝±eq \f(b,a)x，即y＝±x，∴渐近线的斜率为±1.
3．已知双曲线eq \f(x2,4)－eq \f(y2,2)＝1的右焦点为F，P为双曲线左支上一点，点A(0，eq \r(2))，则 △APF周长的最小值为( )
A．4(1＋eq \r(2)) B．4＋eq \r(2)
C．2(eq \r(2)＋eq \r(6)) D．eq \r(6)＋3eq \r(2)
解析：选A 设双曲线的左焦点为F′，易得点F(eq \r(6)，0)，△APF的周长l＝|AF|＋|AP|＋|PF|＝|AF|＋2a＋|PF′|＋|AP|，要使△APF的周长最小，只需|AP|＋|PF′|最小，易知当A，P，F′三点共线时取到最小值，故l＝2|AF|＋2a＝4(1＋eq \r(2))．故选A.
4．在平面直角坐标系xOy中，已知双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)的离心率为eq \r(5)，从双曲线C的右焦点F引渐近线的垂线，垂足为A，若△AFO的面积为1，则双曲线C的方程为( )
A.eq \f(x2,2)－eq \f(y2,8)＝1 B．eq \f(x2,4)－y2＝1
C.eq \f(x2,4)－eq \f(y2,16)＝1 D．x2－eq \f(y2,4)＝1
解析：选D 因为双曲线C的右焦点F到渐近线的距离|FA|＝b，|OA|＝a，所以ab＝2，又双曲线C的离心率为eq \r(5)，所以 eq \r(1＋\f(b2,a2))＝eq \r(5)，即b2＝4a2，解得a2＝1，b2＝4，所以双曲线C的方程为x2－eq \f(y2,4)＝1，故选D.
5．(2020·全国卷Ⅱ)设O为坐标原点，直线x＝a与双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)的两条渐近线分别交于D，E两点．若△ODE的面积为8，则C的焦距的最小值为( )
A．4 B．8
C．16 D．32
解析：选B 由题意知双曲线的渐近线方程为y＝±eq \f(b,a)x.因为D，E分别为直线x＝a与双曲线C的两条渐近线的交点，所以不妨设D(a，b)，E(a，－b)，所以S△ODE＝eq \f(1,2)×a×|DE|＝eq \f(1,2)×a×2b＝ab＝8，所以c2＝a2＋b2≥2ab＝16，所以c≥4，所以2c≥8，所以C的焦距的最小值为8，故选B.
6．已知双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1的一条渐近线l的倾斜角为eq \f(π,3)，且C的一个焦点到l的距离为eq \r(3)，则双曲线C的方程为( )
A.eq \f(x2,12)－eq \f(y2,4)＝1 B．eq \f(x2,4)－eq \f(y2,12)＝1
C.eq \f(x2,3)－y2＝1 D．x2－eq \f(y2,3)＝1
解析：选D 由eq \f(x2,a2)－eq \f(y2,b2)＝0可得y＝±eq \f(b,a)x，即渐近线的方程为y＝±eq \f(b,a)x，又一条渐近线l的倾斜角为eq \f(π,3)，
所以eq \f(b,a)＝taneq \f(π,3)＝eq \r(3).
因为双曲线C的一个焦点(c,0)到l的距离为eq \r(3)，
所以eq \f(|bc|,\r(a2＋b2))＝b＝eq \r(3)，
所以a＝1，
所以双曲线的方程为x2－eq \f(y2,3)＝1.
7．(2021·黄山一诊)双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的一条渐近线与直线x＋2y＋1＝0垂直，F1，F2为C的焦点，A为双曲线上一点，若|F1A|＝2|F2A|，则cs∠AF2F1等于( )
A.eq \f(\r(3),2) B．eq \f(\r(5),4)
C.eq \f(\r(5),5) D．eq \f(1,4)
解析：选C 因为双曲线的一条渐近线与直线x＋2y＋1＝0垂直，所以b＝2a.又|F1A|＝2|F2A|，且|F1A|－|F2A|＝2a，所以|F2A|＝2a，|F1A|＝4a，而c2＝5a2，得2c＝2eq \r(5)a，所以cs∠AF2F1＝eq \f(|F1F2|2＋|F2A|2－|F1A|2,2|F1F2||F2A|)＝eq \f(20a2＋4a2－16a2,2×2\r(5)a×2a)＝eq \f(\r(5),5)，故选C.
8．(多选)设F1，F2是双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的左、右焦点，O是坐标原点．过F2作C的一条渐近线的垂线，垂足为P.若|PF1|＝eq \r(6)|OP|，则下列说法正确的是( )
A．|F2P|＝b
B．双曲线的离心率为eq \r(3)
C．双曲线的渐近线方程为y＝±eq \r(3)x
D．点P在直线x＝eq \f(\r(3),3)a上
解析：选ABD 由双曲线的性质可知，双曲线的一条渐近线方程为y＝eq \f(b,a)x，即bx－ay＝0，
设焦点F1(－c,0)，F2(c,0)(a>0，b>0，c>0)，
因为过F2作C的一条渐近线的垂线，垂足为P，
所以|F2P|＝eq \f(|bc－a×0|,\r(a2＋b2))＝eq \f(bc,c)＝b，故A正确；
因为|OP|＝eq \r(|OF2|2－|PF2|2)＝eq \r(c2－b2)＝a，所以|PF1|＝eq \r(6)|OP|＝eq \r(6)a，cs∠F1OP＝cs(180°－∠F2OP)＝－cs∠F2OP＝－eq \f(|OP|,|OF2|)＝－eq \f(a,c)，
在三角形OPF1中，根据余弦定理可知cs∠F1OP＝eq \f(|OP|2＋|OF1|2－|F1P|2,2|OP|·|OF1|)＝eq \f(a2＋c2－6a2,2ac)＝－eq \f(a,c)，解得3a2＝c2，即离心率e＝eq \r(3)或e＝－eq \r(3)(舍去)，故B正确；
因为e＝ eq \r(1＋\f(b2,a2))＝eq \r(3)，解得eq \f(b,a)＝eq \r(2)，所以渐近线的方程为y＝±eq \r(2)x，故C错误；
因为点P在直线y＝eq \r(2)x上，可设P(x，eq \r(2)x)(x>0)，由|OP|＝a可知，|OP|＝eq \r(x2＋\r(2)x2)＝eq \r(3)x＝a，解得x＝eq \f(\r(3),3)a，故D正确．
9．已知双曲线C：eq \f(x2,12)－eq \f(y2,4)＝1，O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点分别为P，Q，若△POQ为直角三角形，则|PQ|＝( )
A．2 B．4
C．6 D．8
解析：选C 对于双曲线C：eq \f(x2,12)－eq \f(y2,4)＝1，右焦点为F(4,0)，双曲线的两条渐近线方程为y＝±eq \f(\r(3),3)x，由过点F的直线交两渐近线于P，Q，不妨设点P在第一象限，点Q在第四象限，∠OPQ＝90°，如图所示，
则在Rt△POQ中，∠POQ＝60°.
又∠POF＝30°，|OF|＝4，∴|OP|＝2eq \r(3)，
∴|PQ|＝eq \r(3)|OP|＝6.故选C.
10．已知曲线eq \f(x2,2)＋eq \f(y2,k2－k)＝1，当曲线表示焦点在y轴上的椭圆时k的取值范围是________；当曲线表示双曲线时k的取值范围是________．
解析：当曲线表示焦点在y轴上的椭圆时，k2－k＞2，
所以k＜－1或k＞2；
当曲线表示双曲线时，k2－k＜0，所以0＜k＜1.
答案：(－∞，－1)∪(2，＋∞) (0,1)
11．若点P是以A(－3,0)，B(3,0)为焦点，实轴长为2eq \r(5)的双曲线与圆x2＋y2＝9的一个交点，则|PA|＋|PB|＝________.
解析：不妨设点P在双曲线的右支上，则|PA|＞|PB|.
因为点P是双曲线与圆的交点，
所以由双曲线的定义知，|PA|－|PB|＝2eq \r(5)，①
又|PA|2＋|PB|2＝36，②
联立①②化简得2|PA|·|PB|＝16，
所以(|PA|＋|PB|)2＝|PA|2＋|PB|2＋2|PA|·|PB|＝52，所以|PA|＋|PB|＝2eq \r(13).
答案：2eq \r(13)
12．已知双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)的两条渐近线与抛物线y2＝4x的准线分别交于A，B两点，O为坐标原点，若S△AOB＝2eq \r(3)，则双曲线的离心率e＝________.
解析：由题意，知抛物线的准线方程是x＝－1，双曲线的渐近线方程是y＝±eq \f(b,a)x.当x＝－1时，y＝±eq \f(b,a)，即Aeq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(b,a)))，Beq \b\lc\(\rc\)(\a\vs4\al\c1(－1，－\f(b,a)))或Aeq \b\lc\(\rc\)(\a\vs4\al\c1(－1，－\f(b,a)))，Beq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(b,a))).所以S△AOB＝eq \f(1,2)×2×eq \f(b,a)×1＝2eq \r(3)，即eq \f(b,a)＝2eq \r(3)，所以e＝ eq \r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(b,a)))2)＝eq \r(13).
答案：eq \r(13)
13．已知双曲线C：x2－eq \f(y2,8)＝1，过左焦点F1的直线l与双曲线C的左支以及渐近线y＝2eq \r(2)x交于A，B两点，若F1A―→＝AB―→，求直线l的斜率．
解：由题意知，双曲线C的左焦点F1(－3，0)，故设直线l的方程为y＝k(x＋3)，与y＝2eq \r(2)x联立，得Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3k,2\r(2)－k)，\f(6\r(2)k,2\r(2)－k)))，
由F1A―→＝AB―→，得A为F1B的中点，
由中点坐标公式得Aeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3k－\r(2),2\r(2)－k)，\f(3\r(2)k,2\r(2)－k))).
∵点A在双曲线上，∴eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3k－\r(2),2\r(2)－k)))2－eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(3\r(2)k,2\r(2)－k)))2,8)＝1.
即23k2－56eq \r(2)k＋40＝0，解得k＝eq \f(10\r(2),23)或k＝2eq \r(2)(舍去)．
14．已知双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的右焦点为F(c,0)．
(1)若双曲线的一条渐近线方程为y＝x且c＝2，求双曲线的方程；
(2)以原点O为圆心，c为半径作圆，该圆与双曲线在第一象限的交点为A，过A作圆的切线，斜率为－eq \r(3)，求双曲线的离心率．
解：(1)因为双曲线的渐近线方程为y＝±eq \f(b,a)x，所以a＝b，
所以c2＝a2＋b2＝2a2＝4，所以a2＝b2＝2，
所以双曲线的方程为eq \f(x2,2)－eq \f(y2,2)＝1.
(2)设点A的坐标为(x0，y0)，
所以直线AO的斜率满足eq \f(y0,x0)·(－eq \r(3))＝－1，
所以x0＝eq \r(3)y0，①
依题意，圆的方程为x2＋y2＝c2，
将①代入圆的方程得3yeq \\al(2,0)＋yeq \\al(2,0)＝c2，
即y0＝eq \f(1,2)c，
所以x0＝eq \f(\r(3),2)c，所以点A的坐标为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),2)c，\f(1,2)c))，
代入双曲线方程得eq \f(\f(3,4)c2,a2)－eq \f(\f(1,4)c2,b2)＝1，
即eq \f(3,4)b2c2－eq \f(1,4)a2c2＝a2b2，②
又因为a2＋b2＝c2，所以将b2＝c2－a2代入②式，
整理得eq \f(3,4)c4－2a2c2＋a4＝0，
所以3eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(c,a)))4－8eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(c,a)))2＋4＝0，所以(3e2－2)(e2－2)＝0，
因为e>1，所以e＝eq \r(2)，所以双曲线的离心率为eq \r(2).
三、自选练——练高考区分度
1．过双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)的右顶点A作斜率为－1的直线，该直线与双曲线的两条渐近线的交点分别为B，C.若eq \(AB,\s\up7(―→))＝eq \f(1,2)eq \(BC,\s\up7(―→))，则双曲线的离心率是( )
A.eq \r(2) B．eq \r(3)
C.eq \r(5) D．eq \r(10)
解析：选C 直线l：y＝－x＋a与渐近线l1：bx－ay＝0交于Beq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a2,a＋b)，\f(ab,a＋b)))，l与渐近线l2：bx＋ay＝0交于Ceq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a2,a－b)，\f(－ab,a－b)))，A(a,0)，
所以eq \(AB,\s\up7(―→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(ab,a＋b)，\f(ab,a＋b)))，eq \(BC,\s\up7(―→))＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2a2b,a2－b2)，－\f(2a2b,a2－b2)))，
因为eq \(AB,\s\up7(―→))＝eq \f(1,2)eq \(BC,\s\up7(―→))，所以b＝2a，所以c2－a2＝4a2，所以e2＝eq \f(c2,a2)＝5，所以e＝eq \r(5)，故选C.
2．设F1，F2分别为离心率e＝eq \r(5)的双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1eq \b\lc\(\rc\)(\a\vs4\al\c1(a>0，b>0))的左、右焦点，A1，A2分别为双曲线C的左、右顶点，以F1，F2为直径的圆交双曲线的渐近线l于M，N两点，若四边形MA2NA1的面积为4，则b＝( )
A．2 B．2eq \r(2)
C．4 D．4eq \r(2)
解析：选A 由e＝eq \r(5)＝eq \f(c,a)，得eq \f(b,a)＝2，故渐近线方程为y＝2x, 以F1，F2为直径的圆的方程为x2＋y2＝c2，联立eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋y2＝c2，,y＝2x，))得y＝±eq \f(2c,\r(5))，由双曲线与圆的对称性知四边形MA2NA1为平行四边形，不妨设yM＝eq \f(2c,\r(5))，则四边形MA2NA1的面积S＝2a×eq \f(2c,\r(5))＝4，得ac＝eq \r(5)，又eq \r(5)＝eq \f(c,a)，得a＝1，c＝eq \r(5)，b＝2，故选A.
3．(多选)已知动点P在双曲线C：x2－eq \f(y2,3)＝1上，双曲线C的左、右焦点分别为F1，F2，下列结论正确的是( )
A．C的离心率为2
B．C的渐近线方程为y＝±eq \f(\r(3),3)x
C．动点P到两条渐近线的距离之积为定值
D．当动点P在双曲线C的左支上时，eq \f(|PF1|,|PF2|2)的最大值为eq \f(1,4)
解析：选AC 对于双曲线C：x2－eq \f(y2,3)＝1，a＝1，b＝eq \r(3)，c＝2,
所以双曲线C的离心率为e＝eq \f(c,a)＝2，渐近线方程为y＝±eq \r(3)x，A选项正确，B选项错误；
设点P的坐标为(x0，y0)，则xeq \\al(2,0)－eq \f(y\\al(2,0),3)＝1，双曲线C的两条渐近线方程分别为x－eq \f(\r(3),3)y＝0和x＋eq \f(\r(3),3)y＝0，
则点P到两条渐近线的距离之积为eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(x0－\f(\r(3),3)y0)),\r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(－\f(\r(3),3)))2))·eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(x0＋\f(\r(3),3)y0)),\r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),3)))2))＝eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(x\\al(2,0)－\f(y\\al(2,0),3))),\f(4,3))＝eq \f(3,4)，C选项正确；
当动点P在双曲线C的左支上时，|PF1|≥c－a＝1，|PF2|＝2a＋|PF1|＝|PF1|＋2，
所以eq \f(|PF1|,|PF2|2)＝eq \f(|PF1|,|PF1|＋22)＝eq \f(|PF1|,|PF1|2＋4＋4|PF1|)＝eq \f(1,|PF1|＋\f(4,|PF1|)＋4)≤eq \f(1,2 \r(|PF1|·\f(4,|PF1|))＋4)＝eq \f(1,8)，
当且仅当|PF1|＝2时，等号成立，所以eq \f(|PF1|,|PF2|2)的最大值为eq \f(1,8)，D选项错误．故选A、C.标准方程
eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)
eq \f(y2,a2)－eq \f(x2,b2)＝1(a＞0，b＞0)
图形
性 质
范围
x≤－a或x≥a，y∈R
y≤－a或y≥a，x∈R
对称性
对称轴：坐标轴，对称中心：原点
顶点
A1(－a,0)，A2(a,0)
A1(0，－a)，A2(0，a)
渐近线
y＝±eq \f(b,a)x
y＝±eq \f(a,b)x
离心率
e＝eq \f(c,a)，e∈(1，＋∞)
实虚轴
线段A1A2是双曲线的实轴，它的长|A1A2|＝2a；
线段B1B2是双曲线的虚轴，它的长|B1B2|＝2b；
a是双曲线的实半轴长，b是双曲线的虚半轴长
a，b，c
的关系
c2＝a2＋b2(c＞a＞0，c＞b＞0)
类型一
与双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1有公共渐近线的双曲线方程可设为eq \f(x2,a2)－eq \f(y2,b2)＝λ(λ≠0)
类型二
若已知双曲线的一条渐近线方程为y＝eq \f(b,a)x或y＝－eq \f(b,a)x，则可设双曲线方程为eq \f(x2,a2)－eq \f(y2,b2)＝λ(λ≠0)
类型三
与双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1共焦点的双曲线方程可设为eq \f(x2,a2－k)－eq \f(y2,b2＋k)＝1(－b2＜k＜a2)
类型四
过两个已知点的双曲线的标准方程可设为eq \f(x2,m)－eq \f(y2,n)＝1(mn＞0)或者eq \f(x2,m)＋eq \f(y2,n)＝1(mn＜0)
类型五
与椭圆eq \f(x2,a2)＋eq \f(y2,b2)＝1(a＞b＞0)有共同焦点的双曲线方程可设为eq \f(x2,a2－λ)－eq \f(y2,λ－b2)＝1(b2＜λ＜a2)