高教版（2021·十四五）拓展模块一（上册）第2章 平面向量2.1 向量的概念精品ppt课件

这是一份高教版（2021·十四五）拓展模块一（上册）第2章 平面向量2.1 向量的概念精品ppt课件，共28页。PPT课件主要包含了情境导入，探索新知，典型例题，巩固练习，归纳总结，布置作业等内容，欢迎下载使用。

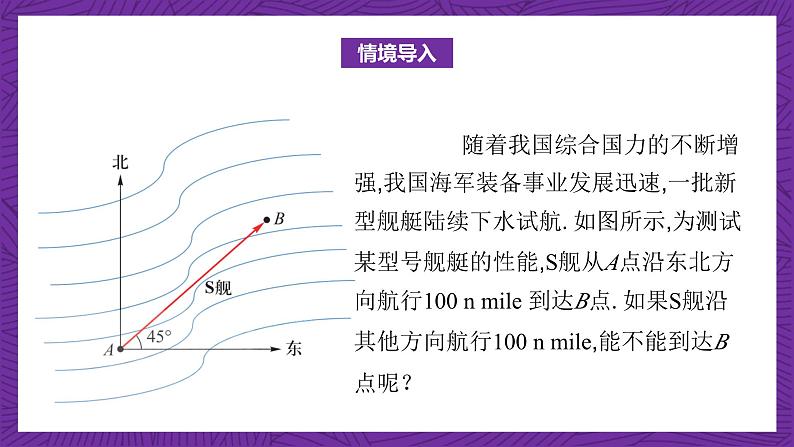
随着我国综合国力的不断增强,我国海军装备事业发展迅速,一批新型舰艇陆续下水试航. 如图所示,为测试某型号舰艇的性能,S舰从A点沿东北方向航行100 n mile 到达B点. 如果S舰沿其他方向航行100 n mile,能不能到达B点呢？
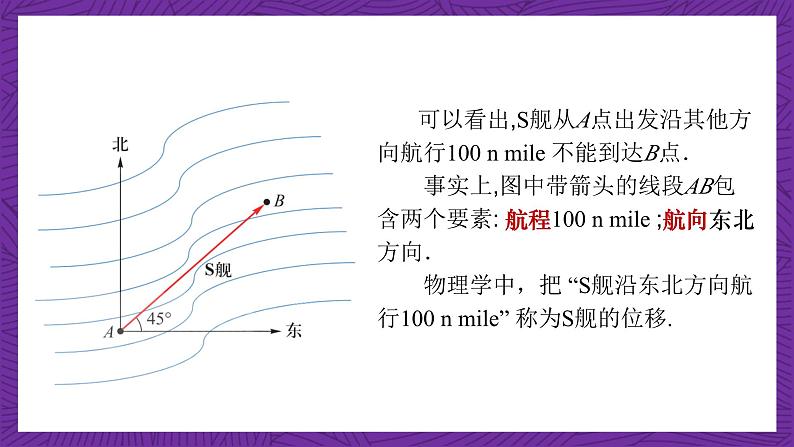
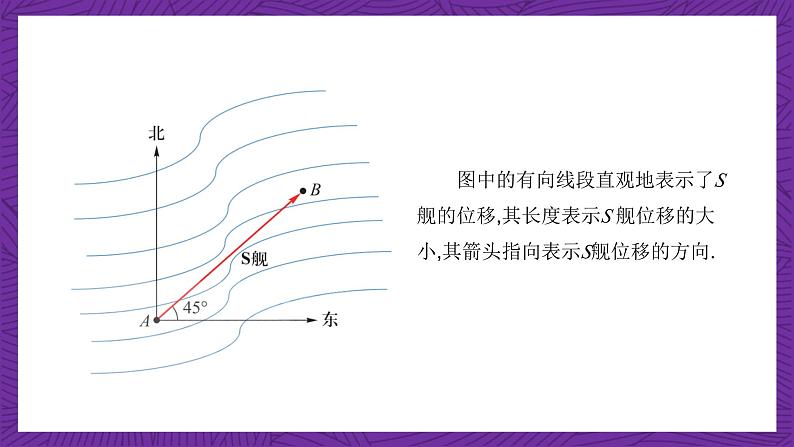
可以看出,S舰从A点出发沿其他方向航行100 n mile 不能到达B点． 事实上,图中带箭头的线段AB包含两个要素: 航程100 n mile ;航向东北方向． 物理学中，把 “S舰沿东北方向航行100 n mile” 称为S舰的位移.
生活和学习中常会遇到一些量，如长度、质量、时间、温度、面积、年龄，它们在给定了单位后，用一个实数就可以表示出来，这样的量称为数量．
非零向量的方向如何表示呢？
例2中的下列四组向量,每组的两个向量之间有什么关系？（1）i与j； （2）a与d；（3）a与b；（4）c与d.
向量i与j的模相等,但是方向不同,它们是不同的向量. 向量a与d的模不相等,但是方向相同,它们也是不同的向量. 向量a与b不仅模相等,而且方向相同.考虑到向量是由大小和方向所确定的,我们把 a与b看作一样的向量. 向量c与d的模相等,方向相反,它们的关系类似于相反数的关系.
一般地,模相等且方向相同的两个向量称为相等向量.向量a与b相等时,记a=b.
与非零向量a的模相等、方向相反的向量称为a的相反向量,记作−a.
规定：零向量的相反向量仍是零向量.
进一步观察还可以发现，向量a与d的方向相同,向量c与d的方向相反,但这两组向量有一个共性，即两个向量所在的直线平行.
一般地,方向相同或相反的两个向量称为平行向量.当向量a与b平行时,记a∥b.
规定：零向量与任何一个向量平行，即对于任意向量a,都有0∥a.
1.书面作业：完成课后习题和《学习指导与练习》；2.查漏补缺：根据个人情况对课堂学习复习与回顾;3.拓展作业：阅读教材扩展延伸内容.