新高考数学二轮复习讲义专题05 各类基本初等函数（二次函数、指对幂函数等）（2份打包，原卷版+解析版）

这是一份新高考数学二轮复习讲义专题05 各类基本初等函数（二次函数、指对幂函数等）（2份打包，原卷版+解析版），文件包含新高考数学二轮复习讲义专题05各类基本初等函数二次函数指对幂函数等原卷版doc、新高考数学二轮复习讲义专题05各类基本初等函数二次函数指对幂函数等解析版doc等2份试卷配套教学资源，其中试卷共49页， 欢迎下载使用。

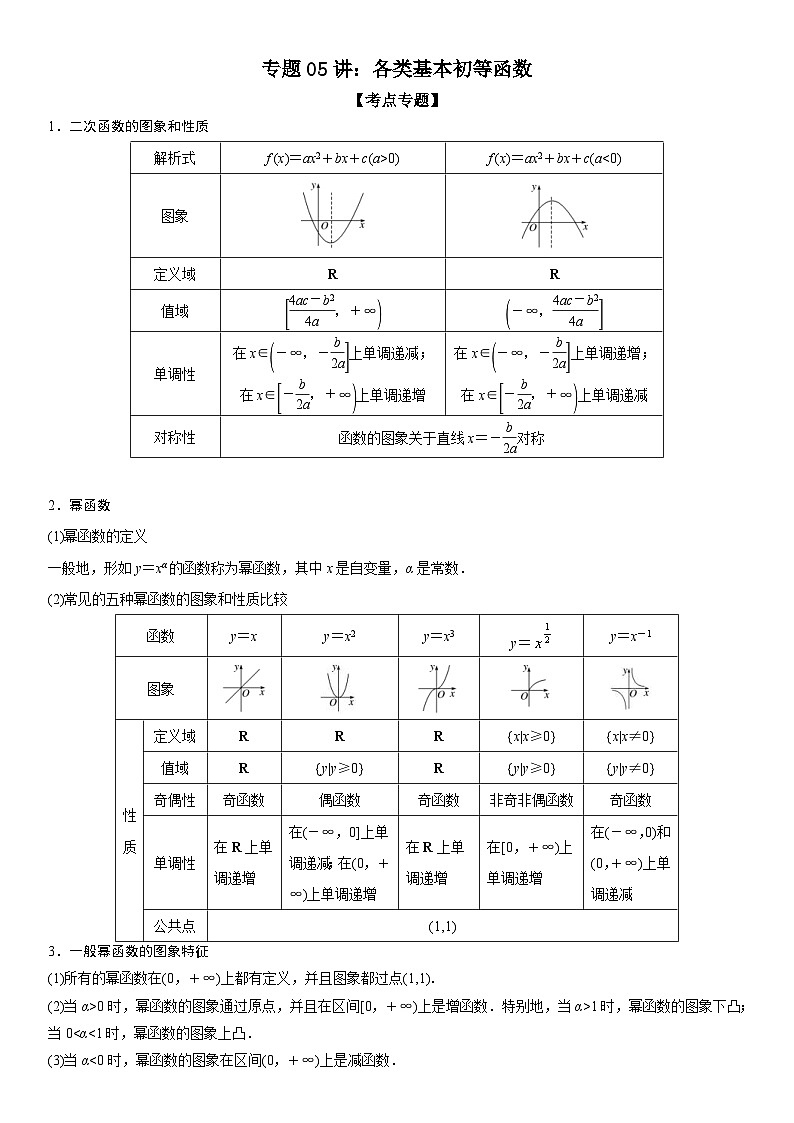
1．二次函数的图象和性质
2．幂函数
(1)幂函数的定义
一般地，形如y＝xα的函数称为幂函数，其中x是自变量，α是常数．
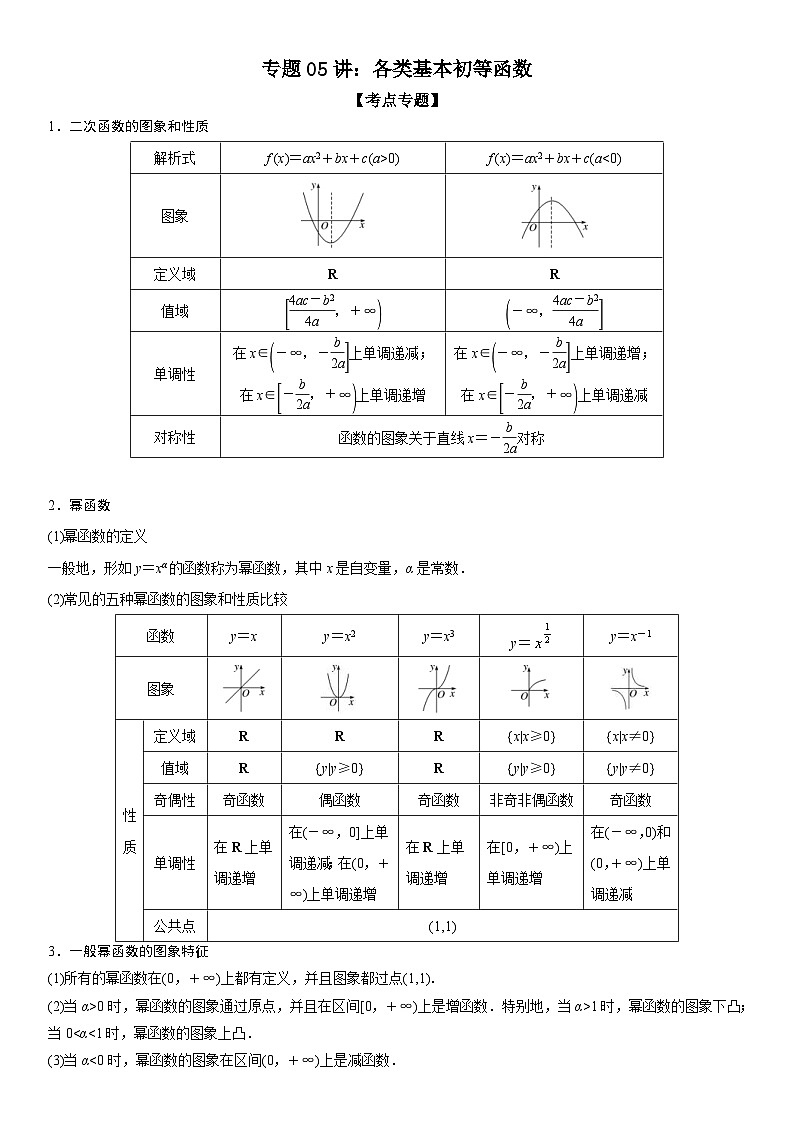
(2)常见的五种幂函数的图象和性质比较
3．一般幂函数的图象特征
(1)所有的幂函数在(0，＋∞)上都有定义，并且图象都过点(1,1)．
(2)当α>0时，幂函数的图象通过原点，并且在区间[0，＋∞)上是增函数．特别地，当α>1时，幂函数的图象下凸；当0<α<1时，幂函数的图象上凸．
(3)当α<0时，幂函数的图象在区间(0，＋∞)上是减函数．
(4)幂指数互为倒数的幂函数在第一象限内的图象关于直线y＝x对称．
(5)在第一象限作直线x＝a(a>1)，它同各幂函数图象相交，按交点从下到上的顺序，幂指数按从小到大的顺序排列．
4．分数指数幂
(1) SKIPIF 1 < 0 ＝eq \r(n,am)(a>0，m，n∈N*，且n>1)； SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 (a>0，m，n∈N*，且n>1)；
0的正分数指数幂等于0；0的负分数指数幂没有意义．
(2)有理数指数幂的运算性质(a>0，b>0，r，s∈R)
aras＝ar＋s； SKIPIF 1 < 0 ； (ar)s＝ars； (ab)r＝arbr ．
5．指数函数的图象与性质
6．对数的概念
一般地，如果ax＝N(a>0，且a≠1)，那么数x叫做以a为底N的对数，记作x＝lgaN，其中a叫做对数的底数，
N叫做真数．
以10为底的对数叫做常用对数，记作lg N.
以e为底的对数叫做自然对数，记作ln N. (e＝2.718 28…)
7．对数的性质与运算性质
(1)对数的性质：
= 1 \* GB3 \* MERGEFORMAT ①1的对数为零：lga1＝0.
= 2 \* GB3 \* MERGEFORMAT ②底的对数为1：lgaa＝1.
= 3 \* GB3 \* MERGEFORMAT ③零和负数没有对数．
= 4 \* GB3 \* MERGEFORMAT ④ SKIPIF 1 < 0 ＝N(a>0，且a≠1，N>0)．
(2)对数的运算性质
如果a>0，且a≠1，b>0，M>0，N>0，那么：
①lga(MN)＝lgaM＋lgaN；
②lgaeq \f(M,N)＝lgaM－lgaN；
③ SKIPIF 1 < 0 ＝eq \f(m,n)lgab．
(3)换底公式：lgab＝eq \f(lgcb,lgca)(a>0，且a≠1，b>0，c>0，且c≠1)．
重要推论： = 1 \* GB3 \* MERGEFORMAT ①lgaN＝eq \f(1,lgNa)(N>0，且N≠1；a>0，且a≠1)；
= 2 \* GB3 \* MERGEFORMAT ②lgab·lgbc·lgcd＝lgad(a>0，b>0，c>0，d>0，且a≠1，b≠1，c≠1)．
8．对数函数的图象与性质
9．反函数
指数函数y＝ax(a>0且a≠1)与对数函数y＝lgax(a>0且a≠1)互为反函数，它们的图象关于直线y＝x对称．
【方法技巧】
1．解决二次函数图象与性质问题时要注意：
(1)抛物线的开口方向，对称轴位置，定义区间三者相互制约，要注意分类讨论．
(2)要注意数形结合思想的应用，尤其是给定区间上的二次函数最值问题，先“定性”(作草图)，再“定量”(看图求解)．
(3)二次函数在闭区间上的最值主要有三种类型：轴定区间定、轴动区间定、轴定区间动．无论哪种类型，解题的关键都是图象的对称轴与区间的位置关系，当含有参数时，要依据图象的对称轴与区间的位置关系进行分类讨论．
2．幂函数：(1)幂函数的形式是y＝xα(α∈R)，其中只有一个参数α，因此只需一个条件即可确定其解析式．
(2)在区间(0,1)上，幂函数中指数越大，函数图象越靠近x轴(简记为“指大图低”)，在区间(1，＋∞)上，幂函数中指数越大，函数图象越远离x轴．
(3)对于幂函数图象的掌握只要抓住在第一象限内三条线分第一象限为六个区域，即x＝1，y＝1，y＝x所分区域．根据α<0,0<α<1，α＝1，α>1的取值确定位置后，其余象限部分由奇偶性决定．
(4)在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较，准确掌握各个幂函数的图象和性质是解题的关键．
3．指数函数：(1)利用指数函数的函数性质比较大小或解方程、不等式，最重要的是“同底”原则，比较大小还可以借助中间量；(2)求解与指数函数有关的复合函数问题，要明确复合函数的构成，涉及值域、单调区间、最值等问题时，都要借助“同增异减”这一性质分析判断．
4．对数运算的一般思路
(1)拆：首先利用幂的运算把底数或真数进行变形，化成分数指数幂的形式，使幂的底数最简，然后利用对数运算性质化简合并．
(2)合：将对数式化为同底数的和、差、倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幂的运算．
5．对数函数：(1)比较指数式和对数式的大小，可以利用函数的单调性，引入中间量；有时也可用数形结合的方法．
(2)解题时要根据实际情况来构造相应的函数，利用函数单调性进行比较，如果指数相同，而底数不同则构造幂函数，若底数相同而指数不同则构造指数函数，若引入中间量，一般选0或1.
(3)利用对数函数的性质，求与对数函数有关的函数值域和复合函数的单调性问题，必须弄清三方面的问题：一是定义域，所有问题都必须在定义域内讨论；二是底数与1的大小关系；三是复合函数的构成，即它是由哪些基本初等函数复合而成的．另外，解题时要注意数形结合、分类讨论、转化与化归思想的应用．
【核心题型】
题型一：二次函数的图像和性质
命题点1 二次函数的单调性
1．（2021·重庆市实验中学高三阶段练习）已知函数 SKIPIF 1 < 0 ，若函数 SKIPIF 1 < 0 在R上为减函数，则实数a的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2022·天津·耀华中学高三阶段练习）已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的增区间为（ ）
A．（–∞，–1）B．（–3，–1）
C．[–1，+∞）D．[–1，1）
3．（2015·四川·高考真题（理））如果函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上单调递减，
则mn的最大值为（ ）
A．16B．18C．25D． SKIPIF 1 < 0
命题点2 二次函数的值域、最值
4．（2023·全国·高三专题练习）若函数 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．（2022·江苏·阜宁县东沟中学高三阶段练习）已知直线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2022·安徽·合肥双凤高级中学模拟预测（文））已知圆 SKIPIF 1 < 0 与圆 SKIPIF 1 < 0 的公共弦所在直线恒过点 SKIPIF 1 < 0 ，且点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
命题点3 二次函数的恒（能）成立问题
7．（2019·云南师大附中高三阶段练习（文））若关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 的解集为实数集 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
8．（2021·江西·高三阶段练习（理））已知f(x)＝x2，g(x)＝ SKIPIF 1 < 0 －m，若对任意x1∈[0,2]，存在x2∈[1,2]，使得f(x1)≥g(x2)，则实数m的取值范围是________.
9．（2021·上海市吴淞中学高三阶段练习）已知函数 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时，都有 SKIPIF 1 < 0 恒成立，则 SKIPIF 1 < 0 _________.
题型二：幂函数的图像和性质
10．（2022·北京二十中高一阶段练习）在同一坐标系内，函数 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的图象可能是( )
A．B．C．D．
11．（2022·江苏·启东中学高三阶段练习）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
12．（2021·湖南·长沙一中高三阶段练习）已知函数 SKIPIF 1 < 0 ，若当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 恒成立，则实数a的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型三：指数函数的性质及应用
13．（2022·宁夏六盘山高级中学高三阶段练习（理））函数 SKIPIF 1 < 0 的大致图象为（ ）
A．B．
C．D．
14．（2022·安徽·安庆市第九中学高三阶段练习）已知函数 SKIPIF 1 < 0 ，满足对任意的实数 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 成立，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
15．（2023·全国·高三专题练习）已知函数 SKIPIF 1 < 0 ，若方程 SKIPIF 1 < 0 有解，则实数 SKIPIF 1 < 0 的取值范围是_________．
题型四：对数函数的性质及应用
16．（2010·全国·高三阶段练习（理））函数 SKIPIF 1 < 0 的值域是（ ）.
A．RB． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
17．（2021·湖北·襄阳四中高三阶段练习）地震的震级R与地震释放的能量E的关系为R＝ SKIPIF 1 < 0 (lgE－11.4).2011年3月11日，日本东海岸发生了9.级特大地震，2008年中国汶川的地震级别为8.0级，那么2011年地震的能量是2008年地震能量的__________倍．
18．（2021·天津·南开中学高三阶段练习）若函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是增函数，则实数 SKIPIF 1 < 0 的取值范围是______．
题型五：比较指数式、对数式的大小
19．（2022·全国·高三专题练习）已知函数 SKIPIF 1 < 0 则下述关系式正确的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
20．（2022·甘肃·高台县第一中学高三阶段练习（文））设 SKIPIF 1 < 0 是定义域为 SKIPIF 1 < 0 的偶函数，且在 SKIPIF 1 < 0 单调递增，设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
21．（2022·北京·北师大二附中高三阶段练习）已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的大小关系为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【高考必刷】
一、单选题
1．（2022·天津市武清区杨村第一中学高三阶段练习）已知函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是单调函数，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（2021·宁夏·青铜峡市宁朔中学高三阶段练习（文））已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则a，b，c的大小关系为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．（2021·广西·玉林市育才中学高三阶段练习（理））函数 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4．（2017·湖南·长郡中学高三阶段练习（理））幂函数 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 取不同的正数时，在区间 SKIPIF 1 < 0 上它们的图象是一簇曲线（如图）.设点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，连接AB，线段AB恰好被其中的两个幂函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的图象三等分，即有 SKIPIF 1 < 0 ，则mn等于（ ）
A．1B．2C．3D．无法确定
5．（2020·陕西西安·高三阶段练习（理））定义新运算“ SKIPIF 1 < 0 ”如下： SKIPIF 1 < 0 ，已知函数 SKIPIF 1 < 0 ，则满足 SKIPIF 1 < 0 的实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2021·江苏省镇江中学高三阶段练习）满足 SKIPIF 1 < 0 的实数m的取值范围是（ ）.
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
7．（2022·北京·人大附中高三阶段练习）设 SKIPIF 1 < 0 ，则“函数 SKIPIF 1 < 0 的图象经过点 SKIPIF 1 < 0 ”是“函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上递减”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
8．（2020·全国·高三课时练习（理））若 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
9．（2019·上海市吴淞中学高三开学考试）已知 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 在同一坐标系中的图象可能是
A．B．C．D．
10．（2022·甘肃·兰州市第五十五中学高三开学考试（文））函数 SKIPIF 1 < 0 的图象大致为（ ）
A．B．
C． D．
11．（2022·辽宁葫芦岛·高三期中）函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ）的图象恒过定点 SKIPIF 1 < 0 ，若点 SKIPIF 1 < 0 在椭圆 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）上，则 SKIPIF 1 < 0 的最小值为（ ）
A．12B．14C．16D．18
12．（2020·安徽·高三阶段练习（文））已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，以下命题：①若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；②若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；③若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；④若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 .其中正确的个数是（ ）
A．1B．2C．3D．4
13．（2022·江苏·高邮市第一中学高三阶段练习）已知55<84，134<85．设a=lg53，b=lg85，c=lg138，则（ ）
A．a14．（2017·辽宁·东北育才学校高三阶段练习（文））已知 SKIPIF 1 < 0 ，则下列不等式一定成立的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
15．（2020·湖南长沙·高三阶段练习（理））已知偶函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的大小关系为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
16．（2019·广东茂名·高三阶段练习（理））已知函数 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是
A．(1,2)B．(2,3)C．(1,3)D．(2,4)
17．（2022·全国·高三专题练习）若关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 在 SKIPIF 1 < 0 恒成立，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
18．（2019·天津市武清区杨村第一中学高三阶段练习）已知函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是增函数，且 SKIPIF 1 < 0 .若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
二、多选题
19．（2022·福建省漳平第二中学高三阶段练习）已知函数 SKIPIF 1 < 0 ，实数 SKIPIF 1 < 0 满足不等式 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
20．（2022·山东·巨野县实验中学高三阶段练习）若直线 SKIPIF 1 < 0 与函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ）的图象有两个公共点，则 SKIPIF 1 < 0 的取值可以是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．2
21．（2022·全国·高三专题练习）已知 SKIPIF 1 < 0 为定义在 SKIPIF 1 < 0 上的偶函数，当 SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 ，且当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .给出下列命题，其中正确的命题的为（ ）
A． SKIPIF 1 < 0
B．函数 SKIPIF 1 < 0 在定义域上是周期为2的周期函数
C．直线 SKIPIF 1 < 0 与函数 SKIPIF 1 < 0 的图像有1个交点
D．函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0
三、填空题
22．（2021·江西·高三阶段练习（文））设函数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，则 SKIPIF 1 < 0 的取值范围是__________．
23．（2020·江苏·高三专题练习）已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是__________.
24．（2022·全国·高三专题练习）已知函数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 对任意的 SKIPIF 1 < 0 恒成立，则实数 SKIPIF 1 < 0 的取值范围是___________.
25．（2022·安徽省怀宁县第二中学高三阶段练习）已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，对于存在 SKIPIF 1 < 0 ，存在 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是__________．
26．（2019·四川·高三阶段练习（理））如图，矩形 SKIPIF 1 < 0 的三个顶点 SKIPIF 1 < 0 分别在函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的图像上，且矩形的边分别平行于两坐标轴.若点 SKIPIF 1 < 0 的纵坐标为2，则点 SKIPIF 1 < 0 的坐标为______.
27．（2023·上海·高三专题练习）若 SKIPIF 1 < 0 ，且函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的图象恰有两个交点，则满足条件的不同集合 SKIPIF 1 < 0 有________个
28．（2023·全国·高三专题练习）写出一个同时具有下列性质①②③的函数： SKIPIF 1 < 0 ______．
① SKIPIF 1 < 0 为奇函数；
② SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减；
③当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
29．（2021·重庆市凤鸣山中学高三期中）已知函数 SKIPIF 1 < 0 ，若f(m)>1，则m的取值范围是________．
30．（2022·四川·树德中学高三阶段练习（文））已知函数 SKIPIF 1 < 0 ，则不等式 SKIPIF 1 < 0 的解集是______.
31．（2019·河北安平中学高三阶段练习（文））已知函数 SKIPIF 1 < 0 ，实数 SKIPIF 1 < 0 、 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的最大值是 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为______.
四、解答题
32．（2022·黑龙江·牡丹江一中高一阶段练习）设函数 SKIPIF 1 < 0 .
（1）若对于一切实数x， SKIPIF 1 < 0 恒成立，求实数m的取值范围；
（2）若对于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 恒成立，求实数m的取值范围.
33．（2023·江西·贵溪市实验中学高三阶段练习（理））已知幂函数 SKIPIF 1 < 0 的定义域为R.
(1)求实数 SKIPIF 1 < 0 的值；
(2)若函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上不单调，求实数 SKIPIF 1 < 0 的取值范围.
34．（2021·陕西·子长市中学高三阶段练习（文））已知函数 SKIPIF 1 < 0 .
(1)若函数 SKIPIF 1 < 0 是偶函数，求 SKIPIF 1 < 0 的值；
(2)当 SKIPIF 1 < 0 时，若函数 SKIPIF 1 < 0 存在两个零点，求 SKIPIF 1 < 0 的取值范围.
35．（2022·江西·金溪一中高三阶段练习（理））已知函数 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的最大值；
(2)设函数 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ，若对任意 SKIPIF 1 < 0 ， SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的最大值与最小值的差不超过1，求a的取值范围．
解析式
f (x)＝ax2＋bx＋c(a>0)
f (x)＝ax2＋bx＋c(a<0)
图象
定义域
R
R
值域
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(4ac－b2,4a)，＋∞))
eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(4ac－b2,4a)))
单调性
在x∈eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递减；
在x∈eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递增
在x∈eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(b,2a)))上单调递增；
在x∈eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(b,2a)，＋∞))上单调递减
对称性
函数的图象关于直线x＝－eq \f(b,2a)对称
函数
y＝x
y＝x2
y＝x3
y＝ SKIPIF 1 < 0
y＝x－1
图象
性质
定义域
R
R
R
{x|x≥0}
{x|x≠0}
值域
R
{y|y≥0}
R
{y|y≥0}
{y|y≠0}
奇偶性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调性
在R上单调递增
在(－∞，0]上单调递减；在(0，＋∞)上单调递增
在R上单调递增
在[0，＋∞)上单调递增
在(－∞，0)和(0，＋∞)上单调递减
公共点
(1,1)
y＝ax
a>1
0图象
定义域
(1)R
值域
(2)(0，＋∞)
性质
(3)过定点(0,1)
(4)当x>0时，y>1；
当x<0时，0(5)当x>0时，0当x<0时，y>1
(6)在(－∞，＋∞)上是增函数
(7)在(－∞，＋∞)上是减函数
y＝lgax
a>1
0图象
定义域
(0，＋∞)
值域
R
性
质
过定点(1,0)，即x＝1时，y＝0
当x>1时，y>0；
当0当x>1时，y<0；
当00
在(0，＋∞)上是增函数
在(0，＋∞)上是减函数