湖北省襄阳市2021_2022学年高一数学下学期6月月考试卷

这是一份湖北省襄阳市2021_2022学年高一数学下学期6月月考试卷，共13页。试卷主要包含了 已知复数满足，则z的虚部是， 的值为， 下列命题中正确的有等内容，欢迎下载使用。

一､单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 已知复数满足，则z的虚部是（ ）
A. B. C. D.
2. 的值为（ ）
A. B. C. D.
3. 下列命题中正确的有
（1）；（2）；（3）；（4）
A. 1个B. 2个C. 3个D. 4个
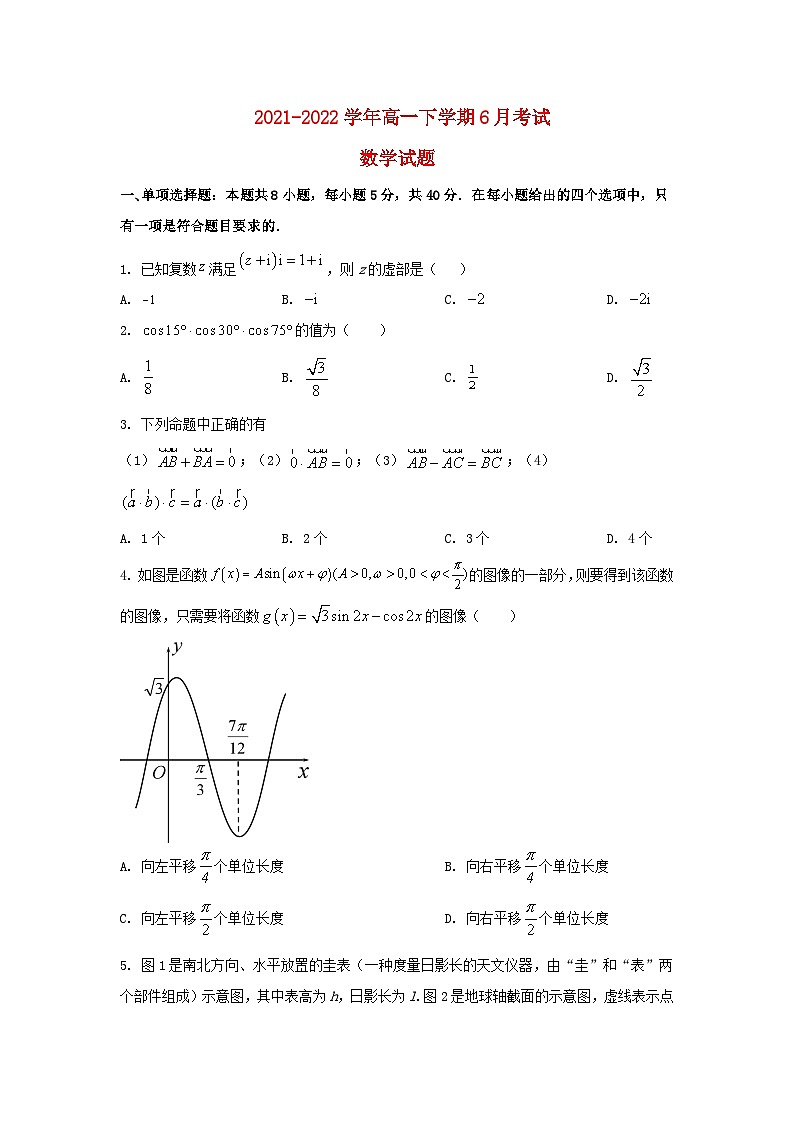
4. 如图是函数的图像的一部分，则要得到该函数的图像，只需要将函数的图像（ ）
A. 向左平移个单位长度B. 向右平移个单位长度
C. 向左平移个单位长度D. 向右平移个单位长度
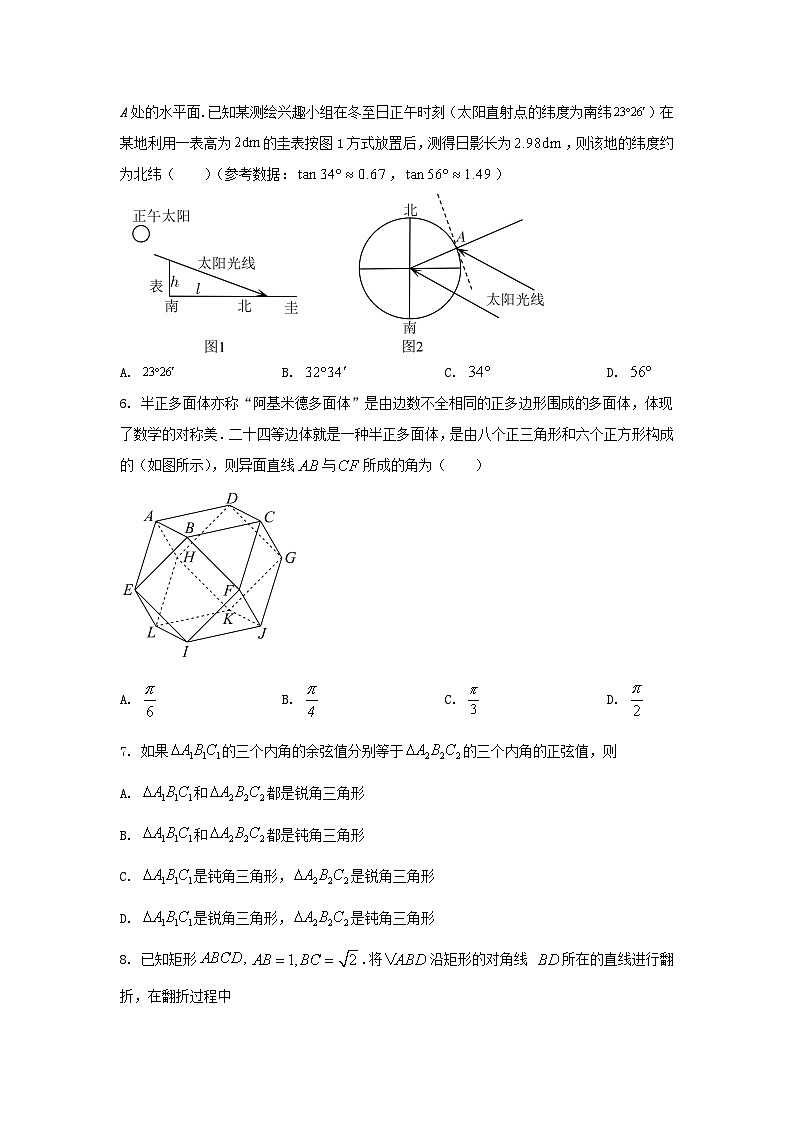
5. 图1是南北方向、水平放置的圭表（一种度量日影长的天文仪器，由“圭”和“表”两个部件组成）示意图，其中表高为h，日影长为l.图2是地球轴截面的示意图，虚线表示点A处的水平面.已知某测绘兴趣小组在冬至日正午时刻（太阳直射点的纬度为南纬）在某地利用一表高为的圭表按图1方式放置后，测得日影长为，则该地的纬度约为北纬（ ）（参考数据：，）
A. B. C. D.
6. 半正多面体亦称“阿基米德多面体”是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由八个正三角形和六个正方形构成的（如图所示），则异面直线与所成的角为（ ）
A. B. C. D.
7. 如果的三个内角的余弦值分别等于的三个内角的正弦值，则
A. 和都是锐角三角形
B. 和都是钝角三角形
C. 是钝角三角形，是锐角三角形
D. 是锐角三角形，是钝角三角形
8. 已知矩形．将沿矩形的对角线 所在的直线进行翻折，在翻折过程中
A. 存在某个位置，使得直线与直线 垂直
B. 存在某个位置，使得直线与直线 垂直
C. 存在某个位置，使得直线与直线 垂直
D. 对任意位置，三对直线“与 ”，“与 ”，“与 ”均不垂直
二､多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．
9. 如图是某市5月1日至10日PM2.5的日均值（单位：μg/m3）变化的折线图，关于PM2.5日均值说法错误的是（ ）
A. 这10天日均值的83%分位数为78；
B. 这10天的日均值的中位数为41；
C. 前5天的日均值的方差大于后5天的日均值的方差；
D. 前5天日均值的极差小于后5天的日均值的极差．
10. 八卦是中国文化的基本哲学概念，如图1船八卦模型图，其平面图形记为图2中的正八边形，其中，则下列结论正确的有（ ）
A. B.
C. D. 在向量上的投影向量的模为
11. 中，内角A，B，C的对边分别为a，b，c，，BC边上的中线，则下列说法正确的有：（ ）
A. B.
C. D. ∠BAD的最大值为60°
12. 如图，在多面体中，平面，四边形是正方形，且，，分别是线段的中点，是线段上的一个动点（含端点），则下列说法正确的是（ ）
A. 存在点，使得
B. 存在点，使得异面直线与所成角为
C. 三棱锥体积的最大值是
D. 当点自向处运动时，二面角平面角先变小后变大
三､填空题（本大题共4小题，每小题5分，共20分）
13. 为了考查某种小麦的长势，从中抽取10株麦苗，测得苗高（单位：cm）为16，9，14，11，12，10，16，8，17，19，则这组数据的极差是______．
14. 已知非零向量满足，且，则__________．
15. 在某高传染性病毒流行期间，为了建立指标显示疫情已受控制，以便向该地区居民显示可以过正常生活，有公共卫生专家建议指标是“连续7天每天新增感染人数不超过5人”，根据连续7天的新增病例数计算，下列各个选项中，一定符合上述指标的是__________(填写序号)．
①平均数； ②标准差； ③平均数且极差小于或等于2；
④平均数且标准差； ⑤众数等于1且极差小于或等于4．
16. 如图，在棱长为2的正方体中，点､分别是棱，的中点，是侧面内（不含边界）一点，若平面，则线段长度的最小值是___________.

四､解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）
17. 已知方程的两复数根分别为，，其中的虚部大于0
（1）求复数，；
（2）若复数，且，求实数的取值范围
18. 2022年2月8日，中国选手谷爱凌在北京冬奥会女子大跳台项目决赛中以之前从未有人在正式比赛中完成的“左转1620”动作一举夺得冠军，为中国代表团揽入一枚里程碑式的金牌．受奥运精神的鼓舞，某滑雪俱乐部组织100名滑雪爱好者进行了一系列的大跳台测试，并记录他们的动作得分（单位：分），将所得数据整理得到如图所示的频率分布直方图．
（1）求频率分布直方图中a的值；
（2）估计该100名射击爱好者的射击平均得分（求平均值时同一组数据用该组区间的中点值作代表）；
（3）该俱乐部计划招募成绩位列前10%的滑雪爱好者组成集训队备战明年的滑雪俱乐部联盟赛，请根据图中信息，估计集训队入围成绩（记为k）．
19. 如图，在三棱锥中，D，E分别为的中点，且平面．
（1）证明：；
（2）若，求锐二面角的大小．
20. 设的内角A、B、C所对的边分别为a、b、c，且的面积．
（1）求的值；
（2）若，求的取值范围．
21. 如图，在某景区依湖畔而建的半径为500米的一条圆弧形小路上，为吸引游客，景区在这条弧形小路上取两点A，B，准备分别以A，B两处为入口，在河岸内侧建造两条玻璃栈道，，并在两条栈道的终点P处建造一个观景台，已知弧所对的圆心角为.
（1）若为等腰直角三角形，且为斜边，求的面积；
（2）假设玻璃栈道的宽度固定，修建玻璃栈道的造价按照长度来计算，且造价为1200元/米，试问当时，修建两条玻璃栈道最多共需要多少万元？
22. 如图，四棱柱中，底面．四边形为梯形，，且．过三点的平面记为与的交点为．
（1）证明：为中点；
（2）求此四棱柱被平面所分成上下两部分的体积之比；
（3）若，梯形的面积为6，求平面与底面所成二面角大小．
答案
1-8 CBAAB CDB 9.BC 10.AB 11.ABC 12.AD
13. 11
14.
15. ③⑤
16.
17.（1）由，得，
所以，所以，
而的虚部大于0，所以，.
（2）由（1）中可知，
所以可化为，
即，
所以，解得，
即实数的取值范围是.
18.（1）由题意可得：，解得
（2）由题意可得：估计该100名射击爱好者的射击平均得分
（3）根据频率分布直方图可知：的频率为
设入围成绩的临界值为，则，即
估计集训队入围成绩
19.（1）∵D为中点，且，∴，即．
∵平面，平面，∴．
∵，∴平面．
又∵平面，∴；
（2）由（1）可知，以为x轴，为y轴，建立如图所示的空间直角坐标系．
设，∵，∴，，
∴．
设平面的法向量为，有
即，令，得．
设平面的法向量为，
由，
有，取，则
可得，
有，，
∴二面角的余弦值为，
故锐二面角的大小为．
20.（1）由余弦定理得：①，
②，两式相减得：
，
因为，
所以，
即，
由正弦定理得：
因为，所以，且，
故，即.
（2）由（1）知：，
因为，所以，，
所以，
又因为，
所以，
所以.
21.（1）因为弧所对的圆心角为，圆的半径为500，所以米，
又为等腰直角三角形，且为斜边，所以米，
所以的面积为平方米.
（2）设，，
由正弦定理得，得，
由正弦定理得，得，
所以
，
因为，所以，
所以当，即时，取得最大值为米，
所以修建两条玻璃栈道最多共需要万元.
22.（1）证明：四棱柱中，四边形为梯形，，
平面平面，
平面与面和平面的交线平行，
，
，
为的中点；
（2）
解：连接，设，
梯形的高为，
四棱柱被平面所分成上､下两部分的体积为，
设，则，
，
，
棱柱，
四棱柱被平面所分成上､下两部分的体积之比
（3）解：在中，作，垂足为，连接，
则平面，
，
为平面与底面所成二面角平面角，
，
，
梯形的面积为，
，
，
，
平面与底面所成二面角的大小为．