



- 新高考数学一轮复习(举一反三)重难点题型精练专题2.5 函数的奇偶性(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习(举一反三)重难点题型精练专题2.7 函数的周期性与对称性(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习(举一反三)重难点题型精练专题2.10 幂函数与二次函数(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习(举一反三)重难点题型精练专题2.11 指数与指数函数(2份打包,原卷版+解析版) 试卷 0 次下载
- 新高考数学一轮复习(举一反三)重难点题型精练专题2.12 指数与指数函数(2份打包,原卷版+解析版) 试卷 0 次下载
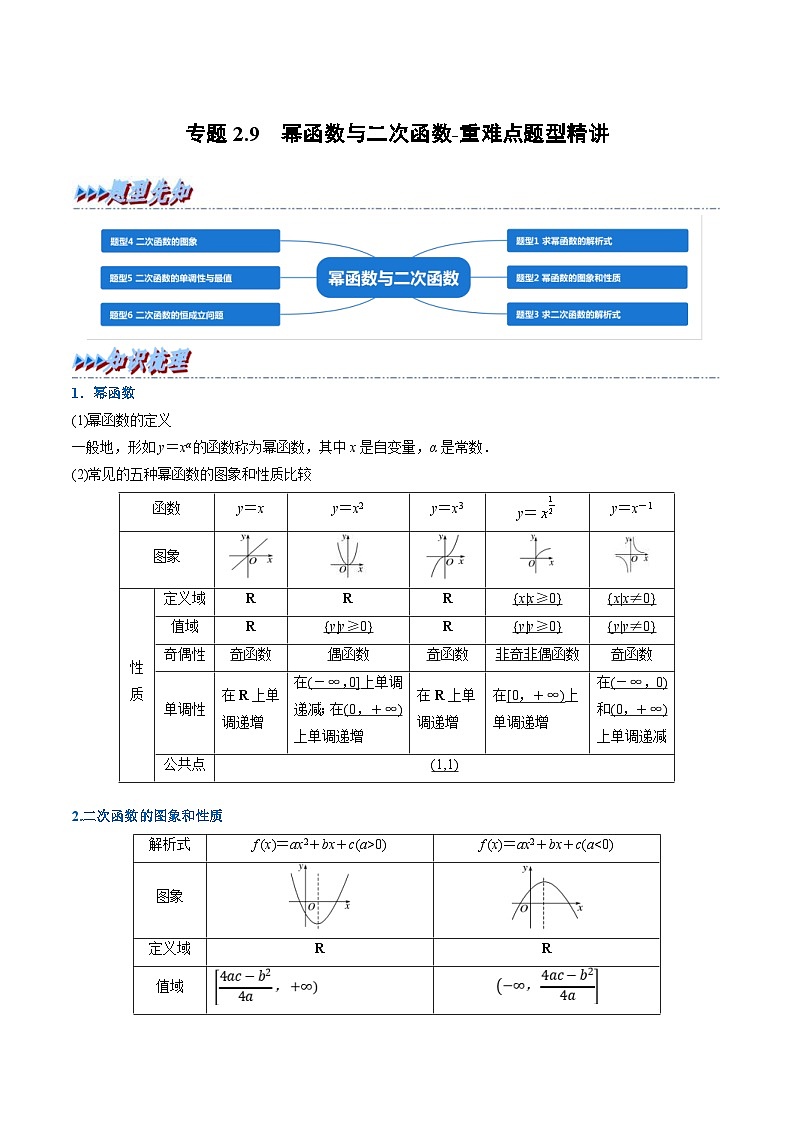
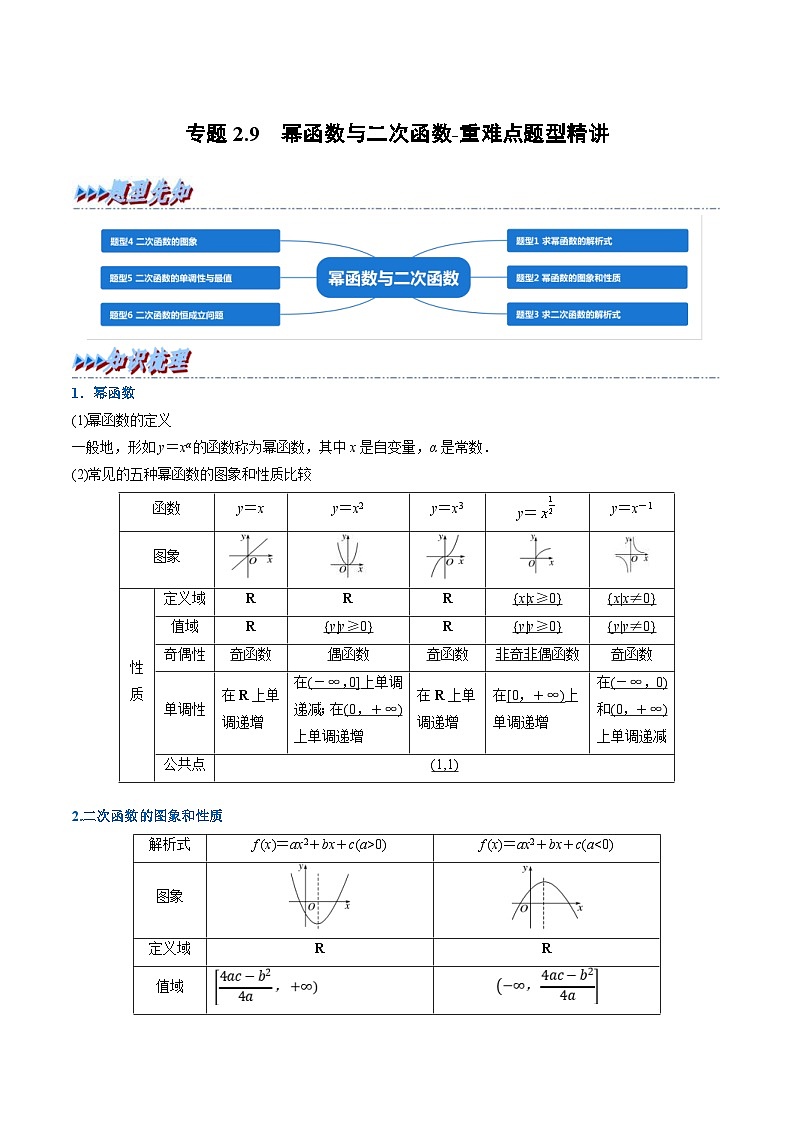
新高考数学一轮复习(举一反三)重难点题型精练专题2.9 幂函数与二次函数(2份打包,原卷版+解析版)
展开1.幂函数
(1)幂函数的定义
一般地,形如y=xα的函数称为幂函数,其中x是自变量,α是常数.
(2)常见的五种幂函数的图象和性质比较
2.二次函数的图象和性质
【题型1 求幂函数的解析式】
(1)判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:①指数为常数;②底数为自变量;③系数为1.
(2)对于幂函数过已知的某一点,求幂函数解析式问题:先设出幂函数的解析式y=xα(α为常数),再将已知点代入解析式,求出α,即可得出解析式.
【例1】(2021秋•临渭区期末)已知幂函数y=f(x)的图像过点(2,8),则f(﹣2)的值为( )
A.8B.﹣8C.4D.﹣4
【解题思路】设所求的幂函数为f(x)=xa,由幂函数y=f(x)的图象经过点(2,8),解得f(x)=x3,由此能求出f(﹣2)的值.
【解答过程】解:设所求的幂函数为f(x)=xa,
∵幂函数y=f(x)的图象经过点(2,8),
∴f(2)=2a=8,解得a=3,
∴f(x)=x3,
∴f(﹣2)=(﹣2)3=﹣8,
故选:B.
【变式1-1】(2021秋•阳春市校级月考)已知幂函数y=f(x)的图象过点,则f(4)的值为( )
A.﹣2B.1C.2D.4
【解题思路】设幂函数的解析式为f(x)=xα,代入点可求α的值,从而可求f(4)的值.
【解答过程】解:设幂函数的解析式为f(x)=xα,
因为幂函数y=f(x)的图象过点,所以3α,解得α.
所以f(x),f(4)2.
故选:C.
【变式1-2】(2022春•无锡期末)已知幂函数y=f(x)的图像过点,则f(16)=( )
A.B.C.﹣4D.4
【解题思路】设出函数的解析式,代入点的坐标,求出函数f(x)的解析式,求出函数值即可.
【解答过程】解:令f(x)=xα,
将点代入函数的解析式得:
2α,解得α,
故f(x),f(16),
故选:B.
【变式1-3】(2022春•广陵区校级月考)若幂函数f(x)=xa的图象经过点,则函数f(x)的解析式是( )
A.B.C.D.
【解题思路】由题意,利用幂函数的定义和性质,用待定系数法求出它的解析式.
【解答过程】解:∵幂函数f(x)=xa的图象经过点,
∴2a,解得,∴,
故选:A.
【题型2 幂函数的图象和性质】
(1)幂函数的形式是y=xα(α∈R),其中只有一个参数α,因此只需一个条件即可确定其解析式.
(2)在区间(0,1)上,幂函数中指数越大,函数图象越靠近x轴(简记为“指大图低”),在区间(1,+∞)上,幂函
数中指数越大,函数图象越远离x轴.
(3)在比较幂值的大小时,必须结合幂值的特点,选择适当的函数,借助其单调性进行比较,准确掌握各个
幂函数的图象和性质是解题的关键.
【例2】(2022春•德州期末)幂函数在区间(0,+∞)上单调递增,则f(3)=( )
A.27B.9C.D.
【解题思路】根据幂函数的概念及性质,求出实数m的值,得到幂函数的解析式,由此能求出结果.
【解答过程】解:∵幂函数在区间(0,+∞)上单调递增,
∴,
解得m=2,
∴f(x)=x3,
∴f(3)=33=27.
故选:A.
【变式2-1】(2022春•玉林期末)幂函数(0≤m≤3,m∈Z)的图象关于y轴对称,且在(0,+∞)上是增函数,则m的值为( )
A.0B.2C.3D.2和3
【解题思路】由题意可得m2+m﹣2>0,且m2+m﹣2为偶数,结合0≤m≤3,m∈Z,求出m的值.
【解答过程】解:由题意,可得m2+m﹣2>0,且m2+m﹣2为偶数,
∵0≤m≤3,m∈Z,∴m=2或3.
故选:D.
【变式2-2】(2021秋•鹿城区校级期中)已知幂函数f(x)的图象过点,若x1>x2>1,则( )
A.f(x1)>f(x2)>1B.f(x1)>1>f(x2)
C.f(x1)<f(x2)<1D.f(x1)<1>f(x2)
【解题思路】求出幂函数的解析式,根据幂函数的单调性,判断f(x1),1,f(x2)的大小即可.
【解答过程】解:幂函数f(x)的图象过点,所以,
所以α=﹣1,所以幂函数为y=x﹣1,幂函数在x>0时是减函数,
因为x1>x2>1,所以f(x1)<f(x2)<1.
故选:C.
【变式2-3】(2021秋•黟县校级期中)设α∈{﹣3,﹣2,﹣1,,,1,2,3},则使y=xα为奇函数且在(0,+∞)上单调递减的α值的个数为( )
A.1B.2C.3D.4
【解题思路】利用幂函数的性质、奇函数的定义、函数的单调性即可得出.
【解答过程】解:只有当α=﹣3,﹣1时,满足幂函数y=xa为奇函数且在(0,+∞)上单调递减.
故选:B.
【题型3 求二次函数的解析式】
求二次函数解析式的方法:
(1)已知三点坐标,选用一般式;
(2)已知顶点坐标、对称轴、最大(小)值等条件,选用顶点式;
(3)已知与x轴两交点坐标,选用零点式.
【例3】已知二次函数f(x)的图象经过两点(0,3),(2,3),且最大值是5,则该函数的解析式是( )
A.f(x)=2x2﹣8x+11B.f(x)=﹣2x2﹣8x﹣1
C.f(x)=2x2﹣4x+3D.f(x)=﹣2x2+4x+3
【解题思路】由题意可得对称轴x=1,最大值是5,故可设f(x)=a(x﹣1)2+5,代入其中一个点的坐标即可求出a的值,问题得以解决.
【解答过程】解:二次函数f(x)的图象经过两点(0,3),(2,3),则对称轴x=1,最大值是5,
可设f(x)=a(x﹣1)2+5,
于是3=a+5,解得a=﹣2,
故f(x)=﹣2(x﹣1)2+5=﹣2x2+4x+3,
故选:D.
【变式3-1】 二次函数y=ax2+bx+c,当y<0时,x的取值范围是x<﹣2或x>3,则二次函数的解析式是( )
A.y=x2﹣x﹣6B.y=x2+x﹣5C.y=﹣x2+x+6D.y=﹣2x2+3x
【解题思路】根据题意得出a<0,x=﹣2,x=3是ax2+bx+c=0的根,判断即可得出答案.
【解答过程】解:∵二次函数y=ax2+bx+c,当y<0时,x的取值范围是x<﹣2或x>3,
∴a<0,x=﹣2,x=3是ax2+bx+c=0的根,
A,B的开口向上,故不正确,
D的零点为0,,故不正确,
故选:C.
【变式3-2】(2021秋•增城市校级期中)已知二次函数的图象与x轴交于点(﹣1,0)和(2,0),且与y轴交于(0,﹣2),那么此函数的解析式是( )
A.y=﹣x2+x+2B.y=x2﹣x﹣2C.y=x2+x﹣2D.y=2x2﹣2x﹣4
【解题思路】由题意知,可用两根式设抛物线的解析式,然后将三点坐标代入抛物线的解析式中,即可求出待定系数的值.
【解答过程】解:由于二次函数的图象与x轴交于点(﹣1,0)和(2,0),
故可设这个二次函数的解析式是y=a(x+1)(x﹣2)(a≠0),
又由二次函数的图象与y轴交于(0,﹣2),则﹣2=a(0+1)(0﹣2)
解之得a=1;
所以该函数的解析式为:y=(x+1)(x﹣2)=x2﹣x﹣2
故选:B.
【变式3-3】(2022•山东模拟)二次函数f(x)的图象经过两点(0,3),(2,3)且最大值是5,则该函数的解析式是( )
A.f(x)=2x2﹣8x+11B.f(x)=﹣2x2+8x﹣1
C.f(x)=2x2﹣4x+3D.f(x)=﹣2x2+4x+3
【解题思路】由题意可得对称轴x=1,最大值是5,故可设f(x)=a(x﹣1)2+5,代入其中一个点的坐标即可求出a的值,问题得以解决
【解答过程】解:二次函数f(x)的图象经过两点(0,3),(2,3),则对称轴x=1,最大值是5,
可设f(x)=a(x﹣1)2+5,
于是3=a+5,解得a=﹣2,
故f(x)=﹣2(x﹣1)2+5=﹣2x2+4x+3,
故选:D.
【题型4 二次函数的图象】
(1)研究二次函数图象应从“三点一线一开口”进行分析;
(2)求解与二次函数有关的不等式问题,可借助二次函数的图象特征,分析不等关系成立的条件.
【例4】(2021秋•衢州期中)二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A.2a﹣b=0B.a+b+c<0C.a﹣b+c<0D.abc>0
【解题思路】由已知结合二次函数的图象及性质分析各选项即可判断.
【解答过程】解:由图象可知,a<0,c>0,1,
所以b=﹣2a,A错误;
因为f(﹣1)=a﹣b+c<0,C正确,f(1)=a+b+c>0,B错误;
所以abc<0,D错误.
故选:C.
【变式4-1】(2021秋•三元区校级月考)二次函数y=ax2+bx+c的图象如图所示,下列结论中:
①4ac<b2;②a+c>b;③2a+b>0.
其中正确的是( )
A.①②B.①③C.①②③D.②③
【解题思路】结合函数的图象以及二次函数的性质判断即可.
【解答过程】解:y=ax2+bx+c有2个零点,
故Δ=b2﹣4ac>0,故①正确,
结合图象f(﹣1)<0,故a﹣b+c<0,
故②错误,
函数对称轴是x1,(a<0),
故2a+b>0,故③正确,
故选:B.
【变式4-2】(2021秋•上蔡县校级月考)二次函数y=ax2+bx+c的图象如图所示,则下列结论中正确的是( )
①b=﹣2a;
②a+b+c<0;
③a﹣b+c>0;
④abc<0.
A.①③B.②③C.②④D.①④
【解题思路】结合图像,根据二次函数的性质分别判断即可.
【解答过程】解:结合图像,
对称轴x1,故b=﹣2a,故①正确;
f(1)=a+b+b>0,故②错误;
f(﹣1)=a﹣b+c<0,故③错误;
a<0,b>0,c>0,故abc<0,故④正确;
故选:D.
【变式4-3】(2020春•霍邱县校级期末)二次函数f(x)的图象如图所示,则f(x﹣1)<0的解集为( )
A.(﹣2,1)B.(0,3)
C.(﹣1,2)D.(﹣∞,0)∪(3,+∞)
【解题思路】由图象知,当﹣1<x<2时,则f(x)<0,再列出不等式即可.
【解答过程】解:由图象知,当﹣1<x<2时,则f(x)<0,
∵f(x﹣1)<0,
∴﹣1<x﹣1<2,
∴0<x<3,
∴不等式的解集为(0,3).
故选:B.
【题型5 二次函数的单调性与最值】
(1)二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动.不论哪种类型,
解题的关键都是对称轴与区间的位置关系,当含有参数时,要依据对称轴与区间的位置关系进行分类讨论.
(2)二次函数的单调性问题主要依据二次函数图象的对称轴进行分类讨论求解.
【例5】(2022春•兴庆区校级期末)函数y=x2﹣x+1,x∈[﹣1,1]的最大值与最小值之和为( )
A.1.75B.3.75C.4D.5
【解题思路】数y=x2﹣x+1,对称轴为x,y,f(﹣1)=3,f(1)=1,故最大值为3,最小值为0.75,求出即可.
【解答过程】解:函数y=x2﹣x+1,对称轴为x,
y,
f(﹣1)=3,f(1)=1,
故最大值为3,最小值为0.75
所以最大值和最小值的和为3.75,
故选:B.
【变式5-1】(2021秋•靖远县期中)已知函数f(x)=x2﹣4x在区间[﹣1,m]上的最大值为5,则实数m的取值范围是( )
A.(2,5]B.(﹣1,5]C.[2,5]D.(1,5]
【解题思路】根据题意,f(x)=x2﹣4x=(x﹣2)2﹣4的对称轴为x=2,且当x=2时,函数有最小值f(2)=﹣4,且f(﹣1)=f(5)=5,又函数f(x)=x2﹣4x在区间[﹣1,m]上的最大值为5,从而可得﹣1<m≤5.
【解答过程】解:根据题意,f(x)=x2﹣4x=(x﹣2)2﹣4的对称轴为x=2,
且当x=2时,函数有最小值f(2)=﹣4,
令f(x)=5,得x2﹣4x﹣5=0,解得x=﹣1或x=5,
∵函数f(x)=x2﹣4x在区间[﹣1,m]上的最大值为5,
∴﹣1<m≤5,即m的取值范围是(﹣1,5].
故选:B.
【变式5-2】(2021•天心区校级开学)二次函数f(x)满足f(2+x)=f(2﹣x),且f(x)在[0,2]上是减函数,若f(a)≤f(0),则实数a的取值范围为( )
A.[0,4]B.(﹣∞,0]
C.[0,+∞)D.(﹣∞,0]∪[4,+∞)
【解题思路】根据题意知f(x)的对称轴为x=2,由f(a)≤f (0)得出|a﹣2|≤2,从而求得a的取值范围.
【解答过程】解:函数f(x)满足f (2+x)=f (2﹣x),则f(x)的对称轴为x=2;
又f(x)在[0,2]上是减函数,则f(x)在[2,4]上是增函数;
如图所示,
若f(a)≤f (0),则有|a﹣2|≤2,
解得:0≤a≤4,
即a的取值范围是[0,4].
故选:A.
【变式5-3】(2022•东湖区校级模拟)已知二次函数f(x)=x2﹣2ax+5,若f(x)在区间(﹣∞,2]上是减函数,且对任意x1,x2∈[1,a+1],总有|f(x1)﹣f(x2)|≤4,则实数a的取值范围是( )
A.[2,3]B.[1,2]C.[﹣1,3]D.[2,+∞)
【解题思路】先由函数的解析式求出其对称轴及单调区间;然后根据f(x)在区间(﹣∞,2]上是减函数,得出a的一个取值范围;
再对任意的x1,x2∈[1,a+1],|f(x1)﹣f(x2)|max=|f(a)﹣f(1)|≤4,又可求出a的一个取值范围;最后两者取交集,则问题解决.
【解答过程】解:函数f(x)=x2﹣2ax+5的对称轴是x=a,则其单调减区间为(﹣∞,a],
因为f(x)在区间(﹣∞,2]上是减函数,所以2≤a,即a≥2.
则|a﹣1|≥|(a+1)﹣a|=1,
因此任意的x1,x2∈[1,a+1],总有|f(x1)﹣f(x2)|≤4,只需|f(a)﹣f(1)|≤4即可,
即|(a2﹣2a2+5)﹣(1﹣2a+5)|=|a2﹣2a+1|=(a﹣1)2≤4,亦即﹣2≤a﹣1≤2,
解得﹣1≤a≤3,又a≥2,
因此a∈[2,3].
故选:A.
【题型6 二次函数的恒成立问题】
【方法点拨】
(1)一般有两个解题思路:一是分离参数;二是不分离参数.
(2)两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否已分离.这两个思路的依据是:a≥f(x)恒成立⇔a≥f(x)max,a≤f(x)恒成立⇔a≤f(x)min.
【例6】(2020秋•宁波期末)已知函数f(x)=4ax2+4x﹣1,∀x∈(﹣1,1),f(x)<0恒成立,则实数a的取值范围是( )
A.B.a<﹣1C.D.a≤﹣1
【解题思路】对二次项系数a的取值进行分类讨论,分a=0,a>0,a<0三种情况分别求解,即可得到答案.
【解答过程】解:当a=0时,f(x)=4x﹣1<0,解得,
故当x时,f(x)>0,故不符合题意;
当a>0时,则有,无解;
当a<0时,则有①,或②,或Δ=16+16a<0③,
解得①无解,②无解,③a<﹣1,
故a<﹣1,
综上所述,实数a的取值范围是a<﹣1.
故选:B.
【变式6-1】(2020春•玉林期末)已知函数f(x)=x2+(4﹣k)x,若f(x)<k﹣2对x∈[1,2]恒成立,则k的取值范围为( )
A.(﹣∞,)B.(,+∞)C.(﹣∞,)D.(,+∞)
【解题思路】由题意可得x2+(4﹣k)x﹣k+2<0在x∈[1,2]恒成立,可设g(x)=x2+(4﹣k)x﹣k+2,结合y=g(x)的图象,只需g(1)<0,且g(2)<0,解不等式可得所求范围.
【解答过程】解:函数f(x)=x2+(4﹣k)x,若f(x)<k﹣2对x∈[1,2]恒成立,
可得x2+(4﹣k)x﹣k+2<0在x∈[1,2]恒成立,
可设g(x)=x2+(4﹣k)x﹣k+2,
由于y=g(x)的图象为开口向上的抛物线,只需g(1)<0且g(2)<0,
所以,即,
可得k.
故选:D.
【变式6-2】(2020秋•湖北期中)已知f(x)=x2+4x+1+a,∀x∈R,f(f(x))≥0恒成立,则实数a的取值范围为( )
A.B.[2,+∞)C.[﹣1,+∞)D.[3,+∞)
【解题思路】换元,令t=f(x),则t≥a﹣3,所以f(t)≥0对任意t≥a﹣3恒成立,再求出f(t)的最小值后,解不等式即可.
【解答过程】解:设t=f(x)=(x+2)2+a﹣3≥a﹣3,
∴f(t)≥0对任意t≥a﹣3恒成立,
即(t+2)2+a﹣3≥0对任意t∈[a﹣3,+∞)都成立,
①当a﹣3≤﹣2,即a≤1时,f(t)min=f(﹣2)=a﹣3,
则a﹣3≥0,即a≥3,与讨论a≤1矛盾,
②当a﹣3>﹣2,即a>1时,f(t)min=f(a﹣3)=a2﹣a﹣2≥0,
解得a≥2或a≤﹣1,∵a>1,∴a≥2,
∴实数a的取值范围为[2,+∞).
故选:B.
【变式6-3】(2021秋•上高县校级月考)已知二次函数f(x)满足f(x+1)=x2﹣x+2,若f(x)>3x+m在区间[﹣1,3]上恒成立,则实数m的范围是( )
A.m<﹣5B.m>﹣5C.m<11D.m>11
【解题思路】先令t=x+,则x=t﹣1,然后用换元法求出f(x)的解析式,再根据f(x)>3x+m对于x∈[﹣1,3]恒成立,转化为m<x2﹣6x+4对x∈[﹣1,3]恒成立,再确定g(x)=x2﹣6x+4的最小值即可.
【解答过程】解:令t=x+1,则x=t﹣1.
所以f(t)=(t﹣1)2﹣(t﹣1)+2
=t2﹣3t+4,
所以f(x)=x2﹣3x+4,
因为f(x)>3x+m对于x∈[﹣1,3]恒成立,
所以m<x2﹣6x+4对x∈[﹣1,3]恒成立,
设g(x)=x2﹣6x+4,对g(x)配方得,
g(x)=(x﹣3)2﹣5,当x=3时,g(x)有最小值﹣5,
所以m<﹣5,
故选:A. 函数
y=x
y=x2
y=x3
y= SKIPIF 1 < 0
y=x-1
图象
性质
定义域
R
R
R
{x|x≥0}
{x|x≠0}
值域
R
{y|y≥0}
R
{y|y≥0}
{y|y≠0}
奇偶性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调性
在R上单调递增
在(-∞,0]上单调递减;在(0,+∞)上单调递增
在R上单调递增
在[0,+∞)上单调递增
在(-∞,0)和(0,+∞)上单调递减
公共点
(1,1)
解析式
f (x)=ax2+bx+c(a>0)
f (x)=ax2+bx+c(a<0)
图象
定义域
R
R
值域
单调性
在x∈上单调递减;在x∈上单调递增
在x∈上单调递增;在x∈上单调递减
对称性
函数的图象关于直线x=-eq \f(b,2a)对称
新高考数学一轮复习(举一反三)重难点题型精练专题2.18 函数与方程(2份打包,原卷版+解析版): 这是一份新高考数学一轮复习(举一反三)重难点题型精练专题2.18 函数与方程(2份打包,原卷版+解析版),文件包含新高考数学一轮复习举一反三重难点题型精练专题218函数与方程原卷版doc、新高考数学一轮复习举一反三重难点题型精练专题218函数与方程解析版doc等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
新高考数学一轮复习(举一反三)重难点题型精练专题2.17 函数与方程(2份打包,原卷版+解析版): 这是一份新高考数学一轮复习(举一反三)重难点题型精练专题2.17 函数与方程(2份打包,原卷版+解析版),文件包含新高考数学一轮复习举一反三重难点题型精练专题217函数与方程原卷版doc、新高考数学一轮复习举一反三重难点题型精练专题217函数与方程解析版doc等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
新高考数学一轮复习(举一反三)重难点题型精练专题2.16 函数的图象(2份打包,原卷版+解析版): 这是一份新高考数学一轮复习(举一反三)重难点题型精练专题2.16 函数的图象(2份打包,原卷版+解析版),文件包含新高考数学一轮复习举一反三重难点题型精练专题216函数的图象原卷版doc、新高考数学一轮复习举一反三重难点题型精练专题216函数的图象解析版doc等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。












