初中数学北师大版（2024）九年级上册4 探索三角形相似的条件精品课后作业题

这是一份初中数学北师大版（2024）九年级上册4 探索三角形相似的条件精品课后作业题，文件包含专题13探索三角形相似的条件5个知识点4种题型1种中考考法原卷版docx、专题13探索三角形相似的条件5个知识点4种题型1种中考考法解析版docx等2份试卷配套教学资源，其中试卷共64页， 欢迎下载使用。

倍速学习四种方法
【方法一】 脉络梳理法
知识点1.相似三角形的概念（重点）
知识点2.相似三角形的判定方法1（重点）
知识点3.相似三角形的判定方法2（重点）（难点）
知识点4.相似三角形的判定方法3（重点）
知识点5.黄金分割的有关概念
【方法二】 实例探索法
题型1.相似三角形的判定
题型2.相似三角形判定与性质的综合应用
题型3.通过判定三角形相似得到比例式
题型4.通过判定三角形相似说明黄金分割点
【方法三】 仿真实战法
考法. 相似三角形的判定
【方法四】 成果评定法
【学习目标】
了解相似三角形的概念。
熟练掌握三角形相似的判定方法，并能灵活运用判定定理判断两个三角形是否相似。
能综合运用相似三角形的判定定理解决简单的问题。
了解黄金分割的概念及黄金比，能作出线段的黄金分割点，并会求满足黄金分割的线段的长，体会黄金分割的美。
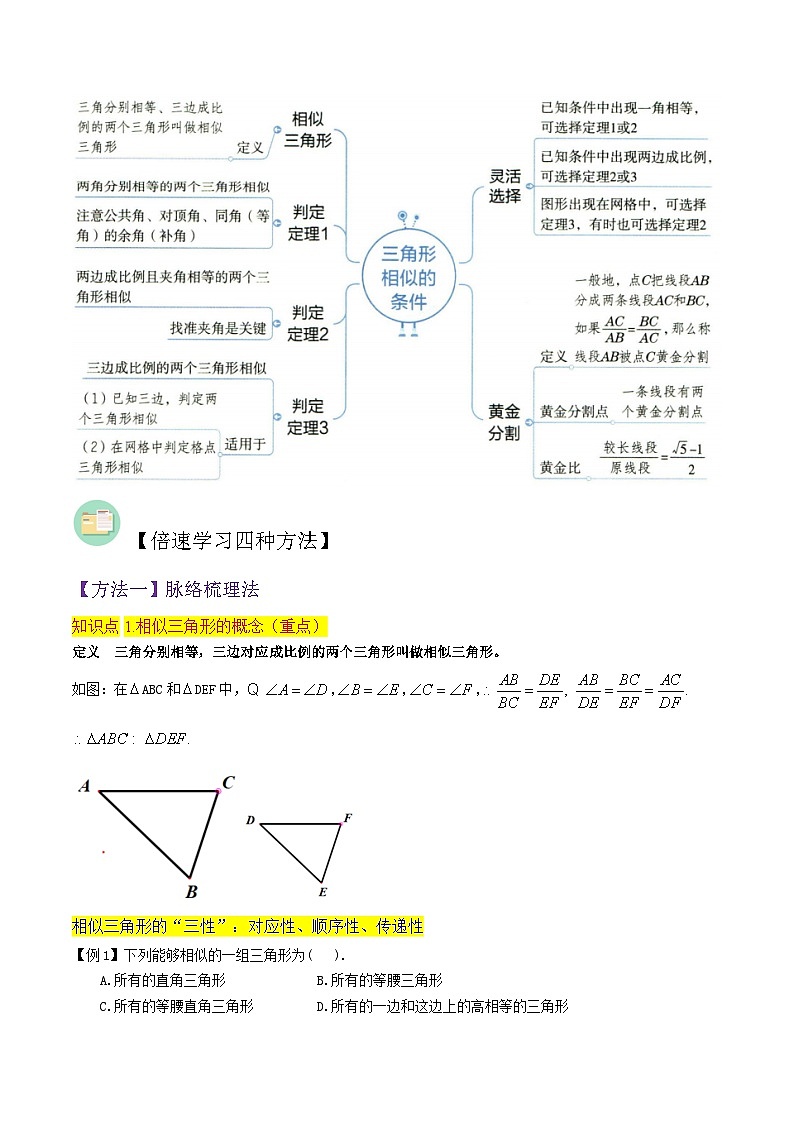
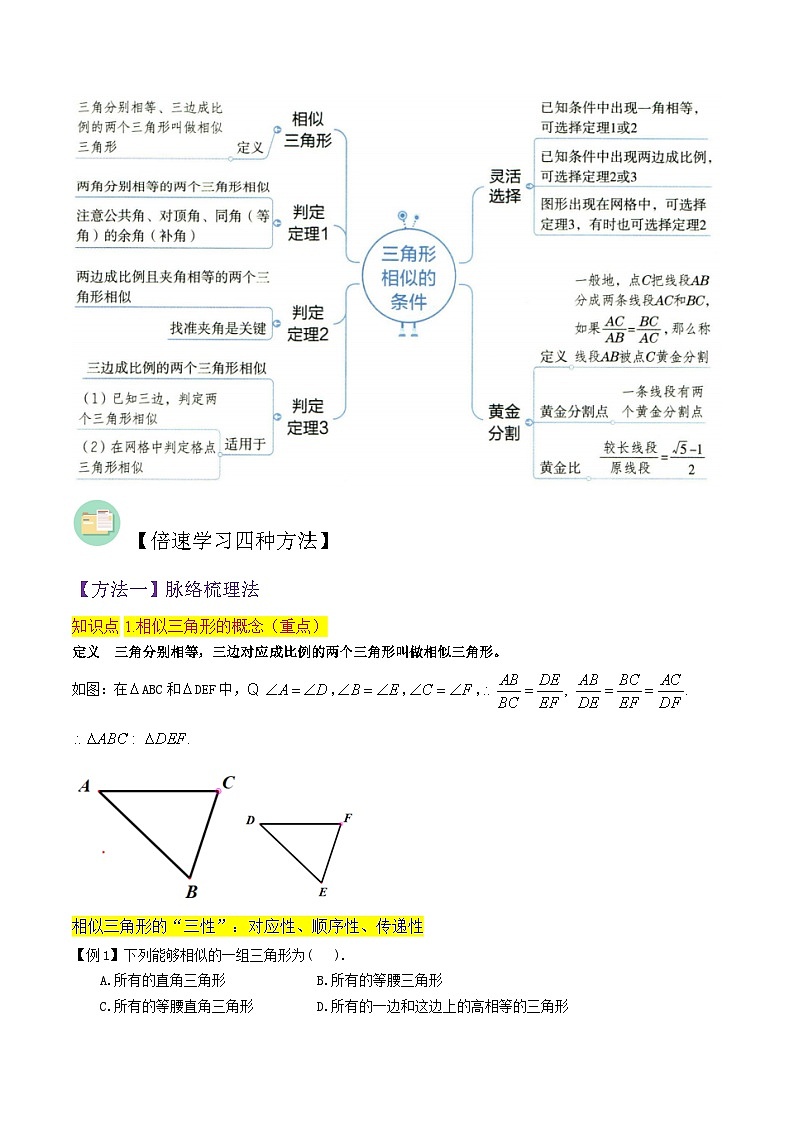
【知识导图】
【倍速学习四种方法】
【方法一】脉络梳理法
知识点1.相似三角形的概念（重点）
定义 三角分别相等，三边对应成比例的两个三角形叫做相似三角形。
如图：在ABC和DEF中，
相似三角形的“三性”：对应性、顺序性、传递性
【例1】下列能够相似的一组三角形为( ).
A.所有的直角三角形 B.所有的等腰三角形
C.所有的等腰直角三角形 D.所有的一边和这边上的高相等的三角形
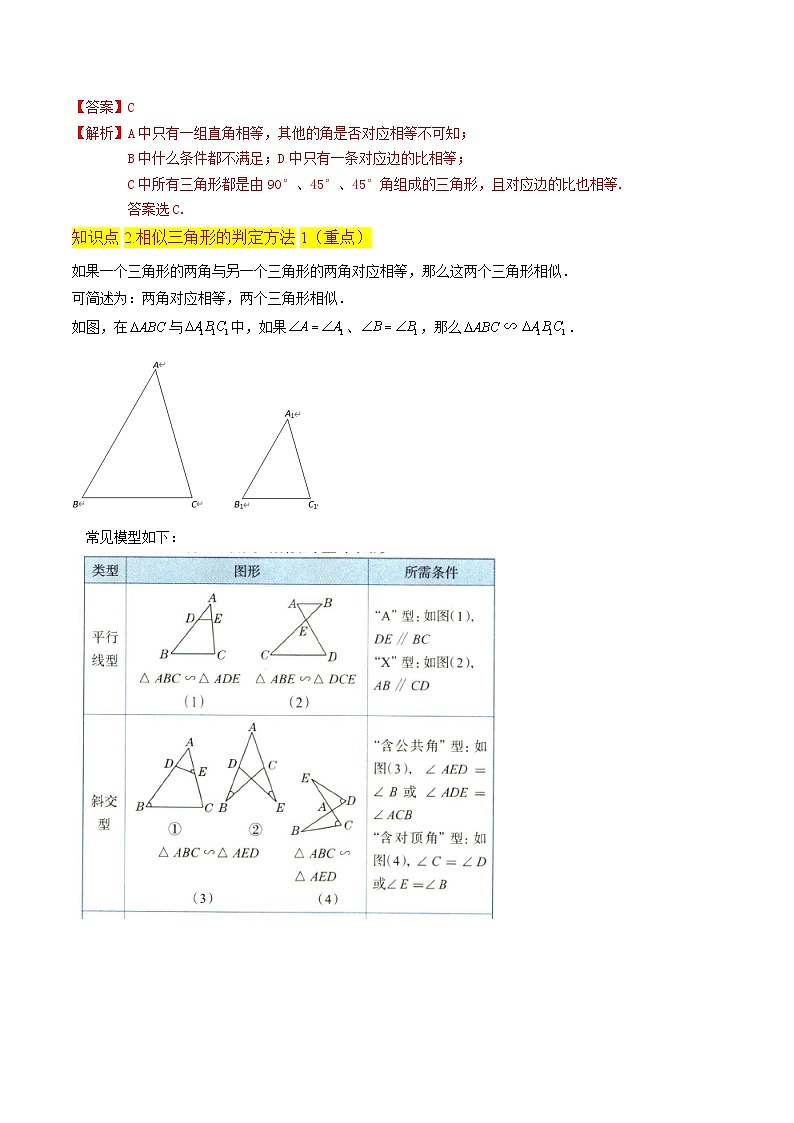
【答案】C
【解析】A中只有一组直角相等，其他的角是否对应相等不可知；
B中什么条件都不满足；D中只有一条对应边的比相等；
C中所有三角形都是由90°、45°、45°角组成的三角形，且对应边的比也相等.
答案选C.
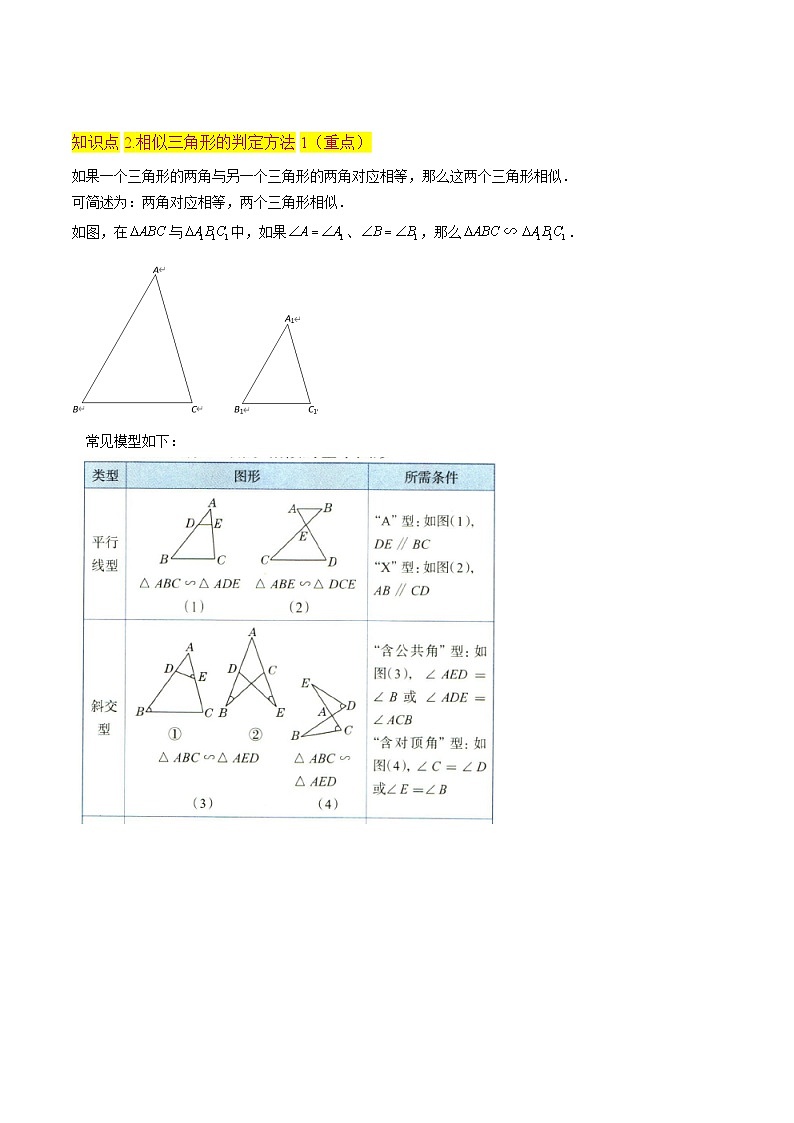
知识点2.相似三角形的判定方法1（重点）
如果一个三角形的两角与另一个三角形的两角对应相等，那么这两个三角形相似．
可简述为：两角对应相等，两个三角形相似．
如图，在与中，如果、，那么．
常见模型如下：
【例2】如图，与中， ，；证明：．

【分析】根据，得出，进而可得出结论．
解：∵，
∴，
∴，
∵，
∴．
【点拨】本题考查相似三角形的判定，掌握相似三角形的判定定理是解题的关键．
知识点3.相似三角形的判定方法2（重点）（难点）
如果一个三角形的两边与另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似．
可简述为：两边对应成比例且夹角相等，两个三角形相似．
如图，在与中，，，那么．
A
B
C
A1
B1
C1
【例3】已知如图，D，E分别是的边上的点，．
求证：．
【分析】根据“两条边对应成比例，且夹角相等的两三角形相似”即可求证．
解：∵，
又∵，
∴．
【点拨】本题考查相似三角形的判定．熟记相关判定定理是解题的关键．
知识点4.相似三角形的判定方法3（重点）
如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似．
可简述为：三边对应成比例，两个三角形相似．
如图，在与中，如果，那么∽．
A
B
C
A1
B1
C1
【例4】如图判断方格中的两个三角形是否相似，并说明理由．
【分析】根据相似三角形的判定定理判断即可．
解：相似，理由如下：
∵在中，，，，
在中，，，，
∵，，，
∴，
∴．
【点拨】本题考查了相似三角形的判定，熟知其判定定理是解题的关键．
知识点5.黄金分割的有关概念
黄金分割：一般地，点C把线段AB分成两条线段AC和BC（如图），如果，则称线段AB被点C黄金分割，点C叫线段AB的黄金分割点，其中，，AC与AB的比叫做黄金比．（注意：对于线段AB而言，黄金分割点有两个．）
【例5】已知线段的长度为，点P在线段上，，求线段的长．
【答案】．
【解析】根据题意，即有，解得，点是黄金分割点．
【总结】考查黄金分割点的定义．
【变式1】（1）点是线段的黄金分割点，，厘米，求的长；
（2）已知点是线段的黄金分割点，，求的值．
【答案】（1）；（2）或．
【解析】（1）根据黄金分割点定义，且，可知，此时
；
线段的黄金分割点有两个，与原线段比例分别为和，
故或．
【总结】注意黄金分割点和黄金分割的区别，一条线段的黄金分割点有两个，满足黄金分割黄金比的只有一个．
【变式2】如图，以长为的线段为边作正方形，取的中点，连接．
在的延长线上取点，使．以为边作正方形，点在上．
（1）求线段、的长；
（2）求证：；
（3）请指出图中的黄金分割点．
【解析】（1）是的中点，，可知，根据勾股定理得：，则，，；
证明：，即证；
根据定义可知是线段的黄金分割点，类似的，我们可以得到，
可知是线段的黄金分割点．
【总结】考查黄金比的综合应用，黄金分割题目中容易出现别的黄金分割．
【方法二】实例探索法
题型1.相似三角形的判定
1．（2023秋·全国·九年级专题练习）已知如图，D，E分别是的边上的点，．求证：．
【分析】根据“两条边对应成比例，且夹角相等的两三角形相似”即可求证．
【详解】证明：∵，
又∵，
∴．
【点睛】本题考查相似三角形的判定．熟记相关判定定理是解题的关键．
2．如图，四边形的对角线与相交于点，，，，．求证：与是相似三角形．

【分析】对应边成比例且夹角相等的两个三角形是相似三角形，由此证明即可．
【详解】证明：，，，，
，
．
，
与是相似三角形．
【点睛】本题考查相似三角形的判定，解题的关键是掌握相似三角形判定定理：对应边成比例且夹角相等的两个三角形是相似三角形．
3．（2023秋·全国·九年级专题练习）如图，点，分别在的边，上，且，，，，求证：．

【分析】根据已知线段长证，结合，两边对应成比例，夹角相等的两个三角形相似，可证．
【详解】证明：，，，，
，，
，，
，
，
（两边对应成比例，夹角相等的两个三角形相似）
【点睛】本题考查了相似三角形的判定，掌握相似三角形的判定方法是解题的关键．
4．（2023春·湖南衡阳·九年级校考阶段练习）如图，点A、B、E、D在同一条直线上，，，求证：．

【分析】根据，，得到，即可得证．
【详解】证明：∵点A、B、E、D在同一条直线上，，，
∴，
∴．
【点睛】本题考查相似三角形的判定．熟练掌握相似三角形的判定方法，是解题的关键．
5．（2023春·吉林长春·九年级统考开学考试）如图，点是的边上的一点，点为上的一点，若，，求证：．

【分析】先根据等边对等角得到，进而得到，再由即可证明．
【详解】证明：，
，

，
，
．
【点睛】本题主要考查了相似三角形的性质与判定，等边对等角，熟知两组角对应相等的两个三角形相似是解题的关键．
6．（2023秋·全国·九年级专题练习）如图，在正方形中，E是的中点，点F在上，且．

(1)求证：；
(2)与相似吗？为什么？
【分析】（1）由正方形的性质可得,，再根据可得，进而说明，再结合，即可证明结论；
（2）设，利用E为边的中点，，得到，则可计算出,由勾股定理逆定理可得以及再说明即可证明结论．
【详解】（1）解：∵正方形，
∴,
∵，
∴，
∵点F在上，
∴,
∴,
∵,
∴．
（2）解：与相似，理由如下：
设，
∵E为边的中点，，
∴，
∴，,,
∴,即,
∴,
∵,
∴,
∴．
【点睛】本题主要考查了相似三角形的判定、正方形的性质、勾股定理逆定理等知识点，掌握两组对应边的比相等且夹角对应相等的两个三角形相似是解答本题的关键．
7．（2023秋·辽宁沈阳·九年级沈阳市第一二六中学校考阶段练习）如图，，且，求证：．

【分析】由已知条件得到：，．则由“两边及夹角法”证得结论．
【详解】证明： ，
．
又，
，即，
∴．
【点睛】本题考查了相似三角形的判定．熟练掌握相似三角形的判定定理是解题的关键．
8.如图，点D为内一点，点E为外一点，且满足．求证：∽．
A
B
C
D
E
【解析】 ．
， 即．
． ∽．
【总结】本题考查相似三角形的判定定理3和相似三角形的性质知识．
题型2.相似三角形判定与性质的综合应用
9.如图，已知，下列条件中不能判断和相似的是（ ）
A．B．平分
C．D．
【答案】D
【分析】根据相似三角形的判定定理，结合平行线的性质可判断A；结合角平分线的定义可判断B；结合直角三角形两个锐角互余可判断C；D选项没有条件可判断和相似．
解：∵，
∴，
∵，
∴，故A能判断，不符合题意；
∵平分，
∴．
∵，
∴，故B能判断，不符合题意；
∵
∴，
∴．
∵，
∴．
∵，故C能判断，不符合题意；
∵，结合题意没有满足使和相似的条件，
∴不能判断，符合题意．
故选D．
【点拨】本题主要考查三角形相似的判定．掌握三角形相似的判定定理是解题关键．
10.如图，矩形的两条对角线相交于点O，，垂足为E，F是的中点，连接交于点P，那么 ．

【答案】
【分析】根据矩形性质得到，利用三角形的三线合一得，过O作交 于点Q，则有，，计算即可．
解：∵是矩形，
∴，
∵F是的中点，
∴，
又∵，
∴，
过O作交于点Q，

∴，，
∴，
故答案为：．
【点拨】本题考查矩形的性质，相似三角形的判定和性质，等腰三角形的性质，作辅助线构造三角形相似是解题的关键．
11.已知：如图，在中，，，，点D 在BC边上，且．
（1）求AD的长；
（2）取AD、AB的中点E、F，联结CE、CF、EF．求证：∽．
A
B
C
D
E
F
【解析】（1），，

．
．
在中，．
（2）点分别是AD、AB的中点，
．
在、中，，．
，
∽．
【总结】本题考查相似三角形的判定定理3、直角三角形的性质和三角形中位线等知识．
12.如图，在中，为上一点，且满足．
（1）求证：；
（2）当时，，，求的长．

【分析】（1）由三角形外角的性质和角的和差可得，再结合可得，然后结合运用两组对应角相等的三角形是相似三角形即可证明结论；
（2）先根据直角三角形的性质可得，再根据平行线的性质、等量代换可得，即是的角平分线、，进而说明，最后根据角平分线的判定定理即可解答．
（1）解：∵，，
∴，
∵，
∴．
（2）解：作 于 H．

∵，，
∴，
∵，
∴ ，
∵
∴，即是的角平分线，
∴，
∵
∴,
∵是的角平分线，，，
∴．
【点拨】本题主要考查了相似三角形的判定、三角形外角的性质、平行线的性质、角平分线的判定定理、30度所对的直角边等于斜边的一半等知识点，灵活运用相关判定、性质定理是解答本题的关键．
题型3.通过判定三角形相似得到比例式
13.如图，在中，，于D，E为AC上一点，于F，联结DF．
求证：．
A
B
C
D
E
F
【解析】证明：，， ．
又， ．
，即． 同理，得：．
， ．
又， ． ．
【总结】本题考查了三角形相似的判定方法、相似三角形的性质等知识．
题型4.通过判定三角形相似说明黄金分割点
14．（2023·山西运城·校联考模拟预测）“黄金三角形”是几何历史上的瑰宝，它有两种类型，其中一种是顶角为的等腰三角形，如图，在中，，．

(1)实践与操作：利用尺规作的平分线，交边于点（要求：尺规作图并保留作图痕迹，不写作法，标明字母）；
(2)猜想与证明：请你利用所学知识，证明点是边的黄金分割点．
【分析】（1）作的角平分线，交于点；
（2）根据等腰三角形的性质和角平分线的定义可知，再证，根据相似三角形的性质即可得证．
【详解】（1）解：如图所示，即为所求；

（2）∵在中，，，
∴，
平分，
∴，
，，
，
，
∵，，
∴，
：：，
：：，
∴，
点是边的黄金分割点．
【点睛】本题考查了黄金分割，等腰三角形、相似三角形的判定和性质，以及尺规作图等知识；熟练掌握相似三角形的性质和判定是解题的关键．
【方法三】 仿真实战法
考法. 相似三角形的判定
1．（2021•湘潭）如图，在△ABC中，点D，E分别为边AB，AC上的点，试添加一个条件： ，使得△ADE与△ABC相似．（任意写出一个满足条件的即可）
【分析】根据相似三角形判定定理：两个角相等的三角形相似；夹角相等，对应边成比例的两个三角形相似，即可解题．
【解答】解：添加∠ADE＝∠C，
又∵∠A＝∠A，
∴△ADE∽△ACB，
故答案为：∠ADE＝∠C（答案不唯一）．
【点评】本题考查了相似三角形的判定，掌握相似三角形的判定定理是解答本题的关键．
2．（2022•邵阳）如图，在△ABC中，点D在AB边上，点E在AC边上，请添加一个条件 ，使△ADE∽△ABC．
【分析】要使两三角形相似，已知一组角相等，则再添加一组角或公共角的两边对应成比例即可．
【解答】解：∵∠A＝∠A，
∴当∠ADE＝∠B或∠AED＝∠C或＝时，△ADE∽△ABC，
故答案为：∠ADE＝∠B或∠AED＝∠C或＝（答案不唯一）．
【点评】此题考查了相似三角形的判定的理解及运用，熟练应用相似三角形的判定是解题关键．
3．（2023•大庆）在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．有一张矩形纸片ABCD如图所示，点N在边AD上，现将矩形折叠，折痕为BN，点A对应的点记为点M，若点M恰好落在边DC上，则图中与△NDM一定相似的三角形是 ．
【分析】利用矩形的性质得到∠D＝∠C＝90°，然后利用折叠的性质推导出∠BMN＝∠A＝90°，进而得到∠DNM＝∠CMB，由此推断出△NDM∽△MCB．
【解答】解：∵四边形ABCD是矩形，
∴∠A＝∠D＝∠C＝90°，
∴∠DNM+∠DMN＝90°，由折叠的性质可知，∠BMN＝∠A＝90°，
∴∠DMN+∠CBM＝90°，
∴∠DNM＝∠CMB，
∴△NDM∽△MCB，
故答案为：△MCB．
【点评】本题主要考查了相似三角形的判定、矩形的性质以及翻折变换（折叠问题），熟练掌握相似三角形的判定方法是解答本题的关键：两角法：有两组角对应相等的两个三角形相似．
4．（2022•菏泽）如图，在Rt△ABC中，∠ABC＝90°，E是边AC上一点，且BE＝BC，过点A作BE的垂线，交BE的延长线于点D，求证：△ADE∽△ABC．
【分析】根据等腰三角形的性质可得∠C＝∠CEB＝∠AED，由AD⊥BE可得∠D＝∠ABC＝90°，即可得△ADE∽△ABC．
【解答】证明：∵BE＝BC，
∴∠C＝∠CEB，
∵∠CEB＝∠AED，
∴∠C＝∠AED，
∵AD⊥BE，
∴∠D＝∠ABC＝90°，
∴△ADE∽△ABC．
【点评】本题考查了相似三角形的判定，熟练掌握相似三角形的判定方法是解决问题的关键．
【方法四】 成果评定法
一、选择题
1．（2023秋·安徽蚌埠·九年级统考期末）如图，点在的边上，添加一个条件可判断，下列不满足的条件是（ ）

A．B．
C．D．
【答案】C
【分析】根据相似三角形的判定方法，逐项判断即可．
【详解】解：∵在和中，，
∴当时，满足两组角对应相等，可判断，故A不符合题意．
当时，满足两组角对应相等，可判断，故B不符合题意．
当时，其夹角不相等，则不能判断，故C符合题意．
当时，满足两边对应成比例且夹角相等，可判断，故D不符合题意．
故选：C．
【点睛】本题主要考查相似三角形的判定，掌握相似三角形的判定方法是解题的关键，即在两个三角形中，满足三边对应成比例、两边对应成比例且夹角相等或两组角对应相等，则这两个三角形相似．
2．（2023秋·浙江·九年级专题练习）下列两个三角形不一定相似的是（ ）
A．两个等边三角形B．两个顶角是的等腰三角形
C．两个全等三角形D．两个直角三角形
【答案】D
【分析】根据相似三角形的判定定理依次判断．
【详解】解：A、两个等边三角形，所有的角都是，相等，可以判定两三角形相似，故本选项错误；
B、两个顶角是的等腰三角形，两个底角一定都是，可以判定两三角形相似，故本选项错误；
C、全等是相似的特殊情况，两个全等三角形一定相似，故本选项错误；
D、两个直角三角形，只有一个直角对应相等，无法判定相似，故本选项正确．
故选：D．
【点睛】此题考查了相似三角形的判定，熟练掌握等边三角形的性质，等腰三角形的性质，全等三角形的性质及直角三角形的性质是解题的关键．
3．（2023春·吉林长春·九年级统考开学考试）如图，在中，，将沿图中的线剪开，下列四种剪开的方法中，剪下的阴影三角形与原三角形相似的是（ ）

A．①②B．③④C．①③D．①③④
【答案】C
【分析】根据相似三角形的判定定理对各选项进行逐一判定即可．
【详解】①阴影部分的三角形与原三角形有两个角对应相等，故两三角形相似；
②阴影部分的三角形与原三角形仅有一个角对应相等，故两三角形不一定相似；
③两三角形对应边不仅满足，且夹角相等，故两三角形相似；
④两三角形对应边虽然满足，但夹角不一定相等相等，故两三角形不一定相似；
故正确的有：①③，
故选：C．
【点睛】本题考查的是相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键．
4．（2023秋·全国·九年级专题练习）含角的直角三角板与含角的直角三角板如图放置，它们的斜边与斜边相交于点E．下列结论正确的是（ ）
A．B．
C．D．
【答案】A
【分析】根据相似三角形的判定方法，进行判断即可．
【详解】解：由图可知：，
∴，
∴，
∴；
故选A．
【点睛】本题考查相似三角形的判定．熟练掌握相似三角形的判定方法，是解题的关键．
5．（2023秋·九年级课时练习）如图，根据图中给出的数据，一定能得到（ ）
A． B． C． D．
【答案】C
【分析】先根据题意，推出，再根据相似三角形的判定条件即可得到答案．
【详解】解：， ，，，
，，
，，
，
，
，
故选：C．
【点睛】本题考查了相似三角形的判定，熟练掌握相似三角形的判定条件是解题关键．
6．（2023秋·浙江·九年级专题练习）如图，每个小正方形的边长均为，则下列图形中的三角形（阴影部分）与相似的是（ ）
A．B．
C．D．
【答案】B
【分析】根据题意可得：，，，然后根据三组对应边的比相等的两个三角形相似可对各选项进行判定即可．
【详解】解：∵每个小正方形的边长均为，
∴，，，
A．该三角形的三边分别为：，，，但，则这个三角形与不相似，故此选项不符合题意；
B．该三角形的三边分别为：，，，且，则这个三角形与相似，故此选项符合题意；
C．该三角形的三边分别为：，，，但，则这个三角形与不相似，故此选项不符合题意；
D．该三角形的三边分别为：，，，但，则这个三角形与不相似，故此选项不符合题意．
故选：B．
【点睛】本题考查相似三角形的判定，正方形的性质，勾股定理，注意：三组对应边的比相等的两个三角形相似．掌握相似三角形的判定是解题的关键．
7．（2023秋·全国·九年级专题练习）如图，每个小正方形边长均为1，则图中的三角形中与相似的是（ ）

A．B．C．D．
【答案】B
【分析】直接利用相似三角形的判定方法结合正方形的性质分析得出答案．
【详解】解：由题意可得：，，
，，，，
，，
，
又，
．
故选：B．
【点睛】此题主要考查了相似三角形的判定，正确得出对应边的关系是解题关键．
8.（2023春·山东烟台·九年级统考期末）我们把宽与长的比等于5−12的矩形称为黄金矩形．如图，在黄金矩形ABCD（ABA．22B．5−12C．3−52D．5+12
【答案】B
【分析】设BC=a，根据黄金矩形的概念求出AB，结合图形计算，得到答案．
【详解】解：设BC=a，
∵矩形ABCD为黄金矩形，
∴AB=5−12a，
∴BE=a-5−12a=3−52a，
∴⋅BEAB=(3−5)a2(5−1)a2=5−12，
故选：B．
【点睛】本题考查的是黄金分割、矩形的性质，掌握黄金比值为5−12是解题的关键．
9.（2023春·辽宁丹东·九年级统考期末）如图，点C是线段AB的黄金分割点，且ACA．BCAB≈0.618B．BC=3−52AC
C．BC2=AB⋅ACD．ACBC=5−12
【答案】B
【分析】根据黄金分割的定义得BCAB=ACBC=5−12≈0.618，即可解决问题．
【详解】解：∵点C是线段AB的黄金分割点，且AC∴BCAB=ACBC=5−12≈0.618，
∴BC2=AB⋅AC，AC=5−12BC，
∴A、C、D选项不符合题意，
故选：B．
【点睛】本题考查了黄金分割，解题的关键是掌握黄金分割的定义：把一条线段分割为两部分，使较大部分与全长的比值等于较小部分与较大的比值，这个比值为5−12，近似值为0.618，即为黄金分割．
10．（2023秋·全国·九年级专题练习）已知是中的边上的一点，，的平分线交边于，交于，那么下列三角形中与一定相似的是（ ）

A．B．C．D．
【答案】C
【分析】利用角平分线的性质结合相似三角形的判定方法得出,进而得出，即可得出．
【详解】∵平分，
∴，
∵，
∴，
∴，
∴，
∵，
∴，
故选: ．
【点睛】此题考查了相似三角形的判定，解题的关键是要识别两三角形相似，掌握定义外，还要注意正确找出两三角形的对应边和对应角．
二、填空题
11．（2023秋·全国·九年级专题练习）如图，已知，请再添加一个条件，使，你添加的条件是 （写出一个即可）．
【答案】或
【分析】根据相似三角形的判定定理即可进行解答．
【详解】解：添加，
∵，
∴；
添加，
∵，，
∴；
故答案为：或．
【点睛】本题主要考查了相似三角形的判定定理，解题的关键是掌握：三边分别成比例的两个三角形相似；两边成比例，夹角相等的两个三角形相似；有两个角相等的两个三角形相似．
12．（2023秋·河南漯河·九年级统考期末）如图，在中，，，点为中点，点在上，当为 时，与以点A、D、E为顶点的三角形相似．

【答案】3或
【分析】先得到，再分与两种情况讨论即可解答．
【详解】解：当时，
∵，
∴，
∴，
当时，
∵，
∴，
∴，
综上，或，
故答案为：3或．
【点睛】本题考查了相似三角形的判定，解题的关键是分类讨论思想的运用及熟练掌握相似三角形的判定定理．
13．（2023秋·九年级课时练习）如图，的高，相交于点，写出一个与相似的三角形，这个三角形可以是 ．
【答案】（答案不唯一）
【分析】根据已知条件得，，推出，其他同理.
【详解】解： ；
证明：∵的高，相交于点，
∴，
∵，
∴；
故答案为：（答案不唯一）.
【点睛】本题考查相似三角形的判定，三角形的高的定义，解题的关键是掌握有两角对应的两个三角形相似.
14．（2023·全国·九年级专题练习）在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．有一张矩形纸片如图所示，点在边上，现将矩形折叠，折痕为，点对应的点记为点，若点恰好落在边上，则图中与一定相似的三角形是 ．

【答案】
【分析】由矩形的性质得，从而得到，由折叠的性质可得：，从而得到，由此推断出．
【详解】解：四边形是矩形，
，
，
由折叠的性质可得：，
，
，
，
，
故答案为：．
【点睛】本题主要考查了矩形的性质、折叠的性质、相似三角形的判定，熟练掌握矩形的性质、折叠的性质、相似三角形的判定，是解题的关键．
15.（2023春·江苏南京·九年级统考期末）已知线段AB=2，若C，D是AB的两个黄金分割点，则CD长为 ．
【答案】25−4
【分析】根据黄金分割的概念先计算出AC，然后再计算AD，最后根据CD=AC−AD即可求出答案．
【详解】如图，C，D是AB的两个黄金分割点，设AC>BC，AD根据题意得，AC=BD=5−12AB=5−12×2=5−1
∴ AD=AB−BD=2−5−1=3−5
∴ CD=AC−AD=5−1−3−5=25−4．
故答案为:25−4．
【点睛】本题考查了黄金分割的概念：把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值5−12叫做黄金比，熟练掌握黄金比是解题的关键．
16.（2023春·全国·九年级统考期中）人体下半身与身高的比例越接近0.618，越给人美感．遗憾的是，即使芭蕾舞演员也达不到如此的完美．某女士身高1.68m，下半身1.02m，她应该选择穿 （精确到0.1cm）的高跟鞋看起来更美．
【答案】4.8
【分析】设她应选择高跟鞋的高度是xcm，根据黄金分割的定义，列出方程直接求解即可．
【详解】设她应选择高跟鞋的高度是xcm，则
102+x168+x=0.618，
解得：x≈4.8cm．
经检验知x≈4.8是原方程的解，
答：她应该选择穿4.8cm的高跟鞋看起来更美．
故答案为4.8．
【点睛】此题主要考查了黄金分割，据题黄金分割的定义列出方程是本题的关键．注意身高不要忘记加上高跟鞋的高度．
17.（2023春·四川成都·九年级统考期末）如图，线段AB=1，点C是线段AB的黄金分割点AC>BC，C1是线段AC的黄金分割点C1AC1>C1C，C2是线段AC1的黄金分割点，以此类推，则ACm= ．
【答案】5−12m+1
【分析】先按照黄金分割比例依次计算出AC、AC1、AC2，然后按照规律即可得到ACm．
【详解】解：设AC=a，BC=BA−AC=1−a，
∵点C是线段AB的黄金分割点AC>BC，
∴ BCAC=ACAB，
即1−aa=a1，整理得a2+a−1=0，
解得a=5−12或a=−5−12（舍去），
∴ACAB=5−12，AC=5−12，
∵ C1是线段AC的黄金分割点C1AC1>C1C，
∴ AC1AC=5−12，AC1=5−122，
∵ C2是线段AC1的黄金分割点，
∴ AC2AC1=5−12，AC2=5−123，
∵ AC=5−12、AC1=5−122、AC2=5−123，
∴以此类推，ACm=5−12m+1，
故答案为：5−12m+1．
【点睛】本题考查了黄金分割、规律探究表达，求出黄金分割比，并按照规律表示出ACm是解题关键．
18.（2023春·甘肃白银·九年级校考期末）节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体．若舞台AB长为20m，则主持人站在离A点 处最自然得体．（结果精确到0.1m）
【答案】12.4m或7.6m
【分析】根据黄金分割定义，由黄金分割点的位置分两种情况讨论：①黄金分割点离A近；②黄金分割点离B近，由黄金分割比列式求解即可得到答案．
【详解】解：由题意可知，分两种情况，作图求解：
当①黄金分割点离A近，如图所示：
∵ AB=20m，
∴由黄金分割比可知ACBC=BCAB，
设AC=xm，则BC=20−xm，代入得到x20−x=20−x20，解得x=30±105，
∴AC=30−105≈7.6m，AC=30+105>20（舍弃）；
②黄金分割点离B近，如图所示：
∵ AB=20m，
∴由黄金分割比可知BCAC=ACAB，
设AC=ym，则BC=20−ym，代入得到20−yy=y20，解得x=−10±105，
∴AC=−10+105≈12.4m，AC=−10−105<0（舍弃）；
综上所述，主持人站在离A点12.4m或7.6m处最自然得体，
故答案为：12.4m或7.6m．
【点睛】本题考查利用黄金分割解决实际问题，读懂题意，熟练掌握黄金分割比与黄金分割点是解决问题的关键．
三、解答题
19．（2023秋·浙江·九年级专题练习）如图，在平行四边形中，点E为边上的点（不与点B，点C重合），连接并延长，交的延长线于点F．求证：．

【分析】根据平行四边形的性质和平行线的性质证明，，即可证得结论．
【详解】证明：∵四边形是平行四边形，
∴，，
∴，
∴．
【点睛】本题考查了平行四边形的性质和平行线的性质以及相似三角形的判定，熟练掌握上述知识是解题的关键．
10．（2023·上海·九年级假期作业）如图，，那么图中相似的三角形有哪几对？

【答案】，，，．
【分析】根据有两组角对应相等的两个三角形相似可以判断，，，．
【详解】解：根据，同时有公共角必相等，
根据相似三角形判定定理，可得，，；
同时由，
可得：，
得：，
又，
根据相似三角形判定定理，得：．
【点睛】题目主要考查相似三角形判定定理，同时要注意根据题目条件推出一些其它角相等的条件，注意不要遗漏．
21．（2023秋·浙江·九年级专题练习）如图，、相交于点，已知，，，．求证：．
【分析】首先根据各线段的长，可证得，再根据相似三角形的判定定理，即可证得结论．
【详解】证明：∵，，，，
∴，，
∴，
又∵，
∴．
【点睛】本题考查相似三角形的判定，熟练掌握和运用相似三角形的判定定理是解题的关键．
22．（2023秋·全国·九年级专题练习）如图，与中，，；证明：．

【分析】根据，得出，进而可得出结论．
【详解】证明：∵，
∴，
∴，
∵，
∴．
【点睛】本题考查相似三角形的判定，掌握相似三角形的判定定理是解题的关键．
23．（2023·浙江杭州·校联考三模）如图所示，延长平行四边形一边至点F，连接交于点E，若．

(1)求证：；
(2)若，求的长．
【答案】(1)见解析
(2)9
【分析】（1）根据平行四边形的性质可得，则，即可求证；
（2）根据平行四边形的性质可得，根据相似三角形的性质可得，即可求解．
【详解】（1）证明：∵四边形是平行四边形，
∴，
∴，
∴；
（2）解：∵四边形是平行四边形，
∴，
由（1）可得，，
∴，
∴．
【点睛】本题主要考查了平行四边形的性质，相似三角形的判定和性质，解题的关键是掌握平行四边形对边平行且相等；相似三角形对应边成比例．
24．（2023秋·全国·九年级专题练习）如图，和的顶点都在边长为1的小正方形的顶点上

(1)求证：
(2)的的面积比为________．
【答案】(1)见解析；
(2)，见解析．
【分析】（1）根据勾股定理求得两三角形三边长，按大小边顺序，求出两三角形对应三边比，根据“两三角形三边对应成比例，两三角形相似”得证．
（2）根据相似三角形性质“面积比等于相似比的平方”求解．
【详解】（1）解：由图知，，，，，，，
∴，，；
∴
∴
（2）解：∵
∴的的面积比为，即．
【点睛】本题考查相似三角形的判定和性质，勾股定理，掌握相似三角形的判定方法及性质是解题的关键．
25．（2023秋·浙江·九年级专题练习）如图，在中，，是边上的高．
(1)求证：；
(2)若，，求的长．
【答案】(1)证明见解析
(2)
【分析】（1）由已知可得，又因为，根据相似三角形的判定即可得证；
（2）根据勾股定理得到，根据三角形的面积公式得到，然后根据勾股定理即可得到结论．
【详解】（1）证明：∵是边上的高，
∴，
∵，
∴
∵，
∴；
（2）解：∵，是边上的高，，，
∴，，
∵，
∴，
∴，
∵，
∴，
∴的长为．
【点睛】本题考查相似三角形的判定，勾股定理，三角形高的定义．掌握相似三角形的判定是解题的关键．
26．（2023秋·全国·九年级专题练习）如图，在中，为上一点，且满足．

(1)求证：；
(2)当时，，，求的长．
【答案】(1)见解析
(2)
【分析】（1）由三角形外角的性质和角的和差可得，再结合可得，然后结合运用两组对应角相等的三角形是相似三角形即可证明结论；
（2）先根据直角三角形的性质可得，再根据平行线的性质、等量代换可得，即是的角平分线、，进而说明，最后根据角平分线的判定定理即可解答．
【详解】（1）解：∵，，
∴，
∵，
∴．
（2）解：作 于 H．

∵，，
∴，
∵，
∴ ，
∵
∴，即是的角平分线，
∴，
∵
∴,
∵是的角平分线，，，
∴．
【点睛】本题主要考查了相似三角形的判定、三角形外角的性质、平行线的性质、角平分线的判定定理、30度所对的直角边等于斜边的一半等知识点，灵活运用相关判定、性质定理是解答本题的关键．