四川省绵阳市三台县2024届九年级下学期中考二模数学试卷(含解析)

这是一份四川省绵阳市三台县2024届九年级下学期中考二模数学试卷(含解析)，共24页。试卷主要包含了考试结束后，将答题卡收回．， 下列运算正确的是等内容，欢迎下载使用。

注意事项：
1.答题前，考生先将自己的学校、姓名、班级、考号用0.5毫米的黑色墨迹签字笔填写清楚，再用2B铅笔将考号准确填涂在“考号”栏内．
2.选择题使用2B铅笔填涂在答题卡对应题目标号位置上，非选择题用0.5毫米黑色签字笔书写在答题卡对应框内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．
3.考试结束后，将答题卡收回．
第Ⅰ卷 选择题（36分）
一、选择题：本大题共12个小题，每小题3分，共36分，每个小题只有一个选项符合题目要求．
1. 的倒数为（ ）
A. B. C. 2024D.
【答案】D
解析：解：的倒数为，
故选D
2. 三台经济主要以纺织鞋服为主导，加上健康食品医药、新能两大产业，构成了三台的产业格局．围绕三大产业做文章，不断拓展产业集群是三台经济不断增长的关键．2023年三台经济增长快速，GDP已经达到530亿元，用科学记数法表示530亿元是（ ）
A. B. C. D.
【答案】B
解析：解：亿
故选：B．
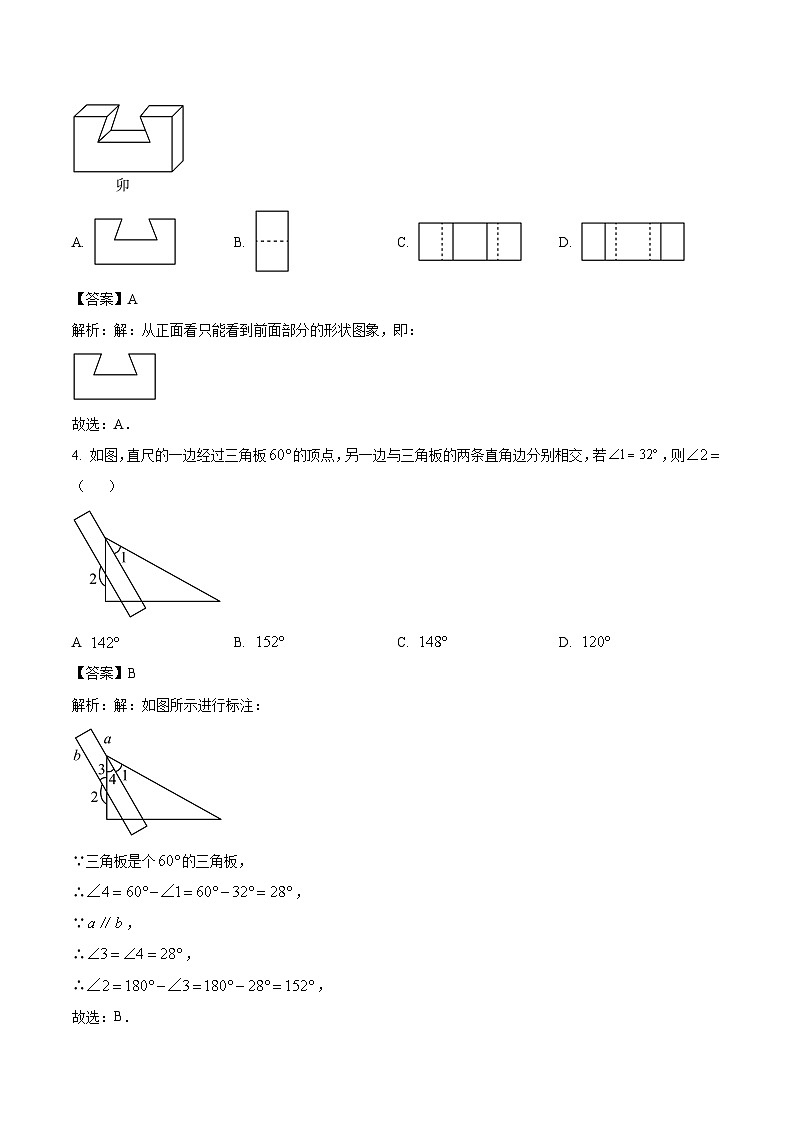
3. 我国古代建筑中经常使用榫卯构件，如图是某种卯构件的示意图，其主视图是（ ）

A. B. C. D.
【答案】A
解析：解：从正面看只能看到前面部分的形状图象，即：

故选：A．
4. 如图，直尺的一边经过三角板的顶点，另一边与三角板的两条直角边分别相交，若，则（ ）
A B. C. D.
【答案】B
解析：解：如图所示进行标注：
∵三角板是个的三角板，
∴，
∵，
∴，
∴，
故选：B．
5. 如图，在中，，在同一平面内，将绕点A逆时针旋转到的位置，使得，则等于（ ）
A. B. C. D.
【答案】D
解析：解：∵将绕点A逆时针旋转到的位置，
∴，
∴，，
∵，，
∴，
∴，
∴．
故选：D
6. 下列运算正确的是（ ）
A. B. C. D.
【答案】D
解析：解：A. ，原选项计算错误，故不符合题意；
B. ，原选项计算错误，故不符合题意；
C. ，原选项计算错误，故不符合题意；
D. ，计算正确，符合题意，
故选：D
7. 在北京举行的2022年冬季奥运会，激起了人们对冰雪运动的极大热情．如图是某滑雪场雪道缆车线路示意图，滑雪者从点A出发，途经点B时高度上升了100m，最后到达终点C．已知BC=300m，且BC段的运行路线与水平面的夹角为37°，他从点A运行到点C垂直上升的高度约是（ ）(结果保留整数．参考数据：
A. 280mB. 300mC. 325mD. 340m
【答案】A
解析：解：在Rt△BCE中，∵∠CBE=37°，BC=300，
∴sin∠CBE=，
即，
解得CE=180m，
∵EF=BD=100m，
∴CF=CE＋EF=180＋100=280m；
故选：A．
8. 如图，圆锥的底面半径为，母线的长为，则这个圆锥侧面展开图扇形的圆心角为（）度．
A. 120B. 150C. 135D. 125
【答案】A
解析：解：圆锥底面周长，
∴这个圆锥侧面展开图扇形的圆心角为圆锥底面周长．
故选:．
9. 用白铁皮做罐头盒，每张铁皮可制盒身个，或制盒底个，一个盒身与两个盒底配成一套罐头盒，现有张白铁皮，用多少张制盒身，多少张制盒底可以使盒身与盒底正好配套？设用张制盒身，张制盒底.根据题意可列出的方程组是（ ）
A. B.
C. D.
【答案】D
解析：解：设用张制盒身，张制盒底，可得方程组，
故选：D．
10. 若关于的方程解为正数，则的取值范围是（ ）
A. B. C. 且D. 且
【答案】D
解析】解：
∵方程的解为正数，且分母不等于0
∴，
∴，且
故选：D．
11. 如图，被称为“杨辉三角”或“贾宪三角”．其规律是：从第二行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和，表中两平行线之间的一列数：1，3，6，10，15，…，我们把第一个数记为，第二个数记为，第三个数记为，…，第n个数记为．则的值为（ ）
A. 100B. 199C. 5050D. 10000
【答案】C
解析：解：由题意可得：
，
，
，
，
∴，
∴当时，，
故选：C．
12. 如图，将矩形ABCD沿着GE、EC、GF翻折，使得点A、B、D恰好都落在点O处，且点G、O、C在同一条直线上，同时点E、O、F在另一条直线上．小炜同学得出以下结论：①GF∥EC；②AB=AD；③GE=DF；④OC=2OF；⑤△COF∽△CEG．其中正确是（ ）
A. ①②③B. ①③④C. ①④⑤D. ②③④
【答案】B
解析：解：根据折叠的性质知∠DGF=∠OGF，∠AGE=∠OGE，
∴∠FGE=∠OGF+∠OGE=(∠DGO+∠AGO) =90°，
同理∠GEC=90°，
∴∠FGE+∠GEC=180°
∴GF∥EC；故①正确；
根据折叠的性质知DG=GO，GA=GO，
∴DG=GO=GA，即点G为AD的中点，
同理可得点E为AB的中点，
设AD=BC=2a，AB=CD=2b，则DG=GO=GA=a，OC=BC=2a，AE=BE=OE=b，
∴GC=3a，
在Rt△CDG中，CG2=DG2+CD2，
即(3a)2=a2+(2b)2，
∴b=，
∴AB=2=AD，故②不正确；
设DF=FO=x，则FC=2b-x，
在Rt△COF中，CF2=OF2+OC2，
即(2b-x)2=x2+(2a)2，
∴x==，即DF=FO=，
GE=a，
∴，
∴GE=DF；故③正确；
∴，
∴OC=2OF；故④正确；
∵∠FCO与∠GCE不一定相等，
∴△COF∽△CEG不成立，故⑤不正确；
综上，正确的有①③④，
故选：B．
第Ⅱ卷 非选择题（共114分）
二、填空题：本大题共6个小题，每小题4分，共24分，将答案填写在答题卡相应的横线上．
13. 因式分解：＝________________．
【答案】
解析：解：
．
故答案为：．
14. 不等式组的最小整数解是__________．
【答案】0
解析：

解不等式①，得
解不等式②，得
原不等式组的解集为
原不等式组的最小整数解为0.
故答案为0.
15. 四边形与四边形位似，位似中心为点．点与点对应，若，四边形的面积为8，则四边形的面积为______．
【答案】72
解析：解：∵，
∴，
∵，
∴，
故答案为：．
16. 若关于x的分式方程有解，且关于y的方程有实数根，则的范围是______．
【答案】且
解析：解：，化简得：，
∵，即，
∴，解得：，
∵有实数根，
∴，
解得：，
∴综上且，
故答案为：且．
17. 如图，在平面直角坐标系中，为坐标原点，抛物线的对称轴为，与轴的一个交点位于，两点之间．下列结论：①；②；③；④若x1，x2为方程的两个根，则；其中正确的有______（填序号）．
【答案】③④
解析：∵抛物线的对称轴为直线，
∴，
∴，
∴，故①错误；
∵抛物线开口向下，对称轴在轴的右边，与轴交点在正半轴上，
∴，，，
∴，故②错误；
∵抛物线的对称轴为直线，时，
∴时，，即，
∴，
∴，故③正确；
∵由图象可得：，，
∴，故④正确；
∴正确的有③④，
故答案为：③④．
18. 正方形对角线、相交于点，点是边上一动点，连接交于点，过点作，垂足为，连接，当点运动到恰好使时，则的值是______．
【答案】##
解析：解：取的中点，连接、，过点作于点，
设正方形的边长为，
∵四边形是正方形，
∴，，，，
∴，
∵，，是的中点，
∴，
∴点、、、，四点共圆，
∵，
∵，
∴
∴，
∴，
∵，
∴（），
∴，
∴，
∵，，
∴，
∴，
∵，
∴，，
∴．
三、解答题：本大题共7个小题，共90分，解答应写出文字说明，证明过程或演算步骤．
19. （1）计算：；
（2）化简求值： ，其中．
【答案】（1）；（2），
解析：（1）
解：原式
（2）
解：原式
当时，
原式
20. 中考体考已经结束，为了更好地分析初三年级学生的体育水平，现从体育考试成绩中随机抽查了名男生和名女生的体考成绩进行整理、描述和分析（成绩得分用x表示，共分成四组：：，：，：，：），下面给出了部分信息：
名男生的体考成绩（单位：分）：．
名女生的体考成绩为等级的数据为：．
所抽取的学生体考成绩统计表：
根据以上信息，解答下列问题：
（1）直接写出上述图表中______，_____；
（2）若该校有名学生，请估计获得等级的学生共有多少人？
（3）体考选考项目由学生自愿选择，现有男女各一名同学准备从排球、乒乓球、羽毛球三个项目中选择自己擅长的项目，求这两名同学选择相同项目的概率．
【答案】（1），
（2）人
（3）
【小问1解析】
解：名男生的体考成绩按从低到高排列为：，排在第位和第位的数为，
∴，
在个数据中，出现的次数最多，
∴，
故答案为：，；
【小问2解析】
解：由题意可得，男生体考成绩为等级的有人，名女生体考成绩为等级的有人，
∴，
答：估计获得等级的学生共有人；
【小问3解析】
解：设排球、乒乓球、羽毛球分别用表示，
画树状图如下：
由树状图可得，共有种等结果，其中这两名同学选择相同项目的结果有种，
∴这两名同学选择相同项目的概率为．
21. 如图，一次函数的图像与反比例函数的图像交于，两点．（，，为常数）

（1）求一次函数和反比例函数的解析式；
（2）根据图像直接写出不等式的解集；
（3）为轴上一点，若的面积为，求点的坐标．
【答案】（1）；
（2）或，
（3）或．
【小问1解析】
解：将点代入得，
∴，
∴反比例函数的解析式为；
将点代入得，
∴，
将点、分别代入得，
解得，
∴一次函数的解析式为；
【小问2解析】
根据图像可知，当时，直线在反比例函数图像的上方，满足，
∴不等式的解集为或；
【小问3解析】
如图过点作轴平行线与交于点，分别过点，作直线垂线，垂足分别为点、，
设，则，
∴，
则，
，
，
，
，
∵的面积为，
∴，
∴，
即点的坐标为．

如图，过作轴于点，过作轴于点，设，

由（1）得：，，
∴，，
∴，，，
则
，
，
∴，
即点的坐标为，
综上所述：或．
22. 如图，在中， ，垂足为，，垂足为，与，分别相交于点，，．
（1）求证：四边形是菱形；
（2）若，．
①求；
②求的面积．
【答案】（1）见解析 （2）①；②
【小问1解析】
证明：∵，，
∴，
∴，，
∵四边形是平行四边形，
∴，
∴，
∵，
∴，
∴，
∴在和中
∴，
∴，
∴是菱形；
【小问2解析】
①解：∵，
∴，
∴，
∵,，
∴，
∵在菱形中，，
∴，
∵，
∴；
②∵，
∴，
∴，
∴，
∴．
23. 某超市销售、两种品牌的盐皮蛋，若购买箱种盐皮蛋和箱种盐皮蛋共需元；若购买箱种盐皮蛋和箱种盐皮蛋共需元．
（1）种盐皮蛋、种盐皮蛋每箱价格分别是多少元？
（2）若某公司购买、两种盐皮蛋共箱，且种的数量至少比种的数量多箱，又不超过种的倍，怎样购买才能使总费用最少？并求出最少费用．
【答案】（1）种盐皮蛋每箱价格为元，种盐皮蛋每箱价格为元
（2）购买箱种盐皮蛋，箱种盐皮蛋才能使总费用最少，最少费用为元
【小问1解析】
解：设种盐皮蛋每箱价格为元，种盐皮蛋每箱价格为元，
由题意可得：，
解得，
答：种盐皮蛋每箱价格为元，种盐皮蛋每箱价格为元；
【小问2解析】
解：设购买种盐皮蛋箱，则购买种盐皮蛋箱，总费用为元，
由题意可得：，
∴随的增大而增大，
∵种的数量至少比种的数量多箱，又不超过种的倍，
∴，
解得，
∵为整数，
∴当时，取得最小值，此时，，
答：购买箱种盐皮蛋，箱种盐皮蛋才能使总费用最少，最少费用为元．
24. 如图，在中， ，以斜边上的中线为直径作，与、分别交于点M、N，与的另一个交点为E．过点N作，垂足为F，连接交于H；其中，．
（1）求证：是的切线；
（2）求和的长．
【答案】（1）证明见解析
（2），
【小问1解析】
证明：连接，，如图，
在中，，为斜边中线，
∴，
∵是的直径．
∴，
∴，
∴，
∵，
∴，
∴，
∴，
∵，
∴，
∵是的半径，
∴是的切线；
【小问2解析】
解：如图所示，连接，
在中，由勾股定理得，
由（1）得点N为得中点，
∵，
∴，
∵，
∴，
∴，即，
∴；
∵D、N分别是的中点，
∴是是中位线，
∴，
∴，
∴，
∴．
25. 已知抛物线与x轴交于A，B两点，与y轴交于点，其对称轴为．

（1）求抛物线的表达式；
（2）如图1，点D是线段上的一动点，连接，将沿直线翻折，得到，当点恰好落在抛物线的对称轴上时，求点D的坐标；
（3）如图2，动点P在直线上方的抛物线上，过点P作直线的垂线，分别交直线，线段于点E，F，过点F作轴，垂足为G，求的最大值．
【答案】（1）
（2）
（3）
【小问1解析】
解：抛物线与y轴交于点，
∴，
∵对称轴为，
∴，，
∴抛物线的解析式为；
【小问2解析】
如图，过作x轴的垂线，垂足为H，

令，
解得：，
∴，，
∴，
由翻折可得，
∵对称轴，
∴，
∵，
∴，
∴，
在中，，
∴；
【小问3解析】
设所在直线的解析式为，
把B、C坐标代入得：，
解得，
∴，
∵，
∴，
∵，
∴直线与x轴所成夹角为，
设，
设所在直线的解析式为：，
把点P代入得，
∴，
令，则，
解得，
∴
∴
∵点P在直线上方，
∴，
∴当时，的最大值为．
性别
平均数
中位数
众数
男
女