




2024年高考数学新高考Ⅰ卷试卷评析及备考策略(课件)
展开解构经典试题 注重教考衔接
共享复习策略科学备战高考
2024高考试卷评析暨2025高考备考策略
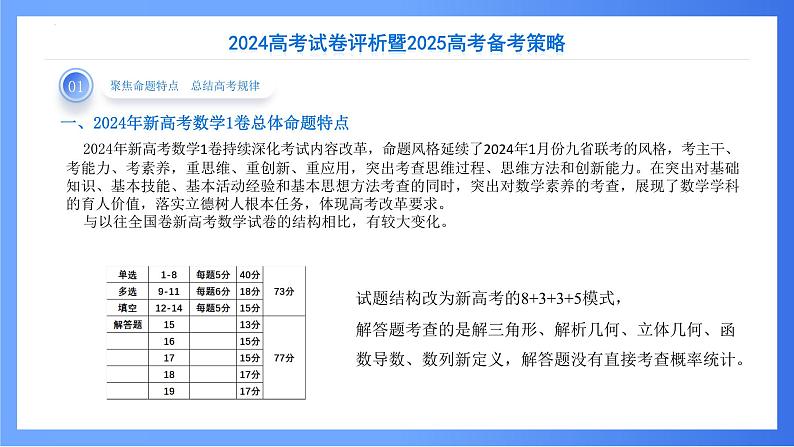
一、2024年新高考数学1卷总体命题特点
2024年新高考数学1卷持续深化考试内容改革,命题风格延续了2024年1月份九省联考的风格,考主干、考能力、考素养,重思维、重创新、重应用,突出考查思维过程、思维方法和创新能力。在突出对基础知识、基本技能、基本活动经验和基本思想方法考查的同时,突出对数学素养的考查,展现了数学学科的育人价值,落实立德树人根本任务,体现高考改革要求。与以往全国卷新高考数学试卷的结构相比,有较大变化。
试题结构改为新高考的8+3+3+5模式,解答题考查的是解三角形、解析几何、立体几何、函数导数、数列新定义,解答题没有直接考查概率统计。
试题淡化解题技巧,注重通性通法。测试卷题目的设置层次递进有序,难度结构合理,大部分为常规题目。中低难度的题目平和清新,重点突出;高难度的题目不偏不怪,中规中矩,体现了良好的区分性。第1、2、3、4、5、12、13、15、16题第1问(约55分)属于简单题,主要考查基本概念和基本运算。第6、7、9、10、13、19题第1问(约30分)属于中等偏易题,主要考查常规的计算和推理。第8、11、16题第2问、17、18题第1、2小问,第19题第2问(约40分)属于中等偏难题,主要考查逻辑推理能力、数学运算能力、化归转化能力等……… 以上三类合计估计125分左右! 第14题、第18和19题的第3问(约25分)属于难题,考查综合能力,发挥选拔功能。
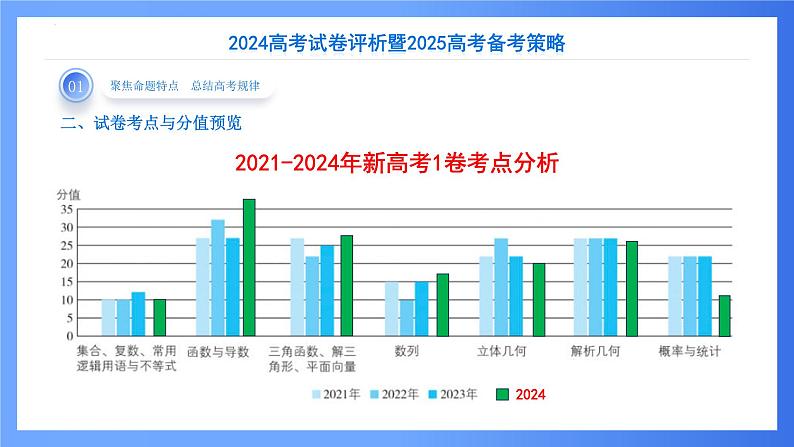
2021-2024年新高考1卷考点分析
二、试卷考点与分值预览
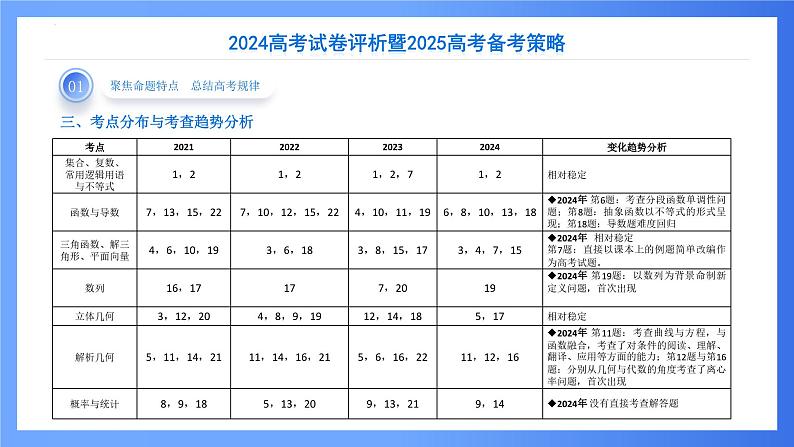
三、考点分布与考查趋势分析
1、立足主干知识,重点知识重点考查、甚至多次考查;2、非主干知识部分、三角、平面向量一如既往的稳定,为整套试卷的基础部分做了托底,立体几何、解析几何承载着中档题部分;3、函数与导数、立体几何、解析几何作为考查学生数学抽象、逻辑推理、直观想象、数学运算、数学建模等核心素养的重要载体,考查的越来越重,教材在课时方面也占有大量的比重,将一直是考查的重点,需要重点关注。4、日常教学和高考复习备考的过程中带领学生回归教材,理解数学本质,抓住数学概念的本质才能根本性的解决数学问题,真正提升学生的素养,减负增效。5、新定义问题,其本质是对数学概念、原理的理解并运用问题,未来可能是一种趋势,需要加以重视,在高一、高二阶段的教学过程中,不能只给结论,要重视概念的生成、公式定理的推导、探究应用的过程。
利用导函数研究函数的极值、单调性、大小比较
分段函数的单调性求参数
研究函数的性质,利用函数性质求参数、比较大小是历年的热点问题
2019版人教必修第二册 237页 第五章三角函数 例1
考查作图能力、数形结合
本题考查抽象函数,考查逻辑推理能力,本题可以看到斐波那契数列的背景。
f(1)=1 , f(2)=2,f(3)> f(2)+f(1)=3,f(4)> f(3)+f(2)>5,f(5)>f(4)+f(3)>8,f(6)>f(5)+f(4)>13,f(7)>f(6)+f(5)>21,f(8)>f(7)+f(6)>34,f(9)>f(8)+f(7)>55,f(10)> f(9)+f(8)>89,f(11)>f(10)+f(9)>144 ,f(12)> f(11)+f(10)>233,f(13)> f(12)+f(11)>377,f(14)>f(13)+f(12)>610 ,f(15)>f(14)+f(13)>987,f(16)>1000,所以f(20)>1000,选B.
抽象函数是近几年的热点问题,抽象函数是考察学生函数性质最深刻和有力的工具,可以从等式、不等式等多方面进行命题,考查对函数本质的理解。我们习惯上都是研究具体函数的性质,对抽象函数常见性质的证明和探索方法很容易忽略,这很可能是教学中的盲区!
抽象函数的考点考法发生变化!
通法:分别设切点,各自求切线方程,对比斜率和截距,得到方程再求解
破题点:甲选1时,甲一定输
恰当分类,一一罗列,不重不漏
在一套试题里两次考查离心率问题,属于首次
起点低,入口宽,方法多,计算量有一点大
(2)方法1:建立空间直角坐标系
(2)方法2:传统方法,作出二面角
多想少算—— 提升思维,考查素养
入口宽,方法多,适合不同学生
解:(1) 当1≤i
当m ≥ 4,数列{ an}至少有4×4+2=18项.去掉去掉a2,a13后剩下4m项,可将它们平均分成m组如下: a1,a4,a7,a10; a3,a6,a9,a12; a5,a8,a11,a14,剩余的m-3组依次为: a15,a16,a17,a18; a19,a20,a21,a22;…; a4m-1,a4m,a4m+1,a4m+2,这时,依定义,数列a1,a2,a3,…,a4m+1,a4m+2是(2,13)—可分数列.综上所述,当m≥3时,数列a1,a2,…,a4m+2是(2,13)一可分数列.
以考促教 教考衔接 2024年九省联考试卷评析及高考备考策略
注重对教材上的概念、公式、定理等数学知识的深刻理解,理解数学问题的本质。对概念、公式、定理等进行复盘,不留知识盲点,进一步夯实基础,确保基础部分不丢分。
1.回归教材,夯实基础
非主干知识:集合与简易逻辑、复数、平面向量、不等式主干知识: (1)三角:三角函数的图像与性质、三角恒等变换、解三角形。 (2)数列:等差、等比数列,数列求通项、求和,留意数列与其他知识交汇问题。 (3)立体几何:空间几何体的表面积、体积,点线面位置关系,用空间向量解决点线面的相关问题。 (4)解析几何:以基本性质、基本运算考查直线与圆、椭圆、双曲线、抛物线,突出直线和圆锥曲线的交点、弦长、轨迹、定值定点、最值范围等。 (5)概率与统计:概率计算、统计应用、数学期望,独立性检验和回归分析。 (6)函数与导数:函数的四大性质,函数模型的应用,应用导数知识解决函数问题是重点,经常与其他板块知识交汇融合考查。高考数学思想方法专题:函数与方程、数形结合、化归与转化、分类讨论思想方法
2.主干知识重点讲练,突出高考“热点”问题
3.精选例题、习题,直击要点
精选典型问题,精讲精练,讲练结合一切讲练,都要围绕学生展开,讲练太多,学生消化不了,落实不到学生身上。只有重质减量,才能抓好落实。当然减少练习量,不是指不做或少做,而是在精选试题上下功夫。
4.扎实复习,重难点突破
高考数学题量减少,中低档题目容易入手,拉不开差距,试题的压轴题难度会增加,拿分不易,要拿高分,必须攻克中难题。(1)不回避难点,对一轮复习过程中没有解决的问题进行重点突破,对问题的研究更深入一些,不要放弃解析几何和导数。(2)将难点问题逐一分解成小的问题,再逐一突破。
学生常见的问题及解决方案:
第一不计时,不作业。写作业的时候必须记时间。第二不总结,不作业。写完了作业后要总结一遍。第三不复习,不作业。写作业之前先复习一遍过。第四不检查,不作业。写完作业必须要去检查。第五不独立,不作业。写作业必须独立完成。第六不思考,不作业。面对难题,学生必须自己思考去攻克,最后才是求助老师!
1.指导学生规划好预习、听课、作业、课后总结等方面的要求
第一类:整理错题第二类:知识归纳第三类:题型总结第四类:解题技巧
有题目 有正解有错解 有错因有多解 有知识 有注释 有提醒
一题多解、多题一解,突出解法的发现和运用
直接法、筛选法(排除法)、特例法(特殊值,特殊图形,特殊位置,特殊函数)、数形结合法、验证法、估算法、特征分析法 、极限法、二级结论法等
3、指导学生掌握一些考试策略
(1)规划考试时间单选题1-3分钟、多选题2-5分钟、填空题2-4分钟,部分复杂小问可以暂时跳过,选填整体控制在45分钟以内;解答题由易到难,注意规范书写
(2)注意积累一些考试技巧先易后难,特殊值法、排除法、归纳总结法等
3.适当开展大中衔接,拓展视野
对于学有余力的同学,可以开展大中衔接,适度拓展学生的视野可以从从竞赛一试的题目中挑选一些能启迪思维的试题进行训练
4.注重数学思想方法的引导
函数与方程思想数形结合思想分类与整合思想:化归与转化思想特殊与一般思想:有限与无限的思想……
圆锥曲线中一类定值问题的探究
人教版选必一P121 探究
人教版选必一 P108 例3
思维进阶训练
分析:设点M (x,y),依题意:
人教版选必一 P1145 第11题
把上述一般结论添加上这两个定点后的轨迹称为圆,椭圆,双曲线(有心二次曲线)的统一定义。通过以上的探讨,我们可以得到如下的一些重要结论:
层级3:对于抛物线能否统一为两斜率乘积为定值的轨迹呢?
探索发现并不能统一,原因在于圆、椭圆、双曲线都是有心圆锥曲线,而抛物线不是有心圆锥曲线. 既然抛物线不能用两斜率乘积表示,那么能否用两斜率的其他运算来表示呢?
层级4:能否总结探究问题的一般研究方法?
对研究新定义问题的思考
新定义的压轴题主要考查的解决问题的能力,直接从猜想到论证,这个过程对于学生而言太快了,其实最主要的是“形成猜想”的过程。 新定义大题一般第一问都是一些例子,而学生们需要通过一些具体的例子,有意识的去“总结一些规律”才能形成猜想,如果发现不了新定义中的规律,是进行不下去的,这类问题的核心是“现象——规律(共性)——猜想原理——挖掘原因”大概这样一个逻辑。
1.举例子2.发现例子中的共性(题干让我们证的性质)3.挖掘产生这些共性的原因(核心) (1)正向挖掘:是什么原因导致了最后的共性 (2)反向挖掘:如果没有这个共性,为什么就不能得到题目要求的数列(或数表等)4.把这个过程抽象成数学语言书写出来
1,2,3,4,5,6
1,2,3,4,5,6,7,8,9,10,11,12,13,14
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22
1,4,7,10; 3,6,9,12; 5,8,11,14
功夫放在备课上,技巧放在选题上,落实放在训练上,提高放在讲评上。 ——华南师范大学赵萍教授
2024年高考数学新高考Ⅰ卷评析及备考策略(课件): 这是一份2024年高考数学新高考Ⅰ卷评析及备考策略(课件),共62页。
关于高考数学备考工作的几点建议 课件-2025届高三数学备考“0”诊,一轮复习策略: 这是一份关于高考数学备考工作的几点建议 课件-2025届高三数学备考“0”诊,一轮复习策略,共19页。PPT课件主要包含了今后的备考建议等内容,欢迎下载使用。
2024年高考数学三新背景下解析几何复习备考策略课件: 这是一份2024年高考数学三新背景下解析几何复习备考策略课件,共54页。PPT课件主要包含了解析化,算法优化,通性通法,数助形,形助数,巧用几何特征,强化作图意识,借助圆的几何性质求解,方法二定义视角优化,设而不求等内容,欢迎下载使用。












