广东省河源地区2023-2024学年七年级下学期期末数学试题（原卷版+解析版）

这是一份广东省河源地区2023-2024学年七年级下学期期末数学试题（原卷版+解析版），文件包含广东省河源地区2023-2024学年七年级下学期期末数学试题原卷版docx、广东省河源地区2023-2024学年七年级下学期期末数学试题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。

说明：1．全卷含答题卡共8页，满分120分，考试用时为120分钟．
2．本次考试范围：七年级下册内容．
3．答卷前，考生根据学校要求，人工批改学校考生在答题卡左侧横线处用黑色字迹的钢笔或签字笔填写学校、姓名、学号信息；网上阅卷学校无须填写，只需正确贴条形码信息即可．
4．选择题每小题选出答案后，用2B铅笔在答题卡上对应题目选项的信息点涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案，答案不能答在试题上．
5．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡指定区域内相应位置上．如需改动，先划掉原答案，然后再写上新的答案．答题卡不得使用透明胶或涂改液．不按以上要求作答的答案无效．
一、选择题（本大题共10小题，每小题3分，共30分）
1. 如图，的同位角是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了同位角，根据同位角的定义“两条直线被第三条所截，在截线的同旁，在被截线的同一方，我们把这种位置关系的角称为同位角”选择的同位角即可，熟练掌握同位角的定义判断是解题的关键．
【详解】解：根据同位角的定义可得的同位角是，
故选：C．
2. 下列手机中的图标是轴对称图形的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】本题主要考查了轴对称图形的定义：把一个图形沿着某一条直线折叠，如果直线两旁的部分完全重合，称这个图形为轴对称图形，这条直线叫做对称轴．
根据轴对称图形的概念，把图形沿某一条直线折叠，看直线两旁的部分是否能够互相重合，逐一进行判断即可．
【详解】A．不是轴对称图形，故此选项不合题意；
B．不是轴对称图形，故此选项不合题意；
C．是轴对称图形，故此选项符合题意；
D．不是轴对称图形，故此选项不合题意．
故选：C．
3. 很多人可能都知道蓝鲸是迄今发现的地球上最大的动物，却都不了解体积最小的动物，世界上体积最小的动物要比蚂蚁小很多倍，它是被命名为 H39的原生动物，它的最长直径也不过才米． 其中数据用科学记数法表示为（ ）
A. B. C. D.
【答案】C
【解析】
分析】本题考查科学记数法定义．根据题意利用科学记数法表示方法即可得到本题答案．
【详解】解：，
故选：C．
4. 下列运算正确的是（ ）
A B. C. D.
【答案】C
【解析】
【分析】本题考查了同底数幂的乘法，除法，幂的乘方及合并同类项，根据运算法则逐一判断即可．
【详解】解：A、，故错误，不符合题意；
B、，故错误，不符合题意；
C、，故正确，符合题意；
D、，故错误，不符合题意；
故选：C．
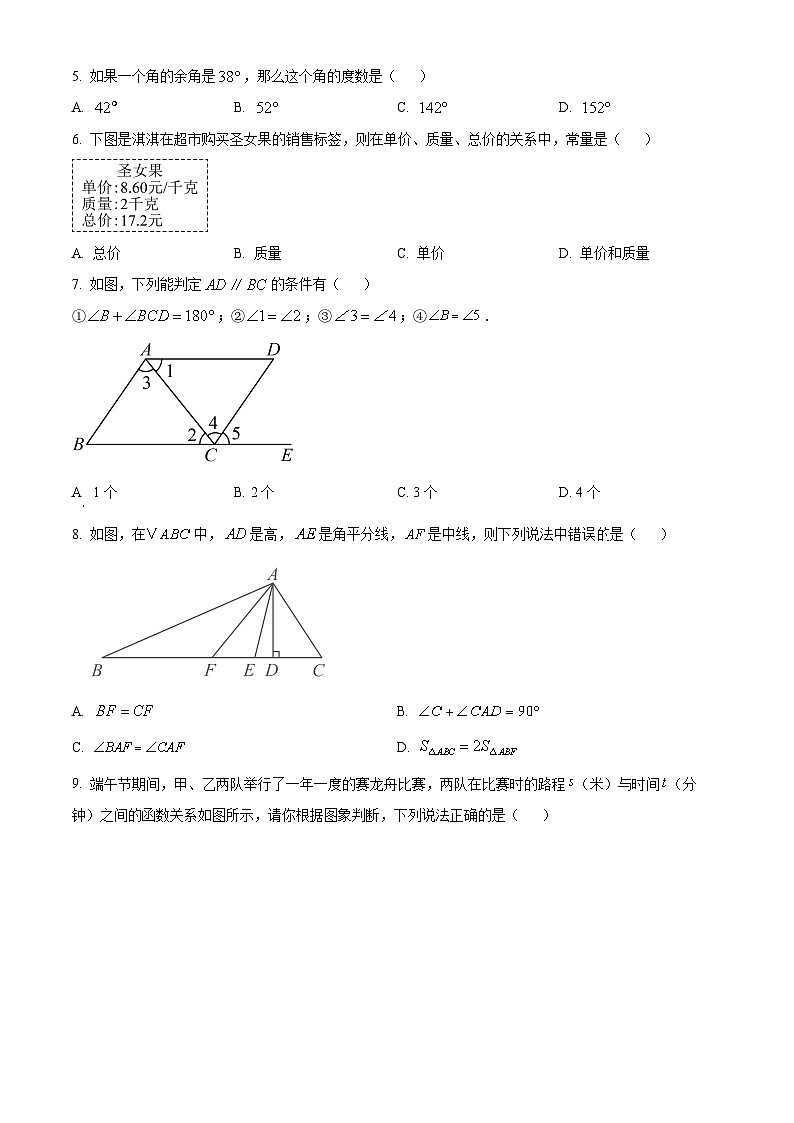
5. 如果一个角的余角是，那么这个角的度数是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】此题考查了余角，和为的两个角互为余角，据此解答即可．
【详解】解：∵，
∴如果一个角的余角是，那么这个角的度数是，
故选：B．
6. 下图是淇淇在超市购买圣女果的销售标签，则在单价、质量、总价的关系中，常量是（ ）

A. 总价B. 质量C. 单价D. 单价和质量
【答案】C
【解析】
【分析】本题考查变量和常量，根据在一个变化的过程中，固定不变的量为常量，进行判断即可．
【详解】解：在单价、质量、总价的关系中，单价是常量，总价随着质量的变化而变化，
故选C．
7. 如图，下列能判定的条件有（ ）
①；②；③；④．
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
【分析】本题考查平行线的判定，根据平行线的判定定理“同旁内角互补，两直线平行；内错角相等，两直线平行；同位角相等，两直线平行”逐项判断即可得出结论．
【详解】解：①，由“同旁内角互补，两直线平行”可判定，不能判定；
②，由“内错角相等，两直线平行”可判定；
③，由“内错角相等，两直线平行”可判定，不能判定；
④，由“同位角相等，两直线平行”可判定，不能判定；
综上可知，能判定的条件有1个，
故选A．
8. 如图，在中，是高，是角平分线，是中线，则下列说法中错误的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】本题考查了三角形的中线、高线及角平分线的意义，三角形一边上的中线平分此三角形的面积等知识．根据上述知识逐项进行判断即可．
【详解】解：∵是的中线，
，A说法正确，不符合题意；
是高，
，
，B说法正确，不符合题意；
是角平分线，
，而与不一定相等，C说法错误，符合题意；
，
，D说法正确，不符合题意；
故选：C．
9. 端午节期间，甲、乙两队举行了一年一度的赛龙舟比赛，两队在比赛时的路程（米）与时间（分钟）之间的函数关系如图所示，请你根据图象判断，下列说法正确的是（ ）
A. 甲队率先到达终点B. 甲队比乙队多走了200米
C. 乙队的速度始终比甲队的速度大D. 乙队比甲队少用0.2分钟
【答案】D
【解析】
【分析】根据函数图象所给的信息，逐一判断．
【详解】解：A、由函数图象可知，甲走完全程需要4分钟，乙走完全程需要3.8分钟，乙队率先到达终点，本选项错误；
B、由函数图象可知，甲、乙两队都走了1000米，路程相同，本选项错误；
C、根据分钟的时间段图象可知，甲队的速度比乙队的速度快，本选项错误；
D、因为分钟，所以，乙队比甲队少用0.2分钟，本选项正确；
故选：D．
【点睛】本题考查了函数图象的读图能力．解题的关键是要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．
10. 如图，为的中线，为的中线，为的中线，…，按此规律，为的中线，若的面积为1，则的面积为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查了三角形的面积公式，三角形的中线，找规律，根据三角形的中线把三角形的面积分成了相等的两部分进行解答即可得；理解题意，根据三角形的中线找出规律是解题的关键．
【详解】解：∵为的中线，的面积为1，
∴，
∵为的中线，，
∴，
∵为的中线，，
∴，
…
按此规律，为的中线，则的面积为：，
故选：D．
二、填空题（每小题3分，共15分）
11. 计算：______．
【答案】17
【解析】
【分析】本题主要考查了零指数幂运算和负整数指数幂运算，熟练掌握相关运算法则是解题关键．首先根据零指数幂运算法则和负整数指数幂运算法则进行运算，然后求和即可．
【详解】解：．
故答案为：17．
12. 小球在如图所示的地板上自由滚动最终停在黑色区域的可能性是______．
【答案】
【解析】
【分析】本题考查几何概率，解题的关键是熟练掌握几何概率的求法，先求出黑色方砖在整个地板中所占的比值，再根据其比值即可得出结论．
【详解】解：∵由图可知，黑色方砖3块，共有9块方砖，
∴黑色方砖在整个地板中所占的比值，
∴小球停留在黑色区域的概率是．
故答案为：．
13. 如图，已知，那么______．

【答案】95
【解析】
【分析】此题主要考查了全等三角形的性质，三角形内角和定理，直接利用全等三角形的性质得出的度数，进而得出答案．
【详解】解：∵，
，
．
故答案为：95．
14. 如图，直线交于点平分，若，则______．
【答案】105
【解析】
【分析】本题考查了平角的定义，对顶角的定义及角平分线的定义，熟练掌握知识点是解题的关键，先由邻补角的定义得出，再根据角平分线的定义得出，最后对顶角的定义得到，由计算即可．
【详解】解：，，
，
平分，
，
，
，
故答案为：．
15. 把一张长方形纸片沿折叠后，与的交点为，、分别在、的位置上，若，则_________．
【答案】12
【解析】
【分析】根据折叠的性质及平行线的性质可分别求得∠2与∠1的度数，则可求得结果数．
【详解】∵AD∥BC，∠EFG=48°，
∴∠DEF=∠EFG=48°，∠2=∠GED=∠DEF+∠GEF．
由折叠的性质知：∠GEF=∠DEF=48°，
则，∠2=48°+48°=96°，
∴，
故答案为：12．
【点睛】本题考查了平行线的性质、折叠的性质，掌握这两个性质是关键．
三、解答题（本大题共9小题，共75分）
16. 利用平方差公式计算：．
【答案】
【解析】
【分析】本题考查了平方差公式，将表示为，将表示为，从而利用平方差进行计算即可，解答本题关键是掌握平方差公式的形式．
【详解】解：原式
．
17. 已知：线段a，c，．求作：．使，，．（要求：尺规作图，不写作法，保留作图痕迹）

【答案】见解析
【解析】
【分析】首先根据一个角等于已知角的方法作，再在角的两边分别截取，，再连接．
【详解】解：如图所示：
【点睛】此题主要考查了复杂作图，关键是掌握作一个角等于已知角的方法．
18. 先化简，再求值：，其中．
【答案】，
【解析】
【分析】此题考查了整式的混合运算—化简求值，先根据单项式乘以多项式和多项式除以单项式运算法则进行化简，再把代入计算即可，解题的关键是熟练掌握相关运算法则．
【详解】解：原式
，
当时，
原式．
19. 小亮和妈妈去超市买凳子，小亮发现把凳子按如图方式叠放在一起时，每叠放一个凳子，增加的高度是一样的．下表是叠放凳子的总高度与凳子数量的几组对应值．
根据以上信息，回答下列问题：
（1）按照表格所示的规律，当凳子的数量为6时，叠放的凳子总高度为______厘米；
（2）按照表格所示的规律，写出叠放的凳子总高度h与凳子的数量n之间的关系式______；
（3）按照表格所示的规律，若将该种凳子按如图方式叠放在层高为92厘米的超市货架上，能叠放11张凳子吗？说明理由．
【答案】（1）70 （2）（是正整数）
（3）不能能叠放11个．理由见解析
【解析】
【分析】本题考查一次函数的应用，有理数四则混合运算的应用，找到数据变化的规律并求出函数关系式是解题的关键．
（1）每叠放一个凳子，增加的高度是5厘米，据此作答即可；
（2）根据“总高度的增加量凳子数量每叠放一个凳子增加的高度”写出h与n的关系式，并标明n的取值范围即可；
（3）将代入（2）中得到的关系式，求出对应h的值并与92比较大小即可得出结论．
【小问1详解】
解：由表格中的数据可知，凳子数量每增加1，叠放凳子的总高度就增加5，
当凳子的数量为6时，叠放的凳子总高度为厘米，
故答案为：70；
【小问2详解】
解：由题意得，
故答案为：（是正整数）；
【小问3详解】
解：不能能叠放11个．理由如下：
当时，，
不能叠放11个．
20. 如图，有一个可以自由转动的转盘，转盘被平均分成等份，每个扇形区域内分别标有这六个数字，转动转盘，当转盘停止转动后，指针指向的数字即为转出的数字．
请回答下列问题：
（1）随机转动转盘，转出数字是______事件，转出数字是______事件；（从“随机”，“必然”，“不可能”中选一个填空）
（2）随机转动转盘，转出的数字是奇数的概率是______；
（3）现有两张分别写有和的卡片，随机转动转盘，转盘停止转动后，将转出的数字与两张卡片上的数字分别作为三条线段的长度，则这三条线段能构成三角形的概率是多少？请说明理由．
【答案】（1）不可能，随机；
（2）；
（3），见解析．
【解析】
【分析】（）根据“不可能事件”“随机事件”“必然事件”的意义进行判断即可；
（）转动转盘一次，共有种等可能出现的结果情况，其中转出的数字是奇数的有种，根据概率公式即可求解；
（）转动转盘可得到这六个数字中的一个，与卡片中的两个数字作为三条线段的长度，共有种等可能的情况，其中能构成三角形的有种，根据概率公式即可求解；
本题考查了随机事件，概率的计算，三角形三边关系，熟练掌握知识点的应用是解题的关键．
【小问1详解】
∵转盘被平均分成等份，分别标有这六个数字，没有数字，
∴“转出数字”是不可能的，转出数字是可能的，
故答案为：不可能事件，随机事件；
【小问2详解】
转动转盘一次，共有种等可能出现的结果情况，其中转出的数字是奇数的有种，
∴转出的数字是奇数的概率是，
故答案为：；
【小问3详解】
这三条线段能构成三角形的概率是，理由如下：
设转出的数字是，则共有种等可能的结果，
∵能构成三角形，
∴，
∴转盘中符合结果数为种，
∴这三条线段能构成三角形的概率是．
21. 如图，已知是的平分线，交于点，点分别是上的点，且．
（1）图中与是一对______，与是一对______；（填“同位角”或“内错角”或“同旁内角”）
（2）若，垂足为，则的度数为______；
（3）判断与是什么位置关系？说明理由．（请补充完整下面的推理过程）
解：______，理由如下：
，（已知）
______，（同位角相等，两直线平行）
，（______）
，（已知）
______，（等量代换）
______．（______）
【答案】（1）同旁内角；内错角
（2）
（3）见解析
【解析】
【分析】本题考查了同位角，内错角，同旁内角，平行线的判定和性质，直角三角形的特征，角的平分线，熟练掌握平行线的判定和性质是解题的关键．
（1）根据同位角，内错角，同旁内角的定义，结合图形判断解答即可．
（2）根据，判定，结合，，利用平行线的性质，直角三角形的两个锐角互余性质计算即可．
（3）根据平行线的判定和性质，推理证明即可．
【小问1详解】
解：根据定义，判定与是一对同旁内角，与是一对内错角，
故答案为：同旁内角；内错角．
【小问2详解】
解：如图，∵，
∴，
∴，
∵，，
∴，
故答案为：．
【小问3详解】
解：，理由如下：
，（已知）
，（同位角相等，两直线平行）
，（两直线平行，内错角相等）
，（已知）
，（等量代换）
．（同旁内角互补，两直线平行）
故答案为：，；两直线平行，内错角相等；；；同旁内角互补，两直线平行．
22. 如图，在中，为上一点，为中点，连接并延长至点，使得．
（1）求证：；
（2）连接，若平分平分，且，求的度数．
【答案】（1）见解析 （2）
【解析】
【分析】本题考查全等三角形的判定和性质，平行线的性质，角平分线有关的计算．解题的关键是证明三角形全等．
（1）先证明，得到，即可得证；
（2）利用平行线的性质和角平分线的定义，求出的度数，再根据角平分线定义，即可得解．
【小问1详解】
证明：中点，
，
．
，
在和中，
；
【小问2详解】
解：平分
，
．
平分，
，
．
23. 阅读理解：
若满足，求的值．
解：设，，
则，，
∴
（1）【类比探究】若满足．求的值；
（2）【联系拓展】若满足，则______；（直接写出结论，不用说明理由．）
（3）【解决问题】如图，在长方形中，，，点是上的点，且，分别以为边在长方形外侧作正方形和正方形，若长方形的面积为平方单位，则图中阴影部分的面积和为多少平方单位？
【答案】（1）；
（2）；
（3）阴影部分的面积和为平方单位．
【解析】
【分析】（）根据题目提供的方法，进行计算即可；
（）设，，则，，然后利用进行计算即可；
（）由题意得，，，则阴影部分的面积和为，由长方形的面积为平方单位得，设，，根据即可求解；
本题考查了完全平方公式的几何背景，解题的关键是掌握完全平方公式的结构特征，熟练掌握，，与间的关系．
【小问1详解】
设，，
则，，
所以，
，
，
；
【小问2详解】
设，，
则，，
所以，
，
，
，
故答案为：；
【小问3详解】
由题意得，，，
∴阴影部分的面积和为，
∵长方形的面积为，
∴，
∴，
设，，
则，，
∴
，
，
；
∴阴影部分的面积和为平方单位．
24. 综合与实践：数学社团的同学以“两条平行线（）和一块含角的直角三角板”为主题开展数学活动，已知点不能同时落在直线和之间．
（1）【探究】如图1，把三角板的角的顶点分别放在上，若，求的度数；
（2）【迁移】如图2，把三角板的锐角顶点放在上，且保持不动，绕点转动三角板，若点恰好落在和之间，且与所夹锐角为，求的度数；
（3）【拓展】把三角板的锐角顶点放在上，在绕点旋转三角板的过程中，若，请直接写出射线与相交所夹锐角的度数．
【答案】（1）；
（2）；
（3）或．
【解析】
【分析】此题主要考查了平行线的性质，角的计算，准确识图，熟练掌握平行线的性质，角的计算是解决问题的关键．
（1）依题意得：，由，得出，
再得出，即可求解；
（2）过点E作，得到，得出，，即可求解；
（3）分两种情况讨论如下：①当点E在上方时，当点E在下方时，分别求解即可．
【小问1详解】
解：依题意得：，
，
，
，
，
，
．
【小问2详解】
解：如图，过点E作，
依题意得：，
，
，
，
，
，
．
【小问3详解】
解：分两种情况讨论如下：
①当点E在上方时，设交于点H，如图所示：
依题意得：，
设，则，
，
，
解得：，
，
，
；
当点E在下方时，延长交于点H，如图所示：
依题意得：，
设，则，
，
，
，
解得：，
，
，
综上所述：射线与相交所夹锐角的度数为或．凳子数量（张）
1
2
3
4
…
叠放凳子的总高度（厘米）
45
50
55
60
…