











第十章 §10.7 概率与统计的综合问题-2025年新高考数学一轮复习(课件+讲义+练习)
展开1、揣摩例题。课本上和老师讲解的例题,一般都具有一定的典型性和代表性。要认真研究,深刻理解,要透过“样板”,学会通过逻辑思维,灵活运用所学知识去分析问题和解决问题,特别是要学习分析问题的思路、解决问题的方法,并能总结出解题的规律。 2、精练习题。复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。 3、加强审题的规范性。每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。 4、重视错题。“错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
§10.7 概率与统计的综合问题
例1 (2023·上饶模拟)为了解某高校学生每天的运动时间,随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生每天平均运动时间(单位:分钟)的频率分布直方图,将每天平均运动时间不低于40分钟的学生称为“运动族”.
题型一 频率分布直方图与分布列的综合问题
(1)用样本估计总体,已知某学生每天平均运动时间不低于20分钟,求该学生是“运动族”的概率;
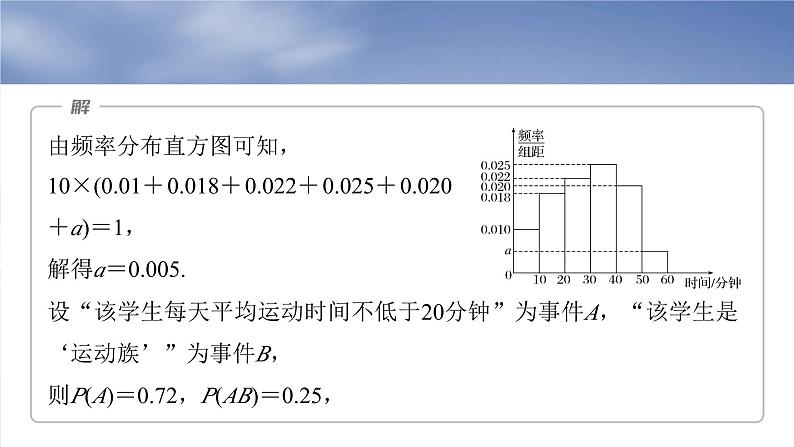
由频率分布直方图可知,10×(0.01+0.018+0.022+0.025+0.020+a)=1,解得a=0.005.
设“该学生每天平均运动时间不低于20分钟”为事件A,“该学生是‘运动族’”为事件B,则P(A)=0.72,P(AB)=0.25,
所以在该学生每天平均运动时间不低于20分钟的条件下是“运动族”的概率为
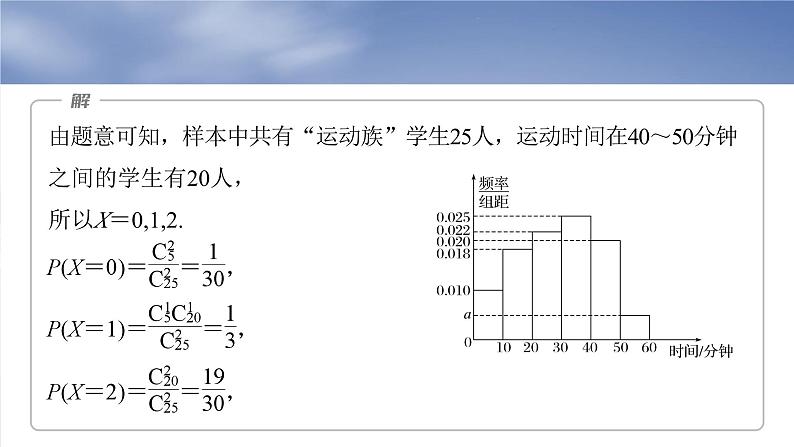
(2)从样本里的“运动族”学生中随机选取两位同学,用随机变量X表示每天平均运动时间在40~50分钟之间的学生数,求X的分布列及期望.
由题意可知,样本中共有“运动族”学生25人,运动时间在40~50分钟之间的学生有20人,所以X=0,1,2.
高考常将频率分布直方图与分布列等交汇在一起进行考查,解题时要正确理解频率分布直方图,能利用频率分布直方图正确计算出各组数据.概率问题以计算为主,往往和实际问题相结合,要注意理解实际问题的意义,使之和相应的概率计算对应起来.
跟踪训练1 (2023·呼和浩特模拟)某高校共有15 000人,其中男生10 500人,女生4 500人,为调查该校学生每周平均体育运动时间的情况,采用按比例分配的分层随机抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).(1)应收集多少个女生样本数据?
因为该校共有15 000人,其中女生有4 500人,
又因为采用按比例分配的分层随机抽样的方法收集300位学生的样本数据,
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组的区间为[0,2),[2,4),[4,6),[6,8),[8,10),[10,12].请估计该校学生每周平均体育运动时间不低于4个小时的概率;
由频率分布直方图可知,学生每周平均体育运动时间不低于4个小时的频率为(0.15+0.125+0.075+0.025)×2=0.75,故估计该校学生每周平均体育运动时间不低于4个小时的概率为0.75.
(3)视样本数据的频率为概率,现从全校随机抽取4名学生,记X为这4名学生中运动时间不低于4个小时的人数,求X的分布列以及数学期望.
题型二 回归模型与分布列的综合问题
例2 (2023·韶关模拟)研究表明,如果温差大,且人们不注意保暖,可能会导致自身受到风寒刺激,增加感冒患病概率,特别是对于儿童以及年老体弱的人群,要多加防范.某中学数学建模社团成员研究了昼夜温差大小与某小学学生新增感冒就诊人数之间的关系,他们记录了某六天的温差,并到校医室查阅了这六天中每天学生新增感冒就诊的人数,得到数据如下:
(1)已知第一天新增感冒就诊的学生中有4位男生,从第一天新增感冒就诊的学生中随机抽取2位,其中男生人数记为X,若抽取的2人中至少有一位女生的概率为 ,求随机变量X的分布列和数学期望;
所以y1(y1-1)=4×3×6=9×8,解得y1=9,即第一天新增感冒就诊的学生有9位,其中男生4位,女生5位,则随机变量X的所有可能取值为0,1,2,且X服从超几何分布,其中N=9,M=4,n=2,
据此估计昼夜温差为15°C时,该校新增感冒就诊的学生人数为35.
高考常将回归模型与分布列等交汇在一起进行考查,求经验回归方程时要充分利用已知数据,合理利用公式减少运算.求解概率问题时要注意概率模型的应用,明确所求问题所属的事件类型是关键.
跟踪训练2 (2023·武汉模拟)某企业计划新购买100台设备,并将购买的设备分配给100名年龄不同(视为技术水平不同)的技工加工一批模具,因技术水平不同而加工出的产品数量不同,故产生的经济效益也不同.若用变量x表示不同技工的年龄,变量y为相应的效益值(元),根据以往统计经验,他们的工作效益满足最小二乘法,且y关于x的经验回归方程为 =1.2x+40.6.(1)试预测一名年龄为52岁的技工使用该设备所产生的经济效益;
所以预测一名年龄为52岁的技工使用该设备所产生的经济效益为103元.
(2)试根据样本相关系数r的值判断使用该批设备的技工人员所产生的效益与技工年龄的相关程度(若0.75≤|r|≤1,则认为y与x的线性相关程度很强;若|r|<0.75,则认为y与x的线性相关程度不强);
因为0.75<0.88<1,所以y与x的线性相关程度很强.所以使用该批设备的技工人员所产生的效益与技工年龄的相关程度很强.
(3)若这批设备有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.02,0.03.若两道工序都没有出现故障,则生产成本不增加;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.求这批设备增加的生产成本的期望.
设增加的生产成本为ξ(万元),则ξ的可能取值为0,2,3,5.P(ξ=0)=(1-0.02)×(1-0.03)=0.950 6,P(ξ=2)=0.02×(1-0.03)=0.019 4,P(ξ=3)=(1-0.02)×0.03=0.029 4,P(ξ=5)=0.02×0.03=0.000 6.所以E(ξ)=0×0.950 6+2×0.019 4+3×0.029 4+5×0.000 6=0.13,所以这批设备增加的生产成本的期望为0.13万元.
题型三 独立性检验与分布列的综合问题
例3 (2023·聊城模拟)某中学在高一学生选科时,要求每位学生先从物理和历史这两个科目中选定一个科目,再从思想政治、地理、化学、生物这四个科目中任选两个科目.选科工作完成后,为了解该校高一学生的选科情况,随机抽取了部分学生作为样本,对他们的选科情况统计后得到下表:
(1)利用上述样本数据填写右列2×2列联表,并依据小概率值α=0.001的独立性检验,分析以上两类学生对生物学科的选法是否存在差异;
由题意可得选择物理类的总人数为300,其中选择生物学科的人数为180,不选择生物学科的人数为120;选择历史类的总人数为200,其中选择生物学科的人数为80,不选择生物学科的人数为120,据此完善2×2列联表如右:
零假设为H0:两类学生对生物学科的选法没有差异.由表中数据可得
根据小概率值α=0.001的独立性检验可知零假设不成立,即可以认为两类学生对生物学科的选法存在差异,且此推断犯错误的概率不大于0.001.
(2)假设该校高一所有学生中有 的学生选择了物理类,其余的学生都选择了历史类,且在物理类的学生中其余两科选择的是地理和化学的概率为 ,而在历史类的学生中其余两科选择的是地理和化学的概率为 .若从该校高一所有学生中随机抽取100名学生,用X表示这100名学生中同时选择了地理和化学的人数,求随机变量X的均值E(X).
记“学生选择物理类”为事件M,“学生选择历史类”为事件N,“同时选择地理和化学”为事件C,
高考常将独立性检验与分布列等交汇在一起进行考查,解决独立性检验问题,要注意过好“三关”:假设关、公式关、对比关.解决概率问题要准确地把握题中所涉及的事件,明确所求问题所属的事件类型.
跟踪训练3 (2024·沈阳模拟)随着科技的进步和人民生活水平的提高,电脑已经走进了千家万户,成为人们生活、学习、娱乐的常见物品,便携式电脑(俗称“笔记本”)也非常流行.某公司为了研究“台式机”与“笔记本”的受欢迎程度是否与性别有关,在街头随机抽取了50人做调查研究,调查数据如下表所示.
(1)依据小概率值α=0.01的独立性检验,分析喜欢哪种机型与性别是否有关?
零假设为H0:喜欢哪种机型与性别无关.
根据小概率值α=0.01的独立性检验可知零假设不成立,即可以认为喜欢哪种机型与性别有关,且此推断犯错误的概率不大于0.01.
(2)该公司针对男性客户做了调查,某季度男性客户中有青年324人,中年216人,老年108人,用按比例分配的分层随机抽样的方法选出12人,又随机抽出3人进行答谢,这3人中的青年人数设为随机变量X,求X的分布列与数学期望.
由题意,324∶216∶108=3∶2∶1,所以12人中有青年人6人,中年人4人,老年人2人,则X的所有可能取值为0,1,2,3,
1.(2023·泰州模拟)第二十二届卡塔尔世界杯足球赛决赛中,阿根廷队通过扣人心弦的点球大战战胜了法国队.某校为了丰富学生课余生活,组建了足球社团.足球社团为了解学生喜欢足球是否与性别
有关,随机抽取了男、女学生各100名进行调查,部分数据如表所示:(1)根据所给数据完成上表,并依据小概率值α=0.001的独立性检验,分析该校学生喜欢足球与性别是否有关?
零假设为H0:该校学生喜欢足球与性别无关.
根据小概率值α=0.001的独立性检验可知零假设不成立,即该校学生喜欢足球与性别有关,且此推断犯错误的概率不大于0.001.
(2)社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知男生进球的概率为 ,女生进球的概率为 ,每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.
3人进球总次数ξ的所有可能取值为0,1,2,3,
2.某地区区域发展指数评价指标体系基于五大发展理念构建,包括创新发展、协调发展、绿色发展、开放发展和共享发展5个一级指标.该地区区域发展指数测算方法以2015年作为基期并设指数值为100,通过时序变化,观察创新发展、协调发展、绿色发展、开放发展和共享发展5个分领域指数值的变动趋势.分别计算创新发展、协调发展、绿色发展、开放发展和共享发展5个分指数,然后合成为该地区区域发展总指数,如下图所示.
若x(2015年记为x=1,2016年记为x=2,依此类推)与发展总指数y存在线性关系.(1)求x与发展总指数y的经验回归方程;
(2)若规定发展总指数大于115的年份为和谐发展年,和谐发展年中发展总指数低于130的视为良好,记1分,发展总指数大于130的视为优秀,记2分,从和谐发展年中任取三年,用X表示记分之和,求X的分布列和数学期望.
由题可知,和谐发展年有5个,其中计分为1分的年份有3个,计分为2分的年份有2个,X的所有可能取值为3,4,5,
3.(2023·南京模拟)渔船海上外出作业受天气限制,尤其浪高对渔船安全影响最大,二月份是某海域风浪最平静的月份,浪高一般不超过3 m.某研究小组从前些年二月份各天的浪高数据中,随机抽取50天数据作为样本,制成频率分布直方图(如图).根据海浪高度将海浪划分为如下等级:
海事管理部门规定:海浪等级在“大浪”及以上禁止渔船出海作业.
(1)某渔船出海作业除受浪高限制外,还受其他因素影响,根据以往经验可知,“微浪”情况下出海作业的概率为0.9,“小浪”情况下出海作业的概率为0.8,“中浪”情况下出海作业的概率为0.6,
请根据上面频率分布直方图,估计二月份的某天各种海浪等级出现的概率,并求该渔船在这天出海作业的概率;
记这天浪级是“微浪”为事件A1,浪级是“小浪”为事件A2,浪级是“中浪”为事件A3,浪级是“大浪”为事件A4.该渔船当天出海作业为事件B,则由题意可知,P(A1)=50×0.004=0.2,P(A2)=50×0.006=0.3,P(A3)=50×0.004+50×0.002=0.3,P(A4)=50×0.002+50×0.002=0.2,
∴P(B)=P(BA1)+P(BA2)+P(BA3)=P(B|A1)P(A1)+P(B|A2)P(A2)+P(B|A3)P(A3)=0.9×0.2+0.8×0.3+0.6×0.3=0.18+0.24+0.18=0.6.
(2)气象预报预计未来三天内会持续“中浪”或“大浪”,根据以往经验可知,若某天是“大浪”,则第二天是“大浪”的概率为 ,“中浪”的概率为 ;若某天是“中浪”,则第二天是“大浪”的概率
为 ,“中浪”的概率为 .现已知某天为“中浪”,记该天的后三天出现“大浪”的天数为X,求X的分布列和数学期望.
依题意可知,X的所有可能取值为0,1,2,3,
4.(2024·葫芦岛模拟)某地相继爆发了甲型H1N1流感病毒(甲流)和诺如病毒感染潮,为了了解感染病毒类型与年龄的关系,某市疾控中心随机抽取了部分感染者进行调查.据统计,甲流患者数是诺如病毒感染者人数的2倍,在诺如病毒感染者中60岁以上患者占 ,在甲流患者中60岁以上的人数是其他人数的一半.(1)若根据小概率值α=0.005的独立性检验,能认为“感染病毒的类型与年龄有关”,则抽取的诺如病毒感染者至少有多少人?
设感染诺如病毒的患者为x人,则感染甲流的患者为2x人,
由题意必有χ2≥7.879,
又因为x为整数,故抽取的诺如病毒感染者至少有27人.
(2)研究发现,针对以上两种病毒比较有效的药物是奥司他韦和抗病毒口服液,并且发现奥司他韦治疗以上两种病毒有效的概率是抗病毒口服液的2倍.现对两种药物进行临床试验,对抗病毒口服液共进行两轮试验,每轮试验中若连续2次有效或试验3次时,本轮试验结束;对奥司他韦先进行3次试验,若至少2次有效,则试验结束,否则再进行3次试验后方可结束,假定两种药物每次试验是否有效均相互独立,且两种药物的每次试验费用相同.请结合以上针对两种药物的临床试验方案,估计哪种药物的试验费用较低?
设抗病毒口服液治疗有效的概率为p,每次试验花费为m,
设抗病毒口服液试验总花费为X,X的所有可能取值为4m,5m,6m,P(X=4m)=p4,P(X=5m)=2(p2-p4),P(X=6m)=(1-p2)2,故E(X)=4mp4+10m(p2-p4)+6m(p4-2p2+1)=-2mp2+6m,设奥司他韦试验总花费为Y,Y的所有可能取值为3m,6m,
第十章 必刷大题20 概率与统计-2025年新高考数学一轮复习(课件+讲义+练习): 这是一份第十章 必刷大题20 概率与统计-2025年新高考数学一轮复习(课件+讲义+练习),文件包含第十章必刷大题20概率与统计pptx、第十章必刷大题20概率与统计教师版docx、第十章必刷大题20概率与统计笔刷专练docx等3份课件配套教学资源,其中PPT共43页, 欢迎下载使用。
新高考数学一轮复习讲练课件10.6 概率与统计的综合问题(含解析): 这是一份新高考数学一轮复习讲练课件10.6 概率与统计的综合问题(含解析),共31页。
广东专用2024版高考数学大一轮总复习第九章概率与统计综合突破六概率与统计综合问题课件: 这是一份广东专用2024版高考数学大一轮总复习第九章概率与统计综合突破六概率与统计综合问题课件,共60页。PPT课件主要包含了核心考点精准突破,课时作业知能提升等内容,欢迎下载使用。












