2023-2024学年辽宁省辽阳市八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年辽宁省辽阳市八年级（下）期末数学试卷（含答案），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.用不等式表示：x2是非负数，则下列各式中正确的是( )
A. x2>0B. x2≥0C. x2≠0D. x2≤0
2.下列从左到右的变形中，属于多项式因式分解的是( )
A. 2a2b−3ab2=ab(2a−3b)B. (x+1)(x−3)=x2−2x−3
C. x2−3=(x+1)(x−1)−2D. 10a2b=2a⋅5ab
3.2023年2月24日，“逐梦寰宇问苍穹——中国载人航天工程三十年成就展”在中国国家博物馆展出，下列航天图标中，是中心对称图形的是( )
A. B.
C. D.
4.关于x的方程k+3x−2+1=3xx−2有增根，则k的值是( )
A. 0B. 2C. −3D. 3
5.如图，在△ABC中，∠C=90°，∠B=30°，D是BC上一点，连接AD，若AD平分∠BAC，设△ADB和△ADC的面积分别是S1，S2，则S1：S2=( )
A. 1：1
B. 2：1
C. 3：1
D. 3：2
6.若b>a>0，则下列各式正确的是( )
A. ab=a+1b+1B. ab>a+1b+1C. ab7.已知△ABC的三边长分别为a，b，c，且满足a2−ac=b2−bc，则△ABC一定是( )
A. 直角三角形B. 等边三角形C. 锐角三角形D. 等腰三角形
8.指出下列命题中的假命题( )
A. 三个角都相等的三角形是等边三角形
B. 一条直角边相等且另一条直角边上的中线也相等的两个直角三角形全等
C. 三角形的三条角平分线相交于一点，并且这点到三个顶点的距离相等
D. 两组对角分别相等的四边形是平行四边形
9.如图，把△ABC绕着点C顺时针旋转，使点B落在点B′的位置，点A的对应点是点A′，连接BB′，若BB′//AC，∠A′CB=45°，则∠ACA′的度数是( )
A. 22.5°
B. 25°
C. 28°
D. 30°
10.如图，▱ABCD的对角线AC与BD相交于点O，E、F是对角线BD上不同的两点，下列条件中，不能得出四边形AECF一定为平行四边形的是( )
A. BE=DFB. ∠BAE=∠DCF
C. AF//CED. AE=CF
二、填空题：本题共5小题，每小题3分，共15分。
11.若分式x−3x+2有意义，则x的取值范围是______．
12.因式分解：(a2+b2)2−4a2b2= ______．
13.一个多边形的内角和是它的外角和的5倍，则这个多边形的边数为______．
14.如图，在▱ABCD中，F是BC边上一点，E是CD边的中点，AE平分∠DAF.若BF=6，CF=2，则AF的长为______．
15.如图，在▱ABCD中，分别以AB、AD为边向外作等边△ABE、等边△ADF，延长CB交线段AE于点G，连接CE、CF、EF，则在以下四个结论中，①△CDF≌△EBC；②CG⊥AE；③∠CDF=∠EAF；④△ECF是等边三角形．
一定正确的有：______.(只填序号)
三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
先化简，再求值：(1x2−x+x−3x2−1)÷x−1x2+2x+1，其中x=−3．
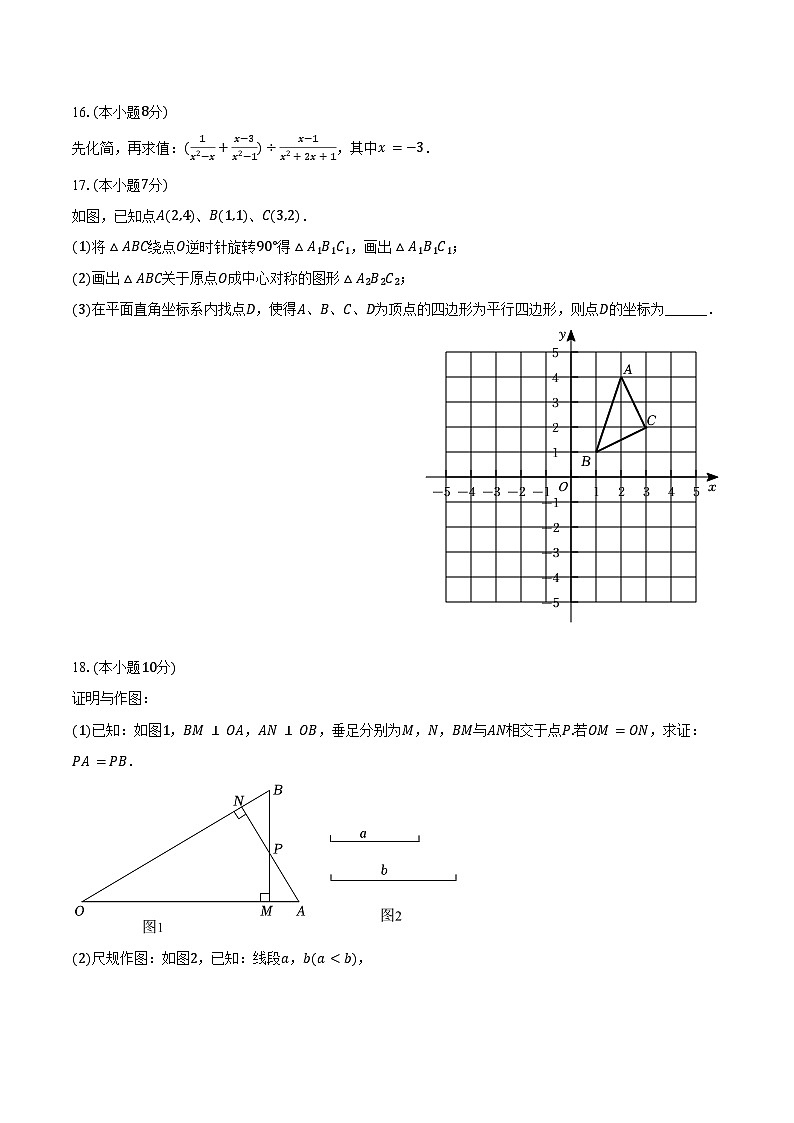
17.(本小题7分)
如图，已知点A(2,4)、B(1,1)、C(3,2)．
(1)将△ABC绕点O逆时针旋转90°得△A1B1C1，画出△A1B1C1；
(2)画出△ABC关于原点O成中心对称的图形△A2B2C2；
(3)在平面直角坐标系内找点D，使得A、B、C、D为顶点的四边形为平行四边形，则点D的坐标为______．
18.(本小题10分)
证明与作图：
(1)已知：如图1，BM⊥OA，AN⊥OB，垂足分别为M，N，BM与AN相交于点P.若OM=ON，求证：PA=PB．

(2)尺规作图：如图2，已知：线段a，b(a求作：等腰三角形ABC，使底边BC上的高为a，腰长为b.(提示：作图要保留作图痕迹，且要用2B铅笔，不用写作法)．
19.(本小题8分)
新定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“关联方程”，例如：方程x−1=3的解为x=4，而不等式组x−1>1x−2<3的解集为21x−2<3的“关联方程”．
(1)在方程①3(x+1)−x=9；②4x−7=0；③x−12+1=x中，不等式组2x−2>x−13(x−2)−x≤4的“关联方程”是______；(填序号)
(2)若关于x的方程2x−k=6是不等式组3x+12≥xx−12≥2x+13−2的“关联方程”，求k的取值范围？
20.(本小题7分)
如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使BF=BE，连接EC并延长，使CG=CE，连接FG.H为FG的中点，连接DH.求证：四边形AFHD为平行四边形．
21.(本小题10分)
某公司积极响应节能减排号召，决定采购新能源A型和B型两款汽车，已知每辆A型汽车的进价是每辆B型汽车的进价的1.5倍，且用3000万元购进A型汽车的数量比用2400万元购进B型汽车的数量少20辆，该公司决定用不多于3600万元购进A型和B型汽车共150辆，最多可以购买多少辆A型汽车？
22.(本小题12分)
阅读材料：教材中把形如a2±2ab+b2的式子叫做完全平方式.如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法.利用配方法不仅可以将多项式进行因式分解，还能解决求一些多项式最大值或最小值等问题.例如：
①分解因式：x2+2x−3：
x2+2x−3=(x2+2x+1)−3−1=(x+1)2−4=(x+1+2)(x+1−2)=(x+3)(x−1)．
②求多项式2x2+4x−3的最小值：
2x2+4x−3=2(x2+2x)−3=2(x2+2x+1)−3−2=2(x+1)2−5．
∵2(x+1)2≥0，∴2(x+1)2−5≥−5，
∴当x=−1时，2x2+4x−3有最小值，最小值是−5．
解决问题：(1)若多项式x2+kx+49是完全平方式，则常数k的值为______；
(2)分解因式：x2−4x−5；
(3)当x为何值时，多项式−3x2+6x+5有最大值？并求出这个最大值．
拓展应用：
(4)若实数a，b满足a2−5a−b+7=0，则多项式a+b的最小值为______．
23.(本小题13分)
发现结论：

(1)在△ABC中，∠C=90°，∠A=30°，若设BC=a，则AC= ______；(用含有a的代数式表示)
(2)如图1，在▱ABCD中，AC是对角线，将△ABC沿AC翻折至△AB′C，CB′与边AD相交于点E，连接B′D，则△AEC的形状是______，线段B′E和DE的数量关系是______．
结论应用：
在▱ABCD中，AB≠BC，∠B=30°，AC是对角线，将△ABC沿AC翻折至△AB′C，连接B′D．
(3)如图②，已知AB=4 3，BC=2，AB′与边CD相交于点E，求△ACE的面积；
(4)已知AB=4 3，当△B′AD是以B′D为斜边的直角三角形时，求BC的长．
参考答案
1.B
2.A
3.C
4.D
5.B
6.C
7.D
8.C
9.D
10.D
11.x≠−2
12.(a+b)2(a−b)2
13.12
14.10
15.①③④
16.解：原式=[1x(x−1)+x−3(x+1)(x−1)]⋅(x+1)2x−1
=[x+1x(x−1)(x+1)+x(x−3)x(x+1)(x−1)]⋅(x+1)2x−1
=(x−1)2x(x−1)(x+1)⋅(x+1)2x−1
=x+1x，
当x=−3时，原式=−3+1−3=23．
17.(1)如图，△A1B1C1即为所求，点C1的坐标为(−2,3)．
(2)△A2B2C2即为所求，点A2的坐标为(−2,−4)
(3)如图，满足条件的点D的坐标为(4,5)或(0,3)或(2,−1)．
18.(1)证明：∵BM⊥AO，AN⊥OB，
∴∠OMB=∠ONA=90°，
在△OMB和△ONA中，
∠OMB=∠ONAOM=ON∠O=∠O，
∴△OMB≌△ONA(ASA)，
∴OB=OA，
∵OM=ON，
∴AM=BN，
在△PMA和△PNB中，
∠APM=∠BPN∠AMP=∠BNP=90°AM=BN，
∴△PMA≌△PNA(AAS)，
∴PA=PB；
(2)解：如图，△ABC即为所求．

19.解：(1)①②；
(2)3x+12≥x①x−12≥2x+13−2②，
解不等式①得：x≥−1，
解不等式②得：x≤7，
∴原不等式组的解集为：−1≤x≤7，
∵2x−k=6，
∴2x=6+k，
∴x=6+k2，
∵关于x的方程2x−k=6是不等式组3x+12≥xx−12≥2x+13−2的“关联方程”，
∴−1≤6+k2≤7，
解得：−8≤k≤8，
∴k的取值范围为：−8≤k≤8．
20.证明：∵四边形ABCD为平行四边形，
∴AD//BC，AD=BC，
∵BF=BE，CG=CE，
∴BC为△EFG的中位线，
∴BC//FG，BC=12FG，
又∵H为FG的中点，
∴FH=12FG，
∴FH//AD，FH=AD，
∴四边形AFHD为平行四边形．
21.解：设B型汽车的进价为每辆x万元，则A型汽车的进价为每辆1.5x万元，
由题意得：2400x−30001.5x=20，
解得：x=20，
经检验，x=20是原方程的解，且符合题意，
∴1.5x=1.5×20=30，
∴A型汽车的进价为每辆30万元，B型汽车的进价为每辆20万元，
设购买m辆A型汽车，则购买(150−m)辆B型汽车，
由题意得：30m+20(150−m)≤3600，
解得：m≤60，
答：最多可以购买60辆A型汽车．
22.(1)±14；
(2)x2−4x−5=x2−4x+4−9=(x−2)2−9=(x−5)(x+1)；
(3)−3x2+6x+5=−3(x2−2x)+5=−3(x−1)2+8，
当x=1时，有最大值，最大值为8；
(4)∵a2−5a−b+7=0，
∴b=a2−5a+7，
∴a+b=a2−4a+7=(a−2)2+3，
当a=2时，有最小值，最小值为3；
23.(1)2a；
(2)等腰三角形，B′E=DE；
(3)如图2，作CG⊥AB′于G，
∵∠B=30°，BC=2，
∴∠AB′C=30°，B′C=2，
∴CG=12B′C=1，B′G= 3CG= 3，
∵AB′=AB=4 3，
∴AG=3 3，
设AE=CE=x，则EG=3 3−x，
∵CG2+EG2=CE2，
∴12+(3 3−x)2=x2，
解得x=14 39，
∴AE=14 39，
∴S△AEC=12AE⋅CG=12×14 39×1=7 39．
(4)如图2，∵AD=BC，BC=B′C，
∴AD=B′C，
∵AC//B′D，
∴四边形ACB′D是等腰梯形，
∵∠B=30°，
∴∠AB′C=∠CDA=30°，
∵△AB′D是直角三角形，
当∠B′AD=90°，AB>BC时，
设∠ADB′=∠CB′D=y，
∴∠AB′D=y−30°，
∵∠AB′D+∠ADB′=90°，
∴y−30°+y=90°，解得y=60°，
∴∠AB′D=y−30°=30°，
∵AB′=AB=4 3，
∴AD= 33×4 3=4，
∴BC=4，
当∠B′AD=90°，AB∵AD=BC，BC=B′C，
∴AD=B′C，
∵AC//B′D，∠B′AD=90°，
∴∠B′GC=90°，
∵∠B=30°，AB=4 3，
∴∠AB′C=30°，
∴GC=12B′C=12BC，
∴G是BC的中点，
在Rt△ABG中，BG= 32AB=6，
∴BC=12；
综上所述，当BC的长为4或12时，△AB′D是直角三角形．