2025高考数学一轮复习-7.3空间直线、平面的平行-专项训练【含解析】

这是一份2025高考数学一轮复习-7.3空间直线、平面的平行-专项训练【含解析】，共14页。

A. 若a//α ，b⊂α ，则a//bB. 若a//α ，b//β ，α//β ，则a//b
C. 若a⊂α ，b⊂β ，a//b，则α//βD. 若a⊄α ,b⊂α ,a//b，则a//α
2. 平面α 内两条直线m，n都平行于平面β ，则α 与β 的关系是（ ）.
A. 平行B. 相交C. 重合D. 不确定
3. 已知α ,β 是空间中两个不同的平面，命题p：“α//β ”，命题q：“平面α 内有无数条直线与β 平行”，则p是q的（ ）.
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
4. 已知a,b是两条不同的直线，α ,β 是两个不同的平面，下列结论中正确的是（ ）.
A. 若a//α ,a⊥b，则b⊥α
B. 若a⊥α ,a⊥b，则b//α
C. 若a⊂α ,b⊂α ,a//β ,b//β ，则α//β
D. 若a∩b=A,a//α ,b//α ,a//β ,b//β ，则α//β
5. （改编）已知直线a和平面α ，则a//α 的一个充分条件是（ ）.
A. 存在一条直线b，a//b且b⊂αB. 存在一条直线b，a⊥b且b⊥α
C. 存在一个平面β ，a⊂β 且α//βD. 存在一个平面β ，a//β 且α//β
6. 已知三条互相平行的直线a,b,c，α ,β 为两个不同的平面，a⊂α ,b⊂β ,c⊂β ，则两个平面α ，β 的位置关系是（ ）.
A. 平行B. 相交C. 垂直D. 平行或相交
7. 如图，四边形ABDC是梯形，AB//CD，且AB//平面α ，M是AC的中点，且AC与平面α 交于点M,BD与平面α 交于点N，AB=4，CD=6，则MN=（ ）.
A. 4.5B. 5C. 5.4D. 5.5
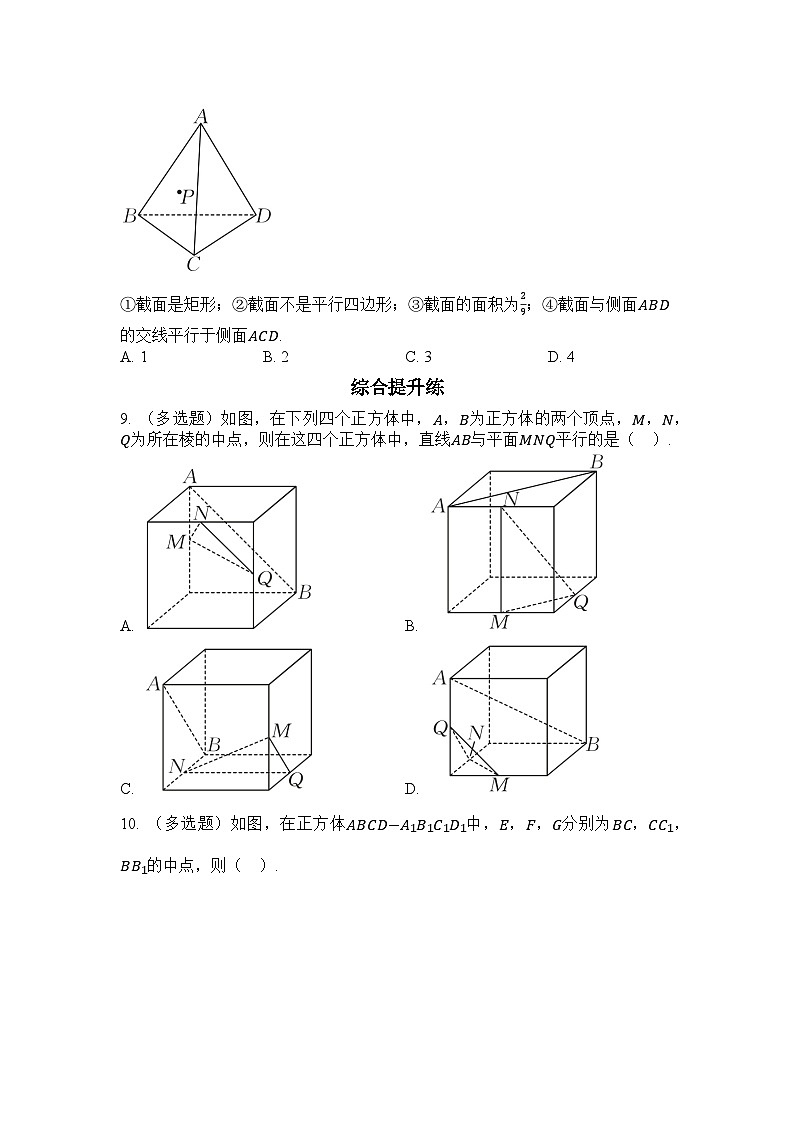
8. 如图,这是棱长为1的正四面体形状的木块，点P是△ABC的中心，过点P将木块锯开，并使得截面平行于AD和BC，则下列关于截面的说法正确的个数为（ ）.
①截面是矩形；②截面不是平行四边形；③截面的面积为29；④截面与侧面ABD的交线平行于侧面ACD.
A. 1B. 2C. 3D. 4
综合提升练
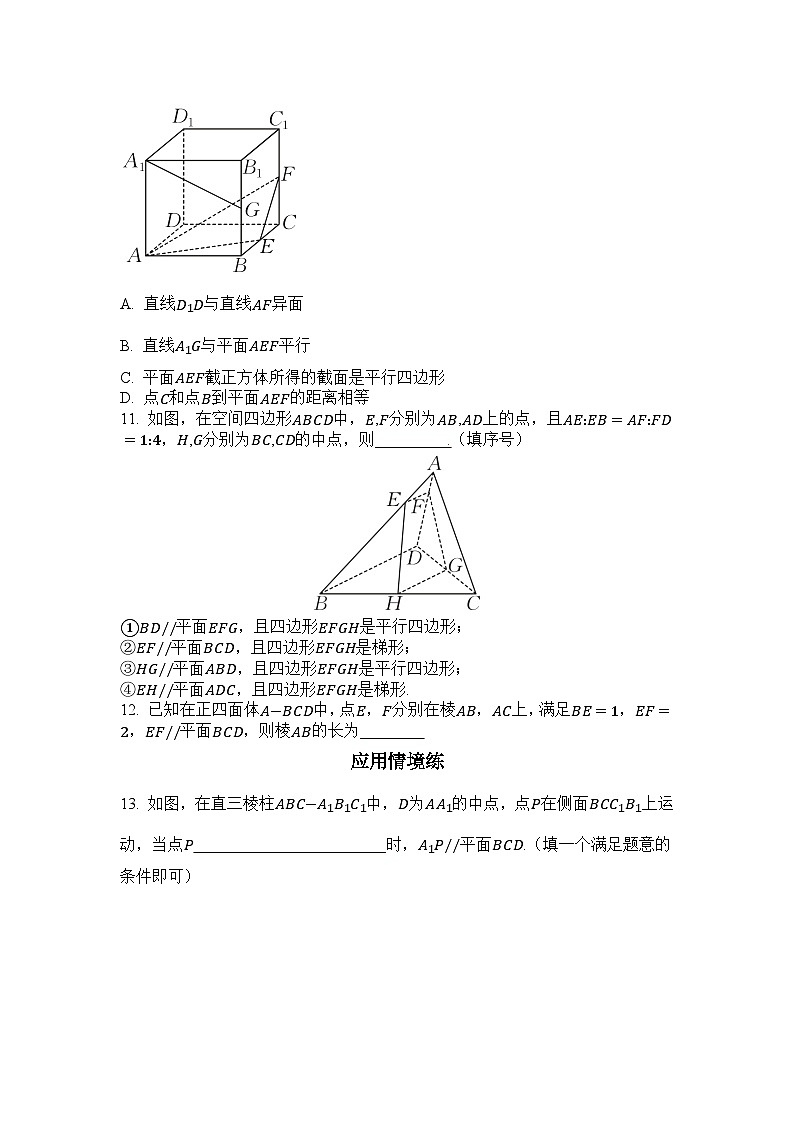
9. （多选题）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ平行的是（ ）.
A. B.
C. D.
10. （多选题）如图，在正方体ABCD−A1B1C1D1中，E，F，G分别为BC，CC1，BB1的中点，则（ ）.
A. 直线D1D与直线AF异面
B. 直线A1G与平面AEF平行
C. 平面AEF截正方体所得的截面是平行四边形
D. 点C和点B到平面AEF的距离相等
11. 如图，在空间四边形ABCD中，E,F分别为AB,AD上的点，且AE:EB=AF:FD=1:4，H,G分别为BC,CD的中点，则_________.（填序号）
①BD//平面EFG，且四边形EFGH是平行四边形；
②EF//平面BCD，且四边形EFGH是梯形；
③HG//平面ABD，且四边形EFGH是平行四边形；
④EH//平面ADC，且四边形EFGH是梯形.
12. 已知在正四面体A−BCD中，点E，F分别在棱AB，AC上，满足BE=1，EF=2，EF//平面BCD，则棱AB的长为________
应用情境练
13. 如图，在直三棱柱ABC−A1B1C1中，D为AA1的中点，点P在侧面BCC1B1上运动，当点P________________________时，A1P//平面BCD.（填一个满足题意的条件即可）
．
14. 如图，AB是圆O的直径，C是圆O上异于A,B的点，直线PC⊥ 平面ABC，E,F分别是PA，PC的中点.记平面BEF与平面ABC的交线为l，求证：直线l//平面PAC.
创新拓展练
15. 已知在长方体ABCD−A1B1C1D1中，BC=CC1=6，AB=2，平面α 过棱AB，BC，CC1的中点，点M∈ 底面ABCD.若直线MD1∩ 平面α=⌀ ，则B1M的最小值为________
16. 已知正方体ABCD−A1B1C1D1的棱长为2，E为CD的中点，且点P在四边形BCC1B1内部及其边界上运动.若总是保持EP//平面BDD1B1，求动点P的轨迹长度.
7.3空间直线、平面的平行-专项训练【解析版】
基础巩固练
1. 设a,b为两条直线，α ,β 为两个平面，下列说法中正确的是（ D ）.
A. 若a//α ，b⊂α ，则a//bB. 若a//α ，b//β ，α//β ，则a//b
C. 若a⊂α ，b⊂β ，a//b，则α//βD. 若a⊄α ,b⊂α ,a//b，则a//α
[解析]对于A，如图1，满足a//α ，b⊂α ，但a,b不平行，A错误；
对于B，如图2，满足a//α ，b//β ，α//β ，但a,b不平行，B错误；
对于C，如图3，满足a⊂α ，b⊂β ，a//b，但α ,β 不平行，C错误；
对于D，若a⊄α ,b⊂α ,a//b，由线面平行的判定定理可得a//α ，D正确.故选D.
2. 平面α 内两条直线m，n都平行于平面β ，则α 与β 的关系是（ D ）.
A. 平行B. 相交C. 重合D. 不确定
[解析]若直线m 与直线n 为相交直线，根据平面与平面平行的判定定理可得α//β ；
若m//n，如图，可能α//β ，也可能α 与β 相交.故选D.
3. 已知α ,β 是空间中两个不同的平面，命题p：“α//β ”，命题q：“平面α 内有无数条直线与β 平行”，则p是q的（ A ）.
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
[解析]若α//β ，则平面α 内的任意一条直线平行于平面β ，故平面α 内有无数条直线与β 平行，所以p 可以推出q.根据面面平行的判定定理，如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行.若平面α 内有无数条直线与β 平行，则α 与β 可能相交，不一定平行，所以q 不能推出p.故选A.
4. 已知a,b是两条不同的直线，α ,β 是两个不同的平面，下列结论中正确的是（ D ）.
A. 若a//α ,a⊥b，则b⊥α
B. 若a⊥α ,a⊥b，则b//α
C. 若a⊂α ,b⊂α ,a//β ,b//β ，则α//β
D. 若a∩b=A,a//α ,b//α ,a//β ,b//β ，则α//β
[解析]已知a,b是两条不同的直线，α ,β 是两个不同的平面，若a//α ,a⊥b，则b 与α 可能相交、平行或b⊂α ，故A 错误；若a⊥α ,a⊥b，则b//α 或b⊂α ，故B 错误；若a⊂α ,b⊂α ,a//β ,b//β ，则α//β 或α ,β 相交，故C 错误；若a∩b=A，则a,b确定一个平面，设为γ ，又a//α ,b//α ,a//β ,b//β ，则由面面平行的判定定理得γ//α ,γ//β ，所以α//β ，故D 正确.故选D.
5. （改编）已知直线a和平面α ，则a//α 的一个充分条件是（ C ）.
A. 存在一条直线b，a//b且b⊂αB. 存在一条直线b，a⊥b且b⊥α
C. 存在一个平面β ，a⊂β 且α//βD. 存在一个平面β ，a//β 且α//β
[解析]A，B，D中，均有可能a⊂α ，故A,B,D错误；C中，两平面平行，则其中一个平面内的任一条直线都平行于另一平面.故选C.
6. 已知三条互相平行的直线a,b,c，α ,β 为两个不同的平面，a⊂α ,b⊂β ,c⊂β ，则两个平面α ，β 的位置关系是（ D ）.
A. 平行B. 相交C. 垂直D. 平行或相交
[解析]如图，
由题意易得α ,β 可能平行，也可能相交.故选D.
7. 如图，四边形ABDC是梯形，AB//CD，且AB//平面α ，M是AC的中点，且AC与平面α 交于点M,BD与平面α 交于点N，AB=4，CD=6，则MN=（ B ）.
A. 4.5B. 5C. 5.4D. 5.5
[解析]因为AB// 平面α ，AB⊂ 平面ABDC，平面ABDC∩ 平面α=MN，所以AB//MN.又M 是AC 的中点，所以MN 是梯形ABDC 的中位线，故MN=12AB+CD=5.故选B.
8. 如图,这是棱长为1的正四面体形状的木块，点P是△ABC的中心，过点P将木块锯开，并使得截面平行于AD和BC，则下列关于截面的说法正确的个数为（ C ）.
①截面是矩形；②截面不是平行四边形；③截面的面积为29；④截面与侧面ABD的交线平行于侧面ACD.
A. 1B. 2C. 3D. 4
[解析]由题意可知，点P 是△ABC 的中心，如图，过点P 作EF//BC,分别交AB,AC于点E,点F，作FG//AD 交CD 于点G，
设平面EFG 与BD 交于点H，
由于BC⊄ 平面EFG，EF⊂ 平面EFG，故BC// 平面EFG，同理AD// 平面EFG，即四边形EFGH 为截面，
因为BC// 平面EFG，平面EFG∩ 平面BCD=HG，BC⊂ 平面BCD，所以BC//HG，所以EF//HG,同理FG//EH，所以四边形EFGH 为平行四边形，即截面是平行四边形，②错误；
设M 为BC 的中点，连接AM,DM，
则AM⊥BC,DM⊥BC，AM,DM⊂ 平面ADM，所以BC⊥ 平面ADM，
又AD⊂ 平面ADM，所以BC⊥AD，所以EF⊥FG，即平行四边形EFGH 为矩形，即截面是矩形，①正确；
因为点P 是△ABC 的中心，所以AP=23AM，
所以EF=23BC=23,AF=23AC,所以FG=13AD=13，故矩形EFGH 的面积为EF⋅FG=29,即截面的面积为29，③正确；
由于截面与侧面ABD 的交线为EH，且EH//FG,FG⊂ 平面ACD,EH⊄ 平面ACD，故EH// 平面ACD，即截面与侧面ABD 的交线平行于侧面ACD，④正确.故选C.
综合提升练
9. （多选题）如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ平行的是（ ABC ）.
A. B.
C. D.
[解析]对于A，如图1，连接A1B1，则AB//A1B1，
因为N，Q分别为所在棱的中点，所以由三角形中位线定理可得NQ//A1B1，所以NQ//AB，因为AB⊄ 平面MNQ，NQ⊂ 平面MNQ，所以AB// 平面MNQ.
对于B，如图2,连接A1B1，
因为M，Q分别为A1C1，B1C1的中点，所以MQ//A1B1，因为AB//A1B1，所以MQ//AB，因为AB⊄ 平面MNQ，MQ⊂ 平面MNQ，所以AB// 平面MNQ.
对于C，如图3，连接A1B1，则AB//A1B1，
因为M，Q分别为所在棱的中点，所以由三角形中位线定理可得MQ//A1B1，所以MQ//AB，
因为AB⊄ 平面MNQ，MQ⊂ 平面MNQ，所以AB// 平面MNQ.
对于D，如图4,取底面中心O，连接OQ，A1B，
由于Q 为所在棱的中点，所以由三角形中位线定理可得OQ//AB，因为OQ 与平面MNQ 相交，所以直线AB 与平面MNQ 相交.故选ABC.
10. （多选题）如图，在正方体ABCD−A1B1C1D1中，E，F，G分别为BC，CC1，BB1的中点，则（ ABD ）.
A. 直线D1D与直线AF异面
B. 直线A1G与平面AEF平行
C. 平面AEF截正方体所得的截面是平行四边形
D. 点C和点B到平面AEF的距离相等
[解析]对于A，由图可知,AF与DD1 显然不平行，且不相交，所以AF 与DD1 异面，故A 正确；
对于B，取B1C1 的中点M，连接A1M，GM，如图1所示,
图1
易知A1M//AE，且A1M⊄ 平面AEF，AE⊂ 平面AEF，
所以A1M// 平面AEF，
又易知GM//EF，
因为GM⊄ 平面AEF，EF⊂ 平面AEF，
所以GM// 平面AEF，
又A1M∩GM=M，所以平面A1MG// 平面AEF，
又A1G⊂ 平面A1MG，所以A1G// 平面AEF，故B 正确；
对于C，连接AD1，D1F，如图2所示,
图2
易知AD1//EF，所以平面AEF 截正方体所得的截面为等腰梯形AEFD1，故C 错误；
对于D，平面AEF 过BC 的中点E，即平面AEF 将线段BC 平分，
所以点C 与点B 到平面AEF 的距离相等，故D 正确.故选ABD.
11. 如图，在空间四边形ABCD中，E,F分别为AB,AD上的点，且AE:EB=AF:FD=1:4，H,G分别为BC,CD的中点，则②.（填序号）
①BD//平面EFG，且四边形EFGH是平行四边形；
②EF//平面BCD，且四边形EFGH是梯形；
③HG//平面ABD，且四边形EFGH是平行四边形；
④EH//平面ADC，且四边形EFGH是梯形.
[解析]因为E，F分别为AB，AD上的点，且AE:EB=AF:FD=1:4，
所以EF//BD，EF=15BD.
因为H，G分别为BC，CD的中点，
所以GH//BD，GH=12BD，
所以EF//GH，EF≠GH，
所以四边形EFGH 为梯形.
因为EF//BD，EF⊄ 平面BCD，BD⊂ 平面BCD，
所以EF// 平面BCD，
若EH// 平面ADC，则由线面平行的性质可得EH//FG，
又EH 与FG 不平行，
所以EH 与平面ADC 不平行.
12. 已知在正四面体A−BCD中，点E，F分别在棱AB，AC上，满足BE=1，EF=2，EF//平面BCD，则棱AB的长为3.
[解析]因为EF// 平面BCD，EF⊂ 平面ABC,平面ABC∩ 平面BCD=BC，所以EF//BC,
因为正四面体A−BCD 的每个面都是等边三角形，所以△AEF 也为等边三角形，所以AB=BE+AE=BE+EF=1+2=3.
应用情境练
13. 如图，在直三棱柱ABC−A1B1C1中，D为AA1的中点，点P在侧面BCC1B1上运动，当点P在CC1 的中点F 与BB1 的中点E 的连线线段上时，A1P//平面BCD.（填一个满足题意的条件即可）
[解析]设CC1 与BB1 的中点分别为F,E，则EF//BC，A1F//CD，∵EF⊄ 平面BCD，BC⊂ 平面BCD,∴EF//平面BCD.同理，A1F//平面BCD.又EF,A1F⊂ 平面A1EF,且EF∩A1F=F,∴ 平面A1EF// 平面BCD，故线段EF 上的任意一点与A1 的连线都平行于平面BCD．
14. 如图，AB是圆O的直径，C是圆O上异于A,B的点，直线PC⊥ 平面ABC，E,F分别是PA，PC的中点.记平面BEF与平面ABC的交线为l，求证：直线l//平面PAC.
[解析]因为E，F分别是PA,PC的中点，所以EF//AC.
因为AC⊂ 平面ABC，EF⊄ 平面ABC，所以EF// 平面ABC.
又EF⊂ 平面BEF，平面BEF 与平面ABC 的交线为l，所以EF//l.
又l⊄ 平面PAC，EF⊂ 平面PAC，所以直线l// 平面PAC.
创新拓展练
15. 已知在长方体ABCD−A1B1C1D1中，BC=CC1=6，AB=2，平面α 过棱AB，BC，CC1的中点，点M∈ 底面ABCD.若直线MD1∩ 平面α=⌀ ，则B1M的最小值为31105 .
[解析]记棱AB，BC，CC1的中点分别为E，F，G，连接EF，FG，EG，BC1，AD1，AC，CD1，如图所示,
则平面α 即平面EFG.
因为FG//BC1，BC1//AD1，
所以AD1//FG，且AD1⊄ 平面EFG，FG⊂ 平面EFG，
所以AD1// 平面EFG.
同理可得，AC//平面EFG.
又AD1∩AC=A，
所以平面D1AC// 平面EFG，故点M 在线段AC 上.
而B1M=BB12+BM2=36+BM2，
所以只需BM 最小即可，
BM 的最小值为点B 到线段AC 的距离2×622+62=3105，
故B1M 的最小值为36+31052=31105.
16. 已知正方体ABCD−A1B1C1D1的棱长为2，E为CD的中点，且点P在四边形BCC1B1内部及其边界上运动.若总是保持EP//平面BDD1B1，求动点P的轨迹长度.
[解析]如图，分别取BC,B1C1的中点F,G，连接EF,FG,EG，则BF=12BC,B1G=12B1C1，因为BC//B1C1，BC=B1C1，所以BF//B1G，BF=B1G，
所以四边形BFGB1 为平行四边形，所以BB1//FG，
又因为E 为CD 的中点，所以EF//BD，
因为EF⊄ 平面BDD1B1,FG⊄ 平面BDD1B1，BD⊂ 平面BDD1B1,BB1⊂ 平面BDD1B1，所以EF// 平面BDD1B1，FG//平面BDD1B1，
因为EF∩FG=F，所以平面EFG// 平面BDD1B1，
因为平面EFG∩ 平面BCC1B1=FG，点P 在四边形BCC1B1 内部及其边界上运动，EP//平面BDD1B1，
所以点P 的轨迹是线段FG，
因为FG=BB1=2，所以动点P 的轨迹长度为2.