

人教版九年级数学上册同步讲义专题第10课 二次函数y=ax2与y=a(x-h)2+k的图像与性质(学生版)
展开知识精讲
知识点01 二次函数y=ax2的图象和性质
1、二次函数y=ax2的图象的画法
【示例】在同一平面直角坐标系中作出和的图象.
解:列表如下
描点:如图所示,以表中各组对应值为点的坐标,在平面直角坐标系内描出相应的点.
连线:用光滑的曲线顺次连接各点.
【方法总结】
画二次函数y=ax2的图象的三点注意
(1)列表时,自变量应以О为中心,左右两边要对应取值;
(2)画图象时,图象应越过端点,表示为向下或向上无限延伸﹔
(3)图象在两个象限内画出的曲线是对称的,顶点处不能画成尖形,应该保持平滑.
2、二次函数y=ax2的图象和性质
【注意】
(1)二次函数y =ax2的增减性一定要说明是在y轴的左侧或右侧.不能笼统地说当a>0时,y随x的增大而减小(增大).
(2)|a|决定抛物线y=ax2开口 ,|a|越大,抛物线开口越 .
知识点02 二次函数y=a(x—h)2十k的图象和性质
1、二次函数 的图象的画法
(1)描点法
(2)平移法
【注意】
(1)抛物线y=ax2+k 是由抛物线y=ax2上下平移得到的.当k>0时,上移;当k<0时,下移,简记为“ ”.
(2)抛物线y=a(a-h)2是由抛物线y=ax2左右平移得到的.当h>0时,右移;当h<0时,左移,简记为“ ”.
(3)对于二次项系数a相同的两个二次函数,它们对应的抛物线的开口方向和大小是一样的,此时可以只通过观察顶点的位置来判断抛物线的平移情况,也可以利用“左加右减,上加下减”的规律来判断.
【示例】
在同一平面直角坐标系中,画出 的图象,并指出后三个图象与的图象之间的关系.
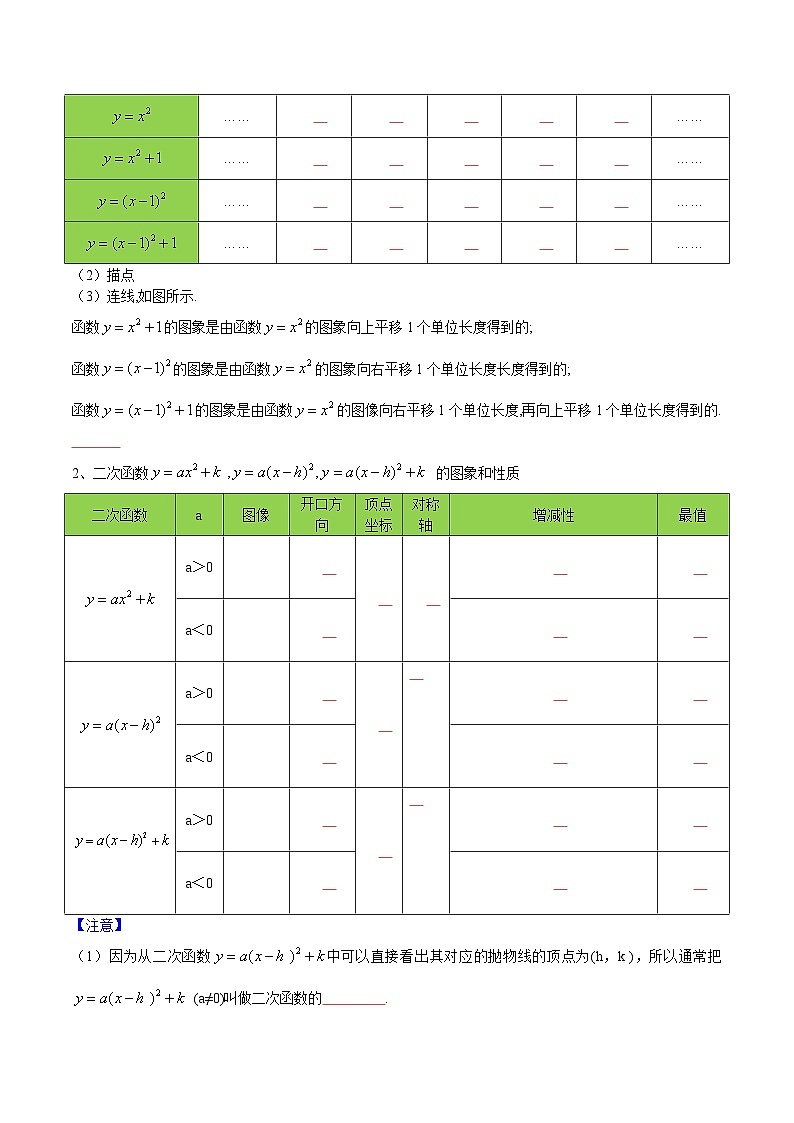
解:(1)列表如下:
(2)描点
(3)连线,如图所示.
函数的图象是由函数的图象向上平移1个单位长度得到的;
函数的图象是由函数的图象向右平移1个单位长度长度得到的;
函数的图象是由函数的图像向右平移1个单位长度,再向上平移1个单位长度得到的.
2、二次函数 的图象和性质
【注意】
(1)因为从二次函数中可以直接看出其对应的抛物线的顶点为(h,k ),所以通常把 (a≠0)叫做二次函数的 .
(2)抛物线(a=0)与x轴可能有交点,也可能没有交点,但与y轴一定有 个交点.
考法01 二次函数y=ax2的图象和性质
【例题1】已知函数,不画图象,回答下列各题:
(1)其图象的开口方向:
(2)其图象的对称轴:
(3)其图象的顶点坐标:
(4)当x>0时,y随x的增大而 ;
(5)当x__时,函数y的最 值是
【方法总结】
已知二次函数y=ax2的解析式,函数的性质实际上已经确定了,如果你记不准这么多性质结论,不妨画个草图,它能帮你快速准确地找到问题的答案.
考法02 的图象和性质
【例题2】说出下列抛物线的开口方向、对称轴和顶点坐标.
【方法总结】
抛物线的各种形式
抛物线有多种形式,比如当h=0,k=0时,变为y=ax2+k ;
当h=0,k=0 时,变为y=a(x-h)2.解决各种形式的抛物线的性质问题的关键是要记准抛物线的开口方向、对称轴和顶点坐标.
考法03 二次函数y=a(x-h)2+k的图象特征和性质
【例题3】二次函数:
(1)以上二次函数的图象的对称轴为直线x=-1的是 (只填序号);
(2)以上二次函数有最大值的是 (只填序号)﹔
(3)以上二次函数的图象中关于x轴对称的是 (只填序号).
【方法总结】
由二次函数的顶点式推断抛物线性质的方法
(1)a确定抛物线的开口方向,且|a|的大小决定开口的大小,特别地,当两个抛物线形状一样时,两者的|a |是相等的;
(2)h确定抛物线的对称轴,对称轴是直线x=h,千万不要记成x=-h ;
(3)k确定抛物线与对称轴交点的纵坐标.h与k 共同确定抛物线的顶点坐标(h ,k).
考法04 根据二次函数图象的平移规律,确定二次函数的解析式
【例题4】将抛物线先向下平移2个单位长度,再向右平移3个单位长度后所得抛物线对应的二次函数解析式为
【方法总结】
根据平移规律,确定二次函数解析式的策略抛物线在平移时,a不变,只是h和
k 发生变化.因此,在解决抛物线平移问题时,可按照“上加下减”“左加右减”的平移规律,确定平移后抛物线对应的二次函数解析式.
考法05 比较函数值的大小
【例题5】已知点A(4,y1),B(,y2),C(-2,y3)都在二次函数的图象上,则y1,y2,y3的大小关系是
【方法总结】
比较二次函数中函数值大小的三种常用方法
(1)直接代入自变量的值,求得函数值后比较大小.
(2)当自变量的取值在对称轴同侧时,直接根据二次函数的增减性判断.
(3)当自变量的取值在对称轴两侧时,根据自变量的取值到对称轴的距离及二次函数的增减性判断.
考法06 根据二次函数的增减性求字母的取值范围
【例题6】若二次函数,当x<2时,y随x的增大而减小,则m的取值范围是( )
A.m=2B.m>2C.m≥2D.m2
【方法总结】
根据二次函数的增减性求字母的取值范围的步骤
第1步:根据二次函数的顶点式,确定抛物线的开口方向和对称轴.
第2步:明确函数在对称轴两侧的增减情况.
第3步:借助图象或性质确定字母的取值范围.
考法07 用顶点式y=a(x-h )2+k求二次函数的解析式
【例题7】已知抛物线的顶点坐标为A(2,1),且抛物线过点B(3,0),求抛物线对应的函数解析式.
考法08 二次函数y=ax2与一次函数的综合性问题
【例题8】如图,直线l过A(3,0)和 B(0,3)两点,它与二次函数的图象在第一象限内交于点P,若△AOP的面积为3,求该二次函数的解析式.
考法09 利用二次函数的图象和性质解决实际问题
【例题9】如图 (示意图),一位运动员在距篮下4 m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5 m时,达到最大高度3.5 m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05 m.
(1)建立如图所示的平面直角坐标系,求抛物线对应的函数解析式;
(2)该运动员身高1.8 m,在这次跳投中,球在头顶上方0.25 m处出手,问:球出手时,他跳离地面的高度是多少?
题组A 基础过关练
1.抛物线y=-(x-1)2-2的顶点坐标是( )
A.(-1,2)B.(-1,-2)C.(1,-2)D.(1,2)
2.抛物线顶点坐标是
A.B.
C.D.
3.抛物线y=-3(x+1)2不经过的象限是( )
A.第一、二象限B.第二、四象限C.第三、四象限D.第二、三象限
4.要得到抛物线,可以将抛物线( )
A.向左平移2个单位长度,再向上平移3个单位长度
B.向左平移2个单位长度,再向下平移3个单位长度
C.向右平移2个单位长度,再向上平移3个单位长度
D.向右平移2个单位长度,再向下平移3个单位长度.
5.二次函数的最小值是( ).
A.B.C.D.
6.二次函数的对称轴是( )
A.B.C.D.
7.二次函数y=2+3的图象是一条抛物线,则下列说法错误的是( )
A.抛物线开口向上B.抛物线的对称轴是直线x=1
C.抛物线的顶点是(1,3)D.当x>1时,y随x的增大而减小
8.关于抛物线y=﹣2(x﹣1)2说法正确的是( )
A.顶点坐标为(﹣2,1)
B.当x<1时,y随x的增大而增大
C.当x=0时,y有最大值1
D.抛物线的对称轴为直线x=﹣2
9.关于二次函数y=﹣(x+1)2+2的图象,下列判断正确的是( )
A.图象开口向上B.图象的对称轴是直线x=1
C.图象有最低点D.图象的顶点坐标为(﹣1,2)
10.已知A(,y1),B(1,y2),C(4,y3)三点都在二次函数y=﹣(x﹣2)2的图象上,则y1,y2,y3的大小关系为( )
A.y1<y2<y3B.y1<y3<y2C.y3<y1<y2D.y3<y2<y1
11.若二次函数的图象的顶点坐标为(2,-1),且抛物线过(0,3),则二次函数的解析式是( )
A.y=-(x-2)2-1B.y=-(x-2)2-1
C.y=(x-2)2-1D.y=(x-2)2-1
12.抛物线y=3(x-2)2的开口方向是______,顶点坐标为______,对称轴是______.当x______时,y随x的增大而增大;当x=______时,y有最______值是______,它可以由抛物线y=3x2向______平移______个单位得到.
13.已知二次函数y=(x﹣2)2+3,当x<2时,y随x的增大而_____.(填“增大”或“减小”)
14.已知A(-4,y1),B(-1,y2),C(2,y3)三点都在二次函数y=a(x+2)2+c(a>0)的图象上,则y1,y2,y3的大小关系为__________.
15.已知点A(4,y1),B(0,y2),C(-3,y3)都在二次函数y=(x-1)2-1的图象上,则y1,y2,y3的大小关系是____.
题组B 能力提升练
16.若二次函数,当时,y随x的增大而减小,则m的取值范围是( )
A.B.C.D.
17.二次函数 y=(x﹣2)2+3,当 0≤x≤5 时,y 的取值范围为( )
A.3≤y≤12B.2≤y≤12C.7≤y≤12D.3≤y≤7
18.在平面直角坐标系中,二次函数()的图象可能是( )
A.B.C.D.
19.已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值为( )
A.1或﹣5B.﹣1或5C.1或﹣3D.1或3
20.将抛物线绕顶点旋转,则旋转后的抛物线的解析式为( )
A.B.
C.D.
21.把二次函数化成的形式,则________,把此函数图象向右平移个单位后,它的顶点坐标是________.
22.已知抛物线y=﹣(x﹣2)2+3.
(1)写出抛物线的开口方向、对称轴和顶点坐标;
(2)当y随x的增大而增大时,求x的取值范围.
23.已知二次函数的图象经过点(0,0),且它的顶点坐标是(1,-2).
(1)求这个二次函数的表达式;
(2)判断点(3,5)是否在这个二次函数的图像上,并说明理由.
24.设k≠0,若函数y1=kx+3,y2=(x﹣k)2+k和y3=(x+k)2﹣k的图象与y轴依次交于A,B和C三点,设函数y2,y3的图象的顶点分别为D,E.
(1)当k=1时,请在直角坐标系中,分别画出函数y1,y2,y3的草图,并根据图象,写出你发现的两条结论;
(2)BC长与k之间是正比例函数关系吗?请作出判断,并说明理由;
(3)若△ADE的面积等于9,求y2随x的增大而减小时,x的取值范围.
25.如图,抛物线y=2(x-2)2与平行于x轴的直线交于点A,B,抛物线顶点为C,△ABC为等边三角形,求S△ABC;
26.已知函数是关于x的二次函数.
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,这时当x为何值时,y随x的增大而增大?
(3)m为何值时,函数有最大值?最大值是多少?这时当x为何值时,y随x的增大而减小?
题组C 培优拔尖练
27.某商场销售一种商品的进价为每件30元,销售过程中发现月销售量y(件)与销售单价x(元)之间的关系如图所示.
(1)根据图象直接写出y与x之间的函数关系式.
(2)设这种商品月利润为W(元),求W与x之间的函数关系式.
(3)这种商品的销售单价定为多少元时,月利润最大?最大月利润是多少?
28.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
29.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,,.问:顶部F是否会碰到水柱?请通过计算说明.
30.如图,在喷水池的中心A处竖直安装一个水管AB.水管的顶端安有一个喷水管、使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C.高度为3m.水柱落地点D离池中心A处3m.建立适当的平面直角坐标系,解答下列问题.
(1)求水柱所在抛物线的函数解析式;
(2)求水管AB的长.
课程标准
1、掌握二次函数y=ax2与y=a(x-h)2+k的图形与性质;
2、掌握二次函数y=ax2与y=a(x-h)2+k实际应用;
画图步骤
解释
列表
让x取一此代表性的值(正数、负数或0),求出对应的y值,列出表格
描点
在平面直角坐标系内,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点
连线
在平面直角坐标系内,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点
x
……
-3
-2
-1
0
1
2
3
……
……
……
……
……
函数
a
图像
开口方向
顶点坐标
对称轴
增减性
最值
x
……
-2
-1
0
1
2
……
……
……
……
……
……
……
……
……
二次函数
a
图像
开口方向
顶点
坐标
对称轴
增减性
最值
a>0
a<0
a>0
a<0
a>0
a<0
人教版九年级数学上册同步讲义专题第10课 二次函数y=ax2与y=a(x-h)2+k的图像与性质(教师版): 这是一份人教版九年级数学上册同步讲义专题第10课 二次函数y=ax2与y=a(x-h)2+k的图像与性质(教师版),共34页。试卷主要包含了二次函数y=ax2的图象的画法,二次函数y=ax2的图象和性质等内容,欢迎下载使用。
人教版九年级数学上册同步精品讲义 第10课 二次函数y=ax2与y=a(x-h)2+k的图像与性质(原卷版+解析): 这是一份人教版九年级数学上册同步精品讲义 第10课 二次函数y=ax2与y=a(x-h)2+k的图像与性质(原卷版+解析),共42页。试卷主要包含了二次函数y=ax2的图象的画法,二次函数y=ax2的图象和性质等内容,欢迎下载使用。
专题01 二次函数y=ax2、y=a(x-h)2、y=a(x-h)2+k的图象和性质-2023-2024学年苏科版九年级数学下册常考压轴题: 这是一份专题01 二次函数y=ax2、y=a(x-h)2、y=a(x-h)2+k的图象和性质-2023-2024学年苏科版九年级数学下册常考压轴题,共30页。












