数学必修 第一册4.4.1 对数函数的概念课堂教学课件ppt

这是一份数学必修 第一册4.4.1 对数函数的概念课堂教学课件ppt，共21页。PPT课件主要包含了教学目标，学科素养，知识回顾，指数函数的图像，新知探索，拓展提升，归纳总结，SumUp，课后作业等内容，欢迎下载使用。

Retrspective Knwledge
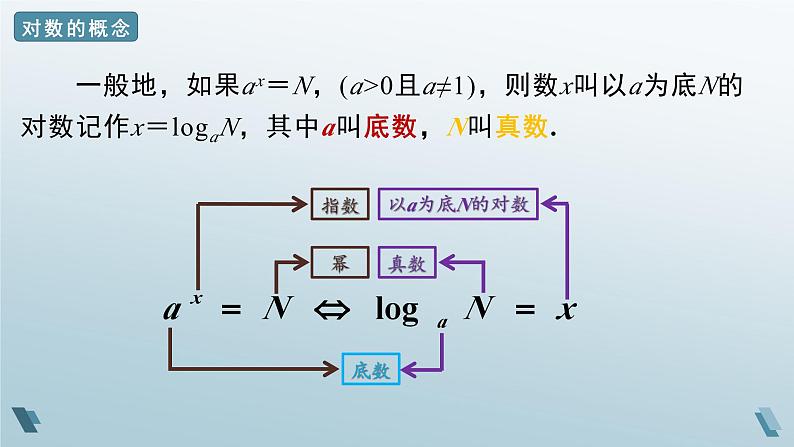
一般地，如果ax＝N，(a>0且a≠1)，则数x叫以a为底N的对数记作x＝lgaN，其中a叫底数，N叫真数.
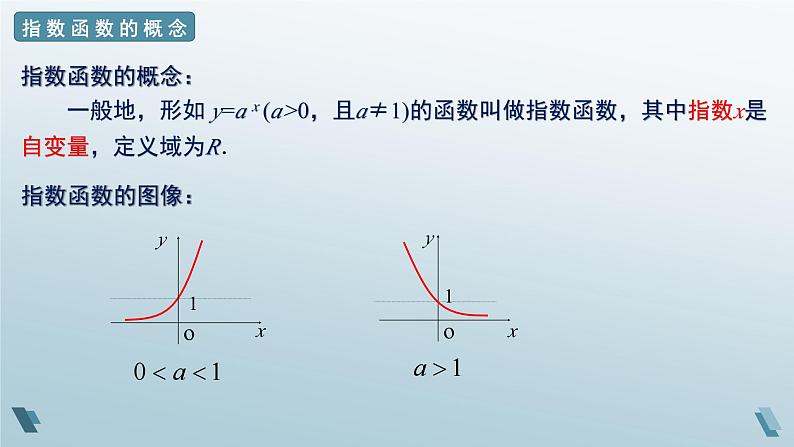
指数函数的概念： 一般地，形如 y=a x (a>0，且a≠1)的函数叫做指数函数，其中指数x是自变量，定义域为R．
New Knwledge explre
回顾问题1　当生物死亡后，它机体内原有的碳14含量会按确定的比率衰减（称为衰减率），大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”．按照上述变化规律，生物体内碳14含量y与死亡年数x之间有怎样的关系？ 设死亡生物体内碳14含量的年衰减率为p，如果把刚死亡的生物体内碳14含量看成1个单位，那么：
思考： 一般的指数函数y = ax ，(a>0,且a≠1)也能表示成x是y的函数吗？
根据指数与对数的关系：y = ax ，(a>0,且a≠1)⟺ x = lgay ,(a>0,且a≠1)
结合指数函数的图像知，上式中x与y是一一对应的，故由 x = lgay ,(a>0,且a≠1)知x也是y的函数 .
函数y = f(x)也能表示成x是y的函数的前提
通常，我们用x表示自变量，y表示函数．将x = lgay ，(a>0,且a≠1) 中的x与y对调，写成y = lgax ,(a>0,且a≠1) 的形式，我们称该函数为对数函数．
一般地，函数y = lgax ，(a>0，且a≠1) 叫做对数函数，其中x是自变量，定义域是（0，+∞）.
例1 求下列函数定义域
【解析】（1）因为 x2>0，即x ≠ 0，所以函数 y = lg3x 的定义域是 { x | x ≠ 0 } ． （2）因为4－x>0，即x < 4，所以函数 y = lga (4－x)的定义域是 { x | x < 4 } ．
例2 假设某地初始物价为1，每年以5%的增长率递增，经过y年后的物 价为x．
（1）该地的物价经过几年后会翻一番？
【解析】（1）由题意可知，经过y年后的物价x为 x=(1+5%)y即 x=1.05y，y∈[0，+∞)． 由指对数的关系可得 y = lg1.05 x，x∈[1，+∞)．
由计算工具可得，x=2当时，y≈14．所以，该地区的物价大约经过14年后会翻一番．
（2）填写下表，并根据表中的数据，说明该地物价的变化规律．
【解析】根据函数y = lg1.05 x ， x∈[1，+∞)由计算工具可得下表：
由表中的数据可以发现，该地区的物价随时间的推移在增长，物价每增加约一倍所需时间逐渐缩短.
练习1 求下列函数定义域
【解析】设 f (x) = lga x (a>0,且a≠1)． 因为函数f (x)的图象过点P(8,3)， 所以f (8)= lga 8=3， 解得a = 2， 所以 f (x) = lg2 x ． 所以
利用待定系数法.因为对数函数，指数函数，幂函数都只有一个系数，所以只需要一个点的坐标就可以求写出它们的表达式.
Expansin And Prmtin
对数函数的概念： 一般地，函数y = lgax ，(a>0，且a≠1) 叫做对数函数，其中x是自变量，定义域是（0，+∞）．
求函数的定义域依据：（1）分母不为0；（2）偶次根式内不小于0；（3）0的0次方无意义；（4）指数式和对数式的底数大于0且不等于1；（5）对数式的真数大于0．
Hmewrk After Class