

2023-2024学年北京市丰台区九年级第一学期期末数学试卷(含答案)
展开一、选择题(共16分,每题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
A
B
C
D
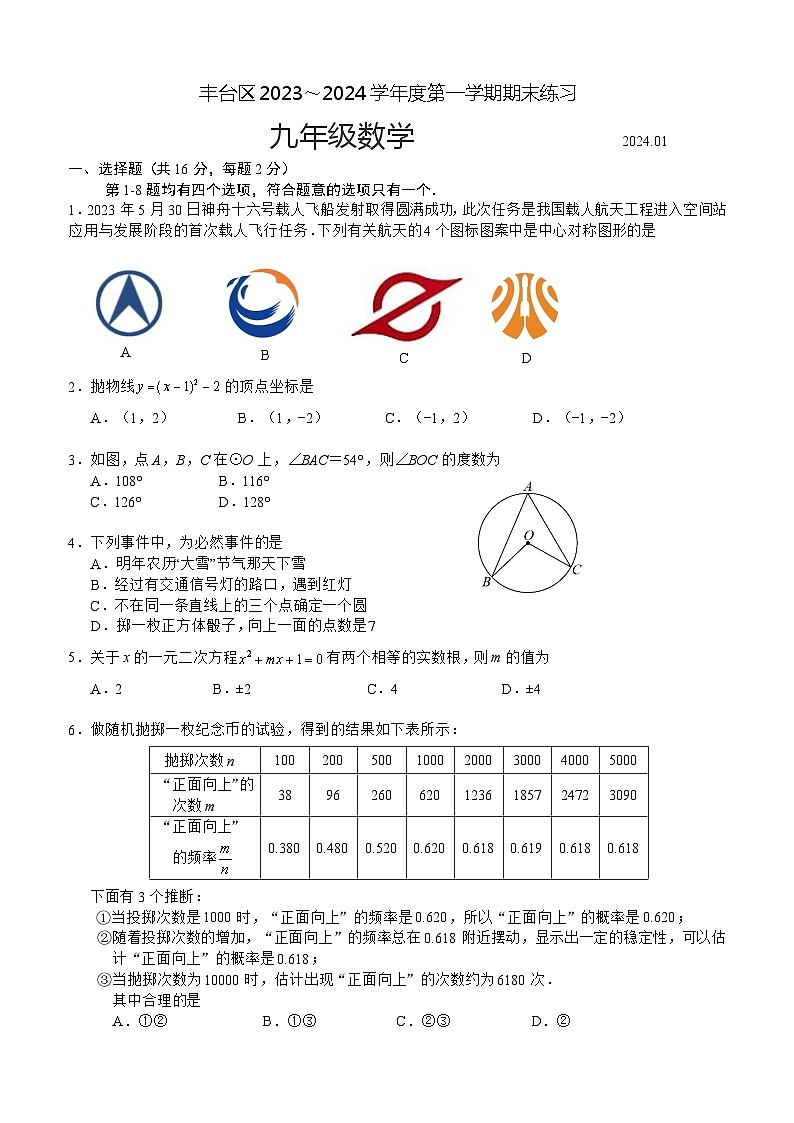
1.2023年5月30日神舟十六号载人飞船发射取得圆满成功,此次任务是我国载人航天工程进入空间站应用与发展阶段的首次载人飞行任务.下列有关航天的4个图标图案中是中心对称图形的是
2.抛物线的顶点坐标是
A.(1,2) B.(1,-2) C.(-1,2) D.(-1,-2)
3.如图,点A,B,C在⊙O上,∠BAC=54°,则∠BOC的度数为
A.108° B.116°
C.126° D.128°
4.下列事件中,为必然事件的是
A.明年农历“大雪”节气那天下雪
B.经过有交通信号灯的路口,遇到红灯
C.不在同一条直线上的三个点确定一个圆
D.掷一枚正方体骰子,向上一面的点数是7
5.关于x的一元二次方程有两个相等的实数根,则m的值为
A.2 B.±2 C.4 D.±4
6.做随机抛掷一枚纪念币的试验,得到的结果如下表所示:
下面有3个推断:
①当投掷次数是1000时,“正面向上”的频率是0.620,所以“正面向上”的概率是0.620;
②随着投掷次数的增加,“正面向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.618;
③当抛掷次数为10000时,估计出现“正面向上”的次数约为6180次.
其中合理的是
A.①② B.①③ C.②③ D.②
7.如图,点O为线段AB的中点,∠ACB=∠ADB =90°,连接OC,OD.则下面结论不一定成立的是
A.OC=OD B.∠BDC=∠BAC
C.∠BCD+∠BAD=180° D.AC平分∠BAD
8.如图,等边三角形ABC的边长为2,点A,B在⊙O上,点C在⊙O内,⊙O的半径为.将△ABC绕点A逆时针旋转,在旋转过程中得到两个结论:
①当点C第一次落在⊙O上时,旋转角为30°;
②当AC第一次与⊙O相切时,旋转角为60°.
则结论正确的是
A.① B.②
C.①② D.均不正确
二、填空题(共16分,每小题2分)
9.方程x2-x=0的解是 .
10. 一个扇形的半径是6,其圆心角是150°,则圆心角所对的弧长为 .
11.为了加快数字化城市建设,某市计划新建一批智能充电桩,第一个月新建了301个充电桩,第三个月新建了500个充电桩.设该市新建智能充电桩个数的月平均增长率为x,根据题意,列出方程是 .
12.正六边形的外接圆半径为2 cm,则此正六边形的边心距为 cm.
13.已知二次函数,当x>1时,y随x的增大而增大.写出一个满足题意的b的值为 .
14.在关于x的二次函数中,自变量x可以取任意实数,下表是自变量x与函数y的几组对应值:
根据以上信息,关于x的一元二次方程的两个实数根中,其中的一个根约等于 (结果保留小数点后一位小数).
15.如图,PA,PB分别与⊙O相切于点A,B,点C为劣弧上的点,过点C的切线分别交PA,PB于点M,N.若PA =8,则△PMN的周长为 .
16.平面直角坐标系xOy中,将抛物线在x轴和x轴下方的部分记作C1,将C1沿x轴翻折记作C2, C1和C2构成的图形记作G.关于图形G,如图所示,以下三个结论中,正确的序号是 .
①图形G关于原点对称;
②图形G关于直线y=x对称;
③图形G的面积为,满足.
三、解答题(共68分,第17-22题,每题5分,第23 -26题,每题6分,第27-28题,每题7分)
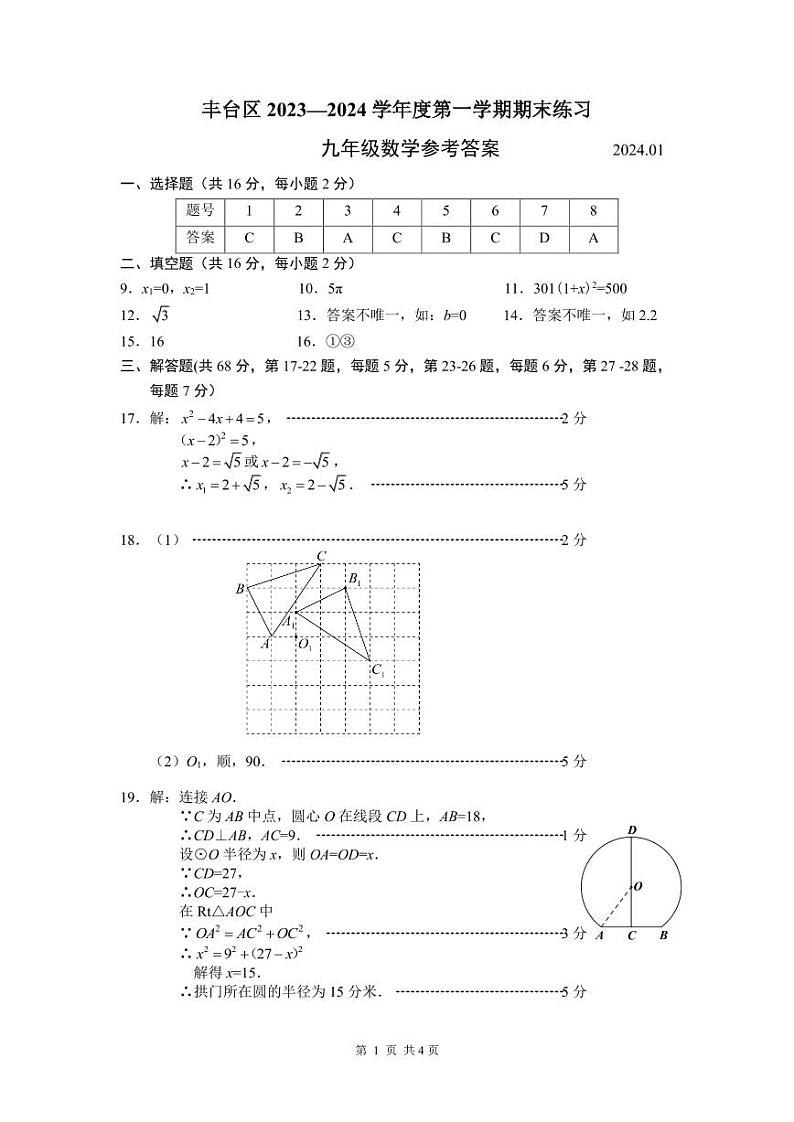
17.解方程:.
18.已知:如图,△ABC绕某点按一定方向旋转一定角度后得到△A1B1C1,点A,B,C分别对应点A1,B1,C1.
(1)在图中画出△A1B1C1;
(2)△A1B1C1是以点 (填“O1”,
“O2”或“O3” )为旋转中心,将△ABC 时针旋转 度得到的.
19.如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端AB=18分米,C为AB中点,D为拱门最高点,圆心O在线段CD上, CD=27分米,求拱门所在圆半径的长.
图1
图2
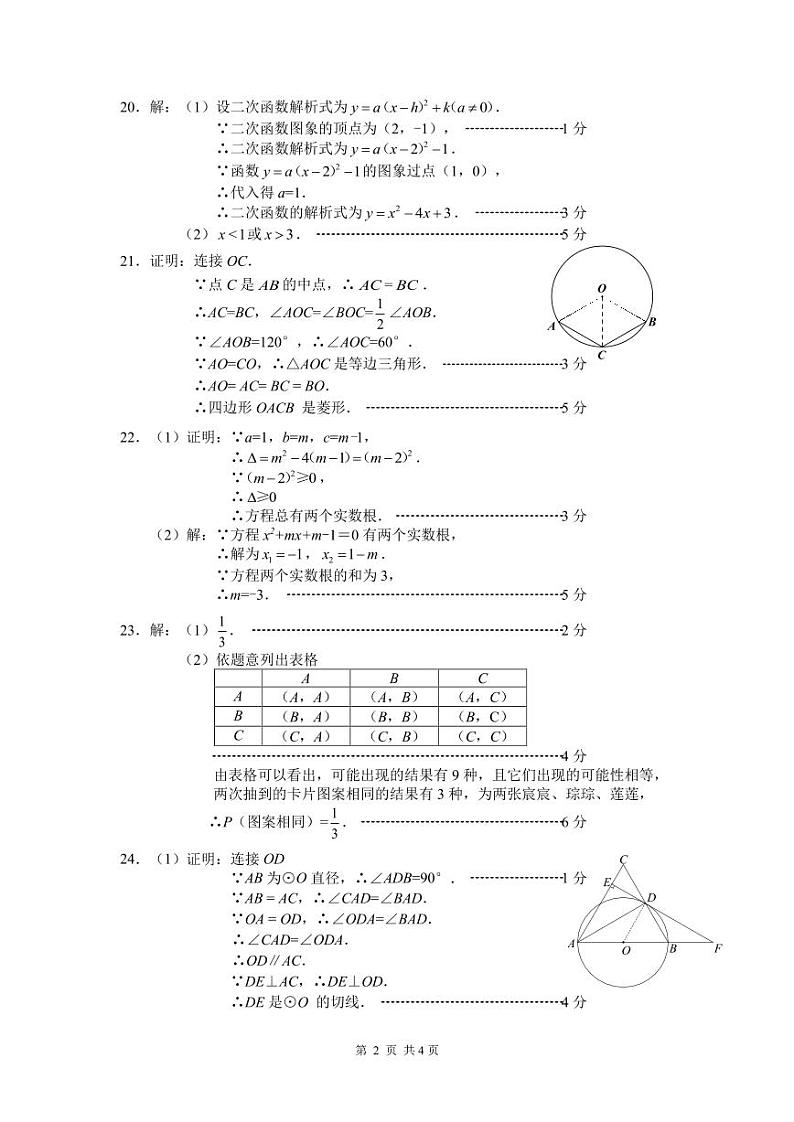
20.已知二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表所示:
(1)求二次函数的解析式及顶点坐标;
(2)直接写出当y>0时,x的取值范围.
21.如图,A,B是⊙O上的两点,∠AOB=120°,点C是的中点.
求证:四边形OACB 是菱形.
22.已知关于x的一元二次方程.
(1)求证:方程总有两个实数根;
(2)若该方程两个实数根的和为3,求m的值.
23.第19届亚运会于2023年9月在杭州成功举办,此届亚运会的吉祥物是由如图所示的三个可爱的机器人“宸宸”、“琮琮”、“莲莲”组成的.现有三张分别印有三个吉祥物的不透明卡片,三张卡片除正面图案不同外,其余均相同.
(1)从这三张卡片中随机抽取一张,图案恰好是 “宸宸”的概率为________;
(2)从这三张卡片中随机抽取一张,记住卡片图案后将卡片放回,背面朝上洗匀,然后再从三张卡片中随机抽取一张.用列表或画树状图的方法,求两次抽到的卡片图案相同的概率.(印有“宸宸”、“琮琮”、“莲莲”的三张卡片依次记为A,B,C).
24.如图,△ABC中,AB= AC,以AB为直径作⊙O交BC于点D,作DE⊥AC交AC于点E,延长ED与AB的延长线交于点F.
(1)求证:DE是⊙O 的切线;
(2)若△ABC为等边三角形,AE=3,求⊙O半径的长.
25.如图1,灌溉车为公路绿化带草坪浇水,图2是灌溉车浇水操作时的截面图.现将灌溉车喷出水的上、下边缘线近似地看作平面直角坐标系xOy中两条抛物线的部分图象.已知喷水口H离地竖直高度OH为1.2m,草坪水平宽度DE=3m,竖直高度忽略不计.上边缘抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.4m,下边缘抛物线是由上边缘抛物线向左平移4m得到,灌溉车到草坪的距离OD为d(单位:m).
(1)求上边缘抛物线的函数解析式,并求喷出水的最大射程OC的长;
(2)下边缘抛物线落地点B的坐标为 ;
(3)要使灌溉车行驶时喷出的水能浇灌到整个草坪, d的取值范围为 .
图1
图2
26.在平面直角坐标系xOy中,点(m+2,),(6,)为抛物线上两个不同的点.
(1)求抛物线的对称轴(用含m的式子表示);
(2)若 ,求m的取值范围.
27.已知在△ABC中,AB=AC,0°<∠BAC <90°,将线段AC绕点 A逆时针旋转α得到线段AD,连接BD,CD.
(1)如图1,当∠BAC=α时,∠ABD= (用含有α的式子表示);
(2)如图2,当α=90°时,连接BD,作∠BAD的角平分线交BC的延长线于点F,交BD于点E,连接DF.
①依题意在图2中补全图形,并求∠DBC的度数;
②用等式表示线段AF,CF,DF之间的数量关系,并证明.
图1
图2
28.在平面直角坐标系xOy中,⊙O的半径为1,对于线段AB和x轴上的点P,给出如下定义:将线段AB绕点P旋转180°可以得到⊙O的弦(,分别为,的对应点),则称线段AB为⊙O以点P为中心的“关联线段”.
(1)如图,已知点A(-2,-1),B(-2,0),C(-2,1),D(-1,1),在线段AC,BD,CD中,⊙O以点P为中心的“关联线段”是 ;
(2)已知点E(-4,1),线段EF是⊙O以点P为中心的“关联线段”,求点F的横坐标的取值范围;
(3)已知点E(m,1),若直线y=-x+2m上存在点F,使得线段EF是⊙O以点P为中心的“关联线段”,直接写出m的取值范围.
备用图
抛掷次数n
100
200
500
1000
2000
3000
4000
5000
“正面向上”的次数m
38
96
260
620
1236
1857
2472
3090
“正面向上”
的频率
0.380
0.480
0.520
0.620
0.618
0.619
0.618
0.618
x
…
-2
-1
0
1
2
3
4
…
y
…
-1.15
-2.45
-2.75
-2.05
-0.35
2.35
6.05
…
x
…
-1
0
1
2
4
…
y
…
8
3
0
-1
3
…
北京市丰台区2023-2024学年第一学期九年级期末考试数学试卷: 这是一份北京市丰台区2023-2024学年第一学期九年级期末考试数学试卷,共8页。
2023-2024学年北京市丰台区第一学期初二数学期末试题及答案: 这是一份2023-2024学年北京市丰台区第一学期初二数学期末试题及答案,共10页。
北京市丰台区2023——2024学年上学期九年级期中数学试卷: 这是一份北京市丰台区2023——2024学年上学期九年级期中数学试卷,共10页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。












