2023-2024学年山东省淄博市淄川区七年级（下）期末数学试卷（五四学制）（含答案）

这是一份2023-2024学年山东省淄博市淄川区七年级（下）期末数学试卷（五四学制）（含答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.下列四个选项中的说法不是命题的是( )
A. 对顶角相等B. 过直线外一点作已知直线的平行线
C. 如果a=b，b=c，那么a=cD. 三角形的外角大于任何一个内角
2.已知方程3x−4y=6，用含y的式子表示x为( )
A. x=6−4y3B. x=6+4y3C. y=6−3x4D. y=6+3x4
3.将一副三角板按如图所示的位置摆放在直尺上，则∠1的度数为( )
A. 95°
B. 100°
C. 105°
D. 110°
4.有数字4，5，6的三张卡片，将这三张卡片任意摆成一个三位数，摆出的三位数是5的倍数的概率是( )
A. 16B. 14C. 13D. 12
5.如图，已知AB=DC，∠ABC=∠DCB，能直接判断△ABC≌△DCB的方法是( )
A. SAS
B. AAS
C. SSS
D. ASA
6.已知关于x，y的方程组2x+y=−a+4x+2y=3−a，则x−y的值为( )
A. 1B. a−1C. 0D. −1
7.如图，∠1=70°，直线a//b，则∠2比∠3大( )
A. 70°
B. 80°
C. 110°
D. 180°
8.若x+aay，则( )
A. x0B. xy，a>0D. x>y，a<0
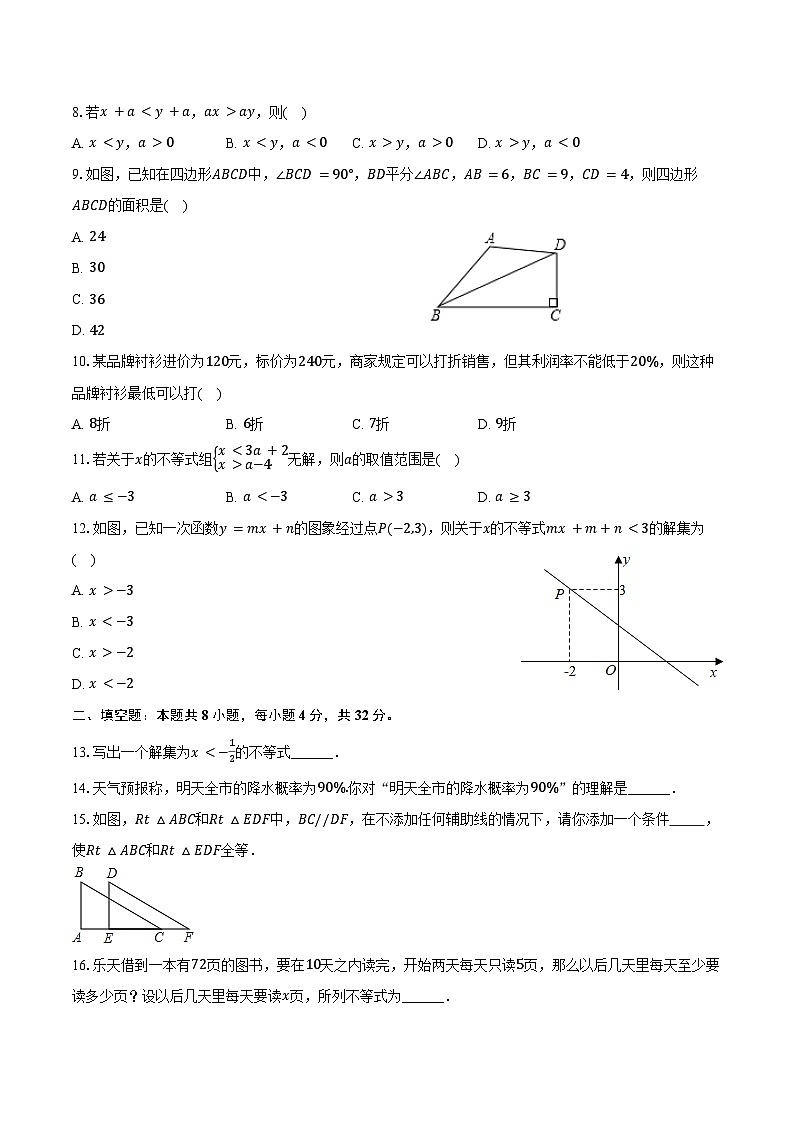
9.如图，已知在四边形ABCD中，∠BCD=90°，BD平分∠ABC，AB=6，BC=9，CD=4，则四边形ABCD的面积是( )
A. 24
B. 30
C. 36
D. 42
10.某品牌衬衫进价为120元，标价为240元，商家规定可以打折销售，但其利润率不能低于20%，则这种品牌衬衫最低可以打( )
A. 8折B. 6折C. 7折D. 9折
11.若关于x的不等式组x<3a+2x>a−4无解，则a的取值范围是( )
A. a≤−3B. a<−3C. a>3D. a≥3
12.如图，已知一次函数y=mx+n的图象经过点P(−2,3)，则关于x的不等式mx+m+n<3的解集为( )
A. x>−3
B. x<−3
C. x>−2
D. x<−2
二、填空题：本题共8小题，每小题4分，共32分。
13.写出一个解集为x<−12的不等式______．
14.天气预报称，明天全市的降水概率为90%.你对“明天全市的降水概率为90%”的理解是______．
15.如图，Rt△ABC和Rt△EDF中，BC/​/DF，在不添加任何辅助线的情况下，请你添加一个条件 ，使Rt△ABC和Rt△EDF全等．
16.乐天借到一本有72页的图书，要在10天之内读完，开始两天每天只读5页，那么以后几天里每天至少要读多少页？设以后几天里每天要读x页，所列不等式为______．
17.如图是由16个相同的小正方形和4个相同的大正方形组成的图形，在这个图形内任取一点P，则点P落在阴影部分的概率是______．
18.如图，过等边△ABC的顶点A，B，C依次作AB，BC，AC的垂线MG，MN，NG，
三条垂线围成△MNG.若AM=2，则△MNG的周长为______．
19.若点M(m+3,m−1)在第四象限，则m的取值范围是______．
20.小慧去花店购买鲜花，若买5支玫瑰和3支百合，则她所带的钱还剩下10元；若买3支玫瑰和5支百合，则她所带的钱还缺4元．若只买8支玫瑰，则她所带的钱还剩下______元．
三、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。
21.(本小题20分)
完成下列各题：
解方程组：
x−y=13,x=6y−7;
12x−32y=−3,2x+3y=3.
解不等式(组)：
2(x−1)+1>−3，
5x+2>3(x−1),12x−1≤7−32x.
22.(本小题8分)
如图，MN//BC，BD⊥DC，∠1=∠2=60°，DC是∠NDE的平分线．
(1)AB与DE平行吗？请说明理由；
(2)试说明∠ABC=∠C；
(3)试说明BD是∠ABC的平分线．
23.(本小题8分)
如图，在△ABC中，∠BAC=60°．
(1)作∠ABC的平分线BD，交AC于点D；作BC的垂直平分线交BD于点E，交BC于点F；(保留痕迹，不写作法)
(2)连接CE，若∠ACE=42°，求∠BEF的度数．
24.(本小题10分)
为了提倡低碳经济，某公司决定购买节省能源的10台新设备，现有甲、乙两种型号的设备，其中每台的价格、产量如下表．
经调查，购买1台甲型设备比购买1台乙型台设备多2万元，购买2台甲型设备比购买3台乙型设备少6万元．
(1)表中a与b的值分别是______；
(2)预算该公司购买节能设备的资金不超过110万元，试通过计算说明公司有几种购买方案可供选择？
(3)在(2)的条件下，若每月要求产量不低于2040吨，为了节省资金，请你为该公司设计一种最省钱的购买方案．
25.(本小题12分)
已知点A(0,4)、C(−2,0)在直线l：y=kx+b上，l和函数y=−4x+a的图象交于点B．
(1)求直线l的表达式；
(2)若点B的横坐标是1，求关于x、y的方程组y=kx+by=−4x+a的解及a的值．
(3)在(2)的条件下，若点A关于x轴的对称点为P，求△PBC的面积．
26.(本小题12分)
两个顶角相等的等腰三角形，如果具有公共的顶角顶点，并把它们的底角顶点连接起来，则形成一组全等的三角形，把具有这个规律的图形称为“手拉手”图形．
(1)问题发现：如图1，若△ABC和△ADE是顶角相等的等腰三角形，BC，DE分别是底边，求证：BD=CE；
(2)解决问题：如图2，若△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE．
①求∠AEB的度数；②判断线段CM，AE，BE之间的数量关系，并说明理由．
参考答案
1.B
2.B
3.C
4.C
5.A
6.A
7.C
8.B
9.B
10.B
11.A
12.A
13.2x<−1(答案不唯一)
14.表明天全市下雨的可能性很大
15.AB=ED(答案不唯一)
16.8x+2×5≥72
17.1350
18.18
19.−320.31
21.解：(1)x−y=13①x=6y−7②，
把②代入①得：6y−7−y=13，
解得y=4，
把y=4代入②得：x=17，
所以方程组的解是x=17y=4．
(2)整理得x−3y=−6①2x+3y=3②，
①+②得：3x=−3，
解得x=−1，
把x=−1代入①得−1−3y=−6，
解得y=53，
所以方程组的解x=−1y=53．
(3)2(x−1)+1>−3，
2x−2+1>−3，
2x>−3+2−1，
2x>−2，
x>−1；
(4)5x+2>3(x−1)①12x−1≤7−32x②，
解不等式①得x>−2.5，
解不等式②得：x≤4，
∴不等式组的解集为−2.522.解：(1)AB//DE，理由如下：
∵MN//BC，( 已知 )
∴∠ABC=∠1=60°.( 两直线平行，内错角相等 )
又∵∠1=∠2，( 已知 )
∴∠ABC=∠2.( 等量代换 )
∴AB//DE.( 同位角相等，两直线平行 )；
(2)∵MN//BC，
∴∠NDE+∠2=180°，
∴∠NDE=180°−∠2=180°−60°=120°．
∵DC是∠NDE的平分线，
∴∠EDC=∠NDC=12∠NDE=60°．
∵MN//BC，
∴∠C=∠NDC=60°．
∴∠ABC=∠C．
(3)∠ADC=180°−∠NDC=180°−60°=120°，
∵BD⊥DC，
∴∠BDC=90°．
∴∠ADB=∠ADC−∠BDC=120°−90°=30°．
∵MN//BC，
∴∠DBC=∠ADB=30°．
∴∠ABD=∠DBC=12∠ABC．
∴BD是∠ABC的平分线．
23.解：(1)作法如图所示；
(2)设∠DBC=x，
∵BD平分∠ABC，
∴∠ABD=∠DBC=x，
∵EF是BC的中垂线，
∴BE=CE，∠BFE=90°，
∴∠ECB=∠DBC=x，
∵∠BAC+∠ACB+∠ABC=180°，
∴60°+42°+x+x+x=180°，
解得：x=26°，
∴∠BEF=90°−∠DBC=90°−26°=64°，
∴∠BEF的度数为64°．
24.：(1)a=12，b=10．
(2)设购买节省能源的新设备甲型设备x台，乙型设备(10−x)台，
则：12x+10(10−x)≤110，
解得：x≤5，
∵x取非负整数∴x=0，1，2，3，4，5，
∴有6种购买方案．
(3)由题意：240x+180(10−x)≥2040，
∴x≥4，
∴x为4或5．
当x=4时，购买资金为：12×4+10×6=108(万元)，
当x=5时，购买资金为：12×5+10×5=110(万元)，
则最省钱的购买方案为：应选购甲型设备4台，乙型设备6台．
25.解：(1)∵点A(0,4)、C(−2,0)在直线l：y=kx+b上，
∴b=4−2k+b=0，解得k=2b=4，
所以直线l的表达式为：y=2x+4；
(2)由于点B在直线l上，当x=1时，y=2+4=6，
所以点B的坐标为(1,6)，
所以关于x、y的方程组y=kx+by=−4x+a的解为x=1y=6，
因为点B是直线l与直线y=−4x+a的交点，
把x=1，y=6代入y=−4x+a中，求得a=10．
(3)因为点A与点P关于x轴对称，所以点P(0,−4)，
所以AP=4+4=8，OC=2，
所以S△BPC=S△PAB+S△PAC
=12×8×1+12×8×2
=4+8
=12．
26.(1)证明：∵△ABC和△ADE是顶角相等的等腰三角形，
∴AB=AC，AD=AE，∠BAC=∠DAE，
∴∠BAC−∠DAC=∠DAE−∠DAC，即∠BAD=∠CAE，
∴△ABD≌△ACE(SAS)，
∴BD=CE；
(2)解：①∵△ACB和△DCE均为等腰直角三角形，
∴AC=BC，DC=EC，∠ACB=90°=∠DCE，
∴∠ACD=∠BCE，
∴△ACD≌△BCE(SAS)，
∴AD=BE，∠ADC=∠BEC，
∵△CDE是等腰直角三角形，
∴∠CDE=∠CED=45°，
∴∠ADC=180°−∠CDE=135°，
∴∠BEC=∠ADC=135°，
∴∠AEB=∠BEC−∠CED=135°−45°=90°，
②结论：AE=BE+2CM，
理由：∵CD=CE，CM⊥DE，
∴DM=ME，
∵∠DCE=90°，
∴DM=ME=CM，
∴DE=2CM，
∴AE=AD+DE=BE+2CM．
甲型
乙型
价格(万元/台)
a
b
产量(吨/月)
240
180