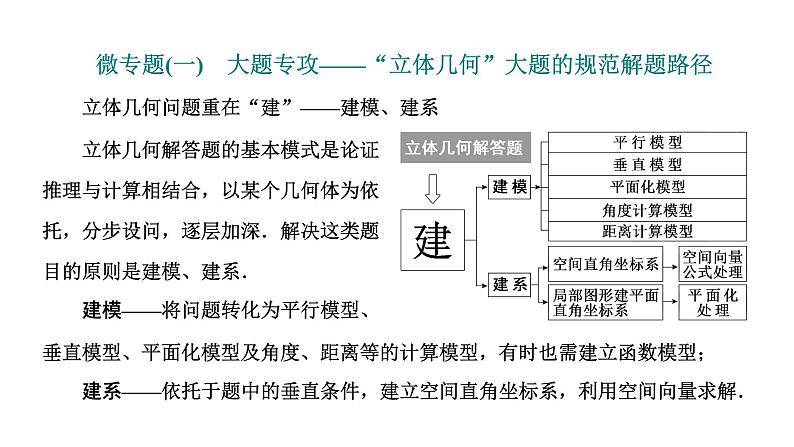
2025年高考数学一轮复习-第三板块-立体几何-微专题(一)大题专攻-“立体几何”大题的规范解题路径【课件】

这是一份2025年高考数学一轮复习-第三板块-立体几何-微专题(一)大题专攻-“立体几何”大题的规范解题路径【课件】，共13页。

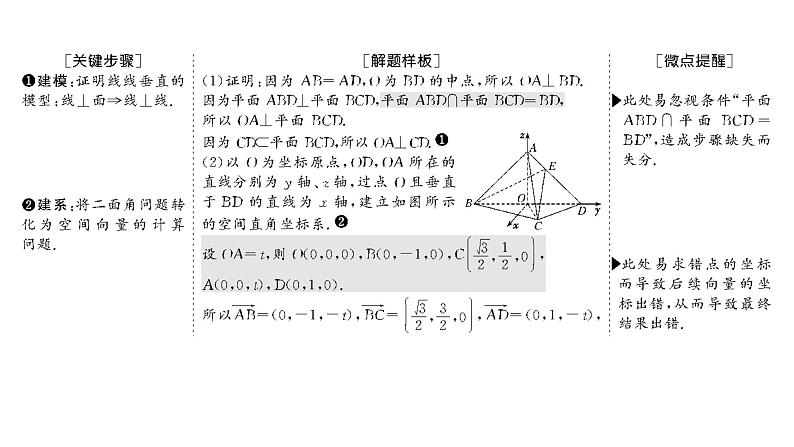
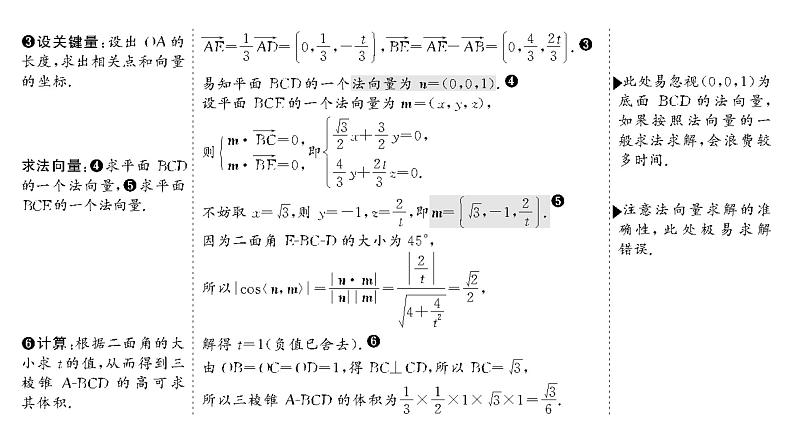
[解题示范][典例]　(2021·新高考Ⅰ卷)如图，在三棱锥A-BCD中，平面ABD⊥平面BCD，AB＝AD，O为BD的中点．(1)证明：OA⊥CD.(2)若△OCD是边长为1的等边三角形，点E在棱AD上，DE＝2EA，且二面角E-BC-D的大小为45°，求三棱锥A-BCD的体积．
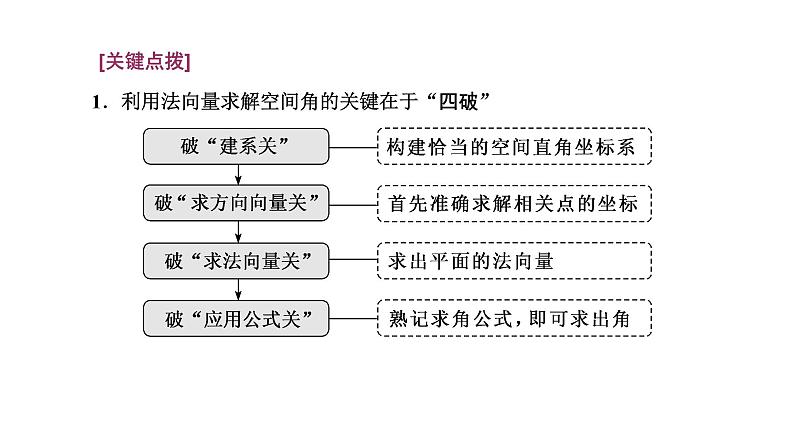
[关键点拨]1．利用法向量求解空间角的关键在于“四破”
2．解答立体几何问题，应具备以下5点思维(1)由于空间图形问题往往可转化为平面图形问题加以解决，因此要注意平面几何知识在解题中的灵活运用．例如，证线线平行可以利用三角形、梯形的中位线性质定理，还可以利用比例关系；证线线垂直可以利用菱形、正方形的对角线互相垂直，还可以利用勾股定理的逆定理．(2)立体几何中证明有关平行或垂直问题时，由于大多数问题主要考查的是有关判定定理在证题中的灵活运用，所以我们要优先考虑对应的判定定理去寻找证题思路．
(3)立体几何中证明有关平行或垂直问题时，若对应的判定定理不便于运用，则应该及时考虑其他的证题思路．例如，要证线面平行，可以先证面面平行，再利用面面平行的性质；要证明线面垂直，可以先证面面垂直，再利用面面垂直的性质．(4)分析、解决有关立体几何问题时，往往需要考虑数形结合思想、分类与整合思想、转化思想在解题中的灵活应用．(5)由于立体几何解答题侧重考查空间向量法在解题中的灵活运用，所以必须熟练掌握利用空间向量法求解空间角的具体过程．
[应用体验](2022·全国乙卷)如图，四面体ABCD中，AD⊥CD，AD＝CD，∠ADB＝∠BDC，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设AB＝BD＝2，∠ACB＝60° ，点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成的角的正弦值．解：(1)证明：因为AD＝CD，∠ADB＝∠CDB，DB＝DB，所以△ADB≌△CDB，所以AB＝BC.因为E为AC的中点，所以AC⊥BE，AC⊥DE，又BE∩DE＝E，BE，DE⊂平面BED，所以AC⊥平面BED，又AC⊂平面ACD，所以平面BED⊥平面ACD.
“课时验收评价”见“课时验收评价(五)” (单击进入电子文档)