北师版高中数学必修第一册4.3对数函数4.3.1~4.3.2（课件）

这是一份北师版高中数学必修第一册4.3对数函数4.3.1~4.3.2（课件），共24页。

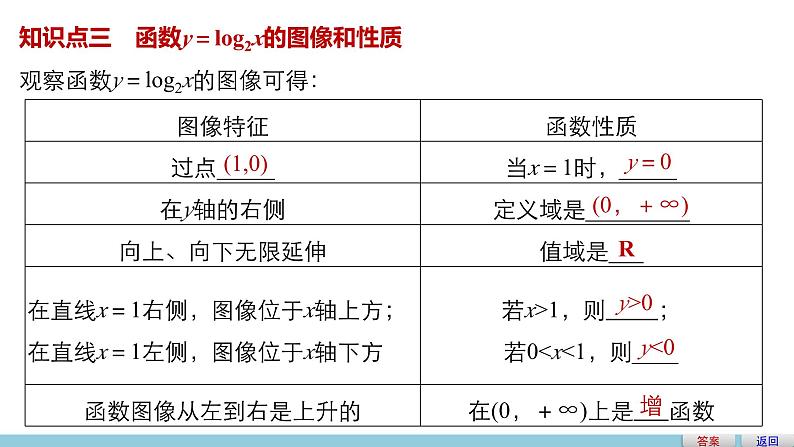
4.3.1　对数函数的概念4.3.2　对数函数y＝log2x的图像和性质1.理解对数函数的概念以及对数函数与指数函数间的关系；2.了解指数函数与对数函数互为反函数，并会求指数函数或对数函数的反函数；3.会画具体函数的图像.问题导学题型探究达标检测学习目标知识点一　对数函数思考　你能把指数式y＝ax(a>0，a≠1)化成对数式吗？在这个对数式中，x是y的函数吗？答案　根据对数的定义，得x＝logay(a>0，a≠1).因为y＝ax是单调函数，每一个y都有唯一确定的x与之对应，所以x是y的函数.答案问题导学 　　　　新知探究 点点落实答案一般地，我们把函数y＝logax(a>0，a≠1)叫作对数函数，a叫作对数函数的 ，x是 ，定义域是 ，值域是 .两类特殊的对数函数常用对数函数：y＝lg x，其底数为 .自然对数函数：y＝ln x，其底数为无理数 .底数真数(0，＋∞)R10e答案知识点二　反函数思考　函数y＝ax的定义域和值域与y＝logax的定义域和值域有什么关系？答案　对数函数y＝logax的定义域是指数函数y＝ax的值域，对数函数y＝logax的值域是指数函数y＝ax的定义域.指数函数y＝ax(a>0，a≠1)是对数函数 的反函数；同时对数函数y＝logax(a>0，a≠1)也是 的反函数，即同底的指数函数与对数函数互为反函数.y＝logax(a>0，a≠1)指数函数y＝ax(a>0，a≠1)知识点三　函数y＝log2x的图像和性质观察函数y＝log2x的图像可得：(1,0)y＝0(0，＋∞)Ry>0y<0增答案返回解析答案反思与感悟题型探究 　　　　重点难点 个个击破类型一　对数函数的概念解　设y＝logax(a>0且a≠1)，则2＝loga4，故a＝2，即y＝log2x，判断一个函数是否为对数函数的方法判断一个函数是对数函数必须是形如y＝logax(a>0且a≠1)的形式，即必须满足以下条件：①系数为1.②底数为大于0且不等于1的常数.③对数的真数仅有自变量x.跟踪训练1　判断下列函数是不是对数函数？并说明理由.(1)y＝logax2(a>0，且a≠1)；(2)y＝log2x－1；(3)y＝logxa(x>0，且x≠1)；(4)y＝log5x.解　∵(1)中真数不是自变量x，∴不是对数函数；∵(2)中对数式后减1，∴不是对数函数；∵(3)中底数是自变量x，而非常数a，∴不是对数函数.(4)为对数函数.解析答案解析答案类型二　对数函数的定义域例2　求下列函数的定义域：(1)y＝loga(9－x2)；解　由9－x2>0，得－30，得4x<16＝42，由指数函数的单调性得x<2，∴函数y＝log2(16－4x)的定义域为{x|x<2}.反思与感悟　求含对数式的函数定义域关键是真数大于0，底数大于0且不为1.反思与感悟解析答案跟踪训练2　求下列函数的定义域：∴x≥1，∴所求函数定义域为{x|x≥1}.解析答案类型三　求反函数例3　求下列函数的反函数：(1)y＝10x；解　指数函数y＝10x，它的底数是10，它的反函数是对数函数y＝lg x.解析答案(3)解　对数函数(4)y＝log7x.解　对数函数y＝log7x，它的底数是7，它的反函数是指数函数y＝7x.反思与感悟　同底的指数函数、对数函数互为反函数.反思与感悟解析答案跟踪训练3　写出下列函数的反函数(用x表示自变量，y表示函数)：(1)y＝2.5x；解　函数y＝2.5x的反函数是y＝log2.5x(x>0).(2)解析答案类型四　函数y＝log2x的图像与性质例4　根据函数f(x)＝log2x的图像和性质求解以下问题：(1)若f(a)>f(2)，求a的取值范围；(2)求y＝log2(2x－1)在x∈[2,14]上的最值.解　函数y＝log2x的图像如图.(1)∵y＝log2x是增函数，若f(a)>f(2)，即log2a>log22，则a>2.∴a的取值范围为(2，＋∞).(2)∵2≤x≤14，∴3≤2x－1≤27，∴函数y＝log2(2x－1)在x∈[2,14]上的最小值为log23，最大值为log227.∴log23≤log2(2x－1)≤log227.反思与感悟函数f(x)＝log2x是最基本的对数函数.它在(0，＋∞)上是单调递增的.利用单调性可以解不等式，求函数值域，比较对数值的大小.解　函数f(x)＝log2x在(0，＋∞)上为增函数，(2)若log2(2－x)>0，求x的取值范围.解　log2(2－x)>0，即log2(2－x)>log21，∵函数y＝log2x为增函数，∴2－x>1，即x<1.∴x的取值范围为(－∞，1).解析答案返回123解析答案达标检测41.函数f(x)＝lg(x－1)＋ 的定义域为(　　)A.(1,4] B.(1,4)C.[1,4] D.[1,4)5A解析答案2.函数y＝log2x在[1,2]上的值域是(　　)A.R B.(－∞，1]C.[0,1] D.[0，＋∞)解析　∵1≤x≤2，∴log21≤log2x≤log22.即0≤y≤1.12345C解析答案3.函数y＝ln x的反函数是______.解析　同底的对数函数与指数函数互为反函数.12345y＝ex解析答案12345如图所示.由图知它们的图像只有一个交点，1解析答案12345返回1.解与对数有关的问题，首先要保证在定义域范围内解题，即真数大于零，底数大于零且不等于1，函数定义域的结果一定要写成集合或区间的形式.2.指数函数y＝ax与对数函数y＝logax互为反函数，它们定义域与值域互反，图像关于直线y＝x对称.3.应注意数形结合思想在解题中的应用.本课结束