

2023-2024学年贵州省遵义市绥阳县八年级上学期期中数学试题及答案
展开1.(3分)下列道路交通指示标志图是轴对称图形的是( )
A.B.C.D.
2.(3分)下列长度四根木棒中,能与长为4,9的两根木棒围成一个三角形的是( )
A.4B.5C.9D.14
3.(3分)在直角坐标系中,点A(2,﹣8)、B关于y轴对称,则点B的坐标是( )
A.(﹣2,﹣8)B.(2,8)C.(﹣2,8)D.(8,2)
4.(3分)小刚把一块三角形玻璃打碎成了如图所示的三块,现要到玻璃店取配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去B.带②去C.带③去D.带①和②去
5.(3分)如图,已知l∥AB,CD⊥l于点D,若∠C=40°,则∠1的度数是( )
A.30°B.40°C.50°D.60°
6.(3分)内角和等于外角和2倍的多边形是( )
A.五边形B.六边形C.七边形D.八边形
7.(3分)如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠B=∠EB.∠BCA=∠FC.BC∥EFD.∠A=∠EDF
8.(3分)若等腰三角形有两条边的长度为5和8,则此等腰三角形的周长为( )
A.18或21B.21C.24或18D.18
9.(3分)如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=5,AC=4,则△ADC的周长为( )
A.7B.8C.9D.10
10.(3分)如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△ABC=4cm2,则S△BEF等于( )
A.2cm2B.1cm2C.12cm2D.14cm2
11.(3分)如图,在△ABC中,AB=AC,点E在BC边上,在线段AC的延长线上取点D,使得CD=CE,连接DE,CF是△CDE的中线,若∠FCE=52°,则∠A的度数为( )
A.38°B.34°C.32°D.28°
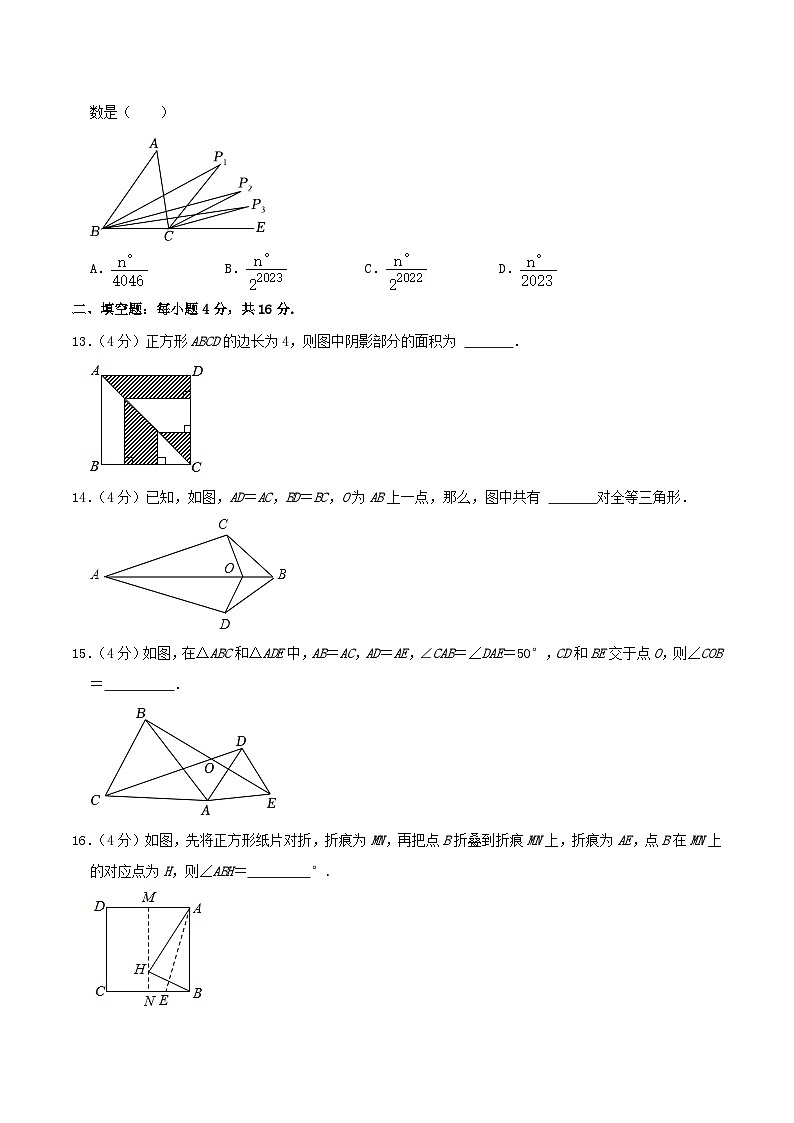
12.(3分)如图,已知∠A=n°,若P1点是∠ABC和外角∠ACE的角平分线的交点,P2点是∠P1BC和外角∠P1CE的角平分线的交点,P3点是∠P2BC和外角∠P2CE的角平分线的交点,…,以此类推,则∠P2023的度数是( )
A.B.C.D.
二、填空题:每小题4分,共16分.
13.(4分)正方形ABCD的边长为4,则图中阴影部分的面积为 .
14.(4分)已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有 对全等三角形.
15.(4分)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=50°,CD和BE交于点O,则∠COB= .
16.(4分)如图,先将正方形纸片对折,折痕为MN,再把点B折叠到折痕MN上,折痕为AE,点B在MN上的对应点为H,则∠ABH= °.
三、解答题:本大题共9题,共计98分,解答应写出必要的文字说明,证明过程或
17.(8分)“西气东输”是造福子孙后代的创世工程,现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇等距离,请你画出中心站的位置.(尺规作图,保留痕迹)
18.(10分)已知,如图,AC=FE,BC=DE,点A、D、B、F在一条直线上,AD=BF.求证:∠E=∠C.
小红的解答如下:
证明:在△ACB和△FED中,
∵AC=FE,BC=DE,AD=BF…第一步,
∴△ACB≌△FED…第二步,
∴∠E=∠C…第三步,
(1)小红的证明过程从第 步开始出现错误;
(2)请写出你认为正确的证明过程.
19.(10分)如图,在△ABC中,已知AD是角平分线,∠B=62°,∠C=58°.
(1)求∠BAD的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
20.(10分)如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,求证:BD+EC=DE.
21.(12分)△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)在图中作出△ABC关于y轴对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标;
(3)在x轴上求作一点P,使PA+PB1最短.(不写作法,写出结论)
22.(12分)如图,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.
23.(12分)公路上,A,B两站相距25千米,C、D为两所学校,DA⊥AB于点A,CB⊥AB于点B,如图,已知DA=15千米,现在要在公路AB上建一报亭H,使得C、D两所学校到H的距离相等,且∠DHC=90°,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?
24.(12分)如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,若BD=CD.
(1)求证:BE=CF;
(2)已知AB=10,AC=18,求BE的长.
25.(12分)数学兴趣活动课上,小明将等腰△ABC的底边BC与直线l重合,问:
(1)已知AB=AC=6,∠BAC=120°,点P在BC边所在的直线l上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小明发现AP的最小值是 ;
(2)为进一步运用该结论,小明发现当AP最短时,在Rt△ABP中,∠P=90°,作了AD平分∠BAP,交BP于点D,点E、F分别是AD、AP边上的动点,连接PE、EF,小明尝试探索PE+EF的最小值,为转化EF,小明在AB上截取AN,使得AN=AF,连接NE,易证△AEF≌△AEN,从而将PE+EF转化为PE+EN,转化到(1)的情况,若BP=3,AB=6,AP=3,则PE+EF的最小值为 ;
(3)请应用以上转化思想解决问题(3),在直角△ABC中,∠C=90°,∠B=30°,AC=10,点D是CB边上的动点,连接AD,将线段AD顺时针旋转60°,得到线段AP,连接CP,求线段CP的最小值.
2023-2024学年贵州省遵义市绥阳县八年级(上)期中数学试卷
(参考答案)
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
1.(3分)下列道路交通指示标志图是轴对称图形的是( )
A.B.C.D.
【解答】解:A,C,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
2.(3分)下列长度四根木棒中,能与长为4,9的两根木棒围成一个三角形的是( )
A.4B.5C.9D.14
【解答】解:设第三边为c,则9﹣4<c<9+4,即5<c<13.只有9符合要求.
故选:C.
3.(3分)在直角坐标系中,点A(2,﹣8)、B关于y轴对称,则点B的坐标是( )
A.(﹣2,﹣8)B.(2,8)C.(﹣2,8)D.(8,2)
【解答】解:∵点A与点B关于y轴对称,点A的坐标是(2,﹣8),
∴点B的坐标是:(﹣2,﹣8).
故选:A.
4.(3分)小刚把一块三角形玻璃打碎成了如图所示的三块,现要到玻璃店取配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去B.带②去C.带③去D.带①和②去
【解答】解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
5.(3分)如图,已知l∥AB,CD⊥l于点D,若∠C=40°,则∠1的度数是( )
A.30°B.40°C.50°D.60°
【解答】解:在Rt△CDE中,∠CDE=90°,∠DCE=40°,
则∠CED=90°﹣40°=50°,
∵l∥AB,
∴∠1=∠CED=50°,
故选:C.
6.(3分)内角和等于外角和2倍的多边形是( )
A.五边形B.六边形C.七边形D.八边形
【解答】解:设这个多边形的边数为n,则依题意可得:
(n﹣2)×180°=360°×2,
解得n=6,
∴这个多边形的边数为6.
故选:B.
7.(3分)如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠B=∠EB.∠BCA=∠FC.BC∥EFD.∠A=∠EDF
【解答】解:A、∵AB=DE,BC=EF,∠B=∠E,
∴△ABC≌△DEF(SAS),
故A符合题意;
B、∵AB=DE,BC=EF,∠BCA=∠F,
∴不能使△ABC≌△DEF,
故B不符合题意;
C∵BC∥EF,
∴∠BCA=∠F,
∵AB=DE,BC=EF,∠BCA=∠F,
∴不能使△ABC≌△DEF,
故C不符合题意;
D、∵AB=DE,BC=EF,∠A=∠EDF,
∴不能使△ABC≌△DEF,
故D不符合题意;
故选:A.
8.(3分)若等腰三角形有两条边的长度为5和8,则此等腰三角形的周长为( )
A.18或21B.21C.24或18D.18
【解答】解:根据题意,
①当腰长为5时,周长=5+5+8=18;
②当腰长为8时,周长=8+8+5=21.
故选:A.
9.(3分)如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=5,AC=4,则△ADC的周长为( )
A.7B.8C.9D.10
【解答】解:∵DE垂直平分线段BC,
∴DB=DC,
∵AB=5,AC=4,
∴△ADC的周长为:AD+CD+AC=AB+AC=5+4=9.
故选:C.
10.(3分)如图,在△ABC中,D,E,F分别是BC,AD,CE的中点,S△ABC=4cm2,则S△BEF等于( )
A.2cm2B.1cm2C.12cm2D.14cm2
【解答】解:∵由于D、E、F分别为BC、AD、CE的中点,
∴△ABE、△DBE、△DCE、△AEC的面积相等,
S△BEC=S△ABC=2(cm2).
S△BEF=S△BEC=×2=1(cm2).
故选:B.
11.(3分)如图,在△ABC中,AB=AC,点E在BC边上,在线段AC的延长线上取点D,使得CD=CE,连接DE,CF是△CDE的中线,若∠FCE=52°,则∠A的度数为( )
A.38°B.34°C.32°D.28°
【解答】解:∵CE=CD,FE=FD,
∴∠ECF=∠DCF=52°,
∴∠ACB=180°﹣104°=76°,
∵AB=AC,
∴∠B=∠ACB=76°,
∴∠A=180°﹣152°=28°,
故选:D.
12.(3分)如图,已知∠A=n°,若P1点是∠ABC和外角∠ACE的角平分线的交点,P2点是∠P1BC和外角∠P1CE的角平分线的交点,P3点是∠P2BC和外角∠P2CE的角平分线的交点,…,以此类推,则∠P2023的度数是( )
A.B.C.D.
【解答】解:∵BP1平分∠ABC,CP1平分∠ACE,
∴∠P1BC=∠ABC,∠P1CE=∠ACE,
∵∠ACE=∠A+∠ABC,∠P1CE=∠P1+∠P1BC,
∴∠P1=∠A,同理∠BP2C=∠BP1C,
∠BP3C=∠BP2C,
由此可发现规律∠BPnC=∠A=.
∴∠P2023=,
故选:B.
二、填空题:每小题4分,共16分.
13.(4分)正方形ABCD的边长为4,则图中阴影部分的面积为 8 .
【解答】解:由图形可得:
S阴影=•S正方形ABCD=×4×4=8.
故答案为:8.
14.(4分)已知,如图,AD=AC,BD=BC,O为AB上一点,那么,图中共有 3 对全等三角形.
【解答】解:∵AD=AC,BD=BC,AB=AB,
∴△ADB≌△ACB;
∴∠CAO=∠DAO,∠CBO=∠DBO,
∵AD=AC,BD=BC,OA=OA,OB=OB
∴△ACO≌△ADO,△CBO≌△DBO.
∴图中共有3对全等三角形.
故答案为:3.
15.(4分)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=50°,CD和BE交于点O,则∠COB= 50° .
【解答】解:∵∠CAB=∠DAE,
∴∠CAD=∠BAE,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴∠ACD=∠ABE,
∵∠CAB=50°,
∴∠ACB+∠ABC=180°﹣50°=130°,
∵∠ACB+∠ABC=∠ACD+∠BCO+∠ABC,∠ACD=∠ABE,
∴∠ACB+∠ABC=∠BCO+∠ABC+∠ABE=∠BCO+∠CBO,
∴∠BCO+∠CBO=130°,
∴∠COB=180°﹣130°=50°,
故答案为:50°.
16.(4分)如图,先将正方形纸片对折,折痕为MN,再把点B折叠到折痕MN上,折痕为AE,点B在MN上的对应点为H,则∠ABH= 75 °.
【解答】解:连接DH,
由折叠可得,MN垂直平分AD,AB=AH,
∴DH=AH=AB=AD,
∴△ADH是等边三角形,
∴∠DAH=60°,
又∵∠BAD=90°,
∴∠BAH=30°,
∵AH=AB,
∴∠ABH=×(180°﹣30°)=75°.
故答案为:75.
三、解答题:本大题共9题,共计98分,解答应写出必要的文字说明,证明过程或
17.(8分)“西气东输”是造福子孙后代的创世工程,现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇等距离,请你画出中心站的位置.(尺规作图,保留痕迹)
【解答】解:如图所示:
.
18.(10分)已知,如图,AC=FE,BC=DE,点A、D、B、F在一条直线上,AD=BF.求证:∠E=∠C.
小红的解答如下:
证明:在△ACB和△FED中,
∵AC=FE,BC=DE,AD=BF…第一步,
∴△ACB≌△FED…第二步,
∴∠E=∠C…第三步,
(1)小红的证明过程从第 一 步开始出现错误;
(2)请写出你认为正确的证明过程.
【解答】解:(1)小红的证明过程从第一步开始出现错误,
故答案为:一;
(2)∵AD=BF,
∴AD+BD=BF+BD,
即AB=FD,
在△FED和△ACB中,
,
∴△FED△ACB≌(SSS),
∴∠E=∠C,
19.(10分)如图,在△ABC中,已知AD是角平分线,∠B=62°,∠C=58°.
(1)求∠BAD的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
【解答】解:(1)∵在△ABC中,∠B=62°,∠C=58°,∠BAC+∠B+∠C=180°,
∴∠BAC=180°﹣∠B﹣∠C=60°.
∵AD是△ABC的角平分线,
∴∠BAD=∠BAC=30°;
(2)∵∠CAD=∠BAC=30°,DE⊥AC,
∴在Rt△ADE中,∠EAD=30°,
∴∠ADE=90°﹣∠EAD=60°.
20.(10分)如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,求证:BD+EC=DE.
【解答】证明:∵BF、CF是∠ABC、∠ACB的角平分线,
∴∠DBF=∠FBC,∠ECF=∠BCF.
又∵DE∥BC,
∴∠BFD=∠CBF,∠BCF=∠EFC.
∴∠DBF=∠DFB,∠ECF=∠EFC.
∴BD=DF,CE=EF.
∴DE=DF+EF=BD+CE.
21.(12分)△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)在图中作出△ABC关于y轴对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标;
(3)在x轴上求作一点P,使PA+PB1最短.(不写作法,写出结论)
【解答】解:(1)如图,△A1B1C1即为所求.
(2)A1(﹣2,4)、B1(﹣1,1)、C1(﹣3,2).
(3)如图,点P即为所求.
22.(12分)如图,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.
【解答】证明:(1)∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE;
(2)∵△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
23.(12分)公路上,A,B两站相距25千米,C、D为两所学校,DA⊥AB于点A,CB⊥AB于点B,如图,已知DA=15千米,现在要在公路AB上建一报亭H,使得C、D两所学校到H的距离相等,且∠DHC=90°,问:H应建在距离A站多远处?学校C到公路的距离是多少千米?
【解答】解:∵∠DHC=90°,
∴∠AHD+∠CHB=90°,
∵DA⊥AB,
∴∠D+∠AHD=90°,
∴∠D=∠CHB,
在△ADH和△BHC中,,
∴△ADH≌△BHC(AAS),
∴AD=BH=15千米,AH=BC,
∵A,B两站相距25千米,
∴AB=25千米,
∴AH=AB﹣BH=25﹣15=10千米,
∴学校C到公路的距离是10千米.
答:H应建在距离A站10千米处,学校C到公路的距离是10千米.
24.(12分)如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,若BD=CD.
(1)求证:BE=CF;
(2)已知AB=10,AC=18,求BE的长.
【解答】(1)证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F.
∴DE=DF,∠E=∠DFC=90°,
在Rt△DBE和Rt△DCF中,
,
∴Rt△DBE≌Rt△DCF(HL),
∴BE=CF;
(2)解:由(1)得DE=DF,∠E=∠DFC=90°,BE=CF
在△ADE 和△ADF中
∴Rt△ADE≌Rt△ADF(AAS),
∴AE=AF,
∴AB+BE=AC﹣CF,
即10+BE=18﹣CF,
10+BE=18﹣BE,
BE=4.
25.(12分)数学兴趣活动课上,小明将等腰△ABC的底边BC与直线l重合,问:
(1)已知AB=AC=6,∠BAC=120°,点P在BC边所在的直线l上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小明发现AP的最小值是 3 ;
(2)为进一步运用该结论,小明发现当AP最短时,在Rt△ABP中,∠P=90°,作了AD平分∠BAP,交BP于点D,点E、F分别是AD、AP边上的动点,连接PE、EF,小明尝试探索PE+EF的最小值,为转化EF,小明在AB上截取AN,使得AN=AF,连接NE,易证△AEF≌△AEN,从而将PE+EF转化为PE+EN,转化到(1)的情况,若BP=3,AB=6,AP=3,则PE+EF的最小值为 ;
(3)请应用以上转化思想解决问题(3),在直角△ABC中,∠C=90°,∠B=30°,AC=10,点D是CB边上的动点,连接AD,将线段AD顺时针旋转60°,得到线段AP,连接CP,求线段CP的最小值.
【解答】解:(1)如图1中,作AH⊥BC于H.
∵AB=AC=6,AH⊥BC,
∴∠BAH=∠CAH=∠BAC=60°,
∴AH=AB•cs60°=3,
根据垂线段最短可知,当AP与AH重合时,PA的值最小,最小值为3.
故答案为3.
(2)如图2中,在AB上截取AN,使得AN=AF,连接NE.作PH⊥AB于H.
∵∠EAN=∠EAF,AN=AF,AE=AE,
∴△EAN≌△EAF(SAS),
∴EN=EF,
∴PE+EF=PE+NE,
∴当P,E,N共线且与PH重合时,PE+PF的值最小,最小值为线段PH的长,
∵•AB•PH=•PA•PB,
∴PH==,
∴PE+EF的最小值为.
故答案为.
(3)如图3中,在AB上取一点K,使得AK=AC,连接CK,DK.
∵∠ACB=90°,∠B=30°,
∴∠CAK=60°,
∴∠PAD=∠CAK,
∴∠PAC=∠DAK,
∵PA=DA,CA=KA,
∴△PAC≌△DAK(SAS),
∴PC=DK,
∵KD⊥BC时,KD的值最小,最小值为5,
∴PC的最小值为5.
贵州省遵义市绥阳县实验中学2023-2024学年八年级下学期3月考数学试题(无答案): 这是一份贵州省遵义市绥阳县实验中学2023-2024学年八年级下学期3月考数学试题(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
20,贵州省遵义市绥阳县2023-2024学年八年级上学期期中数学试题: 这是一份20,贵州省遵义市绥阳县2023-2024学年八年级上学期期中数学试题,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
贵州省遵义市绥阳县2023-2024学年七年级上学期期中数学试卷: 这是一份贵州省遵义市绥阳县2023-2024学年七年级上学期期中数学试卷,共16页。试卷主要包含了选择题等内容,欢迎下载使用。












