
所属成套资源:沪教版暑假新九年级数学考点讲与练(原卷版+解析)
沪教版暑假新九年级数学考点讲与练第12讲二次函数的应用(考点讲与练)(原卷版+解析)
展开
这是一份沪教版暑假新九年级数学考点讲与练第12讲二次函数的应用(考点讲与练)(原卷版+解析),共28页。
二次函数的应用
(1)利用二次函数解决利润问题
在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.
(2)几何图形中的最值问题
几何图形中的二次函数问题常见的有:几何图形中面积的最值,用料的最佳方案以及动态几何中的最值的讨论.
(3)构建二次函数模型解决实际问题
利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.
【考点剖析】
利润问题
1.(2023秋•虹口区校级期末)某品牌裙子,平均每天可以售出20条,每条盈利40元,经市场调查发现,如果该品牌每条裙子每降价1元,那么平均每天可以多售出2条,那么当裙子降价 元时,可获得最大利润 元.
2.(2023春•嘉定区校级期中)某超市从厂家购进A、B两种型号的水杯,两次购进水杯的情况如表:
(1)求A、B两种型号的水杯进价各是多少元?
(2)在销售过程中,A型水杯因为物美价廉而更受消费者喜欢.为了增大B型水杯的销售量,超市决定对B型水杯进行降价销售,当销售价为44元时,每天可以售出20个,每降价1元,每天将多售出5个,请问超市应将B型水杯降价多少元时,每天售出B型水杯的利润达到最大?最大利润是多少?
3.(2023春•徐汇区校级月考)某工厂设计了一款产品,成本为每件20元.投放市场进行试销,经调查发现,该种产品每天的销售量y(件)与销售单价x(元)之间满足一次函数的关系,其中20≤x≤40.
(1)根据表格求y关于x的函数解析式;
(2)设销售这种产品每天的利润为W(元),求W关于销售单价x之间的函数解析式并求当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
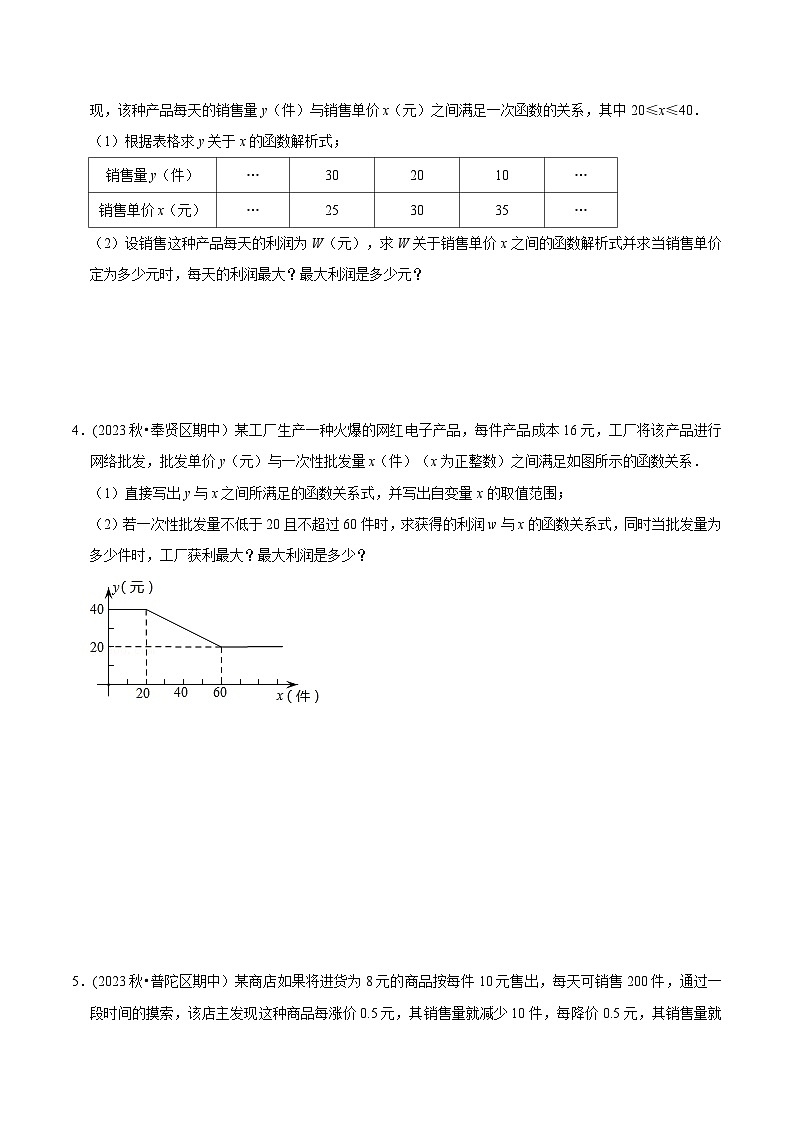
4.(2023秋•奉贤区期中)某工厂生产一种火爆的网红电子产品,每件产品成本16元,工厂将该产品进行网络批发,批发单价y(元)与一次性批发量x(件)(x为正整数)之间满足如图所示的函数关系.
(1)直接写出y与x之间所满足的函数关系式,并写出自变量x的取值范围;
(2)若一次性批发量不低于20且不超过60件时,求获得的利润w与x的函数关系式,同时当批发量为多少件时,工厂获利最大?最大利润是多少?
5.(2023秋•普陀区期中)某商店如果将进货为8元的商品按每件10元售出,每天可销售200件,通过一段时间的摸索,该店主发现这种商品每涨价0.5元,其销售量就减少10件,每降价0.5元,其销售量就增加10件.
(1)如果每天的利润要达到700元,售价应定为每件多少元?
(2)将售价定为每件多少元时,能使这天所获利润最大?最大利润是多少?
最值问题
1.(2023秋•松江区期末)一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为y=−112x2+23x+53,那么铅球运动过程中最高点离地面的距离为 米.
2.(2023秋•静安区校级月考)如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,当球飞越的水平距离为8米时,球到达最高点B处,离地面高度为9米,则这个二次函数的表达式为 ,小孩将球抛出了约 米(精确到0.1m).
3.(2023秋•杨浦区校级期中)某建筑工程队在工地一边的靠墙处,用120米长的铁栅栏围成一个所占面积为长方形的临时仓库,其中墙仅80米长,铁栅栏只围三边,则所围仓库的最大面积为 平方米.
构建二次函数模型解决实际问题
1.(2023秋•虹口区期末)如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.45米B.10米C.46米D.12米
2.(2023•宝山区二模)有一座抛物线拱型桥,在正常水位时,水面BC的宽为10米,拱桥的最高点D到水面BC的距离DO为4米,点O是BC的中点,如图,以点O为原点,直线BC为x,建立平面直角坐标系xOy.
(1)求该抛物线的表达式;
(2)如果水面BC上升3米(即OA=3)至水面EF,点E在点F的左侧,求水面宽度EF的长.
四、二次函数与几何图形
1.(2023•宝山区模拟)在一块等腰直角三角形铁皮上截一块矩形铁皮.如图,已有的铁皮是等腰直角三角形ABC,它的底边AB长20厘米.要截得的矩形EFGD的边FG在AB上,顶点E、D分别在边CA、CB上.设EF的长为x厘米,矩形EFGD的面积为y平方厘米,试写出y关于x的函数解析式及定义域,并求当EF的长为4厘米时所截得的矩形的面积.
2.(2023秋•浦东新区校级月考)将一条长20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这两段铁丝的长度分别为多少?
(2)两个正方形的面积之和可能等于12cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
(3)两个正方形的面积之和最小为 cm2.
3.(2023秋•浦东新区校级月考)如图,在直角三角形ABC中,直角边AC=6cm,BC=8cm,设P,Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm.当P点到达B点时,Q点就停止移动,设P,Q移动的时间t秒.
(1)写出△PBQ的面积S(cm2)与时间t(s)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,△PBQ为等腰三角形?
4.(2023春•金山区期末)如图,正方形ABCD,AB=4,点M是边BC的中点,点E是边AB上的一个动点,作EG⊥AM交AM于点G,EG的延长线交线段CD于点F.
(1)如图①,当点E与点B重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD的面积为y,求y与x的函数解析式,并写出定义域.
5.(2023春•长宁区期末)已知在等腰梯形ABCD中,AD∥BC,AD=AB=CD=6厘米,∠B=60°,点P在边AD上以每秒2厘米的速度从D出发,向点A运动;点Q在边AB上以每秒1厘米的速度从点B出发,向点A运动.已知P、Q两点同时出发,当其中一个点到达终点时,另外一个点也随之停止运动,设两个点的运动时间为t秒,联结PC、QD.
(1)如图1,若四边形BQDC的面积为S平方厘米,求S关于t的函数解析式并写出函数定义域;
(2)若PC与QD相交于点E,且∠PEQ=60°,求t的值.
【过关检测】
1.(2023·上海九年级专题练习)如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.
(1)当矩形DEFG是正方形时,求正方形的边长.
(2)设EF=x,矩形DEFG的面积为S,求S关于x的函数关系式,当x为何值时S有最大值,并求出最大值.
2.(2023·上海九年级专题练习)商场购进某种新商品在试销期间发现,当每件利润为10元时,每天可销售70件;当每件商品每涨价1元,日销售量就减少1件,但每天的销售量不得低于35件.据此规律,请回答下列问题.
(1)设每件涨了x元时,每件盈利_________元,商品每天可销售______件;
(2)在商品销售正常的情况下,每件商品涨价多少元时,商场每天盈利为1500元?
(3)若商场的每天盈利能达到最大,请直接写出每天的最大盈利为______________.
3.(2023·上海九年级专题练习)某电动机加工厂以400元/个的价格新接了一批电动机加工业务.根据工厂以往的制造能力,该工厂每天制造电动机的数量为x(个)(200≤x≤500),且每个电动机的制造成本y(元)与每天制造电动机的数量x(个)之间的函数关系的图象如图所示.
(1)求y与x之间的函数表达式;
(2)已知该工厂每天各项消耗的费用是2万元,每天的利润为w元,请求出w与x之间的函数表达式,并求出当x为多少时,w最大,最大日利润是多少.
4.(2023秋•浦东新区月考)阅读材料:
配方法可以用来解一元二次方程,还可以用它来解决一些最值问题,比如:因为3a2≥0,所以3a2+1就有个最小值1,即3a2+1≥1,只有当a=0时,才能得到这个式子的最小值1.同样,因为﹣3a2≤0,所以﹣3a2+1有最大值1,即﹣3a2+1≤1,只有在a=0时,才能得到这个式子的最大值1.
请解决下列问题:
(1)当x= 时,代数式3(x﹣2)2﹣1有最 (填“大”或“小”)值为 ;
(2)当x= 时,代数式﹣2x2﹣4x+3有最 (填“大”或“小”)值为 ;
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度16m,求:当花园与墙相邻(即垂直于墙)的边长为多少时,花园的面积最大?最大面积是多少?
进货批次
A型水杯(个)
B型水杯(个)
总费用(元)
一
100
200
8000
二
200
300
13000
销售量y(件)
…
30
20
10
…
销售单价x(元)
…
25
30
35
…
第12讲 二次函数的应用(核心考点讲与练)
【基础知识】
二次函数的应用
(1)利用二次函数解决利润问题
在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.
(2)几何图形中的最值问题
几何图形中的二次函数问题常见的有:几何图形中面积的最值,用料的最佳方案以及动态几何中的最值的讨论.
(3)构建二次函数模型解决实际问题
利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.
【考点剖析】
利润问题
1.(2023秋•虹口区校级期末)某品牌裙子,平均每天可以售出20条,每条盈利40元,经市场调查发现,如果该品牌每条裙子每降价1元,那么平均每天可以多售出2条,那么当裙子降价 15 元时,可获得最大利润 1250 元.
分析:设每件裙子应降价x元,则每件盈利(40﹣x)元,平均每天的销售量为(20+2x)件,根据总利润=每件盈利×平均每天的销售量,即可得出关于x的二次函数关系式,再根据二次函数的性质可得答案.
【解答】解:设每件裙子应降价x元,则每件盈利(40﹣x)元,平均每天的销售量为(20+2x)件,
依题意得利润w=(40﹣x)(20+2x)=﹣2x2+60x+800=﹣2(x﹣15)2+1250.
所以当裙子降价15元时,可以获得最大利润为1250元,
故答案为:15,1250.
【点评】本题考查二次函数的应用,根据题意列出二次函数关系式是解题关键.
2.(2023春•嘉定区校级期中)某超市从厂家购进A、B两种型号的水杯,两次购进水杯的情况如表:
(1)求A、B两种型号的水杯进价各是多少元?
(2)在销售过程中,A型水杯因为物美价廉而更受消费者喜欢.为了增大B型水杯的销售量,超市决定对B型水杯进行降价销售,当销售价为44元时,每天可以售出20个,每降价1元,每天将多售出5个,请问超市应将B型水杯降价多少元时,每天售出B型水杯的利润达到最大?最大利润是多少?
分析:(1)设A种型号的水杯进价为x元,B种型号的水杯进价为y元,根据两次进货情况表,可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据:利润=(每台实际售价﹣每台进价)×销售量,列函数关系式,配方成二次函数的顶点式可得函数的最大值;
【解答】解:(1)设A种型号的水杯进价为x元,B种型号的水杯进价为y元,
根据题意得:100x+200y=8000200x+300y=13000,
解得:x=20y=30.
答:A种型号的水杯进价为20元,B种型号的水杯进价为30元;
(2)设超市应将B型水杯降价m元时,每天售出B型水杯的利润为W元,根据题意,
得:W=(44﹣m﹣30)(20+5m)
=﹣5m2+50m+280
=﹣5(m﹣5)2+405,
∴当m=5时,W取得最大值,最大值为405元,
答:超市应将B型水杯降价5元时,每天售出B型水杯的利润达到最大,最大利润为405元.
【点评】本题主要考查二元一次方程组及二次函数的实际应用,理解题意准确抓住相等关系,据此列出方程或函数关系式是解题的关键.
3.(2023春•徐汇区校级月考)某工厂设计了一款产品,成本为每件20元.投放市场进行试销,经调查发现,该种产品每天的销售量y(件)与销售单价x(元)之间满足一次函数的关系,其中20≤x≤40.
(1)根据表格求y关于x的函数解析式;
(2)设销售这种产品每天的利润为W(元),求W关于销售单价x之间的函数解析式并求当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
分析:(1)用待定系数法即可得y关于x的函数解析式;
(2)根据总利润=每件利润×销售量可列出W关于销售单价x的函数解析式,由二次函数性质可得答案.
【解答】解:(1)设一次函数的解析式为y=kx+b(k≠0),
把x=25、y=30;x=30、y=2代入y=kx+b得:
25k+b=3030k+b=20,解得k=−2b=80,
∴y关于x的函数解析式为y=﹣2x+80;
(2)根据题意得:
W=y(x﹣20)
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600
=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,W取最大值200,
答:W关于销售单价x的函数解析式为W==﹣2x2+120x﹣1600,当销售单价定为30元时,工厂每天获得的利润最大,最大利润是200元.
【点评】本题考查一次函数和二次函数的应用,涉及待定系数法,解题的关键是读懂题意,掌握总利润=每件利润×销售量列出W关于销售单价x的函数解析式.
4.(2023秋•奉贤区期中)某工厂生产一种火爆的网红电子产品,每件产品成本16元,工厂将该产品进行网络批发,批发单价y(元)与一次性批发量x(件)(x为正整数)之间满足如图所示的函数关系.
(1)直接写出y与x之间所满足的函数关系式,并写出自变量x的取值范围;
(2)若一次性批发量不低于20且不超过60件时,求获得的利润w与x的函数关系式,同时当批发量为多少件时,工厂获利最大?最大利润是多少?
分析:(1)认真观察图象,分别写出该定义域下的函数关系式,定义域取值全部是整数;
(2)根据利润=(售价﹣成本)×件数,列出利润的表达式,求出最值.
【解答】解:(1)当0<x≤20且x为整数时,y=40;
当20<x≤60且x为整数时,y=−12x+50;
当x>60且x为整数时,y=20;
(2)设所获利润w(元),
∴当20<x≤60且x为整数时,y=−12x+50,
∴w=(y﹣16)x=(−12x+50﹣16)x,
∴w=−12x2+34x,
∴w=−12(x﹣34)2+578,
∵−12<0,
∴当x=34时,w最大,最大值为578元.
答:一次批发34件时所获利润最大,最大利润是578元.
【点评】本题主要考查一次函数和二次函数的应用,根据题意列出函数表达式并熟练运用性质是解决问题的关键.
5.(2023秋•普陀区期中)某商店如果将进货为8元的商品按每件10元售出,每天可销售200件,通过一段时间的摸索,该店主发现这种商品每涨价0.5元,其销售量就减少10件,每降价0.5元,其销售量就增加10件.
(1)如果每天的利润要达到700元,售价应定为每件多少元?
(2)将售价定为每件多少元时,能使这天所获利润最大?最大利润是多少?
分析:(1)如果设每件商品提高x元,可先用x表示出单件的利润以及每天的销售量,然后根据总利润=单价利润×销售量列出关于x的方程,进而求出未知数的值.
(2)首先设应将售价提为x元时,才能使得所赚的利润最大为y元,根据题意可得:y=(x﹣8)[200﹣20(x﹣10)],然后化简配方,即可得y=﹣20(x﹣14)2+720,即可求得答案.
【解答】解:(1)设每件商品提高x元,
则每件利润为(10+x﹣8)=(x+2)元,
每天销售量为(200﹣20x)件,
依题意,得:(x+2)(200﹣20x)=700.
整理得:x2﹣8x+15=0.
解得:x1=3,x2=5.
∴把售价定为每件13元或15元能使每天利润达到700元;
若设每件商品降价x元,
则(2﹣x)(200+20x)=700.
整理得:x2+8x+15=0,
解得:x1=﹣3,x2=﹣5,
∴把售价定为每件13元或15元能使每天利润达到700元.
(2)设利润为y:
则y=(x﹣8)[200﹣20(x﹣10)]
=﹣20x2+560x﹣3200
=﹣20(x﹣14)2+720,
则当售价定为14元时,获得最大利润;最大利润为720元.
答:把售价定为每件13元或15元能使每天利润达到700元,将售价定位每件14元时,能使每天可获的利润最大,最大利润是720元.
【点评】此题考查的是二次函数在实际生活中的应用.此题难度不大,解题的关键是理解题意,找到等量关系,求得二次函数解析式.
最值问题
1.(2023秋•松江区期末)一位运动员投掷铅球,如果铅球运行时离地面的高度为y(米)关于水平距离x(米)的函数解析式为y=−112x2+23x+53,那么铅球运动过程中最高点离地面的距离为 3 米.
分析:直接利用配方法求出二次函数最值即可.
【解答】解:由题意可得:
y=−112x2+23x+53
=−112(x2﹣8x)+53
=−112(x﹣4)2+3,
故铅球运动过程中最高点离地面的距离为:3m.
故答案为:3.
【点评】此题主要考查了二次函数的应用,正确利用配方法求出最值是解题关键.
2.(2023秋•静安区校级月考)如图,一小孩将一只皮球从A处抛出去,它所经过的路线是某个二次函数图象的一部分,如果他的出手处A距地面的距离OA为1m,当球飞越的水平距离为8米时,球到达最高点B处,离地面高度为9米,则这个二次函数的表达式为 y=−18(x﹣8)2+9 ,小孩将球抛出了约 16.5 米(精确到0.1m).
分析:设出函数解析式的顶点式,把点A代入求得解析式,进一步求出与x轴交点坐标,即可解答.
【解答】解:根据题意知,抛物线的顶点B的坐标为(8,9),图象经过点A(0,1),
设抛物线的解析式为y=a(x﹣8)2+9,
把点A代入解析式得a=−18,
因此这个二次函数的表达式为 y=−18(x﹣8)2+9.
当y=0时,−18x2+2x+1=0,
解得x1≈16.5,x2=﹣0.5(不合题意,舍去);
因此小孩将球抛出了约16.5米.
故答案为:y=−18(x﹣8)2+9 、16.5.
【点评】此题考查二次函数的应用,解题的关键是利用顶点式求函数解析式,以及二次函数与一元二次方程的关系.
3.(2023秋•杨浦区校级期中)某建筑工程队在工地一边的靠墙处,用120米长的铁栅栏围成一个所占面积为长方形的临时仓库,其中墙仅80米长,铁栅栏只围三边,则所围仓库的最大面积为 1800 平方米.
分析:由题意得y=x(120﹣2x)=﹣2x(x﹣60),而120﹣2x≤80,即x≥20,根据函数的增减性即可求解.
【解答】解:设长方形的宽为x米,则平行于墙的一边为(120﹣2x)米,设围成仓库的面积为y平方米,
根据题意得y=x(120﹣2x)=﹣2x(x﹣60),
而120﹣2x≤80,即x≥20,
函数y的对称轴为x=30,
∵a=﹣2<0,故抛物线开口向下,当x<30时,y随x的增大而增大,
故当x=30(米)时,y有最大值,最大值为1800(平方米);
故所围仓库的最大面积为1800平方米,
故答案为1800.
【点评】本题考查的是二次函数的应用的运用,要注意靠墙的那面不需要栅栏,不要把平行于墙的一边算成是12(120﹣2x).
构建二次函数模型解决实际问题
1.(2023秋•虹口区期末)如图所示,一座抛物线形的拱桥在正常水位时,水面AB宽为20米,拱桥的最高点O到水面AB的距离为4米.如果此时水位上升3米就达到警戒水位CD,那么CD宽为( )
A.45米B.10米C.46米D.12米
分析:以O点为坐标原点,AB的垂直平分线为y轴,过O点作y轴的垂线,建立直角坐标系,设抛物线的解析式为y=ax2,由此可得A(﹣10,﹣4),B(10,﹣4),即可求函数解析式为y=−125x2,再将y=﹣1代入解析式,求出C、D点的横坐标即可求CD的长.
【解答】解:以O点为坐标原点,AB的垂直平分线为y轴,过O点作y轴的垂线,建立直角坐标系,
设抛物线的解析式为y=ax2,
∵O点到水面AB的距离为4米,
∴A、B点的纵坐标为﹣4,
∵水面AB宽为20米,
∴A(﹣10,﹣4),B(10,﹣4),
将A代入y=ax2,
﹣4=100a,
∴a=−125,
∴y=−125x2,
∵水位上升3米就达到警戒水位CD,
∴C点的纵坐标为﹣1,
∴﹣1=−125x2,
∴x=±5,
∴CD=10,
故选:B.
【点评】本题考查二次函数的应用,根据题意建立合适的直角坐标系,在该坐标系下求二次函数的解析式是解题的关键.
2.(2023•宝山区二模)有一座抛物线拱型桥,在正常水位时,水面BC的宽为10米,拱桥的最高点D到水面BC的距离DO为4米,点O是BC的中点,如图,以点O为原点,直线BC为x,建立平面直角坐标系xOy.
(1)求该抛物线的表达式;
(2)如果水面BC上升3米(即OA=3)至水面EF,点E在点F的左侧,求水面宽度EF的长.
分析:(1)直接假设出二次函数解析式进而得出答案;
(2)根据题意得出y=3进而求出x的值,即可得出答案.
【解答】解:(1)设抛物线解析式为:y=ax2+c,
由题意可得图象经过(5,0),(0,4),
则c=425a+4=0,
解得:a=−425,
故抛物线解析为:y=−425x2+4;
(2)由题意可得:y=3时,
3=−425x2+4
解得:x=±52,
故EF=5,
答:水面宽度EF的长为5m.
【点评】此题主要考查了二次函数的应用,正确得出函数解析式是解题关键.
四、二次函数与几何图形
1.(2023•宝山区模拟)在一块等腰直角三角形铁皮上截一块矩形铁皮.如图,已有的铁皮是等腰直角三角形ABC,它的底边AB长20厘米.要截得的矩形EFGD的边FG在AB上,顶点E、D分别在边CA、CB上.设EF的长为x厘米,矩形EFGD的面积为y平方厘米,试写出y关于x的函数解析式及定义域,并求当EF的长为4厘米时所截得的矩形的面积.
分析:由题意得,矩形的面积等于相邻两边之积,根据图中几何关系把ED边用x表示出来,再由矩形EFGD在等腰直角三角形内,求出定义域,最后把EF的长为4厘米,代入函数关系式,求得矩形面积.
【解答】解:∵△ABC是等腰直角三角形,四边形EFGD是矩形,
∴△AFE和△DGB都是等腰直角三角形,
∴AF=EF=x,GB=DG=x,
FG=AB﹣AF﹣GB=20﹣2x,
矩形EFGD的面积y=x(20﹣2x)
=﹣2x2+20x,
由0<20﹣2x<20,
解得0<x<10,
∴y关于x的函数关系式是y=﹣2x2+20x,
定义域是0<x<10,
当x=4时,y=﹣2×42+20×4=48,
即当EF的长为4厘米时,所截得的矩形的面积为48平方厘米.
【点评】此题考查等腰直角三角形和矩形的性质,在等腰直角三角形和矩形中解题,要注意几何关系.
2.(2023秋•浦东新区校级月考)将一条长20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这两段铁丝的长度分别为多少?
(2)两个正方形的面积之和可能等于12cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
(3)两个正方形的面积之和最小为 12.5 cm2.
分析:(1)这段铁丝被分成两段后,围成正方形.其中一个正方形的边长为xcm,则另一个正方形的边长为(5﹣x),根据“两个正方形的面积之和等于17cm2”作为相等关系列方程,解方程即可求解;
(2)设两个正方形的面积和为y,可得二次函数y=x2+(5﹣x)2=2(x−52)2+252,利用二次函数的最值的求法可求得y的最小值是12.5,所以可判断两个正方形的面积之和不可能等于12cm2;
(3)根据二次函数的性质即可得到答案.
【解答】解:(1)设其中一个正方形的边长为xcm,则另一个正方形的边长为(5﹣x)cm,
依题意列方程得x2+(5﹣x)2=17,
整理得:x2﹣5x+4=0,
(x﹣1)(x﹣4)=0,
解方程得x1=1,x2=4,
1×4=4,20﹣4=16;
因此这段铁丝剪成两段后的长度分别是4cm、16cm;
(2)两个正方形的面积之和不可能等于12cm2.理由:
设两个正方形的面积和为y,则
y=x2+(5﹣x)2=2(x−52)2+252,
∵a=2>0,
∴当x=52时,y的最小值=12.5>12,
∴两个正方形的面积之和不可能等于12cm2;
(3)设两个正方形的面积和为y,则
y=x2+(5﹣x)2=2(x−52)2+252,
∵a=2>0,
∴当x=52时,y的最小值=12.5cm2.
∴两个正方形的面积之和最小为12.5cm2.
故答案为:12.5.
【点评】此题考查了二次函数的应用,一元二次方程的应用,等量关系是:两个正方形的面积之和=17或12.读懂题意,找到等量关系准确地列出方程是解题的关键.
3.(2023秋•浦东新区校级月考)如图,在直角三角形ABC中,直角边AC=6cm,BC=8cm,设P,Q分别为AB,BC上的动点,点P自点A沿AB方向向点B作匀速移动且速度为每秒2cm,同时点Q自点B沿BC方向向点C作匀速移动且速度为每秒1cm.当P点到达B点时,Q点就停止移动,设P,Q移动的时间t秒.
(1)写出△PBQ的面积S(cm2)与时间t(s)之间的函数表达式,并写出t的取值范围.
(2)当t为何值时,△PBQ为等腰三角形?
分析:(1)过点P作PH⊥BC,垂足为H,从而得到△BPH∽△ABC,根据相似比例求出PH的长,可以得到用t表示面积的函数解析式;
(2)分三种情况讨论三角形PBQ为等腰三角形,即BP=BQ,BQ=PQ和BP=PQ,再分别求t的值.
【解答】解:(1)∵Rt△ABC中直角边AC=6,BC=8,
∴AB=62+82=10,
∴BP=10﹣2t,BQ=t.
如图1,过点P作PH⊥BC,垂足为H,
∵AC⊥BC,
∴△BPH∽△ABC,
∴ACPH=ABBP,即6PH=1010−2t,解得PH=6−65t,
∴S=12BQ•PH=12t•(6−65t)=−35t2+3t(0<t≤5);
(2)
①当BP=BQ时,10﹣2t=t,解得t=103秒;
②如图2,当BQ=PQ时,作QE⊥BD,垂足为E,
∵BQ=PQ,QE⊥BD,
∴BE=12BP=12(10﹣2t)=5﹣t,
∵∠B=∠B,∠ACB=∠QEB=90°,
∴△BQE∽△BAC,
∴BQAB=BEBC,即t10=5−t8,
解得t=259秒;
③如图3,当BP=PQ时,作PF⊥BC,垂足为F,
∵BP=PQ,PF⊥BC,
∴BF=12BQ=12t.
∵∠B=∠B,∠PFB=∠C=90°,
∴△BPF∽△BAC,
∴BPAB=BFBC,即10−2t10=t28,
解得t=8021秒.
∴当t=103秒,t=259秒,t=8021秒时,均使△PBQ为等腰三角形.
【点评】此题的是相似形综合题,涉及到相似三角形的判定与性质、等腰三角形的性质等知识,此类问题是近几年中考中较常见的题目,在解答时要注意进行分类讨论,不要漏解.
4.(2023春•金山区期末)如图,正方形ABCD,AB=4,点M是边BC的中点,点E是边AB上的一个动点,作EG⊥AM交AM于点G,EG的延长线交线段CD于点F.
(1)如图①,当点E与点B重合时,求证:BM=CF;
(2)设BE=x,梯形AEFD的面积为y,求y与x的函数解析式,并写出定义域.
分析:(1)证明△BAM≌△CBF(ASA)即可;
(2)按照(1)的思路,作EH⊥CD于H得:△BAM≌△即可求解.
【解答】(1)证明:∵GE⊥AM,∴∠BAM+∠ABG=90°,又∠CBF+∠ABG=90°,
在△BAM和△CBF中,∠BAM=∠CBF,AB=BC,∠ABM=∠BCF,
∴△BAM≌△CBF(ASA),∴BM=CF;
(2)作EH⊥CD于H,由(1)得:△BAM≌△HEF,
∴HF=BM=2,∴DF=4﹣2=x=2﹣x,
∴y=12×(4−x+2−x)×4=12−4x(0≤x<2),
答:y与x的函数解析式为∴y=12×(4−x+2−x)×4=12−4x(0≤x<2).
【点评】本题考查的是二次函数的应用,涉及到三角形全等的知识,此类题目通常(1)为(2)提供思路.
5.(2023春•长宁区期末)已知在等腰梯形ABCD中,AD∥BC,AD=AB=CD=6厘米,∠B=60°,点P在边AD上以每秒2厘米的速度从D出发,向点A运动;点Q在边AB上以每秒1厘米的速度从点B出发,向点A运动.已知P、Q两点同时出发,当其中一个点到达终点时,另外一个点也随之停止运动,设两个点的运动时间为t秒,联结PC、QD.
(1)如图1,若四边形BQDC的面积为S平方厘米,求S关于t的函数解析式并写出函数定义域;
(2)若PC与QD相交于点E,且∠PEQ=60°,求t的值.
分析:(1)由S四边形BQDC=S梯形ABCD﹣SADQ即可求出表达式;(2)当且∠PEQ=60°时,可证△CDP≌△ADQ,则PD=AQ,即可求解.
【解答】
(1)过点A作AH⊥BC,垂足为H,过点D作DF⊥AB,垂足为F,
在Rt△ABH中,∠B=60°,AB=6,可得:AH=33、DF=33,
S四边形BQDC=S梯形ABCD﹣SADQ=273−(93−323t)=183+323t(0<t≤3);
答:求S关于t的函数解析式为S=183+323t(0<t≤3);
(2)当且∠PEQ=60°时,可证△CDP≌△ADQ(AAS),
∴PD=AQ,即:6﹣t=2t,t=2.
答:t的值为2.
【点评】本题考查的是二次函数的应用,(1)中S四边形BQDC=S梯形ABCD﹣SADQ这种面积拆分的办法是此类题目常用的方法.
【过关检测】
1.(2023·上海九年级专题练习)如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.
(1)当矩形DEFG是正方形时,求正方形的边长.
(2)设EF=x,矩形DEFG的面积为S,求S关于x的函数关系式,当x为何值时S有最大值,并求出最大值.
答案:(1);(2),当x=4时,S有最大值20
分析:(1)GF∥BC得△AGF∽△ABC,利用相似三角形对应边上高的比等于相似比,列方程求解;
(2)根据相似三角形的性质求出GF=10−x,求出矩形的面积,运用二次函数性质解决问题.
【详解】
(1)设HK=y,则AK=AH﹣KH=AH﹣EF=8﹣y,
∵四边形DEFG为矩形,
∴GF∥BC,
∴△AGF∽△ABC,
∴AK:AH=GF:BC,
∵当矩形DEFG是正方形时,GF=KH=y,
∴(8﹣y):8=y:10,
解得:y=;
(2)设EF=x,则KH=x.
∴AK=AH﹣EF=8﹣x,
由(1)可知:,
解得:GF=10﹣x,
∴s=GF•EF=(10﹣x)x=﹣(x﹣4)2+20,
∴当x=4时S有最大值,并求出最大值20.
【点睛】本题考查了相似三角形的性质,二次函数的最值,矩形的性质的应用,注意:矩形的对边相等且平行,相似三角形的对应高的比等于相似比,题目是一道中等题,难度适中.
2.(2023·上海九年级专题练习)商场购进某种新商品在试销期间发现,当每件利润为10元时,每天可销售70件;当每件商品每涨价1元,日销售量就减少1件,但每天的销售量不得低于35件.据此规律,请回答下列问题.
(1)设每件涨了x元时,每件盈利_________元,商品每天可销售______件;
(2)在商品销售正常的情况下,每件商品涨价多少元时,商场每天盈利为1500元?
(3)若商场的每天盈利能达到最大,请直接写出每天的最大盈利为______________.
答案:(1),;(2)20;(3)1600
分析:(1)用售价减去进价即可求得每件利润;销售量等于原来销售量减去减少的销售量即可;
(2)利用总利润=单件利润×销量列出方程求解即可;
(3)配方后即可确定最大利润;
【详解】解:(1)设每件涨了x元时,每件盈利(10+x)元,商品每天可销售(70-x)件;
(2)根据题意得:(10+x)(70-x)=1500,
解得:x=20或x=40(不合题意,舍去),
答:每件商品涨20元时商场每天盈利可达1500元.
(3)设总利润为w元,则w=(10+x)(70-x)=-(x-30)2+1600,
∴总利润的最大值为1600元.
【点睛】本题考查了一元二次方程的应用及二次函数的应用,解题的关键是能够根据题意列出方程或二次函数,渗透了数学建模的数学思想.
3.(2023·上海九年级专题练习)某电动机加工厂以400元/个的价格新接了一批电动机加工业务.根据工厂以往的制造能力,该工厂每天制造电动机的数量为x(个)(200≤x≤500),且每个电动机的制造成本y(元)与每天制造电动机的数量x(个)之间的函数关系的图象如图所示.
(1)求y与x之间的函数表达式;
(2)已知该工厂每天各项消耗的费用是2万元,每天的利润为w元,请求出w与x之间的函数表达式,并求出当x为多少时,w最大,最大日利润是多少.
答案:(1)y=-x+500;(2)w=(x-100)2-25000;当x=500时,w最大,最大日利润为55000元.
分析:(1)设函数表达式为y=kx+b,把(200,400),(500,250)分别代入即可求解;
(2)根据题意可求得w与x的函数关系式:w=(400-y)x-20000=[400-(-x+500)]x-20000=(x-100)2-25 000,根据二次函数的性质可知,当x>100时,w随x的增大而增大,再结合200≤x≤500,可知当x=500时,w取得最大值,代入计算即可.
【详解】解:(1)根据题意,设y=kx+b,
将(200,400),(500,250)分别代入,
得,
解得,
故y与x之间的函数表达式为y=-x+500;
(2)根据题意,得w=(400-y)x-20000=[400-(-x+500)]x-20 000=(x-100)2-25 000,
∵>0,
∴当x>100时,w随x的增大而增大,
又∵200≤x≤500,
∴当x=500时,w取得最大值,最大值为×(500-100)2-25000=55000,
答:当x=500时,w最大,最大日利润为55000元.
【点睛】本题考查了二次函数的实际应用,理清题中的数量关系并熟练掌握二次函数的性质是解题的关键.
4.(2023秋•浦东新区月考)阅读材料:
配方法可以用来解一元二次方程,还可以用它来解决一些最值问题,比如:因为3a2≥0,所以3a2+1就有个最小值1,即3a2+1≥1,只有当a=0时,才能得到这个式子的最小值1.同样,因为﹣3a2≤0,所以﹣3a2+1有最大值1,即﹣3a2+1≤1,只有在a=0时,才能得到这个式子的最大值1.
请解决下列问题:
(1)当x= 2 时,代数式3(x﹣2)2﹣1有最 小 (填“大”或“小”)值为 ﹣1 ;
(2)当x= ﹣1 时,代数式﹣2x2﹣4x+3有最 大 (填“大”或“小”)值为 5 ;
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度16m,求:当花园与墙相邻(即垂直于墙)的边长为多少时,花园的面积最大?最大面积是多少?
分析:(1)根据阅读材料即可求解;
(2)根据阅读材料即可求解;
(3)根据矩形面积公式列出二次函数解析式,再根据二次函数的性质即可求解.
【解答】解:(1)当x=2时,代数式3(x﹣2)2﹣1有最小值为﹣1;
故答案为2、小、﹣1.
(2)代数式﹣2x2﹣4x+3=﹣2(x+1)2+5
∴当x=﹣1时,代数式﹣2x2﹣4x+3有最大值为5.
故答案为﹣1、大、5.
(3)设花园与墙相邻(即垂直于墙)的边长为xm,花园的面积为ym2.根据题意,得
y=x(16﹣2x)
=﹣2x2+16x
=﹣2(x﹣4)2+32
∵﹣2<0,∴当x=4时,y有最大值为32,
答:花园与墙相邻(即垂直于墙)的边长为4m时,花园的面积最大,最大面积是32m2.
【点评】本题考查了二次函数的应用,解决本题的关键是理解最值.
进货批次
A型水杯(个)
B型水杯(个)
总费用(元)
一
100
200
8000
二
200
300
13000
销售量y(件)
…
30
20
10
…
销售单价x(元)
…
25
30
35
…
相关试卷
这是一份沪教版暑假新九年级数学考点讲与练第21讲二次函数中面积的存在性问题(考点讲与练)(原卷版+解析),共40页。
这是一份沪教版暑假新九年级数学考点讲与练第20讲二次函数中梯形的存在性问题(考点讲与练)(原卷版+解析),共25页。
这是一份沪教版暑假新九年级数学考点讲与练第16讲二次函数中的角相等问题(考点讲与练)(原卷版+解析),共29页。









