




- 考点16特殊三角形(等腰三角形与直角三角形)(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点16特殊三角形(等腰三角形与直角三角形)(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点17多边形与平行四边形(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点18特殊的平行四边形(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
- 考点18特殊的平行四边形(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版 试卷 0 次下载
考点17多边形与平行四边形(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版
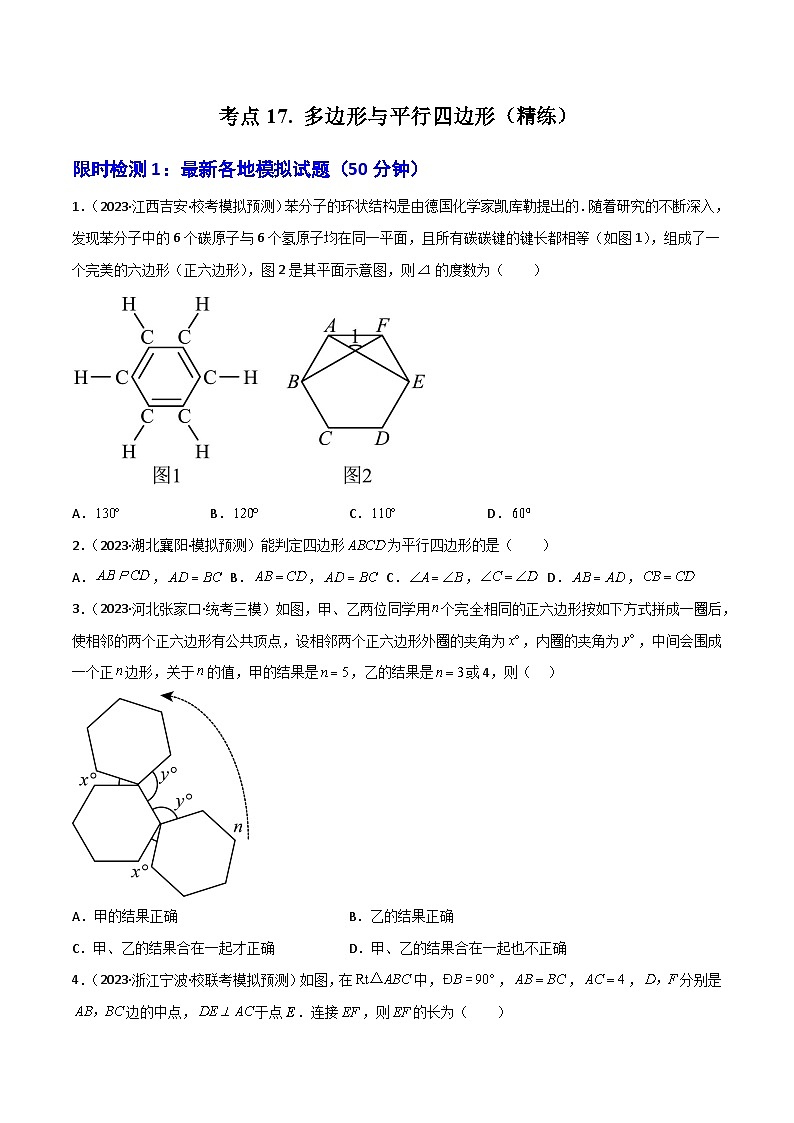
展开1.(2023·江西吉安·校考模拟预测)苯分子的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子与6个氢原子均在同一平面,且所有碳碳键的键长都相等(如图1),组成了一个完美的六边形(正六边形),图2是其平面示意图,则的度数为( )
A.B.C.D.
2.(2023·湖北襄阳·模拟预测)能判定四边形为平行四边形的是( )
A., B., C., D.,
3.(2023·河北张家口·统考三模)如图,甲、乙两位同学用个完全相同的正六边形按如下方式拼成一圈后,使相邻的两个正六边形有公共顶点,设相邻两个正六边形外圈的夹角为,内圈的夹角为,中间会围成一个正边形,关于的值,甲的结果是,乙的结果是或4,则( )
A.甲的结果正确B.乙的结果正确
C.甲、乙的结果合在一起才正确D.甲、乙的结果合在一起也不正确
4.(2023·浙江宁波·校联考模拟预测)如图,在中,,,,分别是边的中点,于点.连接,则的长为( )
A.B.C.D.
5.(2023·广东·统考二模)如图,在中,平分,交于点F,平分交于点E,,则长为( )
A.1B.2C.3D.4
6.(2023·浙江·模拟预测)在平行四边形中,点是的中点,与交于点,则与四边形的面积之比是( )
A.B.C.D.
7.(2023·广东·中考模拟预测)如图,在中,一定正确的是( )
A.B.C.D.
8.(2023·重庆·中考模拟预测)如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形,其中一张纸条在转动过程中,下列结论一定成立的是( )
A.四边形周长不变 B. C.四边形面积不变 D.
9.(2023·浙江绍兴·校联考三模)淇淇用图一的六个全等纸片拼接图2所示的外轮廓是正六边形,如果用若干个纸片按照图3所示的方法拼接成外轮廓是正n变形图案,那么的值为 .
10.(2023·湖北孝感·模拟预测)已知,正多边形的每个内角为,则这个多边形的对角线共有 条.
11.(2023·河北·模拟预测)一个多边形,除了一个内角外,其余各角的和为,则这一内角为 度.
12.(2022·黑龙江哈尔滨·哈尔滨市萧红中学校考一模)四边形是平行四边形,,的平分线交直线于点,若,则四边形的周长为 .
13.(2022·黑龙江哈尔滨·校考一模)如图,在中,E,F分别是,的中点,,,且,则的长是 .
14.(2023·福建·一模)如图,在平行四动形纸板中,点分别为的中点,连接.将一飞镖随机投掷到平行四边形纸板上,则飞镖落在阴影部分的概率为 .
15.(2022·广东·模拟预测)如图,是的弦,,点是上的一个动点,且,若点,分别为,的中点,则线段长度的最大值为 .
16.(2022·黑龙江·校考模拟预测)在平行四边形中,,,边上的高为4,则平行四边形周长等于 .
17.(2024·重庆·中考模拟预测)如图,在正六边形中,,是对角线上的两点,添加下列条件中的一个:①;②;③;④.能使四边形是平行四边形的是__________(填上所有符合要求的条件的序号).
18.(2023·广东佛山·统考模拟预测)如图,四边形中,,,,是边的中点,连接并延长与的延长线相交于点.
(1)求证:四边形是平行四边形;(2)若是等腰三角形,求四边形的面积.
19.(2023·陕西宝鸡·校考一模)问题提出:
如图,在中,.若,则的值为__________.
问题探究:如图,在四边形中,对角线、相交于点,、、、分别为、、、的中点,连接、、、.若,求四边形的面积.
问题解决:如图,某市有一块五边形空地,其中米,米,米,米,现计划在五边形空地内部修建一个四边形花园,使点、、、分别在边、、、上,要求请问,是否存在符合设计要求的面积最大的四边形花园?若存在,求四边形面积的最大值;若不存在,请说明理由.
20.(2023·山东·二模)(问题)用边形的对角线把边形分割成(个三角形,共有多少种不同的分割方案?
(探究)为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有种.
探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?如图①,图②,显然,只有2种不同的分割方案.所以,.
探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?不妨把分割方案分成三类:
第1类:如图③,用点,与连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有种不同的分割方案,所以,此类共有种不同的分割方案.
第2类:如图④,用点,与连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为种分割方案.
第3类:如图⑤,用点,与连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有f(4)种不同的分割方案,所以,此类共有f(4)种不同的分割方案.
所以,(种)
探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?不妨把分割方案分成四类:
第1类:如图⑥,用,与连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有种不同的分割方案,所以,此类共有种不同的分割方案.
第2类:如图⑦,用,与连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有种不同的分割方案.所以,此类共有种分割方案.
第3类:如图⑧,用,与连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有种不同的分割方案.所以,此类共有种分割方案.
第4类:如图,用,与连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有种不同的分割方案.所以,此类共有种分割方案.
所以,
(种)
探究四:用七边形的对角线把七边形分割成5个三角形,则与的关系为,共有______种不同的分割方案.……
(结论)用边形的对角线把边形分割成个三角形,共有多少种不同的分割方案?(直接写出与之间的关系式,不写解答过程)
(应用)用九边形的对角线把九边形分割成7个三角形,共有多少种不同的分割方案?(应用上述结论中的关系式求解)
限时检测2:最新各地中考真题(50分钟)
1.(2023·湖南益阳·统考中考真题)如图,的对角线交于点,下列结论一定成立的是( )
A.B.C. D.
2.(2023·内蒙古赤峰·统考中考真题)如图,在中,,,.点F是中点,连接,把线段沿射线方向平移到,点D在上.则线段在平移过程中扫过区域形成的四边形的周长和面积分别是( )
A.16,6B.18,18C.16.12D.12,16
3.(2023·河北·统考中考真题)综合实践课上,嘉嘉画出,利用尺规作图找一点C,使得四边形为平行四边形.图1~图3是其作图过程.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等 C.对角线互相平分 D.一组对边平行且相等
4.(2023·山西·统考中考真题)蜂巢结构精巧,其巢房横截面的形状均为正六边形.如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点均为正六边形的顶点.若点的坐标分别为,则点的坐标为( )
A.B.C.D.
5.(2023·四川自贡·统考中考真题)第29届自贡国际恐龙灯会“辉煌新时代”主题灯组上有一幅不完整的正多边形图案,小华量得图中一边与对角线的夹角,算出这个正多边形的边数是( )
A.9B.10C.11D.12
6.(2023·浙江湖州·统考中考真题)如图,已知,以点O为圆心,适当长为半径作圆弧,与角的两边分别交于C,D两点,分别以点C,D为圆心,大于长为半径作圆弧,两条圆弧交于内一点P,连接,过点P作直线,交OB于点E,过点P作直线,交于点F.若,,则四边形的面积是( )
A.B.C.D.
7.(2022·河北·中考真题)依据所标数据,下列一定为平行四边形的是( )
A.B.C.D.
8.(2023·湖北黄石·统考中考真题)如图,在中,按以下步骤作图:①分别以点B,C为圆心,大于的长为半径画弧,两弧相交于E,F两点,和交于点O;②以点A为圆心,长为半径画弧,交于点D;③分别以点D,C为圆心,大于的长为半径画弧,两弧相交于点M﹐连接和交于点N,连接若,则的长为( )
A.2B.C.4D.
9.(2023·浙江金华·统考中考真题)如图,把两根钢条的一个端点连在一起,点分别是的中点.若,则该工件内槽宽的长为 .
10.(2023·四川遂宁·统考中考真题)如图,中,为对角线,分别以点A、B为圆心,以大于的长为半径画弧,两弧相交于点M、N,作直线交于点E,交于点F,若,,,则的长为 .
11.(2023·四川凉山·统考中考真题)如图,的顶点的坐标分别是.则顶点的坐标是 .
12.(2023·新疆·统考中考真题)如图,在中,,,,点是上一动点,将沿折叠得到,当点恰好落在上时,的长为 .
13.(2022·江苏连云港·中考真题)如图,在中,.利用尺规在、上分别截取、,使;分别以、为圆心,大于的长为半径作弧,两弧在内交于点;作射线交于点.若,则的长为_________.
14.(2021·江苏泰州市·中考真题)如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 ___.
15.(2023·浙江湖州·统考中考真题)如图,在中,,于点D,点E为AB的中点,连结DE.已知,,求BD,DE的长.
16.(2023·重庆·统考中考真题)学习了平行四边形后,小虹进行了拓展性研究.她发现,如果作平行四边形一条对角线的垂直平分线,那么这个平行四边形的一组对边截垂直平分线所得的线段被垂足平分. 她的解决思路是通过证明对应线段所在的两个三角形全等得出结论.请根据她的思路完成以下作图与填空:
用直尺和圆规,作的垂直平分线交于点E,交于点F,垂足为点O.(只保留作图痕迹)
已知:如图,四边形是平行四边形,是对角线,垂直平分,垂足为点O.
求证:.
证明:∵四边形是平行四边形,
∴.∴ ① .
∵垂直平分,∴ ② .
又___________③ .
∴.∴.
小虹再进一步研究发现,过平行四边形对角线中点的直线与平行四边形一组对边相交形成的线段均有此特征.请你依照题意完成下面命题:
过平行四边形对角线中点的直线 ④ .
17.(2023·浙江台州·统考中考真题)如图,点在线段上(点C在点之间),分别以为边向同侧作等边三角形与等边三角形,边长分别为.与交于点H,延长交于点G,长为c.
(1)若四边形的周长与的周长相等,则之间的等量关系为 .
(2)若四边形的面积与的面积相等,则a,b,c之间的等量关系为 .
18.(2023·江苏扬州·统考中考真题)如图,点E、F、G、H分别是各边的中点,连接相交于点M,连接相交于点N.(1)求证:四边形是平行四边形;(2)若的面积为4,求的面积.
19.(2023·浙江绍兴·统考中考真题)在平行四边形中(顶点按逆时针方向排列),为锐角,且.(1)如图1,求边上的高的长.
(2)是边上的一动点,点同时绕点按逆时针方向旋转得点.
①如图2,当点落在射线上时,求的长.②当是直角三角形时,求的长.
20.(2023·黑龙江·统考中考真题)如图①,和是等边三角形,连接,点F,G,H分别是和的中点,连接.易证:.
若和都是等腰直角三角形,且,如图②:若和都是等腰三角形,且,如图③:其他条件不变,判断和之间的数量关系,写出你的猜想,并利用图②或图③进行证明.
(1)作的垂直平分线交于点O;
(2)连接,在的延长线上截取;
(3)连接,,则四边形即为所求.
考点21与圆有关的计算(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版: 这是一份考点21与圆有关的计算(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点21与圆有关的计算精练原卷版-2024年中考数学一轮复习之核心考点精讲精练全国通用docx、考点21与圆有关的计算精练解析版docx等2份试卷配套教学资源,其中试卷共47页, 欢迎下载使用。
考点18特殊的平行四边形(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版: 这是一份考点18特殊的平行四边形(精练)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点18特殊的平行四边形精练-2024年中考数学一轮复习之核心考点精讲精练全国通用原卷版docx、考点18特殊的平行四边形精练解析版docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。
考点17多边形与平行四边形(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版: 这是一份考点17多边形与平行四边形(精讲)-2024年中考数学一轮复习之核心考点精讲精练(全国通用)原卷版+解析版,文件包含考点17多边形与平行四边形精讲-2024年中考数学一轮复习之核心考点精讲精练全国通用原卷版docx、考点17多边形与平行四边形精讲-2024年中考数学一轮复习之核心考点精讲精练全国通用解析版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。












