湖南省长沙市2023-2024学年高一上需求入学暨分班试卷数学模拟练习

这是一份湖南省长沙市2023-2024学年高一上需求入学暨分班试卷数学模拟练习，共10页。试卷主要包含了定义等内容，欢迎下载使用。

一､选择题：本题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.
1.1. 已知 a 是 13 的小数部分,则 aa+6 的值为
A. 13 B. 4
C. 4-13 D. 313-6
2. 如果一个多边形的内角和是它外角和的 4 倍, 那么这个多边形的边数为
A. 6 B. 8 C. 9 D. 10
3.已知点在第二象限，则的取值范围在数轴上表示正确的是（ ）
A.B.
C.D.
4.如果外切的两圆和的半径分别为2和4，则半径为6，且与和都相切的圆有（ ）
A.4个B.5个C.6个D.7个
5.是2022个由1和组成的数，，则（ ）
A.2021B.4042C.3640D.4842
6.某餐厅为了追求时间效率，推出一种液体“沙漏”免单方案（即点单完成后，开始倒转“沙漏”，“沙漏”漏完前，客人所点菜需全部上桌，否则该桌免费用餐）.“沙漏"是由一个圆锥体和一个圆柱体相通连接而成.某次计时前如图（1）所示，已知圆锥体底面半径是，高是；圆柱体底面半径是，液体高是.计时结束后如图（2）所示，求此时“沙漏"中液体的高度为（ ）
A.B.C.D.
7.如果不等式组4x-a≥03x-b<0的整数解仅为1，2，3，那么适合这个不等式组的整数a、b的组合情况a,b共有（ ）种．
A．12B．7C．9D．16
8.定义：平面直角坐标系中，点的横坐标的绝对值表示为，纵坐标的绝对值表示为，我们把点的横坐标与纵坐标的绝对值之和叫做点的折线距离，记为（其中的“+”是四则运算中的加法）.若拋物线与直线只有一个交点，已知点在第一象限，且，令，则的取值范围为（ ）
A.B.
C.D.
二､填空题：本题共4小题，每小题4分，共16分.
9. 设点 Px,y 在第二象限内,且 x=3,y=2 ,则点 P 关于原点的对称点为___.
10.若关于 x 的分式方程 xx-2+2m2-x=2m 无解,则的值为___________.
11.正比例函数与反比例函数的图像相交于两点，已知点的横坐标为1，当时，的取值范围是___________.
12.如图，中，，点在线段上，以为圆心，长为半径的圆与边相交于另一点，点在直线上，且是的切线，则的最小值为___________.
三､解答题：本题共4小题，共52分.应写出文字说明､证明过程或演算步骤.
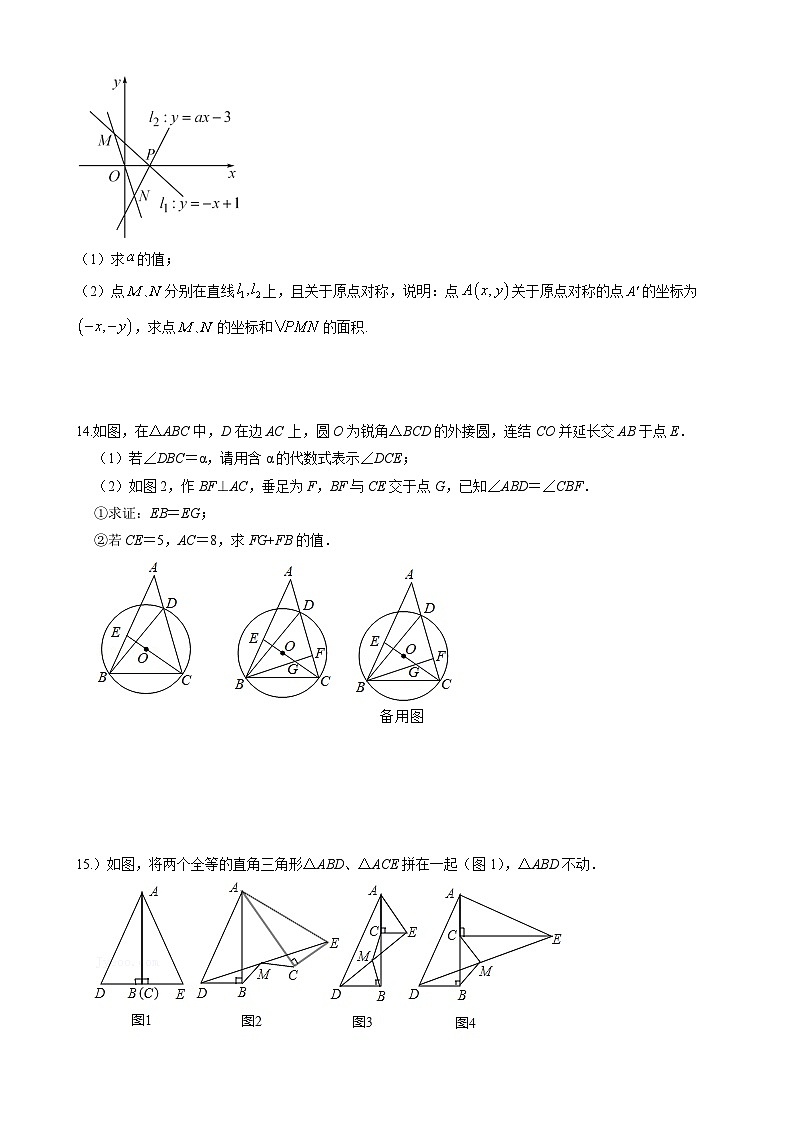
13.如图，在同一坐标系中，直线交轴于点，直线过点.
（1）求的值；
（2）点分别在直线上，且关于原点对称，说明：点关于原点对称的点的坐标为，求点的坐标和的面积.
14.如图，在△ABC中，D在边AC上，圆O为锐角△BCD的外接圆，连结CO并延长交AB于点E．
（1）若∠DBC＝α，请用含α的代数式表示∠DCE；
（2）如图2，作BF⊥AC，垂足为F，BF与CE交于点G，已知∠ABD＝∠CBF．
①求证：EB＝EG；
②若CE＝5，AC＝8，求FG+FB的值．
15.）如图，将两个全等的直角三角形△ABD、△ACE拼在一起（图1），△ABD不动．
（1）若将△ACE绕点A逆时针旋转，连接DE，M是DE的中点，连接MB、MC（图2），证明：MB＝MC．
（2）若将图1中的CE向上平移，∠CAE不变，连接DE，M是DE的中点，连接MB、MC（图3），判断并直接写出MB、MC的数量关系．
（3）在（2）中，若∠CAE的大小改变（图4），其他条件不变，则（2）中的MB、MC的数量关系还成立吗？说明理由．
16.在平面直角坐标系中，抛物线与轴分别相交于两点（点在点的左侧），与轴相交于点，设抛物线的对称轴与轴相交于点，且.
（1）求的值；
（2）将抛物线向上平移3个单位，得到抛物线，设点是抛物线上在第一象限内不同的两点，射线分别交直线于点，设的横坐标分别为，且，求证：直线经过定点.
常考答案
一､选择题：本题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.
1. 【答案】：B
2 【答案】D.
3. 【答案】C
4. 【答案】B
5 【答案】C
6. 【答案】B
7 【答案】A．
8. 【答案】C
二､填空题：本题共4小题，每小题4分，共16分.
9.
【答案】(3,-2)
10.
【答案】的值为或1/2
11.
【答案】或
12.
【答案】4.8
三､解答题：本题共4小题，共52分.应写出文字说明､证明过程或演算步骤.
13.
【答案】（1）
（2），
【解析】
【分析】（1）由直线求出点的坐标，再将点的坐标代入方程中可求出的值；
（2）由题意设 ，则，再将点的坐标代入直线中可求出，从而可求得两点的坐标，进而可求出的面积.
【小问1详解】
对于直线，当时，，
所以
因为直线过点，
所以，得，
【小问2详解】
由得，
设 ，则.
又在上，
所以，解得，
则
所以.
14.
【答案】【分析】（1）根据圆周角定理即可解决问题；
（2）①结合（1）利用三角形内角和定理即可解决问题；
②作EM⊥BE，EN⊥AC，证明四边形EMFN为矩形，再根据线段的和差即可解决问题．
【解答】（1）解：如图，连结OD，
∵∠DOC＝2∠DBC＝2α，
又∵OD＝OC，
∴∠DCE＝90°﹣α；
（2）①证明：∵∠ABD＝∠CBF，
∴∠EBG＝∠ABD+∠DBF＝∠CBF+∠DBF＝∠DBC，
设∠DBC＝α，
由（1）得：∠DCE＝90°﹣α，
∵BF⊥AC，
∴∠FGC＝∠BGE＝α，
∴∠EBG＝∠EGB，
∴EB＝EG；
②解：如图，作EM⊥BE，EN⊥AC，
由①得：∠EBG＝α，∠ACE＝90°﹣α，
∵BF⊥AC
∴∠A＝90°﹣α，
∴AE＝CE＝5，
∵EN⊥AC，AC＝8，
∴CN＝4，
∴EN＝3，
∵EM⊥BF，NF⊥BF，EN⊥AC，
∴四边形EMFN为矩形，
∴EN＝MF＝3，
∵EB＝EG，EM⊥BG，
∴BM＝GM，
∴FG+FB＝FM﹣MG+FM+BM＝2FM＝6．
15.
【分析】（1）连接AM，根据全等三角形的对应边相等可得AD＝AE，AB＝AC，全等三角形对应角相等可得∠BAD＝∠CAE，再根据等腰三角形三线合一的性质得到∠MAD＝∠MAE，然后利用“边角边”证明△ABM和△ACM全等，根据全等三角形对应边相等即可得证；
（2）延长DB、AE相交于E′，延长EC交AD于F，根据等腰三角形三线合一的性质得到BD＝BE′，然后求出MB∥AE′，再根据两直线平行，内错角相等求出∠MBC＝∠CAE，同理求出MC∥AD，根据两直线平行，同位角相等求出∠BCM＝∠BAD，然后求出∠MBC＝∠BCM，再根据等角对等边即可得证；
（3）延长BM交CE于F，根据两直线平行，内错角相等可得∠MDB＝∠MEF，∠MBD＝∠MFE，然后利用“角角边”证明△MDB和△MEF全等，根据全等三角形对应边相等可得MB＝MF，然后根据直角三角形斜边上的中线等于斜边的一半证明即可．
【解答】证明：（1）如图2，连接AM，由已知得△ABD≌△ACE，
∴AD＝AE，AB＝AC，∠BAD＝∠CAE，
∵MD＝ME，
∴∠MAD＝∠MAE，
∴∠MAD﹣∠BAD＝∠MAE﹣∠CAE，
即∠BAM＝∠CAM，
在△ABM和△ACM中，AB=AC∠BAM=∠CAMAM=AM，
∴△ABM≌△ACM（SAS），
∴MB＝MC；
（2）MB＝MC．
理由如下：如图3，延长DB、AE相交于E′，延长EC交AD于F，
∴BD＝BE′，CE＝CF，
∵M是ED的中点，B是DE′的中点，
∴MB∥AE′，
∴∠MBC＝∠CAE，
同理：MC∥AD，
∴∠BCM＝∠BAD，
∵∠BAD＝∠CAE，
∴∠MBC＝∠BCM，
∴MB＝MC；
解法二：如图3中，延长CM交BD于点T．
∵EC∥DT，
∴∠CEM＝∠TDM，
在△ECM和△DTM中，
∠CEM=∠TDMEM=DM∠EMC=∠DMT，
∴△ECM≌△DTM（ASA），
∴CM＝MT，
∵∠CBT＝90°，
∴BM＝CM＝MT．
（3）MB＝MC还成立．
如图4，延长BM交CE于F，
∵CE∥BD，
∴∠MDB＝∠MEF，∠MBD＝∠MFE，
又∵M是DE的中点，
∴MD＝ME，
在△MDB和△MEF中，
∠MDB=∠MEF∠MBD=∠MFEMD=ME，
∴△MDB≌△MEF（AAS），
∴MB＝MF，
∵∠ACE＝90°，
∴∠BCF＝90°，
∴MB＝MC．
16.
【答案】（1）；
（2）证明见解析
【解析】
【分析】（1）由顶点式求得对称轴，由处函数值求得点坐标，根据列方程求解即可；
（2）设点，结合原点可得直线的解析式，再由可得点横坐标，由可得；设直线的解析式为，与联立之后可得，，代入求得，继而求出答案
【小问1详解】
解：依题意得：，
抛物线的对称轴为直线，
，
在中，令，则，
，，
，，解得；
【小问2详解】
将代入抛物线得，
如图，将抛物线向上平移3个单位后得到拋物线，
点是拋物线上在第一象限内不同的两点，
设点，
由分别可求得：
点在直线上，
点，
，即，
整理得，
设直线的解析式为，与联立得：
，
整理得，
由根与系数的关系可得：，
，，
，
直线的解析式为，
当时，，
直线经过定点