福建省泉州市晋江市2023-2024学年八年级下学期期末数学试题

这是一份福建省泉州市晋江市2023-2024学年八年级下学期期末数学试题，共11页。试卷主要包含了07，0000004米，则0等内容，欢迎下载使用。

（本卷共8页，25道题．满分150分；考试时间120分钟）
友情提示：所有答案必须填写到答题卡相应的位置上
学校________ 姓名________ 考生号________
一、选择题：本题共10小题，每小题4分，共40分。在每小题给出的四个选项中，只有一项是符合要求的。
1．化简的结果是
A．a B． C． D．
2．据报道，流行性感冒病毒简称流感病毒，丝状流感病毒的长度可达0.0000004米，则0.0000004用科学记数法可表示为
A． B． C． D．
3．在平面直角坐标系xOy中，已知点A（3，2）与点B（3，），下列说法正确的是
A．轴 B．轴 C． D．
4．下列四边形中，是中心对称图形而不是轴对称图形的是
A．平行四边形 B．矩形 C．菱形 D．正方形
5．在平面直角坐标系xOy中，一次函数的图象与x轴的交点坐标为
A．（0，4） B．（2，0） C．（，0） D．（0，2）
6．要说明“四个角是直角的四边形是正方形”是假命题，可作为反例的图形是
A．平行四边形 B．矩形 C．菱形 D．正方形
7．对于正比例函数，下列说法正确的是
A．函数的图象从左到右呈上升趋势
B．函数的图象经过第一、三象限
C．函数的图象与y轴正半轴的夹角为
D．图象向上平移2个单位后的表达式为
8．如图，将矩形ABCD（）按如图所示步骤进行折叠及剪裁，若将完全展开后，则所得到的图形一定是
A．等腰三角形 B．等边三角形 C．菱形 D．矩形
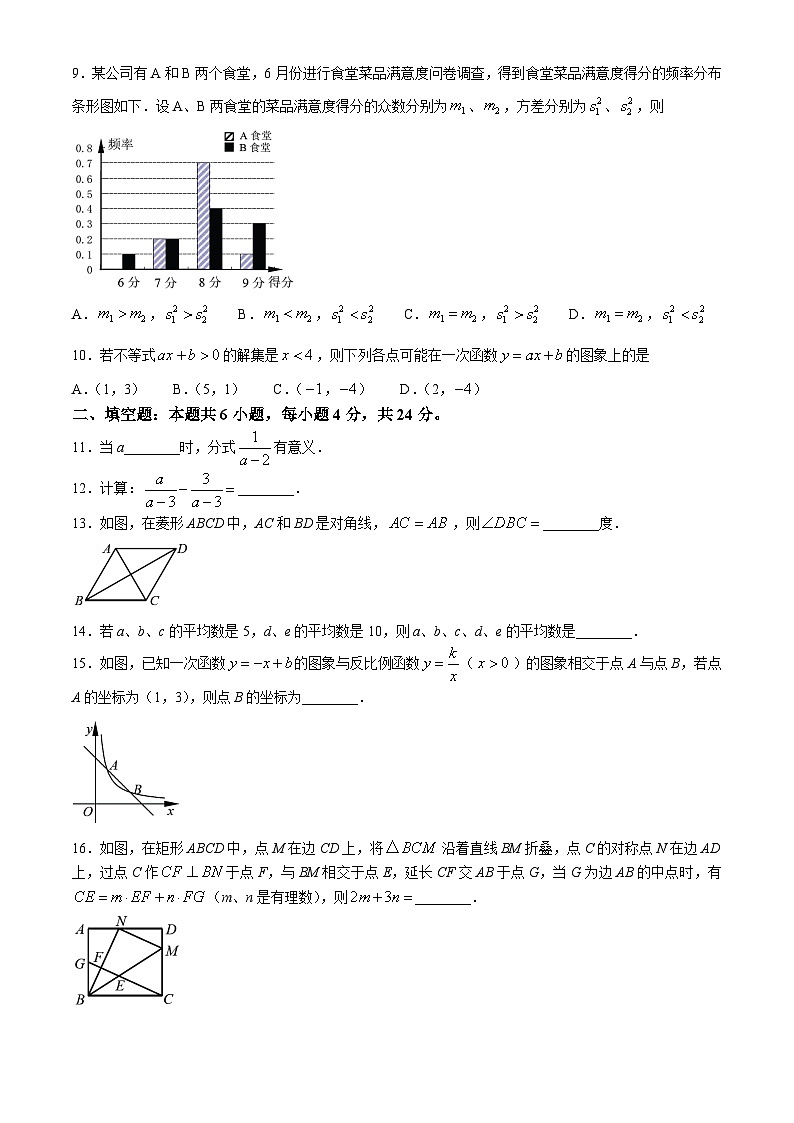
9．某公司有A和B两个食堂，6月份进行食堂菜品满意度问卷调查，得到食堂菜品满意度得分的频率分布条形图如下．设A、B两食堂的菜品满意度得分的众数分别为、，方差分别为、，则
A．， B．， C．， D．，
10．若不等式的解集是，则下列各点可能在一次函数的图象上的是
A．（1，3） B．（5，1） C．（，） D．（2，）
二、填空题：本题共6小题，每小题4分，共24分。
11．当a________时，分式有意义．
12．计算：________．
13．如图，在菱形ABCD中，AC和BD是对角线，，则________度．
14．若a、b、c的平均数是5，d、e的平均数是10，则a、b、c、d、e的平均数是________．
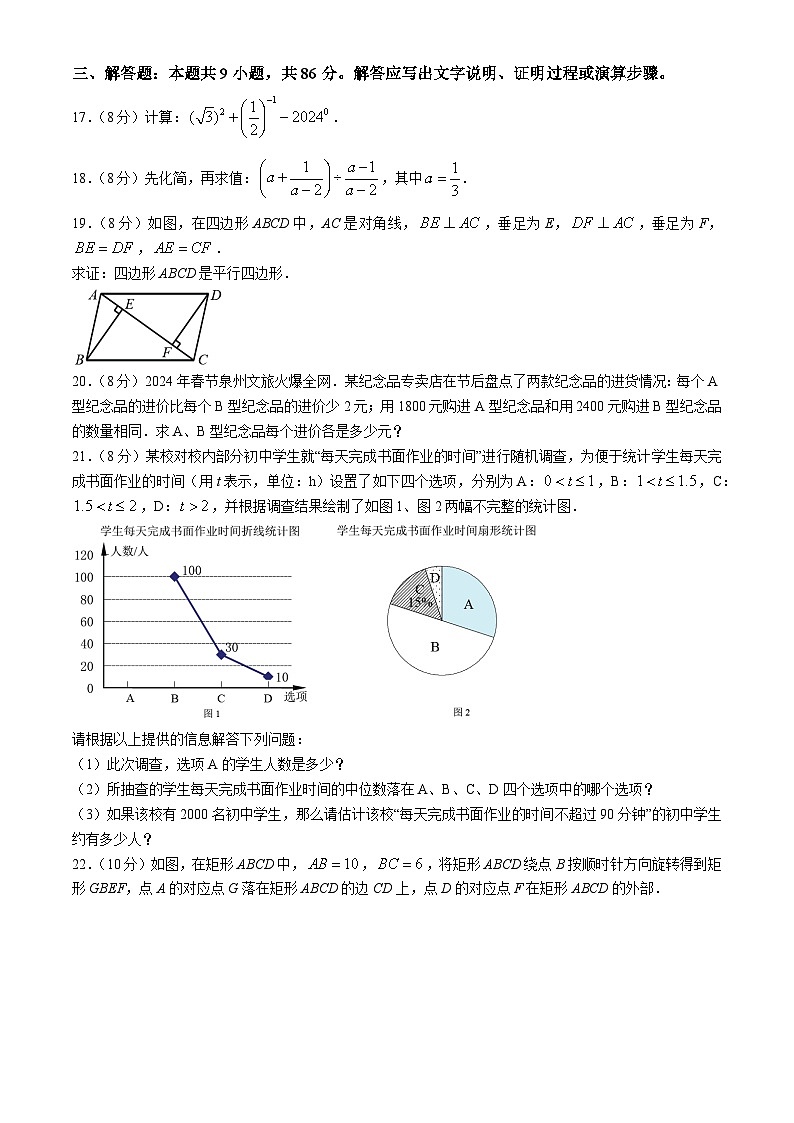
15．如图，已知一次函数的图象与反比例函数（）的图象相交于点A与点B，若点A的坐标为（1，3），则点B的坐标为________．
16．如图，在矩形ABCD中，点M在边CD上，将沿着直线BM折叠，点C的对称点N在边AD上，过点C作于点F，与BM相交于点E，延长CF交AB于点G，当G为边AB的中点时，有（m、n是有理数），则________．
三、解答题：本题共9小题，共86分。解答应写出文字说明、证明过程或演算步骤。
17．（8分）计算：．
18．（8分）先化简，再求值：，其中．
19．（8分）如图，在四边形ABCD中，AC是对角线，，垂足为E，，垂足为F，，．
求证：四边形ABCD是平行四边形．
20．（8分）2024年春节泉州文旅火爆全网．某纪念品专卖店在节后盘点了两款纪念品的进货情况：每个A型纪念品的进价比每个B型纪念品的进价少2元；用1800元购进A型纪念品和用2400元购进B型纪念品的数量相同．求A、B型纪念品每个进价各是多少元？
21．（8分）某校对校内部分初中学生就“每天完成书面作业的时间”进行随机调查，为便于统计学生每天完成书面作业的时间（用t表示，单位：h）设置了如下四个选项，分别为A：，B：，C：，D：，并根据调查结果绘制了如图1、图2两幅不完整的统计图．
请根据以上提供的信息解答下列问题：
（1）此次调查，选项A的学生人数是多少？
（2）所抽查的学生每天完成书面作业时间的中位数落在A、B、C、D四个选项中的哪个选项？
（3）如果该校有2000名初中学生，那么请估计该校“每天完成书面作业的时间不超过90分钟”的初中学生约有多少人？
22．（10分）如图，在矩形ABCD中，，，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点A的对应点G落在矩形ABCD的边CD上，点D的对应点F在矩形ABCD的外部．
（1）尺规作图：作矩形GBEF（保留作图痕迹，不写作法）；
（2）求点C到EF的距离．
23．（10分）【综合与实践】某兴趣小组利用物理学中杠杆原理制作简易跷跷板，小组先设计方案，然后动手制作，再结合实际进行调试．请完成下列方案设计中的任务．
【知识背景】如图，在木板的左端有一个固定质量为千克的靠背，质量为m千克的小孩紧贴靠背而坐，选定木板中点偏右的位置作为跷跷板的支点，支点与靠背的距离为l米，选定支点右侧a米处为零刻度线．质量为M千克的大人坐在零刻度线的右侧，大人可以通过调整自己的位置使跷跷板保持平衡．
设大人与零刻度线的距离为y米，根据杠杆原理可得：．
【方案设计】目标：设计有标注刻度的简易跷跷板，使得两边分别坐上人后跷跷板平衡．设定，，零刻度线与末刻度线的距离定为1米．
任务一：确定l和a的值．
（1）当跷跷板左边不坐上小孩，且大人在零刻度线时，跷跷板平衡，则l与a的关系式：________；
（2）当跷跷板左边坐上质量为20千克的小孩，大人从零刻度线移至末刻度线时，跷跷板平衡，则l与a的关系式：________；
（3）根据（1）和（2）的结论可得l与a的值：________，________；
任务二：确定刻度线的位置．
（4）根据任务一，求y关于m的函数表达式；
（5）从零刻度线开始，小孩这端的质量每增加5千克，大人坐在木板上移动一个刻度能使跷跷板保持平衡，求相邻刻度线间的距离．
24．（13分）在平面直角坐标系xOy中，函数的图象与函数（）的图象相交于点B（1，5），与x轴交于点A，点C在线段AB上．
（1）求k和b的值；
（2）如图，当时，将绕点O顺时针旋转，使点B的对应点落在x轴正半轴上，得到，判断点是否在函数（）的图象上，并说明理由；
（3）当时，对于x的每一个值，函数的值总小于函数的值，直接写出n的取值范围．
25．（13分）如图1，在正方形ABCD中，E是边BC上的一点，在AE的右上方作正方形AEFG，连接DG．
（1）求证：；
（2）如图2，连接BG、BD、BF、DF，记、的面积分别为、，求的值；
（3）如图3，当点E在边BC的延长线上时，连接AF，交线段DG于点M，当时，试判断CG与DM的数量关系，并加以证明．
晋江市2024年春初中学科抽测诊断初二数学
参考答案及评分标准
说明：
（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．
（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．
（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数．
一、选择题：（每小题4分，共40分）
1．C 2．B 3．A 4．A 5．B 6．B 7．D 8．C 9．D 10．A
二、填空题：（每小题4分，共24分）
11． 12．1 13．30 14．7 15．（3，1） 16．8
三、解答题：（共86分）
17．（8分）解：原式
．
（其它解法，请参照以上评分标准）
18．（8分）解：原式
．
当时，原式．
（其它解法，请参照以上评分标准）
19．（8分）证明：∵，，
∴．
在和中，
∴．
∴，，
∴，
∴四边形ABCD是平行四边形．
（其它解法，请参照以上评分标准）
20．（8分）解：设每个A型纪念品的进价为x元，则每个B型纪念品的进价为元．
依题意，得，
解得．
经检验，是原方程的解，且符合题意，则．
答：每个A型纪念品的进价为6元，每个B型纪念品的进价为8元．
（其它解法，请参照以上评分标准）
21．（8分）解：（1）此次调查的总人数是（人），
选项A的学生人数是（人）．
答：选项A的学生人数是60人．
（2）选项B．
（3）（人）．
答：估计该校“每天完成书面作业的时间不超过90分钟”的初中学生约有1600人．
（其它解法，请参照以上评分标准）
22．（10分）解：（1）如图1，矩形GBEF是所求作的矩形；
（2）如图2，由矩形的性质及旋转的性质可得
，．
过点C作，分别交EF和BG于点M、N．
∵四边形GBEF是矩形，
∴，．
∴四边形MNBE是平行四边形，
又∵，∴□MNBE是矩形．
∴，．
在中，由勾股定理，得．
∵，
∴，．
∴．
（其它解法，请参照以上评分标准）
23．（10分）解：（1）5a； （2）； （3），；
（4）由（3）可知，，
∴，∴．
（5）由（4）可知．
∴当时，；当时，；
∴相邻刻度线间的距离为0.25m．
（其它解法，请参照以上评分标准）
24．（13分）解：（1）∵函数的图象与函数（）的图象相交于点B（1，5），
∴，，∴，；
（2）点不在函数（）的图象上，理由如下：
如图，过点C作轴于点N，过点B作轴，交NC的延长线于点M．
由（1）得，∴一次函数的表达式为，令，则，∴A（，0）．
∵点C在线段AB上，∴设点C（t，）．
又∵点B（1，5），∴，，，．
∵，∴，
由勾股定理，得，，
∴，
∴，解得．
∴C（，）．
∵，，
∴．
由旋转的性质得，
∴，，
过作轴于P，则，
∴．
设（，），
∵，
∴，
∴点不在函数（）的图象上．
（3）．
（其它解法，请参照以上评分标准）
25．（13分）解：（1）如图1．
∵四边形ABCD和四边形AEFG都是正方形，
∴，，，
∴，，
∴．
在和中，
∴．
∴，
（2）如图2，由（1）得，∴，即，
∴C、D、G三点共线．
连接CF，过点F作，交BC的延长线于点H．
∴．
∵，，
∴．
∵四边形ABCD和四边形AEFG都是正方形，
∴，，，．
在和中，
∴．
∴，．
∵，
∴，即，
∴，
∴是等腰直角三角形，
∴，
∴．
∴．
∵，
∴，
∴，．
（3）．理由如下：
如图3，同（1）（2）可证得，C、D、G三点共线．
连接ME，设正方形ABCD的边长为a，，则，，，
∴，
∴，
由正方形的轴对称性，得，
在中，由勾股定理，得，
∴，整理得，又，解得．
∴，，
∴．
∴，即．
（其它解法，请参照以上评分标准）