


专题03 概率投影和视图(考点清单)-九年级上学期数学期末考点大串讲(北师大版)
展开【考点1】概率有关运算 【考点2】利用频率估计概率.菁
【考点3】平行投影. 【考点4】中心投影
【考点5】几何体的视图 【考点6】由三视图判断几何体
【考点7 】 作图-三视图
【考点1】概率有关运算
1.(2023秋•新民市期中)小华抛一枚质地均匀的硬币两次,分别是正、反面各一次朝上的概率是( )
A.B.C.D.
【答案】C
【解答】解:列表如下:
共有4种等可能的结果,其中分别是正、反面各一次朝上的结果有2种,
∴分别是正、反面各一次朝上的概率是.
故选:C.
2.(2023•林州市模拟)在如图所示的电路中,随机闭合开关S1、S2、S3中的两个,能让灯泡L1发光的概率是( )
A.B.C.D.
【答案】B
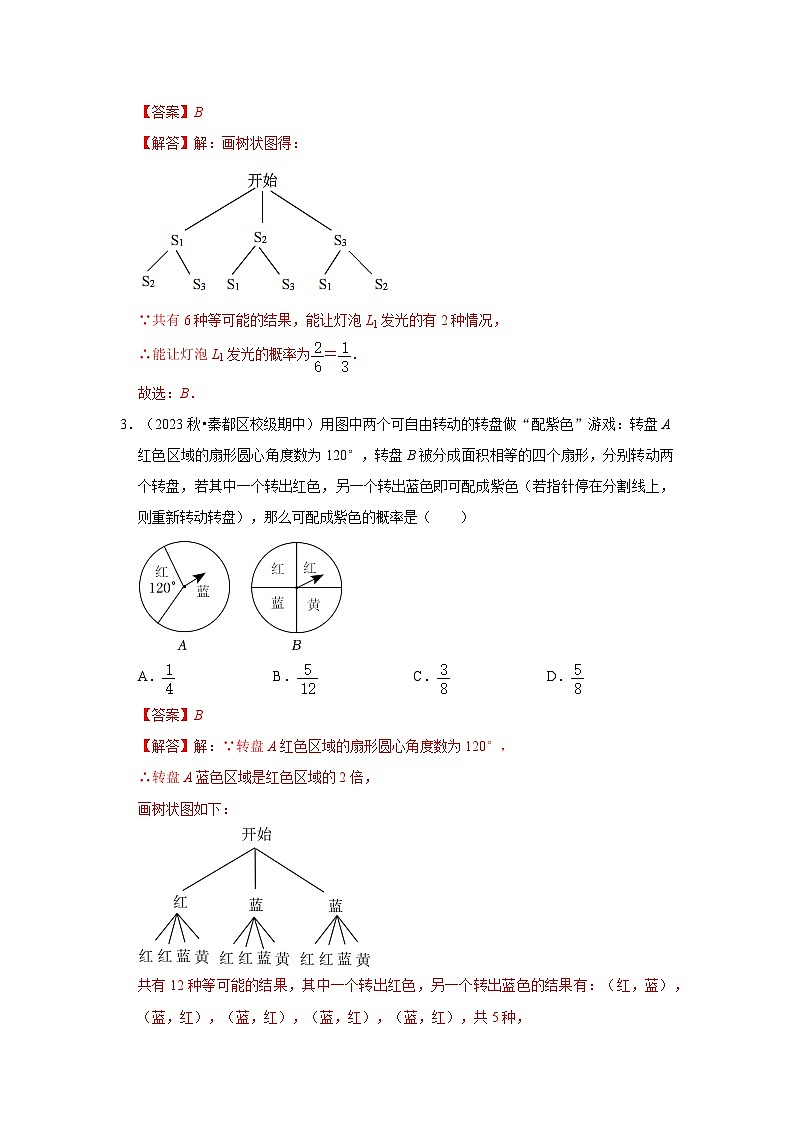
【解答】解:画树状图得:
∵共有6种等可能的结果,能让灯泡L1发光的有2种情况,
∴能让灯泡L1发光的概率为=.
故选:B.
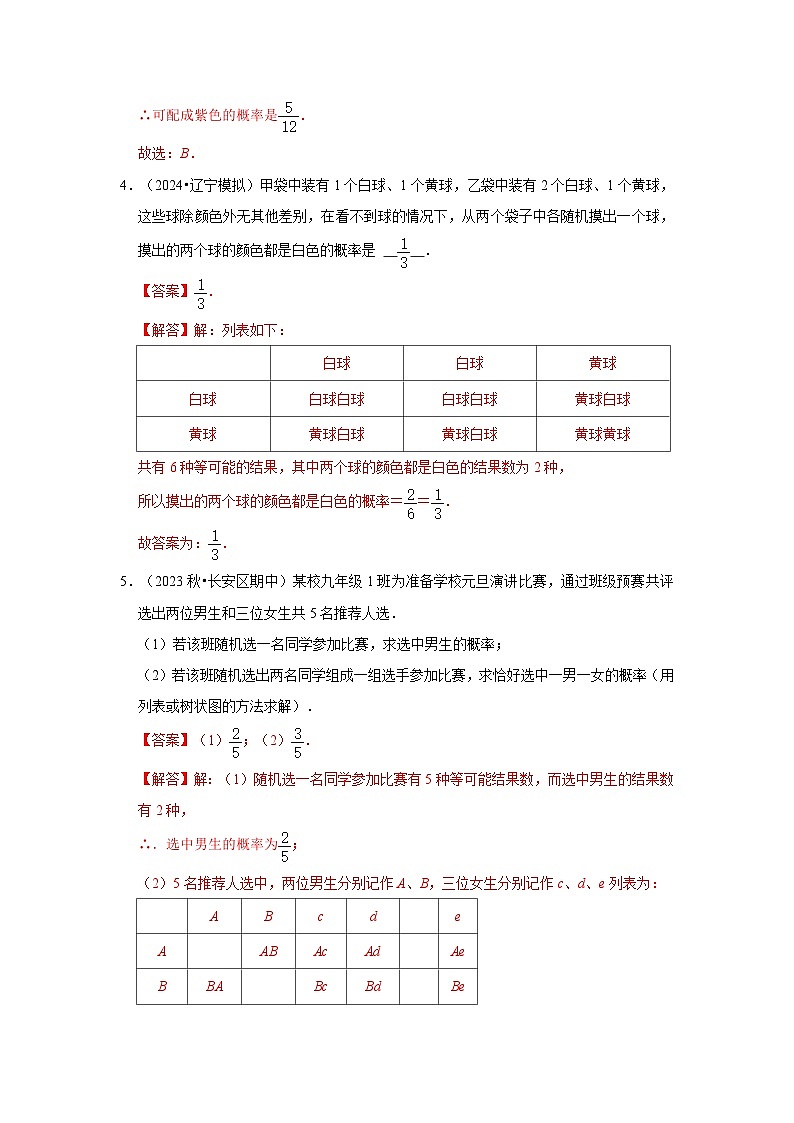
3.(2023秋•秦都区校级期中)用图中两个可自由转动的转盘做“配紫色”游戏:转盘A红色区域的扇形圆心角度数为120°,转盘B被分成面积相等的四个扇形,分别转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色(若指针停在分割线上,则重新转动转盘),那么可配成紫色的概率是( )
A.B.C.D.
【答案】B
【解答】解:∵转盘A红色区域的扇形圆心角度数为120°,
∴转盘A蓝色区域是红色区域的2倍,
画树状图如下:
共有12种等可能的结果,其中一个转出红色,另一个转出蓝色的结果有:(红,蓝),(蓝,红),(蓝,红),(蓝,红),(蓝,红),共5种,
∴可配成紫色的概率是.
故选:B.
4.(2024•辽宁模拟)甲袋中装有1个白球、1个黄球,乙袋中装有2个白球、1个黄球,这些球除颜色外无其他差别,在看不到球的情况下,从两个袋子中各随机摸出一个球,摸出的两个球的颜色都是白色的概率是 .
【答案】.
【解答】解:列表如下:
共有6种等可能的结果,其中两个球的颜色都是白色的结果数为2种,
所以摸出的两个球的颜色都是白色的概率==.
故答案为:.
5.(2023秋•长安区期中)某校九年级1班为准备学校元旦演讲比赛,通过班级预赛共评选出两位男生和三位女生共5名推荐人选.
(1)若该班随机选一名同学参加比赛,求选中男生的概率;
(2)若该班随机选出两名同学组成一组选手参加比赛,求恰好选中一男一女的概率(用列表或树状图的方法求解).
【答案】(1);(2).
【解答】解:(1)随机选一名同学参加比赛有5种等可能结果数,而选中男生的结果数有2种,
∴.选中男生的概率为;
(2)5名推荐人选中,两位男生分别记作A、B,三位女生分别记作c、d、e列表为:
共有20种等可能的结果数,其中恰好选中一男一女的结果数为12种.
所以恰好选中一男一女的概率为=.
6.(2023•随州)中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式,根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
(1)接受问卷调查的学生共有 80 人,条形统计图中m的值为 16 ,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为 90° ;
(2)若该校共有学生800人,根据上述调查结果,可以估计出该校学生中对心理健康知识“不了解”的总人数为 40 人;
(3)若某班要从对心理健康知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加心理健康知识竞赛,请用列表或画树状图的方法,求恰好抽到2名女生的概率.
【答案】(1)80,16,90°;
(2)40;
(3).
【解答】解:(1)∵基本了解的有40人,占50%,
∴接受问卷调查的学生共有40÷50%=80(人),
条形统计图中m的值为:80﹣20﹣40﹣4=16,
扇形统计图中“非常了解”部分所对应扇形的圆心角的度数为:=90°,
故答案为:80,16,90°;
(2)可以估计出该校学生中对心理健康知识“不了解”的总人数为:800×=40人),
故答案为:40;
(3)画树状图如下:
一共有12种等可能的结果,其中恰好抽到2名女生的结果有2种,
∴P(恰好抽到2名女生)=.
【考点2】利用频率估计概率
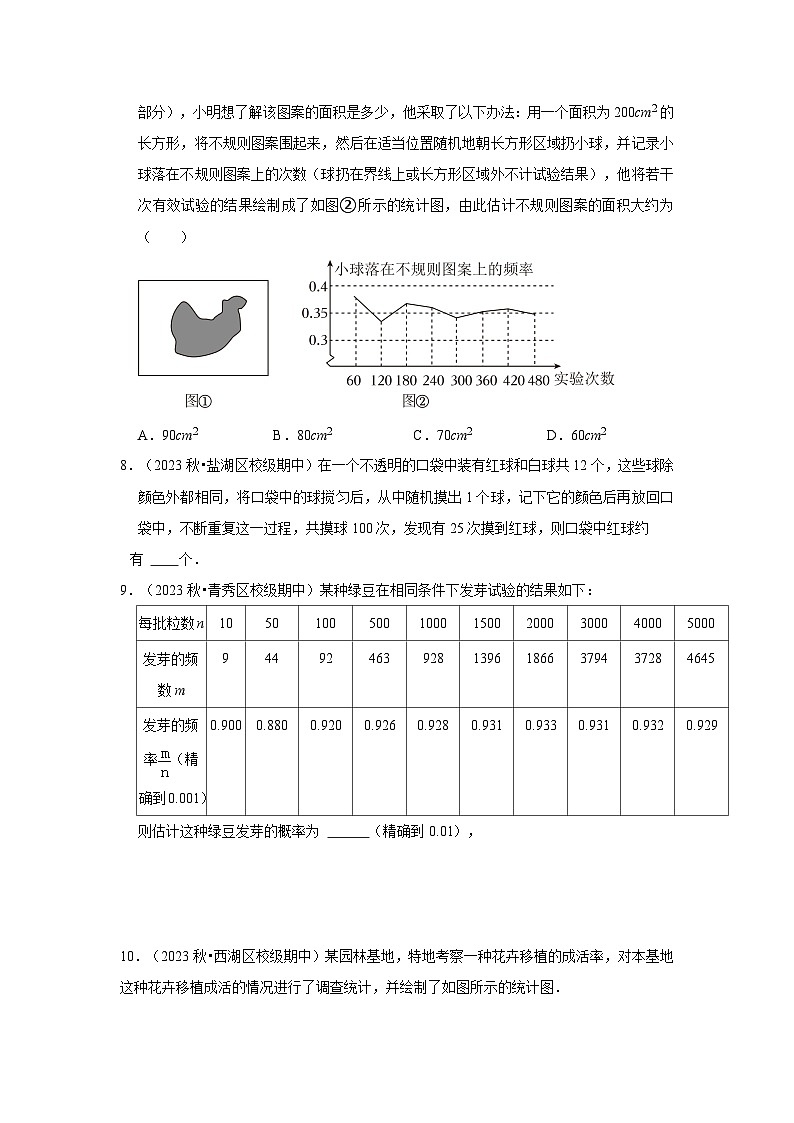
7.(2023秋•锦江区校级期中)如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个面积为200cm2的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了如图②所示的统计图,由此估计不规则图案的面积大约为( )
A.90cm2B.80cm2C.70cm2D.60cm2
【答案】C
【解答】解:假设不规则图案面积为x cm2,
由已知得:长方形面积为200cm2,
根据几何概率公式小球落在不规则图案的概率为:,
当事件A试验次数足够多,即样本足够大时,其频率可作为事件A发生的概率估计值,
故由折线图可知,小球落在不规则图案的概率大约为0.35,
综上有:=0.35,
解得:x=70,
所以估计不规则图案的面积大约为70cm2.
故选:C.
8.(2023秋•盐湖区校级期中)在一个不透明的口袋中装有红球和白球共12个,这些球除颜色外都相同,将口袋中的球搅匀后,从中随机摸出1个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸球100次,发现有25次摸到红球,则口袋中红球约有 3 个.
【答案】3.
【解答】解:设红球有x个,
则,
解得x=3,
∴红球的个数约为3个.
故答案为:3.
9.(2023秋•青秀区校级期中)某种绿豆在相同条件下发芽试验的结果如下:
则估计这种绿豆发芽的概率为 0.93 (精确到0.01),
【答案】0.93.
【解答】解:由表中的发芽的频率可知,
当实验次数的增多,发芽的频率越来越稳定在0.93左右,所以可估计这种绿豆发芽的机会大约是0.93.
故答案为:0.93.
10.(2023秋•西湖区校级期中)某园林基地,特地考察一种花卉移植的成活率,对本基地这种花卉移植成活的情况进行了调查统计,并绘制了如图所示的统计图.
请你根据统计图提供的信息,回答下列问题:
(1)这种花卉成活的频率稳定在 0.9 附近,估计成活概率为 0.9 .(精确到0.1)
(2)该园林基地已经移植这种花卉10000棵.
①估计这批花卉成活的棵数;
②根据某大型小区需要成活99000棵这种花卉,估计还需要移植多少棵?
【答案】(1)0.9,0.9;
(2)①9000棵;②100000棵.
【解答】解:(1)由图可知,这种花卉成活的频率稳定在0.9附近,估计成活概率为0.9;
故答案为:0.9,0.9;
(2)①10000×0.9=9000(棵),
答:估计这种花卉成活9000棵;
②99000÷0.9﹣10000=100000(棵),
答:估计还要移植100000棵.
【考点3】平行投影.
11.(2023秋•福山区期中)平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B. C. D.
【答案】D
【解答】解:根据平行投影的定义可知,在某一时刻三根木杆在阳光下的影子可能是:
故选:D.
12.(2023秋•宝安区期中)下列四幅图形中,表示两棵圣诞树在同一时刻阳光下的影子的图形可能是( )
A. B. C. D.
【答案】B
【解答】解:A、影子的方向不相同,错误;
B、影子平行,且较高的树的影子长度大于较低的树的影子,正确;
C、相同树高与影子是成正比的,较高的树的影子长度小于较低的树的影子,错误;
D、影子的方向不相同,错误;
故选:B.
13.(2022秋•文登区期末)若只增大物体与投影面之间的距离,则其正投影( )
A.变大B.变小C.不变D.无法确定
【答案】C
【解答】解:若只增大物体与投影面之间的距离,则其正投影不变.
故选:C.
14.(2022秋•细河区期末)如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
A.1.5mB.1.6mC.1.86mD.2.16m
【答案】A
【解答】解:∵BE∥AD,
∴△BCE∽△ACD,
∴即=
且BC=1,DE=1.8,EC=1.2
∴=
∴1.2AB=1.8,
∴AB=1.5m.
故选:A.
15.(2023秋•霞浦县期中)数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
请你根据以下两种方案,选择其中一种方案,求出旗杆的高度.
方案一:如图1,小明在地面直立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶点E、旗杆的顶点A在同一直线上.测量:人与标杆的距离DF=1m,人与旗杆的距离DB=16m,人的目高和标杆的高度差EG=0.9m,人的目高CD=1.6m.
方案二:如图2,小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21米,留在墙上的影高CD=2米.
【答案】见解析,旗杆的高度是16米.
【解答】解:方案一:如图1所示:
由已知得:CD∥EF∥AB,
∴△ECG∽△ACH,
∴=,即=,
解得:AH=14.4米,
∴AB=AH+BH=14.4+1.6=16(米);
答:旗杆的高度是16米;
方案二:如图所示,延长AC,BD相交于点E,
则CD:DE=1:1.5,得DE=1.5CD=3米,
由已知CD∥AB,
∴△ABE∽△CDE,
∴=,即=,
解得:AB=16.
答:旗杆的高度是16米.
【考点4】中心投影
16.(2023秋•高新区校级期中)下列哪种影子不是中心投影( )
A.月光下房屋的影子 B.晚上在房间内墙上的手影
C.都市冤虹灯形成的影子 D.皮影戏中的影子
【答案】A
【解答】解:晚上在房间内墙上的手影,都市冤虹灯形成的影子,皮影戏中的影子,是中心投影,
月光下下房屋的影子是平行投影,不是中心投影.
故选:A.
17.(2023•松阳县二模)如图,树AB在路灯O的照射下形成投影AC,若树高AB=2m,树影AC=3m,树与路灯的水平距离AP=4.5m,则路灯的高度OP是( )
A.3B.4C.5D.6
【答案】C
【解答】解:∵AB∥OP,
∴△ACB∽△PCO,
∴=,
∴=,
∴OP=5(m),
故选:C.
18.(2023秋•桂平市期中)如图,路灯距地面8米,身高1.6米的小明从点A处沿AO所在的直线行走14m到点B时,人影长度( )
A.变长3.5mB.变长2.5mC.变短3.5mD.变短2.5m
【答案】C
【解答】解:设小明在A处时影长为x,AO长为a,B处时影长为y.
∵AC∥OP,BD∥OP,
∴△ACM∽△OPM,△BDN∽△OPN,
∴,,
则,
∴x=;
,
∴y=,
∴x﹣y=3.5,
故变短了3.5米.
故选:C.
20.(2022秋•临淄区期末)在乡村振兴中,农村也装上了路灯,照亮了农民夜晚回家的路.某天夜晚,一棵树和王大伯在路灯照射下的影子如图所示,则路灯的位置为( )
A.a处B.b处C.c处D.d处
【答案】B
【解答】解:如图,观察图象可知,路灯的位置在b处.
故选:B.
21.(2022秋•市北区校级期末)如果在同一时刻的阳光下,小莉的影子比小玉的影子长,那么在同一路灯下( )
A.小莉的影子比小玉的影子长 B.小莉的影子比小玉的影子短
C.小莉的影子和小玉的影子一样长 D.无法判断谁的影子长
【答案】D
【解答】解:路灯是点光源,高度较低,在同一路灯下,身高影响身体影长,人站的位置更会影响身体影长.因此,小莉和小玉的影子长短,由于站立位置不同,无法确定谁的更长,故D正确,其他选项错误.
故选:D
【考点5】几何体的视图
22.(2023秋•锦江区校级期中)如图所示的几何体的主视图是( )
A.B.C.D.
【答案】A
【解答】解:从正面看,可得如下图形:
.
故选:A.
23.(2023秋•碑林区校级期中)如图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是( )
A.B. C.D.
【答案】A
【解答】解:根据左视图的定义,从左边观察得到的图形,是选项A.
故选:A.
24.(2023秋•灞桥区校级期中)如图所示,该几何体的左视图为( )
A. B. C. D.
【答案】A
【解答】解:从几何体的左面看,是一个矩形,因为中间的棱可看见,所以矩形的中间有一条横向的实线.
故选:A.
25.(2023•鄱阳县一模)如图是一个空心圆柱体,其主视图是( )
A.B.C.D.
【答案】D
【解答】解:从前面观察物体可以发现:它的主视图应为矩形,
又因为该几何体为空心圆柱体,故中间的两条棱在主视图中应为虚线,
故选:D.
26.(2023春•文山州期末)如图是用六块大小相同的小正方体搭建的一个立体几何体,从正面看到的形状是( )
A. B. C. D.
【答案】C
【解答】解:从正面看,底层是三个小正方形,上层的右边是一个小正方形,
故选:C.
【考点6】由三视图判断几何体
27.(2023秋•城关区校级期中)一个立体图形,从正面看到的形状是,从左面看到的形状是.它可能是下面的哪一个( )
A.B.
C.D.
【答案】A
【解答】解:从左面看到的是三个正方形,右边一列二个正方形,左边一个正方形与右边一列下边的一个成一行;由此可得这个立体图形可能是.
故选:A.
28.(2023秋•文登区期中)如图为一个几何体的三视图,那么这个几何体是( )
A.圆锥B.圆柱C.三棱柱D.三棱锥
【答案】A
【解答】解:由于俯视图为圆形可得为球、圆柱、圆锥.主视图和左视图为三角形可得此几何体为圆锥.
故选:A.
29.(2023•顺义区一模)如图是某个几何体的三视图,则该几何体是( )
A.圆锥B.长方体C.三棱柱D.圆柱
【答案】D
【解答】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是圆可判断出这个几何体是圆柱.
故选:D.
30.(2023秋•济南期中)一个几何体的主视图和俯视图如图所示,若这个几何体最多由a个小正方体组成,最少由b个小正方体组成,则a+b等于( )
A.10B.11C.12
【答案】C
【解答】解:结合主视图和俯视图可知,左边后排最多有3个,左边前排最多有3个,右边只有一层,且只有1个,
所以图中的小正方体最多7块,
结合主视图和俯视图可知,左边后排最少有1个,左边前排最多有3个,右边只有一层,且只有1个,
所以图中的小正方体最少5块,
a+b=12,
故选:C
【考点7 】 作图-三视图
31.(2023秋•英德市期中)如图是由6个大小相同的小立方体块搭建的几何体.
(1)请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图;
(2)在不改变从左面、上面看到的形状图的前提下,最多可以添加 4 个大小相同的小立方体块.
【答案】(1)见解析;
(2)4.
【解答】解:(1)该几何体从三个不同方向看到的形状图如下:
(2)在从正面看得到的图形中,在下面四个位置放上小小立方体块,不改变从左面、上面看到的形状图,
故答案为:4.
32.(2023秋•金牛区校级期中)如图是用棱长为1cm的小正方体组成的简单几何体.
(1)在网格中画出这个几何体从三个方向看到的形状图;
(2)这个几何体的体积是 6 cm3.
【答案】(1)见解答.
(2)6.
【解答】解:(1)如图所示.
(2)这个几何体的体积是13×6=6(cm3).
故答案为:6.
33.(2023秋•锦江区校级期中)如图是由棱长都为2cm的小正方体组成的简单几何体.
(1)请在方格内分别画出从这个几何体的三个不同方向看到的形状图;
(2)求出该几何体的体积和表面积.
【答案】(1)见解答.
(2)该几何体的体积为48cm3,表面积为104cm2.
【解答】解:(1)如图所示.
(2)体积为23×6=48(cm3).
表面积为(5+4+4)×2×22=104(cm2).
答:该几何体的体积为48cm3,表面积为104cm2.
正
反
正
(正,正)
(正,反)
反
(反,正)
(反,反)
白球
白球
黄球
白球
白球白球
白球白球
黄球白球
黄球
黄球白球
黄球白球
黄球黄球
A
B
c
d
e
A
AB
Ac
Ad
Ae
B
BA
Bc
Bd
Be
c
cA
cB
cd
ce
d
dA
dB
dc
de
e
eA
eB
ec
ed
每批粒数n
10
50
100
500
1000
1500
2000
3000
4000
5000
发芽的频数m
9
44
92
463
928
1396
1866
3794
3728
4645
发芽的频率(精确到0.001)
0.900
0.880
0.920
0.926
0.928
0.931
0.933
0.931
0.932
0.929
专题03 位置与坐标(考点清单) -八年级上学期数学期末考点大串讲(北师大版): 这是一份专题03 位置与坐标(考点清单) -八年级上学期数学期末考点大串讲(北师大版),文件包含专题03位置与坐标考点清单原卷版docx、专题03位置与坐标考点清单解析版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版): 这是一份专题08 圆(考点清单,12个考点)-九年级上学期数学期末考点大串讲(北师大版),文件包含专题08圆考点清单12个考点原卷版docx、专题08圆考点清单12个考点解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
猜题03 概率、投影和视图(易错必刷30题7种题型专项训练)-九年级上学期数学期末考点大串讲(北师大版): 这是一份猜题03 概率、投影和视图(易错必刷30题7种题型专项训练)-九年级上学期数学期末考点大串讲(北师大版),文件包含猜题03概率投影和视图易错必刷30题7种题型专项训练原卷版docx、猜题03概率投影和视图易错必刷30题7种题型专项训练解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。












