
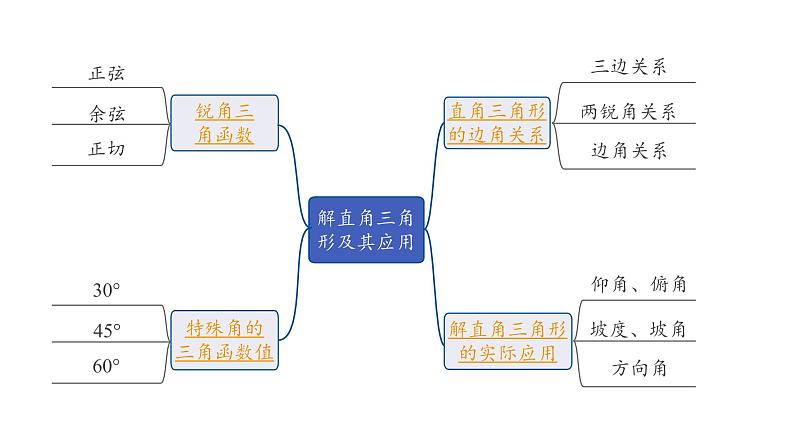




2024内蒙古中考数学一轮知识点复习 第23课时 解直角三角形及其应用(课件)
展开【对接教材】北师:九下第一章P1~P27; 人教:九下第二十八章P60~P85.
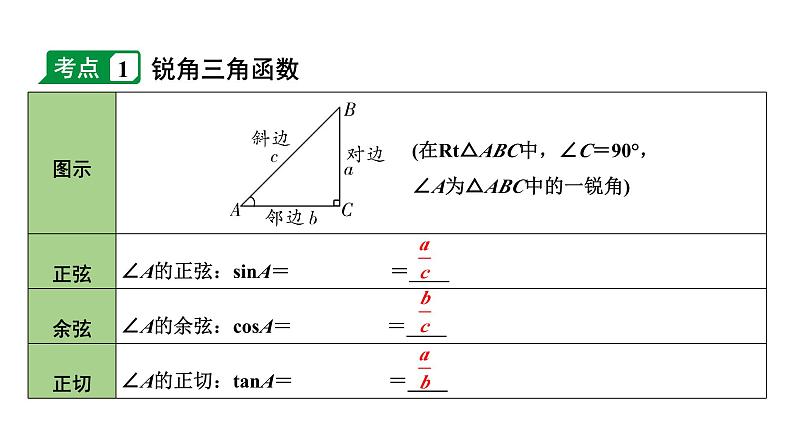
(在Rt△ABC中,∠C=90°,∠A为△ABC中的一锐角)
1. 在Rt△ABC中,∠C=90°,AB=4,BC=3,则csB的值为( ) A. B. C. D.
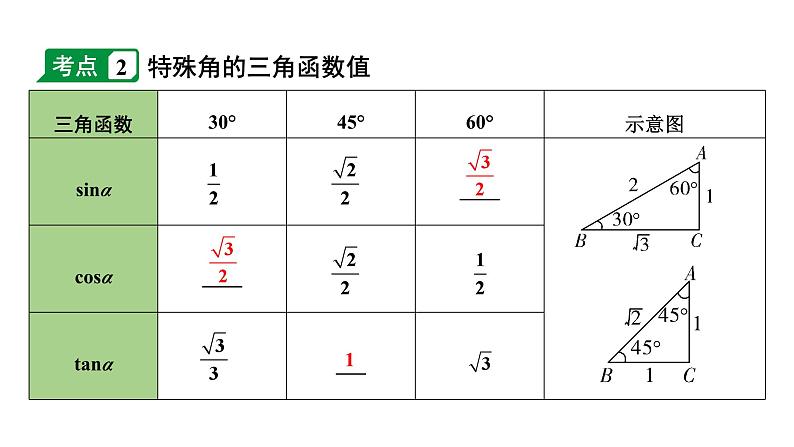
2. 在△ABC中,∠A,∠B满足|csA- |+(1-tanB)2=0,则∠C的大小是( ) A.45° B. 60° C. 75° D. 105°
3. 在Rt△ABC中,AC=5,∠C=90°,csB= ,则AB=____,BC=___,sinA=____.
解直角三角形的实际应用
4. 已知,一艘货船在A处,巡逻艇C在其南偏西60°的方向上.(1)如图①,A处在巡逻艇C的___________方向上;(2)如图②,一艘客船在B处,巡逻艇C在其南偏西30°的方向上.①此时从巡逻艇上看这两艘船的视角∠ACB的度数为_____;②若BC=4海里,则货船沿AC方向航行过程中距离客船B的最短距离为___海里.
解直角三角形的实际应用 (包头2考,呼和浩特5考,赤峰4考)
1. (2023赤峰17题3分)如图,一根竖直的木杆在离地面3.1 m处折断,木
杆顶端落在地面上,且与地面成38°角,则木杆折断之前的高度约为____ m.(参考数据:sin38°≈0.62,cs38°≈0.79,tan38°≈0.78)
二、解两个直角三角形 类型一 母子型
2. (2021呼和浩特20题8分)如图,线段EF与MN表示某一段河的两岸,EF∥MN.综合实践课上,同学们需要在河岸MN上测量这段河的宽度(EF与MN之间的距离),已知河对岸EF上有建筑物C、D,且CD=60米,同学们首先在河岸MN上选取点A处,用测角仪测得C建筑物位于A北偏
东45°方向,再沿河岸走20米到达B处,测得D建筑物位于B北偏东55°方向,请你根据所测数据求出该段河的宽度.(用非特殊角的三角函数或根式表示即可)
解:如解图,分别过点C、D作CP⊥MN,DQ⊥MN,垂足为P、Q,
3. (2021赤峰16题3分)某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C观测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头C处的高度CD为238米,点A,D,B在同一直线上,则雪道AB的长度为_____米.(结果保留整数,参考数据:sin50°≈0.77,cs50°≈0.64,tan50°≈1.19)
4. (2023呼和浩特20题7分)如图①,已知甲地在乙地的正东方向,因有大山阻隔,由甲地到乙地需要绕行丙地,已知丙地位于甲地北偏西30°方向,距离甲地460 km,丙地位于乙地北偏东66°方向,现要打通穿山隧道,建成甲乙两地直达高速公路,如果将甲、乙、丙三地当作三个点A、
B、C,可抽象成如图②所示的三角形,求甲乙两地之间直达高速线路的长AB.(结果用含非特殊角的三角函数和根式表示即可)
解:如解图,过点C作CD⊥AB于点D,
5. (2021包头22题8分)某工程队准备从A到B修建一条隧道,测量员在直线AB的同一侧选定C,D两个观测点,如图,测得AC长为 km,CD长为 ( + )km,BD长为 km,∠ACD=60°,∠CDB=135°(A、B、C、D在同一水平面内).(1)求A、D两点之间的距离;
解:(1)如解图,过点A作AE⊥CD,垂足为E,
∴AE= ·sin60°= .∵cs∠ACE= ,∴CE= ·cs60°= .∵CD= ( ),∴DE=CD-CE= ,∵在Rt△AED中,AD= ,∴AD= ,∴A、D两点之间的距离为 km;
(2)求隧道AB的长度.
6. (2022包头22题8分)如图,一个人骑自行车由A地到C地途经B地,当他由A地出发时,发现他的北偏东45°方向有一电视塔P,他由A地向正北方向骑行了3 km到达B地,发现电视塔P在他北偏东75°方向,然后他由B地向北偏东15°方向骑行了6 km到达C地.(1)求A地与电视塔P的距离;
解:(1)由题意知∠A=45°,∠NBC=15°,∠NBP=75°,如解图,过点B作BE⊥AP于点E,则∠ABE=90°-45°=45°,
∴AE=BE.∵AB=3 ,∴AE=BE=3.在Rt△BEP中,∠EBP=180°-∠ABE-∠NBP=180°-45°-75°=60°,∴PE=BE·tan60°=3 ,∴AP=AE+PE=3+3 .答:A地与电视塔P的距离为(3+3 ) km;
(2)求C地与电视塔P的距离.
7. (2021甘肃省卷)如图①是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:方案设计:如图②,宝塔CD垂直于地面,在地面上选取A,B两处分别测得∠CAD和∠CBD的度数(A,D,B在同一条直线上).
数据收集:通过实地测量:地面上A,B两点的距离为58 m,∠CAD=42°,∠CBD=58°.问题解决:求宝塔CD的高度(结果保留一位小数).参考数据:sin42°≈0.67,cs42°≈0.74,tan42°≈0.90,sin58°≈0.85,cs58°≈0.53,tan58°≈1.60.根据上述方案及数据,请你完成求解过程.
2024内蒙古中考数学一轮知识点复习 第27课时 正方形(课件): 这是一份2024内蒙古中考数学一轮知识点复习 第27课时 正方形(课件),共36页。PPT课件主要包含了正方形,考点精讲,互相垂直平分且相等,直角或90°,互相垂直,中点四边形,BD交于点O,①②④等内容,欢迎下载使用。
2024内蒙古中考数学一轮知识点复习 第25课时 矩形(课件): 这是一份2024内蒙古中考数学一轮知识点复习 第25课时 矩形(课件),共21页。PPT课件主要包含了矩形的性质与判定,相等且互相平分,直角或90°,回归教材,例1题图,例2题图①,面积相等的等腰三角形,例2题图②,例3题图,例3题图③等内容,欢迎下载使用。
2024内蒙古中考数学一轮知识点复习 第8课时 分式方程及其应用(课件): 这是一份2024内蒙古中考数学一轮知识点复习 第8课时 分式方程及其应用(课件),共32页。PPT课件主要包含了分式方程及其应用,考点精讲,解分式方程,未知数,最简公分母,分式方程的实际应用,6-2x,-2x,-4x,x+8等内容,欢迎下载使用。












