

苏科版八年级数学上册同步考点必刷练精编讲义必刷基础练【2.2轴对称的性质】(原卷版+解析)
展开2.2 轴对称的性质
必刷知识点
知识点01:轴对称的性质
轴对称的性质:成轴对称的两个图形中,对应点的连被对称轴 ;成轴对称的两个图形的任何对应部分也成轴对称;成 的两个图形
知识点02:线段的垂直平分线
定义:
垂直并且平分一条线段的直线,叫做这条线段的 ,也叫线段的 .
知识点01:轴对称的性质
1.(2021八上·宜兴期中)下列结论中不正确的是( )
A.两个关于某直线对称的图形一定全等
B.对称图形的对称点一定在对称轴的两侧
C.两个成轴对称的图形对应点的连线的垂直平分线是它们的对称轴
D.有斜边和一锐角相等的两个直角三角形全等
2.(2021八上·沭阳月考)如图,六边形ABCDEF是轴对称图形, CF 所在的直线是它的对称轴,若∠AFC + ∠BCF = 150°,则∠AFE + ∠BCD 的大小是( )
A.150°B.300°C.210°D.330°
3.(2021八上·姜堰月考)如图, 内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则 的周长为( )
A.5cmB.10cmC.20cmD.15cm
4.(2021八上·江阴月考)下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等
B.轴对称图形至少有一条对称轴
C.全等的两个三角形一定能关于某条直线对称
D.等腰三角形是轴对称图形
5.(2021八上·陆川期中)下列说法:①全等的两个三角形一定成轴对称;②等腰三角形最少有1条对称轴,最多有3条对称轴;③成轴对称的两个图形一定全等;④任意两条相交直线都组成一个轴对称图形.其中正确的有 .(填序号)
6.(2021八上·沭阳月考)如图, 和 关于直线 对称,若 ,则图中阴影部分的面积为 .
7.(2021八上·江阴月考)黑板上写着 在正对着黑板的镜子里的像是 .
8.(2020八上·兴化月考)如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为
9.(2018八上·江都月考)如图:有一张直角三角形纸片ABC,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A’处,求∠A’DB的度数。
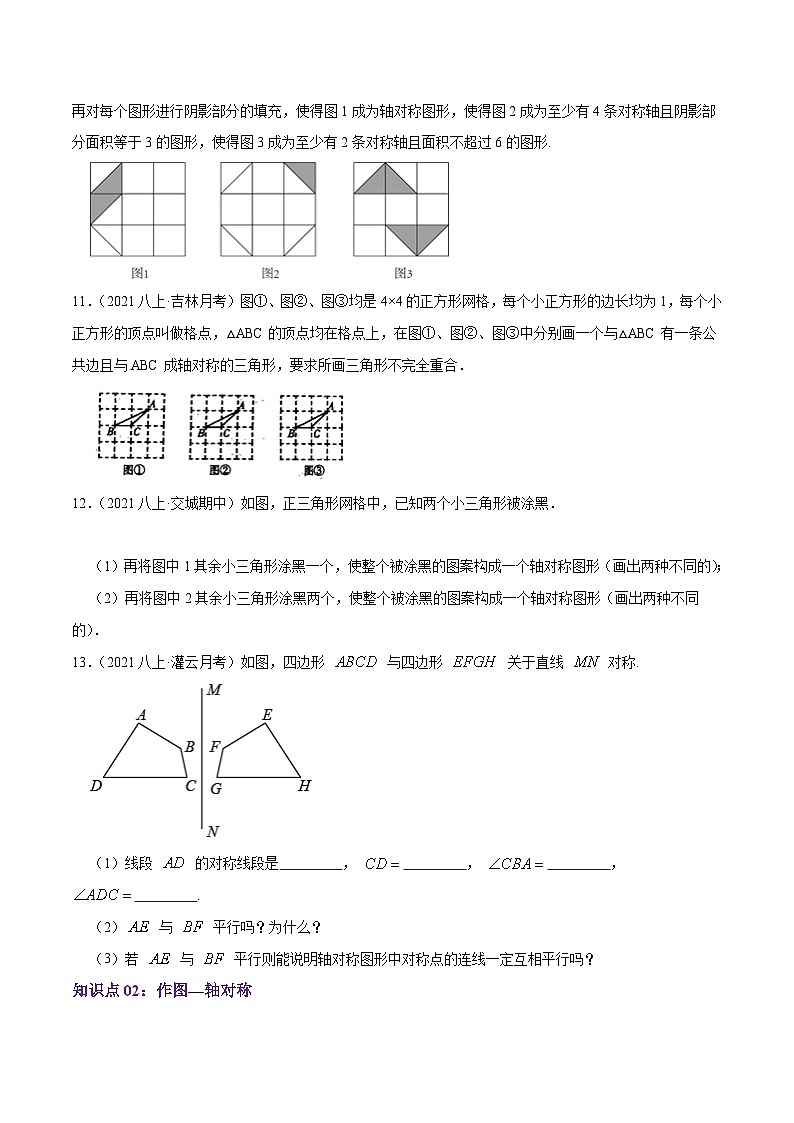
10.(2019八上·西城期中)下列各图中的单位小正方形的边长都等于1,并且都已经填充了一部分阴影,请再对每个图形进行阴影部分的填充,使得图1成为轴对称图形,使得图2成为至少有4条对称轴且阴影部分面积等于3的图形,使得图3成为至少有2条对称轴且面积不超过6的图形.
11.(2021八上·吉林月考)图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点均在格点上,在图①、图②、图③中分别画一个与△ABC有一条公共边且与ABC成轴对称的三角形,要求所画三角形不完全重合.
12.(2021八上·交城期中)如图,正三角形网格中,已知两个小三角形被涂黑.
(1)再将图中1其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的);
(2)再将图中2其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
13.(2021八上·灌云月考)如图,四边形 与四边形 关于直线 对称.
(1)线段 的对称线段是 , , , .
(2) 与 平行吗?为什么?
(3)若 与 平行则能说明轴对称图形中对称点的连线一定互相平行吗?
知识点02:作图—轴对称
14.(2018八上·蔡甸期中)如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个B.5个C.4个D.3个
15.(2018八上·田家庵期中)如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个.
A.3个B.4个C.5个D.6个
16.(2021八上·沂水期中)如图,在平面直角坐标系 中, 可以看作是 经过若干次的图形变化(轴对称、平移)得到的,写出一种由 得到 的过程: .
17.(2020八上·兴化月考)如图,在4×4的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有 个.
18.(2019八上·丰南期中)如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字 的格子内.
19.如图,在平面直角坐标系中,A(0,1),B(3, ),P为x轴上一动点,则PA+PB最小时点P的坐标为 .
20.(2021八上·惠州期末)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
⑴在图中作出关于y轴对称的;
⑵写出点的坐标(直接写答案);
⑶在y轴上画出点P,使PB+PC最小.
21.(2021八上·大埔期末)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
( 1 )请在如图所示的网格平面内作出平面直角坐标系;
( 2 )请作出△ABC关于y轴对称的△A′B′C′;
( 3 )写出点B′的坐标.
22.(2021八上·凤县期末)如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5),请回答下列问题:
(1)画出△ABC关于x轴的对称图形ΔA1B1C1;直接写出A1、B1、C1的坐标;
(2)如图,在直线 上找一点M,使得AM+BM的值最小.(保留作图痕迹)
知识点03:剪纸问题
23.(2021八上·长兴月考)如图,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是图中的哪一个( )
A.B.
C.D.
24.(2021八上·广州期末)如图,把一张长方形的纸,按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC是( )
A.直角三角形B.等边三角形
C.等腰三角形D.等腰直角三角形
25.(2020八上·洪泽月考)将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的爱心,将留下的纸片展开,得到的图形是( )
A. B.
C.D.
26.如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有 个不同的四边形.
27.(2021八上·鼓楼月考)剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A.B.C.D.
28.(2019八上·松山月考)如图,把一个正方形三次对折后沿虚线剪下,得到的图形是( )
A.B.C.D.
29.(2019八上·扬州月考)如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形如“ ”的图形,将纸片展开,得到的图形是( )
A.B.C.D.
30.(2018八上·丹徒月考)将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图形,再将图形的纸片展开铺平,得到的图案是( )
A.B.C.D.
31.如图所示,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点,把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是( )
A.正三角形B.正方形C.正五边形D.正六边形
32.(2017八上·东台月考)如图,将一正方形纸片沿图(1)、( 2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )
A.B.C.D.
知识点04:翻折变换(折叠问题)
33.(2021八上·驻马店期末)如图,有一条直的宽纸带,按图折叠,则∠α的度数等于( )
A.50°B.65°C.75°D.80°
34.(2021八上·川汇期末)如图,将的BC边对折,使点B与点C重合,DE为折痕,若,,则( ).
A.45°B.60°C.35°D.40°
35.(2021八上·西湖期中)如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA'再一次对折,点C落在BE上的C′处,此时∠C'BD=27°,则原三角形的∠C的度数为( )
A.27°B.59°C.79°D.69°
36.(2021八上·沙坪坝期末)如图所示,在 中, ,将 沿边 翻折得到 .若 ,则 的度数为( )
A.50°B.60°C.65°D.70°
37.(2020八上·无锡月考)经过以下变化后所得到的三角形不能和 全等的是( )
A.B.
C.D.
38.(2021八上·沭阳月考)如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′的位置处,若∠1=58°,则∠EFB的度数是 .
39.(2020八上·通山月考)如图,在三角形纸片中, ,沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,则 的周长等于 .
40.(2019八上·恩施期中)如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF= 度.
41.(2021八上·句容期末)如图,在三角形纸片 中, ,折叠该纸片,使点C落在 边上的D点处,折痕 与 交于点E,则折痕 的长为 .
42.(2021八上·毕节期末)如图,在平面直角坐标系中,长方形AOBC的边OB、OA分别在x轴、y轴上,点D在边BC上,将该长方形沿AD折叠,点C恰好落在边OB上的E处.若点 ,点 ,则点D的坐标是 .
43.(2022八上·博白期末)如图,将纸片沿折叠,使点落在点处,且平分,平分,若,则的度数为 .
44.(2021八上·丹东期末)如图,,点和点分别在边和边上,连接,将沿折叠,点的对应点是,若,则 .
45.(2021八上·浙江月考)如图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求AC和DC的长.
46.(2021八上·三水期中)如图,折叠矩形的一边 ,使点 落在 边的点 处,已知AB=8cm,BC=10cm,求 的长
47.(2021八上·温州期中)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处.求∠1+∠2的度数.
48.(2021八上·牡丹月考)十一国庆节,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.武玥同学在制作手工作品的第一、二个步骤是:
①先裁下了一张长 ,宽 的长方形纸片 ;
②如图,将纸片沿着直线 折叠,点 恰好落在 边上的 处.
请你根据①②步骤计算 , 的长.
49.(2021八上·南充期末)如图,在 中, , 是 边的高.将 边对折,折痕为 ,连接 , 平分 .
(1)求 的度数.
(2)连接 ,求证: .
50.(2021八上·南海期末)我们知道,等腰三角形的两个底角相等,它反映了边与角的转化关系.
如图,△ABC是等腰三角形,AB=AC,我们可以用几何语言表示如下:
∵AB=AC
∴∠B=∠C
如图1,现在有△ABC,点D是AC的中点,E是BC上.一点,将△CDE沿DE折叠到△FDE,连接AF.
(1)设∠DAF=α,∠DCF=β,则∠DFA= ,∠DFC= (结果用含α或β式子表示).
(2)求证:.
(3)如图2,当点E与点B重合时,AB平分∠CAF,若∠AFD=56°,求∠ABD的度数.
2022-2023学年八年级数学上册考点必刷练精编讲义(苏科版)基础
第2章《轴对称图形》
2.2 轴对称的性质
必刷知识点
知识点01:轴对称的性质
轴对称的性质:成轴对称的两个图形中,对应点的连被对称轴垂直平分;成轴对称的两个图形的任何对应部分也成轴对称;成轴对称的两个图形全等.
知识点02:线段的垂直平分线
定义:
垂直并且平分一条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.
知识点01:轴对称的性质
1.(2021八上·宜兴期中)下列结论中不正确的是( )
A.两个关于某直线对称的图形一定全等
B.对称图形的对称点一定在对称轴的两侧
C.两个成轴对称的图形对应点的连线的垂直平分线是它们的对称轴
D.有斜边和一锐角相等的两个直角三角形全等
【答案】B
【完整解答】解:A、两个关于某直线对称的图形一定全等,所以A选项的结论正确;
B、对称图形的对称点可能在对称轴的两侧,也可能都在对称轴上,所以B选项的结论错误;
C、两个成轴对称的图形对应点的连线的垂直平分线是它们的对称轴,所以C选项的结论正确;
D、有斜边和一锐角相等的两个直角三角形全等,所以D选项的结论正确.
故答案为:B.
【思路引导】根据全等图形的概念及轴对称的定义可判断A;对称图形的对称点可能在对称轴的两侧,也可能都在对称轴上,据此判断B;根据轴对称图形的性质可判断C;根据全等三角形的判定定理可判断D.
2.(2021八上·沭阳月考)如图,六边形ABCDEF是轴对称图形, CF 所在的直线是它的对称轴,若∠AFC + ∠BCF = 150°,则∠AFE + ∠BCD 的大小是( )
A.150°B.300°C.210°D.330°
【答案】B
【完整解答】解:∵六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,∠AFC+∠BCF=150°,
∴∠AFC=∠EFC,∠BCF=∠DCF,
∴∠AFE+∠BCD=2(∠AFC+∠BCF)=300°.
故答案为:B.
【思路引导】六边形ABCDEF是轴对称图形,由轴对称的性质可得∠AFC=∠EFC,∠BCF=∠DCF,据此求解.
3.(2021八上·姜堰月考)如图, 内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为15cm,则 的周长为( )
A.5cmB.10cmC.20cmD.15cm
【答案】D
【完整解答】解:∵P点关于OM的轴对称点是G,
∴PA=AG,
∵P点关于ON的轴对称点是H,
∴PB=BH,
∴ 的周长=AP+PB+AB=AG+AB+BH=GH=15cm.
故答案为:D.
【思路引导】由轴对称的性质可得PA=AG,PB=BH,据此不难得到△PAB的周长.
4.(2021八上·江阴月考)下列说法错误的是( )
A.关于某条直线对称的两个三角形一定全等
B.轴对称图形至少有一条对称轴
C.全等的两个三角形一定能关于某条直线对称
D.等腰三角形是轴对称图形
【答案】C
【完整解答】解:A、关于某条直线对称的两个三角形一定全等,故此选项不符合题意;
B、轴对称图形至少有一条对称轴,故此选项不符合题意;
C、两全等三角形不一定关于某条直线对称,故此选项符合题意;
D、等腰三角形是轴对称的图形,故此选项不符合题意.
故答案为:C.
【思路引导】根据轴对称的性质、轴对称图形的定义,逐项进行判断,即可得出答案.
5.(2021八上·陆川期中)下列说法:①全等的两个三角形一定成轴对称;②等腰三角形最少有1条对称轴,最多有3条对称轴;③成轴对称的两个图形一定全等;④任意两条相交直线都组成一个轴对称图形.其中正确的有 .(填序号)
【答案】②③④
【完整解答】解:①全等的两个三角形,不一定构成轴对称的条件,故①不正确;
②等腰三角形最少有1条对称轴,当等腰三角形的三边相等时,有3条对称轴,故②正确;
③成轴对称的两个图形一定全等,故③正确;
④任意两条相交直线都组成一个轴对称图形,故④正确.
故答案为:②③④.
【思路引导】在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫对称轴;轴对称图形(或关于某条直线对称的两个图形)的对应线段相等,对应角相等;根据轴对称的定义和性质并结合各选项可判断求解.
6.(2021八上·沭阳月考)如图, 和 关于直线 对称,若 ,则图中阴影部分的面积为 .
【答案】3
【完整解答】解:由 和 关于直线 对称可得 , ,
阴影部分的面积为 面积的一半
即
故答案为:3.
【思路引导】根据轴对称的性质可得BD=CD=BC,AB=AC,S△BEF=S△CEF,推出S阴影=S△ABC,据此求解.
7.(2021八上·江阴月考)黑板上写着 在正对着黑板的镜子里的像是 .
【答案】
【完整解答】解:根据镜面对称的性质,对着黑板的镜子里的像是
故答案为
【思路引导】根据镜面对称的性质:在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称,即可的查处大案.
8.(2020八上·兴化月考)如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为
【答案】53°
【完整解答】解:∵ ABC与 A′B′C′关于直线l对称,
∴∠C=∠C′=25°,
在 ABC中,∠B=180°﹣∠A﹣∠C=180°﹣102°﹣25°=53°.
故答案为:53°.
【思路引导】根据轴对称的性质可得∠C=∠C′,再根据三角形的内角和等于180°列式计算即可得解.
9.(2018八上·江都月考)如图:有一张直角三角形纸片ABC,∠ACB=90°,∠A=50°,将其沿CD折叠,使点A落在边CB上的点A’处,求∠A’DB的度数。
【答案】证明:∵∠ACB=90°,∠A=50°,
∴∠B=40°,∠CA’D=∠A=50°,
∵∠B+∠A’DB=∠CA’D,
∴∠A’DB=10°.
【思路引导】根据三角形的内角和得出∠B的度数,根据折叠的性质得出 ∠CA'D=∠A=50°, 进而根据三角形的外角定理,由∠A'DB=∠CA'D-∠B即可算出答案。
10.(2019八上·西城期中)下列各图中的单位小正方形的边长都等于1,并且都已经填充了一部分阴影,请再对每个图形进行阴影部分的填充,使得图1成为轴对称图形,使得图2成为至少有4条对称轴且阴影部分面积等于3的图形,使得图3成为至少有2条对称轴且面积不超过6的图形.
【答案】解:如图所示:
【思路引导】根据轴对称的性质解答即可.
11.(2021八上·吉林月考)图①、图②、图③均是4×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,△ABC的顶点均在格点上,在图①、图②、图③中分别画一个与△ABC有一条公共边且与ABC成轴对称的三角形,要求所画三角形不完全重合.
【答案】解:如图①、图②、图③
【思路引导】根据题意,由轴对称的性质,作出图形即可。
12.(2021八上·交城期中)如图,正三角形网格中,已知两个小三角形被涂黑.
(1)再将图中1其余小三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的);
(2)再将图中2其余小三角形涂黑两个,使整个被涂黑的图案构成一个轴对称图形(画出两种不同的).
【答案】(1)解:如图:
(2)解:如图:
【思路引导】(1)根据轴对称图形的含义,判断得到答案即可;
(2)同理,根据轴对称图形的含义,得到答案即可。
13.(2021八上·灌云月考)如图,四边形 与四边形 关于直线 对称.
(1)线段 的对称线段是 , , , .
(2) 与 平行吗?为什么?
(3)若 与 平行则能说明轴对称图形中对称点的连线一定互相平行吗?
【答案】(1);;;
(2)解:∵每对对应点连接成的线段被对称轴垂直平分,即 ,
∴ ;
(3)解: 不一定能说明对称点连线一定互相平行,还有可能共线.
【完整解答】解:(1)根据题意,得线段 的对称线段是 , , , ;
故答案为: , , , ;
【思路引导】(1)根据轴对称的性质即可得出答案;
(2)根据轴对称的性质得出AE⊥MN,BF⊥MN,即可得出AE∥BF;
(3)根据轴对称的性质得出对称点连线不一定互相平行,还有可能共线,即可得出答案.
知识点02:作图—轴对称
14.(2018八上·蔡甸期中)如图,在3×3的正方形的网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中最多能画出( )个格点三角形与△ABC成轴对称.
A.6个B.5个C.4个D.3个
【答案】A
【完整解答】解:如图,可以画6个.
【思路引导】根据轴对称的定义和网格图的特征可画图求解.
15.(2018八上·田家庵期中)如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个.
A.3个B.4个C.5个D.6个
【答案】C
【完整解答】如图所示:
与△ABC成轴对称且以格点为顶点三角形由△ABG、△CDF、△AEF、△DBH,△BCG共5个,
故答案为:C.
【思路引导】根据轴对称的性质进行作答即可。
16.(2021八上·沂水期中)如图,在平面直角坐标系 中, 可以看作是 经过若干次的图形变化(轴对称、平移)得到的,写出一种由 得到 的过程: .
【答案】将 关于y轴对称,再向上平移6个单位长度得到
【完整解答】解:根据题意, 可以看作是先将 关于y轴对称,再向上平移6个单位长度得到的,
故答案为:将 关于y轴对称,再向上平移6个单位长度得到 .
【思路引导】将 关于y轴对称,再向上平移6个单位长度得到的,答案不唯一。
17.(2020八上·兴化月考)如图,在4×4的正方形网格中,有5个小正方形已被涂黑(图中阴影部分),若在其余网格中再涂黑一个小正方形,使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形,则可涂黑的小正方形共有 个.
【答案】4
【完整解答】解:如图所示,有4个小正方形使之成为轴对称图形:
故答案为4
【思路引导】根据轴对称图形的概念、画出图形解答即可.
18.(2019八上·丰南期中)如图,在网格图中选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则把阴影涂在图中标有数字 的格子内.
【答案】3
【完整解答】解:根据轴对称的定义,沿着虚线进行翻折后能够重合,
根据题意,阴影应该涂在标有数字3的格子内;
故答案为3.
【思路引导】根据轴对称的定义,沿着虚线进行翻折后能够重合,所以阴影应该涂在标有数字3的格子内.
19.如图,在平面直角坐标系中,A(0,1),B(3, ),P为x轴上一动点,则PA+PB最小时点P的坐标为 .
【答案】(2,0)
【完整解答】先作出点A关于x轴对称的点A′(0,-1),再连接A′B交x轴于点P,则点P即为所求.
由题中条件设直线A′B的解析式为y=kx+b,可得 ,求出 ,
即直线A′B的解析式为y= x-1,并得到当y=0时,与x轴的交点坐标(2,0).
故答案为:(2,0).
【思路引导】先作出点A关于x轴对称的点A′,再连接A′B交x轴于点P,根据“两点时间,线段最短”,则点P即为所求。用待定系数法求得A′B的解析式,再令y=0,求得点P坐标即可。
20.(2021八上·惠州期末)如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
⑴在图中作出关于y轴对称的;
⑵写出点的坐标(直接写答案);
⑶在y轴上画出点P,使PB+PC最小.
【答案】解:⑴先根据轴对称的性质分别描出点,再顺次连接即可得到,如图所示:
⑶由轴对称的性质得:
则
由两点之间线段最短得:当三点共线时,取得最小值,最小值为
如图,连接,与y轴的交点P即为所求.
【完整解答】解:(2)点坐标关于y轴对称的变化规律:横坐标变为相反数,纵坐标不变
;
【思路引导】(1)根据轴对称性质即可在图中作出三角形ABC关于y轴对称的点;
(2)结合(1)即可写出对应点的坐标;
(3)根据两点之间线段最短即可在y轴上画出点P,使取得最小值。
21.(2021八上·大埔期末)在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
( 1 )请在如图所示的网格平面内作出平面直角坐标系;
( 2 )请作出△ABC关于y轴对称的△A′B′C′;
( 3 )写出点B′的坐标.
【答案】解:
点B′的坐标为(2,1).
【思路引导】(1)根据点的坐标作平面直角坐标系即可;
(2)根据关于y轴对称的点的坐标作三角形即可;
(3)根据平面直角坐标系求出点B'的坐标即可。
22.(2021八上·凤县期末)如图,在直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5),请回答下列问题:
(1)画出△ABC关于x轴的对称图形ΔA1B1C1;直接写出A1、B1、C1的坐标;
(2)如图,在直线 上找一点M,使得AM+BM的值最小.(保留作图痕迹)
【答案】解:(1)如图,△A1B1C1即为所求,
A1(1,-4),B1(4,-2),C1(3,-5);
(2)如图,点M即为所求.
【思路引导】(1)利用关于x轴对称的点的坐标特点:横坐标不变,纵坐标互为相反数可得到点 A1、B1、C1的坐标,再画出△A1B1C1;
(2)利用轴对称的应用-最短问题,作出点A关于直线L的对称点N,连接BN交直线L于点M.:
知识点03:剪纸问题
23.(2021八上·长兴月考)如图,将一张正方形纸片经两次对折,并剪出一个菱形小洞后展开铺平,得到的图形是图中的哪一个( )
A.B.
C.D.
【答案】D
【完整解答】解:动手操作或由图形的对称性,可得应在B、D选项中选择,又观察图可知,菱形小洞靠近正方形的中心,则得到的图形是D.
故答案为:D.
【思路引导】观察图形折叠方法,可得答案.
24.(2021八上·广州期末)如图,把一张长方形的纸,按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC是( )
A.直角三角形B.等边三角形
C.等腰三角形D.等腰直角三角形
【答案】C
【完整解答】解:由题可得,AB与AC可重合,即AB=AC,
∴△ABC是等腰三角形.
故答案为:C.
【思路引导】根据轴对称图形的性质可得答案。
25.(2020八上·洪泽月考)将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上面的爱心,将留下的纸片展开,得到的图形是( )
A. B.
C.D.
【答案】B
【完整解答】解:由图可知:
将折纸展开可得选项B中的图案,
故答案为:B.
【思路引导】对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现.应严格按照所给方式,向上对折,再向右对折,向右下方对折,剪去上面的爱心即可得到答案.
26.如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中有 个不同的四边形.
【答案】4
【完整解答】让三条相等的边互相重合各得到一个平行四边形;让斜边重合还可以得到一个一般的平行四边形.那么能拼出的四边形的个数是4个.
【思路引导】可动手操作拼图后解答.
27.(2021八上·鼓楼月考)剪纸是我国传统的民间艺术.将一张纸片按图中①,②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A.B.C.D.
【答案】A
【完整解答】解:按照图中的顺序,向右对折,向上对折,从斜边处剪去一个直角三角形,从直角顶点处剪去一个等腰直角三角形,展开后实际是从原菱形的四边处各剪去一个直角三角形,从菱形的中心剪去一个正方形,可得:
.
故答案为:A.
【思路引导】根据图中的顺序可得:展开后实际是从原菱形的四边处各剪去一个直角三角形,从菱形的中心剪去一个正方形,据此判断.
28.(2019八上·松山月考)如图,把一个正方形三次对折后沿虚线剪下,得到的图形是( )
A.B.C.D.
【答案】C
【完整解答】解:将图形 按三次对折的方式展开,依次为:
.
故答案为:C.
【思路引导】根据图中指示进行操作,然后展开进行对照即得结论.
29.(2019八上·扬州月考)如图所示,将一个正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去一个三角形和一个形如“ ”的图形,将纸片展开,得到的图形是( )
A.B.C.D.
【答案】D
【完整解答】解:由题意要求折叠,沿虚线剪去一个三角形和一个形如“1”的图形,展开铺平后的图形是D.
故答案为:D.
【思路引导】按照题中要求动手折叠裁剪,展开后观察图形即可作出判断.
30.(2018八上·丹徒月考)将一张正方形纸片按如图1,图2所示的方向对折,然后沿图3中的虚线剪裁得到图形,再将图形的纸片展开铺平,得到的图案是( )
A.B.C.D.
【答案】C
【完整解答】解:严格按照图中的顺序向左下角翻折,向右下角翻折,剪去一个小三角形,小三角形的特征是一边与正方形的边平行,第三个顶点在两条平行线之间,展开后即可得到图形;
故答案为:C.
【思路引导】先剪一个正方形,严格按照图中的顺序去剪,再把剪好的图形展开,观察图形即可作出判断. 也可以根据折叠的性质及图中三角形的形状及位置作出判断.
31.如图所示,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点,把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是( )
A.正三角形B.正方形C.正五边形D.正六边形
【答案】A
【完整解答】解:∵平角∠AOB三等分,
∴∠O=60°,
∵90°﹣60°=30°,
∴剪出的直角三角形沿折痕展开一次得到底角是30°的等腰三角形,
再沿另一折痕展开得到有一个角是30°的直角三角形,
最后沿折痕AB展开得到等边三角形,
即正三角形.
故答案为:A
【思路引导】因∠O=60°,故第一次展开得到的是一个含30°底角的等腰三角形,再展开得到的是含30°的直角三角形,从而可知最后一次展开得到的是等边三角形,此类问题结合动手操作帮助理解。
32.(2017八上·东台月考)如图,将一正方形纸片沿图(1)、( 2)的虚线对折,得到图(3),然后沿图(3)中虚线的剪去一个角,展开得平面图形(4),则图(3)的虚线是( )
A.B.C.D.
【答案】D
【完整解答】由于得到的图形的中间是正方形,那么它的四分之一为等腰直角三角形.
故答案为:D.
【思路引导】本题主要考查剪纸问题,关键培养空间想象能力和动手操作能力.
知识点04:翻折变换(折叠问题)
33.(2021八上·驻马店期末)如图,有一条直的宽纸带,按图折叠,则∠α的度数等于( )
A.50°B.65°C.75°D.80°
【答案】B
【完整解答】解:如图,
根据题意得:BG∥AF,
∴∠FAE=∠BED=50°,
∵AG为折痕,
∴ .
故答案为:B.
【思路引导】利用两直线平行,同位角相等,可求出∠FAD的度数,利用折叠的性质可求出∠α的度数.
34.(2021八上·川汇期末)如图,将的BC边对折,使点B与点C重合,DE为折痕,若,,则( ).
A.45°B.60°C.35°D.40°
【答案】A
【完整解答】解:由折叠得∠B=∠BCD,
∵∠A+∠B+∠ACB=180°,,,
∴65°+2∠B+25°=180°,
∴∠B=45°,
故答案为:A.
【思路引导】由折叠的性质得∠B=∠BCD,然后根据三角形内角和定理可求解.
35.(2021八上·西湖期中)如图,△ABC中,∠A=20°,沿BE将此三角形对折,又沿BA'再一次对折,点C落在BE上的C′处,此时∠C'BD=27°,则原三角形的∠C的度数为( )
A.27°B.59°C.79°D.69°
【答案】C
【完整解答】解:由折叠的性质可知:∠ABE=∠C'BD=27°,∠CBD=∠C'BD=27°,
∴∠ABC=∠ABE+∠C'BD+∠CBD=27°+27°+27°=81°.
在△ABC中,∠A=20°,∠ABC=81°,
∴∠C=180°﹣∠A﹣∠ABC=180°﹣20°﹣81°=79°.
故答案为:C.
【思路引导】由折叠的性质可知:∠ABE=∠C'BD=27°,∠CBD=∠C'BD=27°,然后根据角的和差关系求出∠ABC的度数,接下来根据内角和定理求解即可.
36.(2021八上·沙坪坝期末)如图所示,在 中, ,将 沿边 翻折得到 .若 ,则 的度数为( )
A.50°B.60°C.65°D.70°
【答案】B
【完整解答】解:∵ 沿边 翻折得到 ,
∴∠AEB=∠AEF,
∴∠BEF=2∠AEB,
∵ ,
∴∠BEF=2∠AEB=180°-∠FEC=180°-80°=100°,
∴∠AEB=50°,
∵
∴ =180°-∠B-∠AEB=60°.
故答案为:B.
【思路引导】根据“将 沿边 翻折得到 ”得到∠AEB=∠AEF,即可得到∠BEF=2∠AEB,根据平角的定义可得∠BEF=2∠AEB=100°,从而得到∠AEB=50°,根据三角形内角和即可得到 的度数.
37.(2020八上·无锡月考)经过以下变化后所得到的三角形不能和 全等的是( )
A.B.
C.D.
【答案】D
【完整解答】∵平移、旋转,翻折前后的三角形全等,
∴选项A、B、C不符合题意,
故答案为:D.
【思路引导】根据定义,平移、旋转、翻折后的图形与原图形全等,放大后的图形与原图形相似,由此即可选择.
38.(2021八上·沭阳月考)如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D′、C′的位置处,若∠1=58°,则∠EFB的度数是 .
【答案】61°
【完整解答】解:
由翻折的性质得:∠DED′=2∠DEF,
∵∠1=58°,
∴∠DED′=180°-∠1=122°,
∴∠DEF=61°,
又∵AD∥BC,
∴∠EFB=∠DEF=61°.
故答案为:61°.
【思路引导】由翻折的性质可得:∠DED′=2∠DEF,根据平角的概念可得∠DED′的度数,进而得到∠DEF的度数,然后根据平行线的性质进行求解.
39.(2020八上·通山月考)如图,在三角形纸片中, ,沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,则 的周长等于 .
【答案】9
【完整解答】解:∵BC沿BD折叠点C落在AB边上的点E处,
∴DE=CD,BE=BC,
∵AB=8cm,BC=6cm,
∴AE=AB−BE=AB−BC=8−5=3cm,
∴△ADE的周长=AD+DE+AE,
=AD+CD+AE,
=AC+AE,
=6+3,
=9cm.
故答案为:9.
【思路引导】根据折叠的性质得出DE=CD,BE=BC,然后根据线段间的和差关系求出AE,再把△ADE的周长转化为AC+AE,最后代入数据计算即可.
40.(2019八上·恩施期中)如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF= 度.
【答案】80
【完整解答】解:根据折叠的性质,可得:AD=DF,
∵D是AB边上的中点,
即AD=BD,
∴BD=DF,
∵∠B=50°,
∴∠DFB=∠B=50°,
∴∠BDF=180°﹣∠B﹣∠DFB=80°.
故答案为:80.
【思路引导】根据折叠的性质及中点的定义得出BD=DF,根据等边对等角得出∠DFB=∠B=50°,然后根据三角形的内角和定理即可得出∠BDF的度数.
41.(2021八上·句容期末)如图,在三角形纸片 中, ,折叠该纸片,使点C落在 边上的D点处,折痕 与 交于点E,则折痕 的长为 .
【答案】6
【完整解答】解:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∵折叠该纸片,使点C落在AB边上的D点处,
∴∠CBE=∠ABE=30°,CE=DE,∠ADE=90°,
∴∠A=∠ABE,AE=2CE
∴AE=BE=6,
故答案为:6.
【思路引导】由三角形内角和定理得∠ABC=60°,由折叠得∠CBE=∠ABE=30°,∠A=∠ABE,CE=DE,
∠ADE=90°,推出AE=BE,AE=2CE,据此即可得出答案.
42.(2021八上·毕节期末)如图,在平面直角坐标系中,长方形AOBC的边OB、OA分别在x轴、y轴上,点D在边BC上,将该长方形沿AD折叠,点C恰好落在边OB上的E处.若点 ,点 ,则点D的坐标是 .
【答案】(10,3)
【完整解答】解:∵A(0,8),点B(10,0),
∴OA=BC=8,OB=AC=10,
设BD=a,则CD=8﹣a,
由题意可得,CD=DE=8﹣a,
由对折知,AE=AC=10,
∴ ,
∴BE=OB﹣OE=10﹣6=4,
∵∠DBE=90°,
∴a2+42=(8﹣a)2,
解得a=3,
∴点D的坐标为(10,3),
故答案为:(10,3).
【思路引导】根据A、B的坐标及长方形的性质可得OA=BC=8,OB=AC=10,设BD=a,由折叠的性质可得DE=CD=8﹣a,AE=AC=10,在Rt△AOE中,由勾股定理求出OE=6,可得BE=OB﹣OE=4,在Rt△BDE中,利用勾股定理建立关于a方程,解之即可求出点D坐标.
43.(2022八上·博白期末)如图,将纸片沿折叠,使点落在点处,且平分,平分,若,则的度数为 .
【答案】120°
【完整解答】解:如图,连接AA',
平分 , 平分 ,
, ,
,
,
,
,
沿DE折叠,
, ,
, ,
,
故答案为: .
【思路引导】,连接AA',由角平分线的定义得 , ,利用三角形内角和得 ,即得 ,由三角形内角和得∠A=60°,由折叠性质及三角形外角的性质得 .
44.(2021八上·丹东期末)如图,,点和点分别在边和边上,连接,将沿折叠,点的对应点是,若,则 .
【答案】118°
【完整解答】解:设AB与交于点O,
由折叠性质得:∠=∠BAC=33°,
∵∠2=∠BAC+∠AOE,∠AOE=∠1+∠,
∴∠2=∠BAC+∠1+∠=∠1+66°,即∠1=∠2-66°,
∵∠1+∠2=170°,
∴∠2=118°,
故答案为:118°.
【思路引导】根据折叠的性质可得∠A=∠BAC=33°,再利用三角形的外角的性质可得∠2=∠BAC+∠AOE,∠AOE=∠1+∠A,即可得到∠1=∠2-66°,再结合∠1+∠2=170°,即可得到∠2=118°。
45.(2021八上·浙江月考)如图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求AC和DC的长.
【答案】解:由题意可得 , , ,
根据勾股定理可得: ,
设 ,则 ,
在 中, ,即 ,
解得 ,
即 .
【思路引导】利用折叠的性质可知BC=BC′,CD=C′D,由此可求出AC′的长;再利用勾股定理求出AC的长;设CD=xcm,可表示出AD的长,然后利用勾股定理建立关于x的方程,解方程求出x的值,可得到CD的长.
46.(2021八上·三水期中)如图,折叠矩形的一边 ,使点 落在 边的点 处,已知AB=8cm,BC=10cm,求 的长
【答案】解:∵四边形ABCD为矩形,
∴DC=AB=8cm,AD=BC=10cm,∠B=∠D=∠C=90°,
∵折叠矩形的一边AD,使点D落在BC边的点F处,
∴AF=AD=10cm,DE=EF,
在Rt△ABF中,BF= (cm),
∴FC=BC-BF=4(cm),
设EC= ,则DE= ,EF= ,
在Rt△EFC中,
∵EC2+FC2=EF2,
∴x2+42=(8-x)2,解得x=3,
∴EC的长为 .
【思路引导】由四边形ABCD为矩形,得出DC=AB=8cm,AD=BC=10cm,∠B=∠D=∠C=90°,根据折叠矩形的一边AD,使点D落在BC边的点F处,得出AF的值,利用勾股定理得出BF、FC的值,设EC= ,则DE= ,EF= ,在Rt△EFC中,由EC2+FC2=EF2,即可得出EC的长。
47.(2021八上·温州期中)如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处.求∠1+∠2的度数.
【答案】解:∵将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,
∴∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,
∵∠1+∠2+∠HOG+∠EOF+∠DOE=360°,
∵∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°,
∴∠1+∠2=360 °﹣180°=180°.
【思路引导】根据折叠的性质可得∠B=∠HOG,∠A=∠DOE,∠C=∠EOF,则∠HOG+∠EOF+∠DOE=∠A+∠B+∠C=180°,根据周角的概念可得∠1+∠2+∠HOG+∠EOF+∠DOE=360°,据此求解.
48.(2021八上·牡丹月考)十一国庆节,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.武玥同学在制作手工作品的第一、二个步骤是:
①先裁下了一张长 ,宽 的长方形纸片 ;
②如图,将纸片沿着直线 折叠,点 恰好落在 边上的 处.
请你根据①②步骤计算 , 的长.
【答案】解:∵△ADE由△AFE关于AE对称,
∴△ADE≌△AFE,
∴DE=FE,AD=AF,
∵四边形 是矩形,
∴BC=AD=AF=20cm,AB=CD=16cm,
在Rt△ABF中,由勾股定理: cm,
∴CF=BC-BF=20-12=8cm.
∵四边形ABCD是矩形,
∴∠C=90°.
设CE=x,则DE=EF=16-x,
在Rt△CEF中,由勾股定理: ,代入数据:
(16-x)2=x2+64,
解得:x=6.
∴EC=6cm.
综上所述,线段EC=6cm,CF=8cm.
【思路引导】由轴对称的性质可以得出△ADE≌△AFE,即可得出DE=FE,AD=AF,设CE=x,则DE=EF=16-x,由勾股定理可以求出结论。
49.(2021八上·南充期末)如图,在 中, , 是 边的高.将 边对折,折痕为 ,连接 , 平分 .
(1)求 的度数.
(2)连接 ,求证: .
【答案】(1)解: 是 的对称轴,
, ,
.
是 边的高,
.
平分 ,
.
又 ,
.
.
, .
.
,
,
,
.
(2)证明:
, ,
, .
是等边三角形.
.
.
【思路引导】(1)利用轴对称的性质可证得FA=FC,AE=EC,利用等边对等角可证得∠ECA=∠A,再利用三角形高的定义和角平分线的定义得∠CDE=∠CDB,∠DCE=∠DCB,由ASA证明△CDE≌△CDB,利用全等三角形的性质可推出∠CED=∠CBD,由此可得到∠CBD=2∠A,根据∠A+∠B=90°,可求出∠A的度数;
(2)利用三角形的内角和定理求出∠ACD的度数,利用30°角所对的直角边等于斜边的一半,可证得CD=CF,利用有一个角是60°的等腰三角形是等边三角形,可证得△CFD是等边三角形,利用等边三角形的性质可证得结论.
50.(2021八上·南海期末)我们知道,等腰三角形的两个底角相等,它反映了边与角的转化关系.
如图,△ABC是等腰三角形,AB=AC,我们可以用几何语言表示如下:
∵AB=AC
∴∠B=∠C
如图1,现在有△ABC,点D是AC的中点,E是BC上.一点,将△CDE沿DE折叠到△FDE,连接AF.
(1)设∠DAF=α,∠DCF=β,则∠DFA= ,∠DFC= (结果用含α或β式子表示).
(2)求证:.
(3)如图2,当点E与点B重合时,AB平分∠CAF,若∠AFD=56°,求∠ABD的度数.
【答案】(1)α;90°-α
(2)证明:∵将△CDE沿DE折叠到△FDE,
∴∠CDE=∠EDF=α,
∴∠CDE=∠DAF=α,
∴;
(3)解:同理可得:
∠DAF=∠DFA=56°,
AB平分∠CAF,
∴∠DAB=∠BAF=28°,
∵,
是的垂直平分线,记的交点为
结合对折可得:
记的交点为Q,
∴∠ABD=.
【完整解答】解:(1)∵点D是AC的中点,
∴AD=CD,
∵将△CDE沿DE折叠到△FDE,
∴CD=DF,
∴AD=DF,
∴∠DAF=∠DFA=α,
∴∠CDF=2α,
∵CD=DF,
∴∠DFC=∠DCF= =90°-α,
故答案为:α;90°-α;
【思路引导】(1)由等腰三角形的性质和折叠的性质,求解即可;
(2)由折叠的性质得出∠CDE=∠EDF=α,即可得出结论;
(3)由角平分线的性质求出∠DAB=∠BAF=28°, 由角平分线的性质即可求解。
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析),共27页。试卷主要包含了1 函数,03等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷基础练【6.1函数】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷基础练【6.1函数】(原卷版+解析),共28页。试卷主要包含了1 函数,5小时,这里的“1,9t2;,8m/s2);,3xB.y=8x+0,3升/分钟,则油箱中剩余油量Q,6;等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷基础练【3.2勾股定理的逆定理】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷基础练【3.2勾股定理的逆定理】(原卷版+解析),共23页。试卷主要包含了2 勾股定理的逆定理,5,b=2,c=2,3,0,5﹣4﹣2等内容,欢迎下载使用。












