沪教版八年级数学下学期核心考点+重难点讲练与测试核心考点04特殊的平行四边形(原卷版+解析)

这是一份沪教版八年级数学下学期核心考点+重难点讲练与测试核心考点04特殊的平行四边形(原卷版+解析)，共108页。试卷主要包含了，且∠EAF＝∠B＝60°等内容，欢迎下载使用。

考点一：菱形的性质
考点二：菱形的判定
考点三：菱形的判定与性质
考点四：矩形的性质
考点五：矩形的判定
考点六：矩形的判定与性质
考点七：正方形的性质
考点八：正方形的判定
考点九：正方形的判定与性质
考点考向
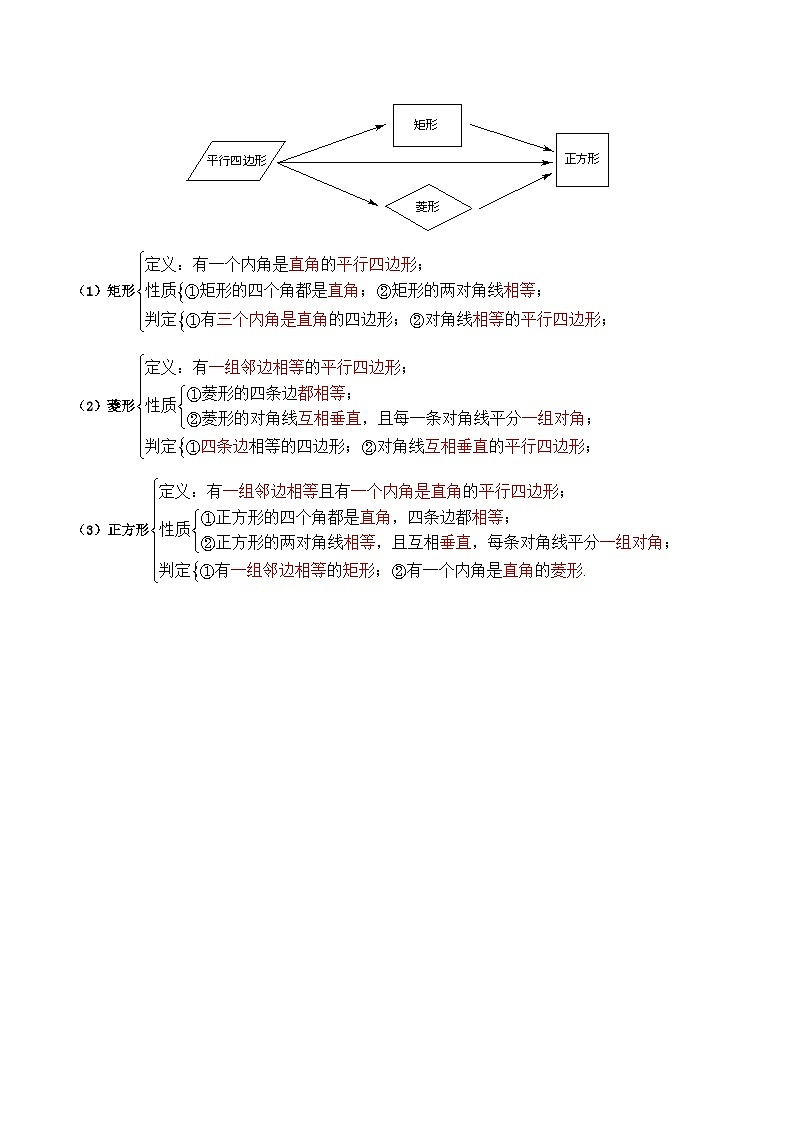
特殊的平行四边形
（1）矩形
（2）菱形
（3）正方形
考点精讲
一．菱形的性质（共7小题）
1．（2022春•青浦区校级期中）如图，菱形ABCD的对角线相交于点O，延长BC至点E，使CE＝BC，联结DE，若∠E＝70°，则∠OBC＝ ．
2．（2022春•杨浦区校级期中）菱形的边长为10厘米，一条对角线为16厘米，它的面积是 平方厘米．
3．（2022春•徐汇区期末）如图，菱形ABCD中，如果AB＝3，BD＝2，那么菱形ABCD的面积为 ．
4．（2022春•上海期中）已知菱形ABCD中，对角线AC＝12，BD＝16，则菱形ABCD的面积是 ．
5．（2022春•虹口区期中）如果菱形的边长为5，相邻两内角的度数之比为1：2，那么该菱形较长的对角线长为 ．
6．（2022春•青浦区校级期中）菱形ABCD中，∠B＝60°，点E、F分别在边BC、CD上，且∠EAF＝60°．求证：AE＝AF．
7．（2022春•杨浦区校级期中）已知：如图菱形ABCD，点E，F分别为边BC，CD上的动点（不与端点重合），且∠EAF＝∠B＝60°．
（1）求证：AE＝AF；
（2）如果AB＝8，设BE＝x，AE＝y，求y与x的函数关系式和定义域；
（3）在（2）的基础上，当x取何值时，S△AEF与S△CEF面积比值为7．
二．菱形的判定（共5小题）
8．（2022春•青浦区校级期中）下列命题是真命题的是（ ）
A．有一组对边平行，另一组对边相等的四边形是平行四边形
B．两条对角线相等的四边形是矩形
C．一条对角线平分一组对角的四边形是菱形
D．对角线互相垂直平分的四边形是菱形
9．（2022春•奉贤区校级期末）如图，直线y＝−x+2与x轴，y轴分别交于点A、B，点C在y轴上，点D为平面内
一点，若四边形ACDB恰好构成一个菱形，请写出点D的坐标 ．
10．（2022春•虹口区期中）如图，△ABC中，AD是∠BAC的平分线，E是AC上一点，AE＝AB，EF∥BC交AD于F，BE与AD交于G．
求证：四边形BDEF是菱形．
11．（2021春•杨浦区期末）如图，已知BD、BE分别是∠ABC与它的邻补角的平分线，AE⊥BE，AD⊥BD，垂足分别为E、D，联结CD、DE，DE与AB交于点O，CD∥AB．求证：四边形OBCD是菱形．
12．（2021春•奉贤区期中）如图，已知在四边形ABCD中，AD∥BC，点E为BC中点，BD⊥DC，EA平分∠DEB．
（1）求证：AE＝DC；
（2）求证：四边形ABED是菱形．
三．菱形的判定与性质（共3小题）
13．（2021春•黄浦区期末）如图，在四边形ABCD中，AD∥BC，BC＝2AD，∠BAC＝90°，点E为BC的中点
（1）求证：四边形AECD是菱形；
（2）联结BD，如果BD平分∠ABC，AD＝2，求BD的长．
14．（2021春•徐汇区期中）如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE＝∠BAD，AE⊥AC
（1）求证：四边形ABDE是平行四边形；
（2）如果DA平分∠BDE，AB＝5，AD＝6，求AC的长．
15．（2021春•普陀区期中）已知，如图，在▱ABCD中，分别在边BC、AD上取两点，使得CE＝DF，连接EF，AE、BF相交于点O，若AE⊥BF．
（1）求证：四边形ABEF是菱形；
（2）若四边形ABEF的周长为16，∠BEF＝120°，求AE的长．
四．矩形的性质（共6小题）
16．（2022春•青浦区校级期中）下面性质中菱形有而矩形没有的是（ ）
A．邻角互补B．对角线互相垂直
C．对角线相等D．对角线互相平分
17．（2022春•杨浦区校级期中）矩形的一条边长是a，两条对角线的夹角为60°，则矩形的另外一条边长等于（ ）
A．aB．aC．a或aD．2a
18．（2022春•长宁区校级期末）如图，矩形ABCD的对角线相交于点O，点E、F分别在OA、OD上，EF∥BC，求证：四边形BCFE是等腰梯形．
19．（2022春•徐汇区期末）如图，将矩形ABCD的边BC延长至点E，使CE＝BD，联结AE交对角线BD于点F，交边CD于点G，如果∠ADB＝38°，那么∠E的大小为 ．
20．（2022春•宝山区校级月考）如图：在直角坐标系里点B（0，4），已知ABDO为矩形，∠DBO＝30°，则点A坐标为 ．
21．（2021春•杨浦区校级期中）如图，矩形ABCD的对角线AC与BD相交于点O，以AO，AB为邻边作平行四边形ABC1O，AC1交OB于点O1；以AO1，AB为邻边作平行四边形ABC2O1…，若S矩形ABCD＝a，则＝ ．
五．矩形的判定（共6小题）
22．（2022春•杨浦区校级期中）下列条件不能判定一个四边形是矩形的是（ ）
A．四个内角都相等
B．四条边都相等
C．对角线相等且互相平分
D．对角线相等的平行四边形
23．（2022春•青浦区校级期中）四边形ABCD的对角线AC、BD互相平分，要使它成为矩形，可添加条件（ ）
A．AB＝CDB．AC＝BDC．AB∥CDD．AC⊥BD
24．（2021春•奉贤区期中）下列说法不正确的是（ ）
A．两组对边分别相等的四边形是平行四边形
B．对角线相等的平行四边形是矩形
C．一个角是直角的四边形是矩形
D．对角线互相平分且垂直的四边形是菱形
25．（2022春•虹口区期中）如图，在四边形ABCD中，点G在边BC的延长线上，CE平分∠BCD，CF平分∠GCD，EF∥BC交CD于点O，点O为CD的中点．
求证：四边形DECF是矩形．
证明：∵CE平分∠BCD，
∴ ＝ ．
∵EF∥BC，
∴ ＝ ．
于是， ＝ ．
同理， ＝ ．
（请继续完成证明过程）
26．（2022春•奉贤区校级月考）如图，已知：在四边形ABCD中，E为边CD的中点，AE与边BC的延长线相交于点F，且AE＝EF，BC＝CF．
（1）求证：四边形ABCD是平行四边形；
（2）当AF＝2BE时，求证：四边形ABCD是矩形．
27．（2022春•静安区期中）已知：如图，在平行四边形ABCD中，点E、F分别是AD、BC的中点，点G、H分别在边AB、CD上，且AG＝CH．
（1）求证：△AGE≌△CHF；
（2）若∠AEG+∠BFG＝90°，求证：四边形EGFH是矩形．
六．矩形的判定与性质（共3小题）
28．（2022春•青浦区校级期中）如图，在Rt△ABC中，∠C＝90°，BC＝6，AC＝8，M为斜边AB上一动点，过点M分别作MD⊥AC于点D，作ME⊥CB于点E，则线段DE的最小值为 ．
29．（2022春•杨浦区校级期中）已知，如图，BE，BD是△ABC中∠ABC的内、外角平分线，AD⊥BD于D，AE⊥BE于点E，延长AE交BC的延长线于点N．
求证：DE＝BN．
30．（2022春•青浦区校级期中）如图，在四边形ABCD的中，AB∥CD，对角线AC，BD相交于点O，且AO＝CO，△OAB是等边三角形．
（1）求证：四边形ABCD是矩形；
（2）若S四边形ABCD＝4，求BD的长．
七．正方形的性质（共5小题）
31．（2022春•静安区期中）如图，正方形ABCD中，延长BC到E，使CE＝CA，AE交CD于F，那么∠AFD＝ ．
32．（2022春•浦东新区校级期中）如图，已知正方形ABCD的边长为5厘米，EG∥AD，点H在边AD上，△CEH的面积为8平方厘米，则FG＝ 厘米．
33．（2022春•杨浦区校级期中）如图，E为正方形ABCD外一点，AE＝AD，BE交AD于点F，则∠BED＝ °．
34．（2022春•浦东新区校级期中）已知正方形ABCD，以CD为边作等边△CDE，则∠ADE的度数是 ．
35．（2022春•上海期中）在正方形ABCD中，边长为8，点P是对角线AC上一点，CP＝2，E是射线AB上一点，联结PE，射线PF⊥PE交直线AD于F，当AC＝CE时，AF＝ ．
八．正方形的判定（共4小题）
36．（2022春•长宁区校级期末）在四边形ABCD中，∠A＝∠B＝∠C＝90°．如果再添加一个条件可证明四边形是正方形，那么这个条件可以是（ ）
A．AB＝BCB．AB＝CDC．AC＝BDD．∠D＝90°
37．（2022春•杨浦区校级期中）下列命题为假命题的是（ ）
A．四个内角相等的四边形是矩形
B．对角线的交点到各边距离都相等的四边形是菱形
C．有两组邻边相等的四边形是平行四边形
D．一组邻边相等的矩形是正方形
38．（2022春•宝山区校级月考）如图，在▱ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．
（1）求证：四边形ABCD是菱形．
（2）若∠AED＝2∠EAD，求证：四边形ABCD是正方形．
39．（2022春•上海期中）如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点N．
（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形ADCE为正方形？给出证明．
九．正方形的判定与性质（共1小题）
40．（2019•杨浦区二模）已知：如图，在△ABC中，AB＝BC，∠ABC＝90°，点D、E分别是边AB、BC的中点，点F、G是边AC的三等分点，DF、EG的延长线相交于点H，连接HA、HC．
求证：（1）四边形FBGH是菱形；
（2）四边形ABCH是正方形．
巩固提升
一、单选题
1．（2022春·上海青浦·八年级校考期中）下面性质中菱形有而矩形没有的是（ ）
A．邻角互补；B．对角线互相垂直；
C．对角线相等；D．对角线互相平分．
2．（2022秋·上海·八年级上外附中校考期末）如图，已知双曲线 经过矩形 边 的中点 且交 于 ，四边形 的面积为 2，则
A．1B．2C．4D．8
3．（2022春·上海杨浦·八年级校考期中）下列条件不能判定一个四边形是矩形的是（ ）
A．四个内角都相等B．四条边都相等
C．对角线相等且互相平分D．对角线相等的平行四边形
4．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图正方形和正方形全等，把点A固定在正方形的中心，当正方形绕点A转动时，两个正方形重叠部分的面积是正方形面积的（ ）
A．B．C．D．
5．（2022春·上海·八年级上海市进才中学校考期中）下列命题不正确的是（ ）．
A．一组对边平行，另一组对边相等的四边形是平行四边形
B．一组对角相等，一组邻角互补的四边形是平行四边形
C．一组对角相等，一组对边平行的四边形是平行四边形
D．对角线互相垂直且相等的平行四边形是正方形
6．（2022秋·上海·八年级阶段练习）如图，在矩形ABCD中，AB＝2，AD＝3，动点P满足S△PBC＝S矩形ABCD，则点P到B，C两点距离之和PB+PC的最小值为（ ）
A．B．C．D．2
二、填空题
7．（2022春·上海奉贤·八年级校考期中）在矩形中∠ABC=90°， 和相交于点，．则的度数等于_____．
8．（2022春·上海·八年级校考期末）如图，矩形的两条对角线相交于点，，，则的长是______．
9．（2022秋·上海杨浦·八年级校考期中）如图，把一张长方形的纸片折叠起来，使其对角顶点A、C重合，若长为，长为，其不重合部分的面积是_______．
10．（2022春·上海青浦·八年级校考期末）如图，▱的对角线、交于点，顺次联结▱各边中点得到的一个新的四边形，如果添加下列四个条件中的一个条件：①；②；③；④，可以使这个新的四边形成为矩形，那么这样的条件可以是______．（填序号）
11．（2022春·上海浦东新·八年级校考期中）如图所示，在中，，，，为上一动点不与、重合，作于点，于点，连接，则的最小值是______．
12．（2022春·上海青浦·八年级校考期末）已知：如图，在中，，，，点位于边上，过点作边的平行线交边于点，过点作边的平行线交边于点，设，四边形的面积为，则关于的函数关系式是______．（不必写定义域）
13．（2022春·上海青浦·八年级校考期中）如图，菱形的对角线相交于点，延长至点，使，连接，若，则________．
14．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图，菱形中，于点E，交于F，若E为中点，且，则F到边的距离为____________．
15．（2022春·上海·八年级校考期中）已知菱形中，对角线，，则菱形的面积是______．
16．（2022春·上海宝山·八年级校考阶段练习）如图，中，已知是的平分线，E、F分别是边的中点，联结，要使四边形为菱形，需要满足一定的条件，该条件可以是______．
17．（2022春·上海浦东新·八年级上海市张江集团中学校考期中）如图，在ABCD和BEFG中，AB＝AD，BG＝BE，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC＝∠BEF＝60°，则________．
18．（2022春·上海·八年级上海市张江集团中学校考期中）如图，在ABCD和BEFG中，AB＝AD，BG＝BE，点A、B、E在同一直线上，P是线段DF的中点，联结PG，PC．若∠ABC＝∠BEF＝60°，则＝________．
19．（2022春·上海青浦·八年级校考期中）如图，平面内直线，且相邻两条平行线间隔均为1，正方形的4个顶点分别在4条平行线上，则正方形的面积为_________．
20．（2022春·上海·八年级校考期中）如图，为正方形外一点，，交于点，则______．
21．（2022春·上海浦东新·八年级校考期中）如图，已知在矩形纸片中，，，点E是的中点，点F是边上的一个动点，将沿所在直线翻折，得到，连接，，则当是以为腰的等腰三角形时，的长是_______________．
22．（2022春·上海·八年级校考期中）在正方形中，边长为，点是对角线上一点，，是射线上一点，联结，射线交直线于，当时，______．
23．（2022春·上海长宁·八年级上海市民办新世纪中学校考期末）如图，四边形中，，，顺次连接四边形各边的中点，得到四边形，再顺次连接四边形各边的中点，得到四边形；…；如此进行下去，得到四边形，那么四边形的周长为________．
三、解答题
24．（2022秋·上海青浦·八年级校考期末）已知：如图，在矩形中，，．对角线的垂直平分线分别交、于点、．求线段的长．
25．（2022春·上海宝山·八年级校考阶段练习）如图，已知梯形中，， 、分别是、的中点，点在边上，且．
(1)求证：四边形是平行四边形；
(2)连接，若平分，求证：四边形是矩形．
26．（2022春·上海·八年级上海同济大学附属存志学校校考期中）如图1，在平行四边形中，的平分线交直线于点E，交直线于点F．
(1)当时，G是的中点，联结（如图2），请直接写出的度数______．
(2)当时，，且，分别联结、（如图3），求的度数．
27．（2022春·上海杨浦·八年级校考期中）已知：如图菱形ABCD，点E，F分别为边BC，CD上的动点（不与端点重合），且∠EAF=∠B=60°．
(1)求证：AE=AF；
(2)如果AB=8，设BE=x，AE=y，求y与x的函数关系式和定义域；
(3)在（2）的基础上，当x取何值时，与面积比值为7．
28．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图，已知平行四边形中，对角线、交于点，是延长线上一点，且是等边三角形．
(1)求证：四边形是菱形；
(2)若，求证：四边形是正方形．
29．（2022春·上海·八年级专题练习）如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．
(1)求证：AD＝EC；
(2)若BC＝2AD，AB＝AO＝m，求证：S四边形ADCE＝m2．（其中S表示四边形ADCE的面积）
30．（2022春·上海·八年级校考阶段练习）如图，已知，，，点在边上，，垂足为点，以为边作正方形，点在边上，且位于点的左侧，联结．
(1)设，，求关于的函数解析式，并写出函数的定义域；
(2)当四边形是等腰梯形时，求的长；
(3)联结，当是等腰三角形时，求正方形的面积．
31．（2022春·上海·八年级校考期中）如图，在中，，，垂足为点是外角的平分线，，垂足为点．
(1)求证：四边形为矩形；
(2)当满足什么条件时，四边形为正方形？给出证明．
32．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图：已知在平面直角坐标系中，是矩形，，，点P是边边上一动点，联结，将四边形沿所在直线翻折，落在的位置，点A、B的对应点分别为点E、F，边与边的交点为点G．
(1)当P坐标为时，求G点坐标，和直线的解析式．
(2)过G作交于H，若；，求y关于x的函数解析式，并写出它的定义域；
(3)联结并延长与线段交于点M，当时以为腰的等腰三角形时求P点坐标．
33．（2022春·上海·八年级上海市张江集团中学校考期末）【探究与应用】我们把平行四边形沿着它的一条对角线翻折，会发现有很多结论．例如：在平行四边形ABCD中，，将△ABC沿直线AC翻折至△AEC，连结DE，则AC∥ED．
(1)如图1，若AD与CE相交于点O，证明以上个结论；
(2)如图2，AD与CE相交于点O，若，，，求△AOC的面积；
(3)如果，，当A、C、D、E为顶点的四边形是正方形时，请画图并求出AC的长；
(4)如果，，当△AED是直角三角形时，直接写出BC的长．
核心考点04 特殊的平行四边形
目录
考点一：菱形的性质
考点二：菱形的判定
考点三：菱形的判定与性质
考点四：矩形的性质
考点五：矩形的判定
考点六：矩形的判定与性质
考点七：正方形的性质
考点八：正方形的判定
考点九：正方形的判定与性质
考点考向
特殊的平行四边形
（1）矩形
（2）菱形
（3）正方形
考点精讲
一．菱形的性质（共7小题）
1．（2022春•青浦区校级期中）如图，菱形ABCD的对角线相交于点O，延长BC至点E，使CE＝BC，联结DE，若∠E＝70°，则∠OBC＝ 20° ．
【分析】直接利用菱形的性质结合等腰三角形的性质得出∠ECD度数，进而得出答案．
【解答】解：∵四边形ABCD是菱形，
∴BC＝DC，AB∥DC，∠ABD＝∠CBD，
∴∠ABC＝∠DCE，
∵CE＝BC，
∴∠E＝∠CDE＝70°，
∴∠ECD＝∠CBA＝180°﹣2×70°＝40°，
∴∠OBC＝×40°＝20°．
故答案为：20°．
【点评】此题主要考查了菱形的性质以及等腰三角形的性质，正确得出∠ECD度数是解题关键．
2．（2022春•杨浦区校级期中）菱形的边长为10厘米，一条对角线为16厘米，它的面积是 96 平方厘米．
【分析】根据菱形的性质得到以及勾股定理求出另一条对角线的长，然后根据菱形的面积公式计算求值．
【解答】解：四边形ABCD是菱形，因为菱形的对角线互相垂直平分，所以OA＝8，OB＝，即BD＝12，
所以菱形的面积为 （平方厘米），
故答案为：96．
【点评】本题主要考查了菱形的性质，解题的关键是菱形的对角线互相垂直平分及勾股定理来解决．
3．（2022春•徐汇区期末）如图，菱形ABCD中，如果AB＝3，BD＝2，那么菱形ABCD的面积为 4 ．
【分析】根据菱形的性质得出BO＝1，利用勾股定理得出OA，进而利用菱形的面积公式解答．
【解答】解：连接AC交BD于点O，
∵四边形ABCD是菱形，
∴BD＝2BO，BD⊥AC，
∵BD＝2，
∴BO＝1，
∵AB＝3，
∴OA＝＝＝2，
∴AC＝2OA＝4，
∴菱形ABCD的面积＝AC•BD＝×4×2＝4，
故答案为：4．
【点评】此题考查菱形的性质，关键是根据菱形的性质得出BO＝2解答．
4．（2022春•上海期中）已知菱形ABCD中，对角线AC＝12，BD＝16，则菱形ABCD的面积是 96 ．
【分析】根据菱形的面积等于对角线乘积的一半即可解决问题．
【解答】解：∵四边形ABCD是菱形，AC＝12，BD＝16，
∴菱形ABCD的面积＝AC×BD＝×12×16＝96；
故答案为：96．
【点评】本题考查了菱形的性质；数据菱形的面积公式是解题的关键．
5．（2022春•虹口区期中）如果菱形的边长为5，相邻两内角的度数之比为1：2，那么该菱形较长的对角线长为 5 ．
【分析】根据已知可得较小的内角为60°，从而得到较短的对角线与菱形的一组邻边组成一个等边三角形，从而可求得较短对角线的长度，然后利用解直角三角形求得较长的对角线即可．
【解答】解：如图所示：∵菱形的边长为5，
∴AB＝BC＝CD＝DA＝5，∠B+∠BAD＝180°，
∵菱形相邻两内角的度数比为1：2，
即∠B：∠BAD＝1：2，
∴∠B＝60°，
∴△ABC是等边三角形，
∴AC＝AB＝5，
∴AO＝AC＝，
∴BO＝AO＝，
∴BD＝2BO＝2×＝5；
故答案为：5．
【点评】本题考查了菱形的性质以及等边三角形的判定方法；熟练掌握菱形的性质，证明三角形是等边三角形是解决问题的关键．
6．（2022春•青浦区校级期中）菱形ABCD中，∠B＝60°，点E、F分别在边BC、CD上，且∠EAF＝60°．求证：AE＝AF．
【分析】连接AC，如图，根据菱形的性质得AB＝BC，而∠B＝60°，则可判定△ABC为等边三角形，得到∠2＝60°，∠1+∠4＝60°，AC＝AB，易得∠ACF＝60°，∠1＝∠3，然后利用“ASA”可证明△AEB≌△AFC，于是得到AE＝AF．
【解答】证明：连接AC，如图，
∵四边形ABCD为菱形，
∴AB＝BC，
∵∠B＝60°，
∴△ABC为等边三角形，
∴∠2＝60°，∠1+∠4＝60°，AC＝AB，
∴∠ACF＝60°，
∵∠EAF＝60°，即∠3+∠4＝60°，
∴∠1＝∠3，
在△AEB和△AFC中，
，
∴△AEB≌△AFC，
∴AE＝AF．
【点评】本题考查了菱形的性质：菱形具有平行四边形的一切性质；菱形的四条边都相等；菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；菱形是轴对称图形，它有2条对称轴，分别是两条对角线所在直线．也考查了全等三角形的判定与性质．
7．（2022春•杨浦区校级期中）已知：如图菱形ABCD，点E，F分别为边BC，CD上的动点（不与端点重合），且∠EAF＝∠B＝60°．
（1）求证：AE＝AF；
（2）如果AB＝8，设BE＝x，AE＝y，求y与x的函数关系式和定义域；
（3）在（2）的基础上，当x取何值时，S△AEF与S△CEF面积比值为7．
【分析】（1）通过证明△ABC和△ADC是等边三角形，可得AB＝AC，∠B＝∠ACD＝60°＝∠BAC，由“ASA”可证△ABE≌△CAF，可得AE＝AF；
（2）由勾股定理可求y与x的函数关系式；
（3）先求△CEF的面积，由面积关系列出方程可求解．
【解答】（1）证明：如图1，连接AC，
∵四边形ABCD是菱形，
∴AB＝BC＝CD＝AD，∠B＝∠D＝60°，
∴△ABC和△ADC是等边三角形，
∴AB＝AC，∠B＝∠ACD＝60°＝∠BAC，
∴∠EAF＝∠BAC＝60°，
∴∠BAE＝∠CAF，
在△BAE和△CAF中，
，
∴△ABE≌△CAF（ASA），
∴AE＝AF；
（2）解：如图2，过点A作AH⊥BC于H，
∵△ABC是等边三角形，AH⊥BC，AB＝8＝BC，
∴BH＝CH＝4，∠BAH＝30°，
∴AH＝4，
∵AE2＝AH2+EH2，
∴y2＝48+（4﹣x）2，
∴y＝（0＜x＜8）；
（3）解：由（1）可知：△ABE≌△CAF，
∴BE＝CF＝x，S△ABE＝S△CAF，
∵S△CEF＝S△ABC+S△ACF﹣S△ACF﹣S△AFE，
∴S△CEF＝×AB2﹣×AE2＝（64﹣x2+8x﹣64）＝（8x﹣x2），
∵S△AEF与S△CEF面积比值为7，
∴S△AEF＝7S△CEF，
∴（x2﹣8x+64）＝7×（8x﹣x2），
∴x＝4±2，
∴当x＝4±2时，S△AEF与S△CEF面积比值为7．
【点评】本题考查了菱形的性质，全等三角形的判定和性质，等边三角形的判定和性质，勾股定理等知识，灵活运用这些性质解决问题是解题的关键．
二．菱形的判定（共5小题）
8．（2022春•青浦区校级期中）下列命题是真命题的是（ ）
A．有一组对边平行，另一组对边相等的四边形是平行四边形
B．两条对角线相等的四边形是矩形
C．一条对角线平分一组对角的四边形是菱形
D．对角线互相垂直平分的四边形是菱形
【分析】利用平行四边形、矩形、菱形及正方形的判定方法分别判断，即可确定正确的选项．
【解答】解：A、有一组对边平行且相等的四边形是平行四边形，是假命题；
B、两条对角线平分且相等的四边形是矩形，是假命题；
C、一条对角线平分一组对角的平行四边形是菱形，是假命题；
D、对角线互相垂直平分的四边形是菱形，是真命题；
故选：D．
【点评】考查了命题与定理的知识，解题的关键是了解平行四边形、矩形、菱形及正方形的判定方法，难度不大．
9．（2022春•奉贤区校级期末）如图，直线y＝−x+2与x轴，y轴分别交于点A、B，点C在y轴上，点D为平面内
一点，若四边形ACDB恰好构成一个菱形，请写出点D的坐标 （2，2）或（2，﹣2） ．
【分析】根据直线y＝−x+2与x轴，y轴分别交于点A、B，求得OA＝OB＝2，根据勾股定理得到AB＝2，根据菱形的性质即可得到结论．
【解答】解：∵直线y＝−x+2与x轴，y轴分别交于点A、B，
∴A（0，2），B（2，0），
∴OA＝OB＝2，
∴AB＝2，
∵四边形ACDB是菱形，
∴AC＝CD＝BD＝AB＝2，
当点C在点A的上面时，
过D作DH⊥y轴于H，
∵AC∥BD，
AC⊥x轴，
∴BD⊥x轴，
∴四边形OBDH是矩形，
∴，
∴CH＝2，
∴DH＝＝2，
∴D（2，2），
当点C在点A的下面时，
同理可得，D（2，﹣2），
故答案为：（2，2）或（2，﹣2）．
【点评】本题考查了菱形的判定，熟练掌握菱形的判定定理是解题的关键．
10．（2022春•虹口区期中）如图，△ABC中，AD是∠BAC的平分线，E是AC上一点，AE＝AB，EF∥BC交AD于F，BE与AD交于G．
求证：四边形BDEF是菱形．
【分析】根据AD是∠BAC的平分线，得出∠CAD＝∠DAE，在△ABD和△ADE中，根据全等三角形的判定得出△ABD≌△ADE和△BAF≌△EAF，得出BD＝DE，BF＝EF，在△BFD和△EDF中，再根据SSS得出△BFD≌△EDF，得出∠BFD＝∠DFE，根据EF∥BC，得出∠DFE＝∠FDC，从而得出∠BFD＝∠BDF，即可得出BF＝BD，从而得出四边形BDEF是菱形．
【解答】证明：∵AD是∠BAC的平分线，
∴∠BAD＝∠DAE，
在△ABD和△ADE中，
，
∴△ABD≌△ADE（SAS），
∴BD＝DE，
同理△BAF≌△EAF（SAS），
∴BF＝EF，
在△BFD和△EDF中，
，
∴△BFD≌△EDF（SSS），
∴∠BFD＝∠DFE，
又∵EF∥BC，
∴∠DFE＝∠FDC，
∴∠BFD＝∠BDF，
∴BF＝BD，
∴BF＝BD＝EF＝DE，
∴四边形BDEF是菱形．
【点评】此题考查了菱形的判定，用到的知识点是全等三角形的判定与性质、角平分线的性质与菱形的判定，判定菱形的方法常用三种方法：①定义；②四边相等；③对角线互相垂直平分．
11．（2021春•杨浦区期末）如图，已知BD、BE分别是∠ABC与它的邻补角的平分线，AE⊥BE，AD⊥BD，垂足分别为E、D，联结CD、DE，DE与AB交于点O，CD∥AB．求证：四边形OBCD是菱形．
【分析】根据已知条件首先证明四边形AEBD是矩形，可得OB＝OD，再证明四边形OBCD是平行四边形，进而可得结论．
【解答】证明：∵BD、BE分别是∠ABC与∠ABF的平分线，
∴∠ABD+∠ABE＝×180°＝90°，
即∠EBD＝90°，
又∵AE⊥BE，AD⊥BD，E、D是垂足，
∴∠AEB＝∠ADB＝90°，
∴四边形AEBD是矩形．
∴OB＝OD，
∴∠OBD＝∠ODB，
∵BD平分∠ABC，
∴∠OBD＝∠DBC，
∴∠ODB＝∠DBC，
∴OD∥BC，
∵CD∥AB，
∴四边形OBCD是平行四边形，
∵OB＝OD，
∴平行四边形OBCD是菱形．
【点评】本题考查了矩形的判定与性质，菱形的判定，解决本题的关键是证明四边形AEBD是矩形．
12．（2021春•奉贤区期中）如图，已知在四边形ABCD中，AD∥BC，点E为BC中点，BD⊥DC，EA平分∠DEB．
（1）求证：AE＝DC；
（2）求证：四边形ABED是菱形．
【分析】（1）由直角三角形斜边中线的性质得到DE＝BE＝CE，再根据角平分线的定义和平行线的性质证得∠DAE＝∠AED，得到AD＝CE，证得明四边形ABCD为平行四边形，由平行四边形的性质即可得到AE＝DC；
（2）由（1）可得AD∥BE，AD＝BE＝DE，根据平行四边形和菱形的判定定理可证得四边形ABED是平行四边形，平行四边形ABED是菱形．
【解答】证明：（1）∵E为BC中点，BD⊥DC，
∴DE＝BC＝BE＝CE，
∵EA平分∠DEB，
∴∠AEB＝∠AED，
∵AD∥BC，
∴AD∥CE，
∴∠DAE＝∠AEB，AD∥CE，
∴∠DAE＝∠AED，
∴AD＝DE，
∴AD＝CE，
∴四边形AECD平行四边形，
∴AE＝DC；
（2）由（1）知，四边形AECD平行四边形，
∴AD∥CE，AD＝CE，
∴AD∥BE，
由（1）知，DE＝BE＝CE，
∴AD＝BE＝DE，
∴四边形ABED是平行四边形，
∴四边形ABED是菱形．
【点评】本题主要考查了平行四边形的性质和判定，菱形的判定，平行线的性质，等腰三角形的性质和判定，根据角平分线的定义、平行线的性质证和等腰三角形的性质和判定证得AD＝DE＝CE是解决问题的关键．
三．菱形的判定与性质（共3小题）
13．（2021春•黄浦区期末）如图，在四边形ABCD中，AD∥BC，BC＝2AD，∠BAC＝90°，点E为BC的中点
（1）求证：四边形AECD是菱形；
（2）联结BD，如果BD平分∠ABC，AD＝2，求BD的长．
【分析】（1）由直角三角形的性质可得AE＝AD＝EC，且AD∥BC，可证四边形AECD是平行四边形，即可得结论；
（2）由角平分线的性质和平行线的性质可得AD＝AB＝CD，可证四边形ABCD是等腰梯形，可得BD＝AC，由勾股定理可求AC的长，即可得BD的长．
【解答】证明：（1）∵∠BAC＝90°，点E为BC的中点，
∴AE＝EC＝BC
∵BC＝2AD，
∴AD＝BC
∴AD＝EC，且AD∥BC，
∴四边形AECD是平行四边形，且AE＝EC，
∴四边形AECD是菱形
（2）如图，
∵AD∥BC，AD＜BC
∴四边形ABCD是梯形，
∵BD平分∠ABD，
∴∠ABD＝∠DBC＝∠ABC
∵AD∥BC，
∴∠ADB＝∠DBC，
∴∠ABD＝∠ADB，
∴AB＝AD
∵四边形AECD是菱形，
∴AD＝DC＝2
∴AB＝DC＝2
∴四边形ABCD是等腰梯形，
∴AC＝BD
∵BC＝2AD＝4．
∴BD＝AC＝＝2
【点评】本题考查了菱形的判定和性质，直角三角形的性质，勾股定理，求证BD＝AC是本题的关键．
14．（2021春•徐汇区期中）如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE＝∠BAD，AE⊥AC
（1）求证：四边形ABDE是平行四边形；
（2）如果DA平分∠BDE，AB＝5，AD＝6，求AC的长．
【分析】（1）由平行四边形的判定定理：两组对边分别平行得到结论；
（2）由角平分线、等量代换得到角相等，由等角对等边得到BD＝AB＝5，根据勾股定理列方程求解．
【解答】（1）证明：∵∠ADE＝∠BAD，
∴AB∥DE，
∵AE⊥AC，BD⊥AC，
AE∥BD，
∴四边形ABDE是平行四边形；
（2）解：∵DA平分∠BDE，
∴∠AED＝∠BDA，
∴∠BAD＝∠BDA，
∴BD＝AB＝5，
设BF＝x，则DF＝5﹣x，
∴AD2﹣DF2＝AB2﹣BF2，
∴62﹣（5﹣x）2＝52﹣x2，
∴x＝，
∴AF＝＝，
∴AC＝2AF＝．
【点评】本题考查了平行四边形的判定和性质，角平分线的性质，勾股定理的应用，解题的关键是利用勾股定理列方程．
15．（2021春•普陀区期中）已知，如图，在▱ABCD中，分别在边BC、AD上取两点，使得CE＝DF，连接EF，AE、BF相交于点O，若AE⊥BF．
（1）求证：四边形ABEF是菱形；
（2）若四边形ABEF的周长为16，∠BEF＝120°，求AE的长．
【分析】（1）由平行四边形的性质得出AD∥BC，AD＝BC，证出AF＝BE，则四边形ABEF是平行四边形，由AE⊥BF，即可得出四边形ABEF是菱形；
（2）由菱形的性质得出AB＝BE＝4，AB∥EF，证出△ABE是等边三角形，得出AE＝AB＝4．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD＝BC，
∵CE＝DF，
∴AF＝BE，
∴四边形ABEF是平行四边形，
又∵AE⊥BF，
∴四边形ABEF是菱形；
（2）解：∵菱形ABEF的周长为16，
∴AB＝BE＝4，AB∥EF，
∴∠ABE＝180°﹣∠BEF＝180°﹣120°＝60°，
∴△ABE是等边三角形，
∴AE＝AB＝4．
【点评】本题考查了菱形的判定与性质、平行四边形的判定与性质、等边三角形的判定与性质等知识；熟练掌握菱形的判定与性质是解题的关键．
四．矩形的性质（共6小题）
16．（2022春•青浦区校级期中）下面性质中菱形有而矩形没有的是（ ）
A．邻角互补B．对角线互相垂直
C．对角线相等D．对角线互相平分
【分析】本题要熟知菱形以及矩形的性质方能解答要对比两者之间的相同点以及不同点．
【解答】解：A、∵平行四边形的邻角互补，
∴矩形的邻角互补．故矩形和菱形的邻角均互补，故不符合题意；
B、菱形对角线互相垂直，矩形的对角线不互相垂直，故符合题意．
C、矩形的对角线相等，菱形的对角线互相垂直且平分，故不符合题意；
D、平行四边形的对角线互相平分，矩形对角线互相平分．故矩形和菱形的对角线互相平分，故不符合题意；
故选：B．
【点评】本题考查了矩形的性质，菱形的性质，掌握矩形和菱形的性质是解题的关键．
17．（2022春•杨浦区校级期中）矩形的一条边长是a，两条对角线的夹角为60°，则矩形的另外一条边长等于（ ）
A．aB．aC．a或aD．2a
【分析】分两种情况讨论：①当矩形的短边为a时，先证明△OAB是等边三角形，根据勾股定理求出另一边长；②当矩形的长边为a时，根据三角函数求出另一边长．
【解答】解：分两种情况讨论：
①当矩形的短边为a时，如图所示：
∵四边形ABCD是矩形，
∴OA＝AC，OB＝BD，AC＝BD，∠ABC＝90°，
∴OA＝OB，
∵∠AOB＝60°，
∴△OAB是等边三角形，
∴OA＝AB＝a，
∴AC＝2a，
∴BC＝＝a；
②当矩形的长边为a时，如图所示：
由①得，tan60°＝＝，
∴AB＝＝；
综上所述：另一条边长为a或a，
故选：C．
【点评】本题考查了矩形的性质、勾股定理的运用以及等边三角形的判定与性质；熟练掌握矩形的性质是解决问题的关键．
18．（2022春•长宁区校级期末）如图，矩形ABCD的对角线相交于点O，点E、F分别在OA、OD上，EF∥BC，求证：四边形BCFE是等腰梯形．
【分析】由矩形的性质可得OB＝OC，再根据相似三角形的判定与性质可得OE＝OF，最后根据全等三角形的判定与性质可得结论．
【解答】证明：∵四边形ABCD是矩形，
∴OB＝OC，
∵EF∥BC，
∴，
∴OE＝OF，
在△BOE和△COF中，
，
∴△BOE≌△COF（SAS），
∴BE＝CF，
∴四边形BCFE是等腰梯形．
【点评】此题考查的是矩形的性质、平行线分线段成比例、全等三角形的判定与性质，掌握其性质定理是解决此题的关键．
19．（2022春•徐汇区期末）如图，将矩形ABCD的边BC延长至点E，使CE＝BD，联结AE交对角线BD于点F，交边CD于点G，如果∠ADB＝38°，那么∠E的大小为 19° ．
【分析】连接AC交BD于O，根据矩形的性质得出AD∥BC，OA＝OC，OB＝OD，AC＝BD，求出OB＝OC，根据等腰三角形的性质和平行线的性质得出∠ADB＝∠OCB＝∠OBC＝38°，求出AC＝CE，根据等腰三角形的性质得出∠E＝∠CAE，再求出∠E即可．
【解答】解：连接AC交BD于O，
∵四边形ABCD是矩形，
∴AD∥BC，
∴∠ADB＝∠OBC，
∵∠ADB＝38°，
∴∠OBC＝38°，
∵四边形ABCD是矩形，
∴OA＝OC，OB＝OD，AC＝BD，
∴OB＝OC，
∴∠OCB＝∠OBC＝38°，
∵CE＝BD，AC＝BD，
AC＝CE，
∴∠E＝∠CAE，
∵∠E+CAE＝OCB＝38°，
∴E＝38°＝19°，
故答案为：19°．
【点评】本题考查了矩形的性质，等腰三角形的性质和三角形的外角性质等知识点，能熟记矩形的性质是解此题的关键，注意：①矩形的对边分别平行，②矩形的对角线互相平分且相等．
20．（2022春•宝山区校级月考）如图：在直角坐标系里点B（0，4），已知ABDO为矩形，∠DBO＝30°，则点A坐标为 （﹣，3） ．
【分析】过A作AE⊥x轴于E，利用矩形的性质和含30°角的直角三角形的性质解答即可．
【解答】解：过A作AE⊥x轴于E，
∵四边形OABD是矩形，
∴AB∥OD，∠AOD＝90°，
∵∠DBO＝30°，
∴∠BOD＝60°，
∴∠AOB＝30°，
∴∠AOE＝60°，
∴∠OAE＝30°，
∵OB＝4，
∴OA＝2，
∴OE＝，AE＝3，
∴A（﹣，3），
故答案为：（﹣，3）．
【点评】本题考查了矩形的性质，关键是利用矩形的性质和含30°角的直角三角形的性质解答．
21．（2021春•杨浦区校级期中）如图，矩形ABCD的对角线AC与BD相交于点O，以AO，AB为邻边作平行四边形ABC1O，AC1交OB于点O1；以AO1，AB为邻边作平行四边形ABC2O1…，若S矩形ABCD＝a，则＝ ．
【分析】先求出平行四边形ABC1O，平行四边形ABC2O1…的面积，探究规律后即可解决问题．
【解答】解：∵四边形ABCD是矩形，四边形ABC1O是平行四边形，
∴，，
∴，
同理可得：平行四边形ABC2O1的面积＝，
平行四边形ABC3O2的面积＝，
…
∴平行四边形ABC2021O2020的面积＝．
故答案为：．
【点评】本题考查平行四边形的性质、矩形的性质等知识，解题的关键是学会从特殊到一般探究规律，利用规律解决问题，属于中考常考题型．
五．矩形的判定（共6小题）
22．（2022春•杨浦区校级期中）下列条件不能判定一个四边形是矩形的是（ ）
A．四个内角都相等
B．四条边都相等
C．对角线相等且互相平分
D．对角线相等的平行四边形
【分析】由矩形的判定和菱形的判定分别对各个选项进行判断即可．
【解答】解：A、四个内角都相等的四边形是矩形，故选项A不符合题意；
B、四条边都相等的四边形是菱形，故选项B符合题意；
C、对角线相等且互相平分的四边形是矩形，故选项C不符合题意；
D、对角线相等的平行四边形是矩形，故选项D不符合题意；
故选：B．
【点评】本题考查了矩形的判定、平行四边形的性质以及菱形的判定等知识，熟练掌握矩形的判定和菱形的判定是解题的关键．
23．（2022春•青浦区校级期中）四边形ABCD的对角线AC、BD互相平分，要使它成为矩形，可添加条件（ ）
A．AB＝CDB．AC＝BDC．AB∥CDD．AC⊥BD
【分析】由平行四边形的判定方法得出四边形ABCD是平行四边形，再由矩形的判定方法即可得出结论．
【解答】解：需要添加的条件是AC＝BD，理由如下：
∵四边形ABCD的对角线AC、BD互相平分，
∴四边形ABCD是平行四边形，
∵AC＝BD，
∴平行四边形ABCD是矩形（对角线相等的平行四边形是矩形）；
故选：B．
【点评】本题考查了矩形的判定、平行四边形的判定与性质；熟练掌握平行四边形的判定与性质以及矩形的判定是解题的关键．
24．（2021春•奉贤区期中）下列说法不正确的是（ ）
A．两组对边分别相等的四边形是平行四边形
B．对角线相等的平行四边形是矩形
C．一个角是直角的四边形是矩形
D．对角线互相平分且垂直的四边形是菱形
【分析】根据平行四边形的判定与性质、矩形的判定、菱形的判定分别对各个选项进行判断即可．
【解答】解：A、∵两组对边分别相等的四边形是平行四边形，
∴选项A不符合题意；
B、∵对角线相等的平行四边形是矩形，
∴选项B不符合题意；
C、∵三个角是直角的四边形是矩形，
∴选项C符合题意；
D、∵对角线互相平分且垂直的四边形是菱形，
∴选项D不符合题意；
故选：C．
【点评】本题考查了矩形的判定、平行四边形的判定与性质以及菱形的判定；熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键．
25．（2022春•虹口区期中）如图，在四边形ABCD中，点G在边BC的延长线上，CE平分∠BCD，CF平分∠GCD，EF∥BC交CD于点O，点O为CD的中点．
求证：四边形DECF是矩形．
证明：∵CE平分∠BCD，
∴ ∠BCE ＝ ∠DCE ．
∵EF∥BC，
∴ ∠BCE ＝ ∠FEC ．
于是， ∠DCE ＝ ∠FEC ．
同理， ∠EFC ＝ ∠DCF ．
（请继续完成证明过程）
【分析】结合条件可证得四边形DECF为平行四边形，再利用角平分线的定义可求得∠ECF为直角，则可证得四边形DECF为矩形．
【解答】证明：∵CE平分∠BCD，
∴∠BCE＝∠DCE，
∵EF∥BC，
∴∠BCE＝∠FEC，
于是，∠DCE＝∠FEC
同理，∠EFC＝∠DCF．
∴OE＝OC，OF＝OC，
∴OE＝OF；
∵点O为CD的中点，
∴OD＝OC，
又OE＝OF，
∴四边形DECF是平行四边形，
∵CE平分∠BCD、CF平分∠GCD，
∴∠DCE＝BCD，∠DCF＝∠DCG
∴∠DCE+∠DCF＝（∠BCD+∠DCG）＝90°，
即∠ECF＝90°，
∴四边形DECF是矩形．
故答案为：∠BCE；∠DCE；∠BCE；∠FEC；∠DCE；∠FEC；∠EFC；∠DCF．
【点评】本题主要考查平行线的性质及矩形的判定，证得OE＝OF，得出四边形DECF是平行四边形是解题的关键，注意角平分线的应用．
26．（2022春•奉贤区校级月考）如图，已知：在四边形ABCD中，E为边CD的中点，AE与边BC的延长线相交于点F，且AE＝EF，BC＝CF．
（1）求证：四边形ABCD是平行四边形；
（2）当AF＝2BE时，求证：四边形ABCD是矩形．
【分析】（1）根据全等三角形的判定和性质得到AD＝CF，∠DAE＝∠CFE，求得AD∥BC，根据平行四边形的判定定理即可得到结论；
（2）根据已知条件得到AE＝BE＝EF，根据等腰三角形的性质得到∠EAB＝∠EBA，∠EBF＝∠F，求得∠ABC＝90°，根据矩形的判定定理即可得到四边形ABCD是矩形．
【解答】（1）证明：∵E为边CD的中点，
∴DE＝CE，
在△ADE与△FCE中，
，
∴△ADE≌△FCE（SAS），
∴AD＝CF，∠DAE＝∠CFE，
∴AD∥CF，
∴AD∥BC，
∵BC＝CF，
∴AD＝BC，
∴四边形ABCD是平行四边形；
（2）证明：∵AE＝EF，AF＝2BE，
∴AE＝BE＝EF，
∴∠EAB＝∠EBA，∠EBF＝∠F，
∴∠ABE+∠EBF＝×180°＝90°，
∴∠ABC＝90°，
∴四边形ABCD是矩形．
【点评】本题考查了平行四边形的判定，矩形的判定，全等三角形的判定和性质，证得△ADE≌△FCE是解题的关键．
27．（2022春•静安区期中）已知：如图，在平行四边形ABCD中，点E、F分别是AD、BC的中点，点G、H分别在边AB、CD上，且AG＝CH．
（1）求证：△AGE≌△CHF；
（2）若∠AEG+∠BFG＝90°，求证：四边形EGFH是矩形．
【分析】（1）根据平行四边形的性质得到∠A＝∠C，AD＝BC，根据线段中点的定义得到AE＝AD，CF＝BC，根据全等三角形的判定定理即可得到结论；
（2）根据平行四边形的性质得到B＝∠D，AD＝BC，AB＝CD，求得DE＝AD，BF＝BC，得到DE＝BF，求得BG＝DH，根据全等三角形的性质得到FG＝EH，EG＝FH，∠AEG＝∠CFH，根据矩形的判定定理即可得到结论．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴∠A＝∠C，AD＝BC，AB＝CD，
∵点E、F分别是AD、BC的中点，
∴AE＝AD，CF＝BC，
∴AE＝DE＝BF＝CF，
∵AG＝CH，
∴AB﹣AG＝CD﹣CH，
即BG＝DH
在△AGE与△CHF中，
，
∴△AGE≌△CHF（SAS）；
（2）证明：∵四边形ABCD是平行四边形，
∴∠B＝∠D，AD＝BC，AB＝CD，
∵点E、F分别是AD、BC的中点，
∴DE＝AD，BF＝BC，
∴DE＝BF，
∵AG＝CH，
∴AB﹣AG＝CD﹣CH，
即BG＝DH，
∴△BFG≌△DEH（SAS）；
∴FG＝EH，
由（1）知△AGE≌△CHF，
∴EG＝FH，∠AEG＝∠CFH，
∴四边形EGFH是平行四边形，
∵∠AEG+∠BFG＝90°，
∴∠CFH+∠BFG＝90°，
∴∠GFH＝90°，
∴四边形EGFH是矩形．
【点评】本题考查了矩形的判定，全等三角形的判定和性质，平行四边形的判定和性质，熟练掌握全等三角形的判定和性质定理是解题的关键．
六．矩形的判定与性质（共3小题）
28．（2022春•青浦区校级期中）如图，在Rt△ABC中，∠C＝90°，BC＝6，AC＝8，M为斜边AB上一动点，过点M分别作MD⊥AC于点D，作ME⊥CB于点E，则线段DE的最小值为 ．
【分析】连接CM，先证明四边形CDME是矩形，得出DE＝CM，当CM垂直AB是最短，再由三角形的面积关系求出CM的最小值，即可得出结果．
【解答】解：连接CM，如图所示：
∵MD⊥AC，ME⊥CB，
∴∠MDC＝∠MEC＝90°，
∵∠ACB＝90°，
∴四边形CDME是矩形，
∴DE＝CM，
∵∠C＝90°，BC＝6，AC＝8，
∴AB＝＝10，
当CM⊥AB时，CM最短，此时△ABC的面积＝AB•CM＝BC•AC，
∴CM的最小值＝＝＝，
∴线段DE的最小值为，
故答案为：．
【点评】本题考查了矩形的判定与性质、勾股定理、直角三角形面积的计算方法；熟练掌握矩形的判定与性质，并能进行推理论证与计算是解决问题的关键．
29．（2022春•杨浦区校级期中）已知，如图，BE，BD是△ABC中∠ABC的内、外角平分线，AD⊥BD于D，AE⊥BE于点E，延长AE交BC的延长线于点N．
求证：DE＝BN．
【分析】利用矩形的判定方法得出∠DBE＝∠ADB＝∠AEB＝90°，再根据全等三角形的判定得出AB＝BN．
【解答】证明：∵BE、BD是△ABC中∠ABC的内、外角平分线，
∴∠DBE＝×180°＝90°，
∵AD⊥BD于D，AE⊥BE于E，
∴∠ADB＝∠AEB＝90°，
则∠DBE＝∠ADB＝∠AEB＝90°，
在△ABE和△NBE中，
，
∴△ABE≌△NBE（ASA），
∴AB＝BN，
∵四边形ADBE是矩形，
∴DE＝AB，
∴DE＝BN．
【点评】此题主要考查了矩形的判定与性质以及全等三角形的判定与性质，一个内角是直角的平行四边形，进一步研究其特有的性质：是轴对称图形、内角都是直角、对角线相等．同时平行四边形的性质矩形也都具有．
30．（2022春•青浦区校级期中）如图，在四边形ABCD的中，AB∥CD，对角线AC，BD相交于点O，且AO＝CO，△OAB是等边三角形．
（1）求证：四边形ABCD是矩形；
（2）若S四边形ABCD＝4，求BD的长．
【分析】（1）证明△AOB≌△COD（ASA），得BO＝DO，AB＝CD，则四边形ABCD是平行四边形，再由等边三角形的性质得OA＝OB，则AC＝BD，即可得出结论；
（2）由等边三角形的性质得AB＝OA＝OB，再由矩形的性质和勾股定理得BC＝AB，然后由矩形的面积求出AB＝2，即可解决问题．
【解答】（1）证明：∵AB∥CD，
∴∠OAB＝∠OCD，
在△AOB和△COD中，
，
∴△AOB≌△COD（ASA），
∴BO＝DO，AB＝CD，
∴四边形ABCD是平行四边形，
∵△OAB是等边三角形，
∴OA＝OB，
∴OA＝OC＝OB＝OD，
∴AC＝BD，
∴平行四边形ABCD是矩形；
（2）解：∵△OAB是等边三角形，
∴AB＝OA＝OB，
∵AO＝CO，
∴AC＝2OA，
∴AC＝2AB，
∵四边形ABCD是矩形，
∴∠ABC＝90°，
∴BC＝＝＝AB，
∵S四边形ABCD＝AB•BC＝AB2＝4，
∴AB2＝4，
∴AB＝＝2，
∴OB＝2，
∴BD＝2OB＝4．
【点评】本题考查了矩形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、等边三角形的性质、勾股定理等知识，熟练掌握矩形的判定与性质是解题的关键．
七．正方形的性质（共5小题）
31．（2022春•静安区期中）如图，正方形ABCD中，延长BC到E，使CE＝CA，AE交CD于F，那么∠AFD＝ 67.5° ．
【分析】根据正方形性质得∠BCD＝90°，AC平分∠BCD，得到∠ACB＝45°，再根据外角的性质和等腰三角形性质得∠E＝22.5°，从而进一步得出∠AFD＝∠CFE＝67.5°．
【解答】解：∵四边形ABCD是正方形，
∴∠BCD＝90°，AC平分∠BCD，
∴∠ACB＝45°，
∵CE＝CA，
∴∠E＝∠CAE，
∴∠E＝22.5°，
∵∠DCE＝90°，
∴∠CFE＝67.5°，
∵∠AFD＝∠CFE＝67.5°，
故答案为：67.5°．
【点评】本题主要考查了正方形性质，掌握正方形的性质的应用是解题关键．
32．（2022春•浦东新区校级期中）如图，已知正方形ABCD的边长为5厘米，EG∥AD，点H在边AD上，△CEH的面积为8平方厘米，则FG＝ 厘米．
【分析】过H作HM⊥EG于M，由四边形ABCD是正方形，EG∥AD，HM⊥EG，可得四边形AEGD、四边形HMGD是矩形，根据△CEH的面积为8平方厘米，有EF•MH+EF•CG＝8，即得EF•CD＝8，可求出EF＝，故FG＝EG﹣EF＝厘米．
【解答】解：过H作HM⊥EG于M，如图：
∵四边形ABCD是正方形，边长为5厘米，
∴AD＝CD＝5厘米，∠A＝∠D＝90°，
∵EG∥AD，HM⊥EG，
∴四边形AEGD、四边形HMGD是矩形，
∴EG＝AD＝5厘米，MH＝DG，
∵△CEH的面积为8平方厘米，
∴EF•MH+EF•CG＝8，
∴EF•（MH+CG）＝8，
∴EF•（DG+CG）＝8，即EF•CD＝8，
又CD＝5，
∴EF＝，
∴FG＝EG﹣EF＝5﹣＝（厘米），
故答案为：．
【点评】本题考查正方形性质及应用，解题的关键是根据△CEH的面积为8平方厘米，列出关于EF的方程，从而求得EF的长度．
33．（2022春•杨浦区校级期中）如图，E为正方形ABCD外一点，AE＝AD，BE交AD于点F，则∠BED＝ 45 °．
【分析】根据正方形的性质和等腰三角形的性质，设∠ABE＝∠AEB＝α，∠BED＝x，则∠AED＝∠ADE＝α+x，再根据三角形内角和定理即可解决问题．
【解答】解：∵四边形ABCD是正方形，
∴AB＝AD，∠BAD＝90°，
∵AE＝AD，
∴AB＝AE，
∴∠ABE＝∠AEB，
∵AE＝AD，
∴∠AED＝∠ADE，
如图，设∠ABE＝∠AEB＝α，∠BED＝x，则∠AED＝∠ADE＝α+x，
在△ABE中，2α+β+90°＝180°，
∴2α+β＝90°，
在△ADE中，2α+β+2x＝180°，
∴90°+2x＝180°，
∴x＝45°，
∴∠BED＝45°．
故答案为：45．
【点评】本题考查了正方形的性质，解决本题的关键是掌握正方形的性质．
34．（2022春•浦东新区校级期中）已知正方形ABCD，以CD为边作等边△CDE，则∠ADE的度数是 30°或150° ．
【分析】图1，图2，当点E在正方形内部和点E在正方形外部时根据正方形的性质和等边三角形的性质就可以求出结论．
【解答】解：如图1，∵四边形ABCD是正方形，
∴AD＝CD，∠DAB＝∠ADC＝90°，
∵△CDE是等边三角形，
∴CD＝DE，∠CDE＝60°，
∴∠ADE＝30°；
如图2，∵四边形ABCD是正方形，
∴AD＝CD，∠DAB＝∠ADC＝90°，
∵△CDE是等边三角形，
∴CD＝DE，∠CDE＝60°，
∴∠ADE＝150°．
综上所述，∠ADE的度数是30°或150°．
故答案为：30°或150°．
【点评】本题考查了正方形的性质的运用，等边三角形的性质的运用及等腰三角形的性质的运用，解答时合理运用等腰三角形的性质是关键．
35．（2022春•上海期中）在正方形ABCD中，边长为8，点P是对角线AC上一点，CP＝2，E是射线AB上一点，联结PE，射线PF⊥PE交直线AD于F，当AC＝CE时，AF＝ 4 ．
【分析】过点P作PM⊥BA于M，过点P作PN⊥DA于N，设PF交AB于K，证明四边形AMPN是正方形，由CP＝2，可得AM＝PM＝＝6＝PN＝AN，即得EM＝AB+BE﹣AM＝10，又PE⊥PF，可得△PMK∽△EMP，得MK＝＝，AK＝AM﹣MK＝，再由△FAK∽△FNP，有＝，可得AF＝4．
【解答】解：过点P作PM⊥BA于M，过点P作PN⊥DA于N，设PF交AB于K，如图：
∵四边形ABCD是正方形，边长为8，
∴∠CAB＝45°，∠ABC＝90°，AB＝8，AC＝8，
∴AM＝PM，
∵∠NAM＝∠PMA＝∠PNA＝90°，
∴四边形AMPN是正方形，
∵AC＝CE，
∴AB＝BE＝8，
∵CP＝2，
∴AP＝AC﹣CP＝6，
∴AM＝PM＝＝6＝PN＝AN，
∴EM＝AB+BE﹣AM＝8+8﹣6＝10，
∵PE⊥PF，
∴∠KPM＝90°﹣∠MPE＝∠PEM，
∵∠PMK＝90°＝∠EMP，
∴△PMK∽△EMP，
∴＝，
∴MK＝＝＝，
∴AK＝AM﹣MK＝6﹣＝，
∵AK∥PN，
∴△FAK∽△FNP，
∴＝，即＝，
∴AF＝4，
故答案为：4．
【点评】本题考查正方形性质及应用，解题的关键是作辅助线，构造直角三角形和相似三角形．
八．正方形的判定（共4小题）
36．（2022春•长宁区校级期末）在四边形ABCD中，∠A＝∠B＝∠C＝90°．如果再添加一个条件可证明四边形是正方形，那么这个条件可以是（ ）
A．AB＝BCB．AB＝CDC．AC＝BDD．∠D＝90°
【分析】先判断四边形ABCD是矩形，由正方形的判定可解决问题．
【解答】解：在四边形ABCD中，
∵∠A＝∠B＝∠C＝90°，
∴四边形ABCD是矩形，
当AB＝BC时，即一组邻边相等时，矩形ABCD为正方形，
故A符合题意，
故选：A．
【点评】本题考查了矩形的判定和性质，正方形的判定等，熟练掌握并能够灵活运用正方形的判定是解决问题的关键．
37．（2022春•杨浦区校级期中）下列命题为假命题的是（ ）
A．四个内角相等的四边形是矩形
B．对角线的交点到各边距离都相等的四边形是菱形
C．有两组邻边相等的四边形是平行四边形
D．一组邻边相等的矩形是正方形
【分析】利用平行四边形、矩形、菱形及正方形的判定方法分别判断，即可确定正确的选项．
【解答】解：A、四个内角相等的四边形是矩形，是真命题；
B、因为对角线分成的四个小三角形的面积相等，且对角线的交点到各边距离都相等，所以四条边都相等，此四边形是菱形，是真命题；
C、有两组邻边相等的四边形是筝形，不是平行四边形，是假命题；
D、一组邻边相等的矩形是正方形，是真命题；
故选：C．
【点评】考查了命题与定理的知识，解题的关键是了解平行四边形、矩形、菱形及正方形的判定方法，难度不大．
38．（2022春•宝山区校级月考）如图，在▱ABCD中，对角线AC、BD交于点O，E是BD延长线上的点，且△ACE是等边三角形．
（1）求证：四边形ABCD是菱形．
（2）若∠AED＝2∠EAD，求证：四边形ABCD是正方形．
【分析】（1）根据对角线互相垂直的平行四边形是菱形．进而利用菱形的判定证明即可；
（2）根据有一个角是90°的菱形是正方形，进而根据菱形和正方形的判定证明即可．
【解答】证明：（1）∵▱ABCD，
∴AO＝OC，
∵△ACE是等边三角形，
∴EO⊥AC （三线合一）
即 BD⊥AC，
∴▱ABCD是菱形；
（2）∵△ACE是等边三角形，∠EAC＝60°
由（1）知，EO⊥AC，AO＝OC
∴∠AEO＝∠OEC＝30°，△AOE是直角三角形
∴∠EAO＝60°，
∵∠AED＝2∠EAD，
∴∠EAD＝15°，
∴∠DAO＝∠EAO﹣∠EAD＝45°，
∵▱ABCD是菱形，
∴∠BAD＝2∠DAO＝90°，
∴菱形ABCD是正方形．
【点评】此题主要考查菱形和正方形的判定，要灵活应用判定定理及等腰三角形的性质、外角的性质定理．
39．（2022春•上海期中）如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点N．
（1）求证：四边形ADCE为矩形；
（2）当△ABC满足什么条件时，四边形ADCE为正方形？给出证明．
【分析】（1）根据矩形的有三个角是直角的四边形是矩形，已知CE⊥AN，AD⊥BC，所以求证∠DAE＝90°，可以证明四边形ADCE为矩形．
（2）根据正方形的判定，我们可以假设当AD＝BC，由已知可得，DC＝BC，由（1）的结论可知四边形ADCE为矩形，所以证得，四边形ADCE为正方形．
【解答】（1）证明：在△ABC中，AB＝AC，AD⊥BC，
∴∠BAD＝∠DAC，
∵AN是△ABC外角∠CAM的平分线，
∴∠MAE＝∠CAE，
∴∠DAE＝∠DAC+∠CAE＝180°＝90°，
又∵AD⊥BC，CE⊥AN，
∴∠ADC＝∠CEA＝90°，
∴四边形ADCE为矩形．
（2）当△ABC满足∠BAC＝90°时，四边形ADCE是一个正方形．
理由：∵AB＝AC，
∴∠ACB＝∠B＝45°，
∵AD⊥BC，
∴∠CAD＝∠ACD＝45°，
∴DC＝AD，
∵四边形ADCE为矩形，
∴矩形ADCE是正方形．
∴当∠BAC＝90°时，四边形ADCE是一个正方形．
【点评】本题是以开放型试题，主要考查了对矩形的判定，正方形的判定，等腰三角形的性质，及角平分线的性质等知识点的综合运用．
九．正方形的判定与性质（共1小题）
40．（2019•杨浦区二模）已知：如图，在△ABC中，AB＝BC，∠ABC＝90°，点D、E分别是边AB、BC的中点，点F、G是边AC的三等分点，DF、EG的延长线相交于点H，连接HA、HC．
求证：（1）四边形FBGH是菱形；
（2）四边形ABCH是正方形．
【分析】（1）由三角形中位线知识可得DF∥BG，GH∥BF，根据菱形的判定的判定可得四边形FBGH是菱形；
（2）连接BH，交AC于点O，利用平行四边形的对角线互相平分可得OB＝OH，OF＝OG，又AF＝CG，所以OA＝OC．再根据对角线互相垂直平分的平行四边形得证四边形ABCH是菱形，再根据一组邻边相等的菱形即可求解．
【解答】证明：（1）∵点F、G是边AC的三等分点，
∴AF＝FG＝GC．
又∵点D是边AB的中点，
∴DH∥BG．
同理：EH∥BF．
∴四边形FBGH是平行四边形，
连接BH，交AC于点O，
∴OF＝OG，
∴AO＝CO，
∵AB＝BC，∠ABC＝90°，
∴四边形FBGH是菱形；
（2）∵四边形FBGH是平行四边形，
∴BO＝HO，FO＝GO．
又∵AF＝FG＝GC，
∴AF+FO＝GC+GO，即：AO＝CO．
∴四边形ABCH是平行四边形．
∵AC⊥BH，AB＝BC，
∴四边形ABCH是正方形．
【点评】本题考查正方形的判定，菱形的判定和性质，三角形的中位线，熟练掌握正方形的判定和性质是解题的关键．
巩固提升
一、单选题
1．（2022春·上海青浦·八年级校考期中）下面性质中菱形有而矩形没有的是（ ）
A．邻角互补；B．对角线互相垂直；
C．对角线相等；D．对角线互相平分．
【答案】B
【分析】根据菱形以及矩形的性质逐项分析判断即可．
【详解】解：A、∵平行四边形的邻角互补，故矩形和菱形的邻角均互补，故不符合题意；
B、菱形对角线互相垂直，矩形的对角线不互相垂直，故符合题意．
C、矩形的对角线相等，菱形的对角线互相垂直且平分，故不符合题意；
D、平行四边形的对角线互相平分，故矩形和菱形的对角线互相平分，故不符合题意；
故选：B．
【点睛】本题考查了矩形的性质，菱形的性质，掌握矩形和菱形的性质是解题的关键．
2．（2022秋·上海·八年级上外附中校考期末）如图，已知双曲线 经过矩形 边 的中点 且交 于 ，四边形 的面积为 2，则
A．1B．2C．4D．8
【答案】B
【分析】利用反比例函数图象上点的坐标，设，则根据F点为AB的中点得到．然后根据反比例函数系数k的几何意义，结合，即可列出，解出k即可．
【详解】解：设，
∵点F为AB的中点，
∴．
∵，
∴，即，
解得：．
故选B．
【点睛】本题考查反比例函数的k的几何意义以及反比例函数上的点的坐标特点、矩形的性质，掌握比例系数k的几何意义是在反比例函数图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|是解答本题的关键．
3．（2022春·上海杨浦·八年级校考期中）下列条件不能判定一个四边形是矩形的是（ ）
A．四个内角都相等B．四条边都相等
C．对角线相等且互相平分D．对角线相等的平行四边形
【答案】B
【分析】根据矩形的判定方法逐一判断即可．
【详解】解：A、四个内角都相等的四边形是矩形，故选项A不符合题意；
B、四条边都相等的四边形是菱形，故选项B符合题意；
C、对角线相等且互相平分的四边形是矩形，故选项C不符合题意；
D、对角线相等的平行四边形是矩形，故选项D不符合题意；
故选：B．
【点睛】本题考查的是矩形的判定，掌握“矩形的判定方法”是解本题的关键．
4．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图正方形和正方形全等，把点A固定在正方形的中心，当正方形绕点A转动时，两个正方形重叠部分的面积是正方形面积的（ ）
A．B．C．D．
【答案】C
【分析】如图，AD与EH交于M，AB与GH交于N，连接AH，AG，根据正方形的性质得AG=AH，∠HAG=90°，∠AHM=∠AGN=45°，再利用等角的余角相等得到∠HAM=∠GAN，则可根据“ASA”判断△HAM≌△GAN，即S△HAM=S△ANG，原式得到S四边形AMHN=S正方形EFGH，然后根据正方形的面积公式求解．
【详解】解：如图，AD与EH交于M，AB与GH交于N，连接AH，AG，
∵点A为正方形EFGH的中心，
∴AG=AH，∠HAG=90°，∠AHM=∠AGN=45°，
∵四边形ABCD为正方形，
∴∠DAB=90°，
∴∠HAM=∠GAN，
在△HAM和△GAN中，
，
∴△HAM≌△GAN（ASA），
∴S△HAM=S△GAN，
∴S四边形AMHN=S△HAM+S△AHN=S△AHN+S△ANG=S△AGH=S正方形EFGH=．
故选：C．
【点睛】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．
5．（2022春·上海·八年级上海市进才中学校考期中）下列命题不正确的是（ ）．
A．一组对边平行，另一组对边相等的四边形是平行四边形
B．一组对角相等，一组邻角互补的四边形是平行四边形
C．一组对角相等，一组对边平行的四边形是平行四边形
D．对角线互相垂直且相等的平行四边形是正方形
【答案】A
【分析】根据平行四边形的判定定理，正方形的判定定理逐项分析判断即可．
【详解】A选项：一组对边平行且相等的四边形是平行四边形，所以本命题说法不正确，符合题意；
B选项：一组对角相等，一组邻角互补的四边形是平行四边形，本命题说法正确，不符合题意；
C选项：一组对角相等，一组对边平行的四边形是平行四边形，本命题说法正确，不符合题意；
D选项：对角线互相垂直且相等的平行四边形是正方形，本命题说法正确，不符合题意.故选A．
【点睛】本题考查了平行四边形的判定，正方形的判定定理，掌握平行四边形与正方形的判定定理是解题的关键．
6．（2022秋·上海·八年级阶段练习）如图，在矩形ABCD中，AB＝2，AD＝3，动点P满足S△PBC＝S矩形ABCD，则点P到B，C两点距离之和PB+PC的最小值为（ ）
A．B．C．D．2
【答案】B
【分析】先由S△PBC＝S矩形ABCD．得出动点P在与BC平行且与BC的距离是1的直线l上，作B关于直线l的对称点E，连接CE，则CE的长就是所求的最短距离．然后在直角三角形BCE中，由勾股定理求得CE的值，即PB＋PC的最小值．
【详解】解：设△PBC中BC边上的高是h．
∵S△PBC＝S矩形ABCD．
∴BC•h＝AB•AD，
∴h＝AB＝1，
∴动点P在与BC平行且与BC的距离是1的直线l上，
如图，作B关于直线l的对称点E，连接CE，则CE的长就是所求的最短距离．
在Rt△BCE中，∵BC＝3，BE＝BA＝2，
∴CE＝，
即PB＋PC的最小值为．
故选：B．
【点睛】本题考查了轴对称−最短路线问题，三角形的面积，矩形的性质，勾股定理，两点之间线段最短的性质．得出动点P所在的位置是解题的关键．
二、填空题
7．（2022春·上海奉贤·八年级校考期中）在矩形中∠ABC=90°， 和相交于点，．则的度数等于_____．
【答案】120°##120度
【分析】根据矩形的性质得出，，，即可得出，根据，得出，即可得出△AOB为等边三角形，得出，即可得出．
【详解】解：∵四边形ABCD为矩形，
∴，，，
∴，
∵，
∴，
∴△AOB为等边三角形，
∴，
∴．
故答案为：120°．
【点睛】本题主要考查了矩形的性质，等边三角形的判定和性质，熟练掌握矩形的性质，是解题的关键．
8．（2022春·上海·八年级校考期末）如图，矩形的两条对角线相交于点，，，则的长是______．
【答案】
【分析】首先证明是等边三角形，可以求得的长，然后利用勾股定理求得的长．
【详解】解：四边形是矩形，
，，，
，
，，
，
是等边三角形，
，
，
则．
故答案是：．
【点睛】本题考查了矩形的性质，等边三角形的性质和判定的应用和勾股定理的应用，解决本题的关键是：矩形的对角线相等且互相平分，属于基础题．
9．（2022秋·上海杨浦·八年级校考期中）如图，把一张长方形的纸片折叠起来，使其对角顶点A、C重合，若长为，长为，其不重合部分的面积是_______．
【答案】##
【分析】设，则，根据矩形的性质和折叠的性质可证明，再由勾股定理求出，继而表示出的面积，即可求解．
【详解】四边形是矩形，长为，长为，
，
，
设，则，
把一张长方形的纸片折叠起来，使其对角顶点A、C重合，
，
，
，
，
在中，由勾股定理得，
即，
解得，
，
其不重合部分的面积为．
故答案为：．
【点睛】本题考查了矩形的性质，折叠的性质，勾股定理，直角三角形的全等判定和性质，熟练掌握知识点是解题的关键．
10．（2022春·上海青浦·八年级校考期末）如图，▱的对角线、交于点，顺次联结▱各边中点得到的一个新的四边形，如果添加下列四个条件中的一个条件：①；②；③；④，可以使这个新的四边形成为矩形，那么这样的条件可以是______．（填序号）
【答案】①②④
【分析】根据顺次连接四边形的中点，得到的四边形形状和四边形的对角线位置、数量关系有关，利用三角形中位线性质可得：当对角线垂直时，所得新四边形是矩形．逐一对四个条件进行判断．
【详解】解：顺次连接四边形的中点，得到的四边形形状和四边形的对角线位置、数量关系有关，利用三角形中位线性质可得：当对角线垂直时，所得新四边形是矩形．
①，
新的四边形成为矩形，符合条件；
②四边形是平行四边形，
，．
，
．
根据等腰三角形的性质可知，
，
新的四边形成为矩形，符合条件；
③四边形是平行四边形，
．
，
．
．
，
四边形是矩形，连接各边中点得到的新四边形是菱形，不符合条件；
④，，
，即平行四边形的对角线互相垂直，
新四边形是矩形，符合条件．
所以①②④符合条件．
故答案为：①②④．
【点睛】本题考查矩形，解题的关键是数量掌握矩形的判断定理．
11．（2022春·上海浦东新·八年级校考期中）如图所示，在中，，，，为上一动点不与、重合，作于点，于点，连接，则的最小值是______．
【答案】
【分析】连接，由勾股定理求出的长，再由矩形的判定与性质求出，然后根据垂线段最短可得时，线段的值最小，再根据面积法求解即可．
【详解】解：如图，连接．
，，，
，
，，，
四边形是矩形，
，
由垂线段最短可得时，线段的值最小，
此时，，
即，
解得．
故答案为：．
【点睛】本题考查了勾股定理，矩形的判定与性质，垂线段最短，以及面积法求线段的长，熟练掌握矩形的判定与性质是解答本题的关键．
12．（2022春·上海青浦·八年级校考期末）已知：如图，在中，，，，点位于边上，过点作边的平行线交边于点，过点作边的平行线交边于点，设，四边形的面积为，则关于的函数关系式是______．（不必写定义域）
【答案】
【分析】连接CD，先证四边形是平行四边形，然后利用勾股定理的逆定理证明是直角三角形，从而可得，进而可得四边形是矩形，设DE=a，利用面积法可用x表示出a，根据矩形面积公式即可得答案．
【详解】解：如图，连接CD，
∵DE//BC，DF//AC，
四边形是平行四边形，
在中，，，，
，，
，
是直角三角形，
，
四边形是矩形，
∴CE=DF，CF=DE
设DE=a，，则CE=DF=6-x，
∵S△ABC=S△ADC+S△BDC，
∴，
∴，
解得：，
∵四边形的面积为，
∴．
故答案为：．
【点睛】本题考查了勾股定理的逆定理、矩形的判定与性质、求函数关系式等知识点，灵活运用勾股定理逆定理得出四边形CEDF是矩形是解答本题的关键．
13．（2022春·上海青浦·八年级校考期中）如图，菱形的对角线相交于点，延长至点，使，连接，若，则________．
【答案】20°
【分析】根据菱形的性质得到BC=CD=CE，求出∠DCE的度数，利用菱形的性质求出∠OBC即可．
【详解】解：∵四边形ABCD是菱形，
∴BC=CD，AB∥CD，
∵，
∴CE=CD，
∴∠CDE=，
∴∠DCE=（180°-2∠E）=40°，
∵AB∥CD，
∴∠ABC=∠DCE=40°，
∴∠OBC=∠ABC=20°，
故答案为：20°．
【点睛】此题考查了菱形的性质，等边对等角求角度，熟记菱形的性质是解题的关键．
14．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图，菱形中，于点E，交于F，若E为中点，且，则F到边的距离为____________．
【答案】
【分析】连接BD，过点F作FG⊥AB于点G，根据菱形的性质及各角之间的关系得出∆ABD是等边三角形，再由含30度角的直角三角形的性质及勾股定理得出EF=，根据角平分线的性质即可得出结论．
【详解】解：如图，连接BD，过点F作FG⊥AB于点G，
∵四边形ABCD为菱形，
∴AB=AD=4，AC平分∠DAB，即∠BAC=∠DAC，
∵BE⊥AD，E为AD中点，
∴AB=DB，AE=2，
∴AB=AD=DB，
∴∆ABD是等边三角形，
∴∠BAD=60°，
∴∠DAC=30°，
∴AF=2EF，
∴，
∴EF=，
∵AC平分∠DAB，BE⊥AD，FG⊥AB，
∴GF=EF=，
即点F到AB边的距离为，
故答案为：．
【点睛】题目主要考查菱形的性质及等边三角形的判定和性质，勾股定理解三角形，角平分线的性质等，理解题意，作出辅助线，综合运用这些知识点是解题关键．
15．（2022春·上海·八年级校考期中）已知菱形中，对角线，，则菱形的面积是______．
【答案】
【分析】根据菱形的面积等于对角线乘积的一半即可解决问题．
【详解】解：四边形是菱形，，，
菱形的面积；
故答案为：．
【点睛】本题考查了菱形的性质；数据菱形的面积公式是解题的关键．
16．（2022春·上海宝山·八年级校考阶段练习）如图，中，已知是的平分线，E、F分别是边的中点，联结，要使四边形为菱形，需要满足一定的条件，该条件可以是______．
【答案】（答案不唯一）
【分析】菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四边相等；③对角线互相垂直平分的四边形是菱形．据此即可求解．
【详解】解：由题意知，可添加：．
则三角形是等腰三角形，
由等腰三角形的性质知，顶角的平分线与底边上的中线重合，
即点D是的中点，
∴是三角形的中位线，
∴， ，
∴四边形是平行四边形，
∵，点E，F分别是的中点，
∴，
∴平行四边形为菱形．
故答案为：、或（答案不唯一）．
【点睛】本题考查了菱形的判定．利用了三角形的中位线的性质和平行四边形的判定和性质、等腰三角形的性质．也可添加或．
17．（2022春·上海浦东新·八年级上海市张江集团中学校考期中）如图，在ABCD和BEFG中，AB＝AD，BG＝BE，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC＝∠BEF＝60°，则________．
【答案】
【分析】延长GP交CD于点H，根据AB＝AD，BG＝BE，得出四边形ABCD和四边形BEFG都是菱形，由菱形的性质证明△DPH≌△FPG，得出DH=GF，进而得出△CHG为等腰三角形，利用等腰三角形的性质得出CP⊥HG，∠PCG=60°，再利用直角三角形的性质，即可求解．
【详解】解：如图，延长GP交CD于点H，
在ABCD和BEFG中，AB＝AD，BG＝BE，
∴四边形ABCD和四边形BEFG都是菱形，
∴CD=CB，GF=GB，CD∥AE，GF∥AE，
∴CD∥GF，
∴∠DHP=∠FGP，
∵∠DPH=∠FPG，DP=FP，
∴△DPH≌△FPG（AAS），
∴DH=GF，PH=PG，
∴DH=GB，
∴CH=CG，
∴CP⊥PG，
∴∠HCG=2∠PCG，
∵∠ABC=60°，
∴∠HCG=180°-∠ABC=120°，
∴∠PCG=60°，
∴∠CGP=30°，
∴CG=2PC，
∴，
∴．
故答案为：
【点睛】本题考查了菱形的的判定与性质，全等三角形的判定与性质等知识，掌握全等三角形的判定与性质，等腰三角形的性质，直角三角形的性质是解决问题的关键．
18．（2022春·上海·八年级上海市张江集团中学校考期中）如图，在ABCD和BEFG中，AB＝AD，BG＝BE，点A、B、E在同一直线上，P是线段DF的中点，联结PG，PC．若∠ABC＝∠BEF＝60°，则＝________．
【答案】
【分析】延长GP交CD于点H，根据AB＝AD，BG＝BE，得出四边形ABCD和四边形BEFG都是菱形，由菱形的性质证明△DPH≌△FPG，得出DH=GF，进而得出△CHG为等腰三角形，利用等腰三角形的性质得出CP⊥HG，∠PCG=60°，再利用直角三角形的性质，即可求解．
【详解】解：如图，延长GP交CD于点H，
在▱ABCD和▱BEFG中，AB＝AD，BG＝BE，
∴四边形ABCD和四边形BEFG都是菱形，
∴CD=CB，GF=GB，CD∥AE，GF∥AE，
∴CD∥GF，
∴∠DHP=∠FGP，
∵∠DPH=∠FPG，DP=FP，
∴△DPH≌△FPG（AAS），
∴DH=GF，PH=PG，
∴DH=GB，
∴CH=CG，
∴CP⊥PG，
∴∠HCG=2∠PCG，
∵∠ABC=60°，
∴∠HCG=180°-∠ABC=120°，
∴∠PCG=60°，
∴∠CGP=30°，
∴CG=2PC，
故答案为：
【点睛】本题考查了菱形的判定与性质，全等三角形的判定与性质等知识，掌握全等三角形的判定与性质，等腰三角形的性质，直角三角形的性质是解决问题的关键．
19．（2022春·上海青浦·八年级校考期中）如图，平面内直线，且相邻两条平行线间隔均为1，正方形的4个顶点分别在4条平行线上，则正方形的面积为_________．
【答案】5
【分析】过C点作直线EF与平行线垂直，与l1交于点E，与l4交于点F．证明△CDE≌△CBF，得CF=1，BF=2．根据勾股定理可求BC2得正方形的面积．
【详解】解：如图，过C点作EF⊥l2，交l1于E点，交l4于F点．
∵l1l2l3l4，EF⊥l2，
∴EF⊥l1，EF⊥l4，
即∠CED=∠BFC=90°．
∵ABCD为正方形，
∴∠BCD=90°．
∴∠DCE+∠BCF=90°．
又∵∠DCE+∠CDE=90°，
∴∠CDE=∠BCF．
在△CDE和△BCF中
，
∴△CDE≌△BCF（AAS），
∴BF=CE=2．
∵CF=1，
∴BC2=12+22=5，
即正方形ABCD的面积为5．
故答案为：5．
【点睛】此题主要考查了正方形的性质和面积计算，根据平行线之间的距离构造全等的直角三角形是关键．
20．（2022春·上海·八年级校考期中）如图，为正方形外一点，，交于点，则______．
【答案】45
【分析】根据正方形的性质和等腰三角形的性质，设∠ABE＝∠AEB＝α，∠BED＝x，则∠AED＝∠ADE＝α＋x，再根据三角形内角和定理即可解决问题．
【详解】解：∵四边形ABCD是正方形，
∴AB＝AD，∠BAD＝90°，
∵AE＝AD，
∴AB＝AE，
∴∠ABE＝∠AEB，
∵AE＝AD，
∴∠AED＝∠ADE，
设∠ABE＝∠AEB＝α，∠BED＝x，则∠AED＝∠ADE＝α＋x，，
在△ABE中，2α＋β＋90°＝180°，
∴2α＋β＝90°，
在△ADE中，2α＋β＋2x＝180°，
∴90°＋2x＝180°，
∴x＝45°，
∴∠BED＝45°．
故答案为：45．
【点睛】本题主要考查了正方形的性质，等腰三角形的性质，解决本题的关键是掌握正方形的性质．
21．（2022春·上海浦东新·八年级校考期中）如图，已知在矩形纸片中，，，点E是的中点，点F是边上的一个动点，将沿所在直线翻折，得到，连接，，则当是以为腰的等腰三角形时，的长是_______________．
【答案】1或
【分析】存在三种情况：当时，连接ED，利用勾股定理可以求得ED的长，可判断三点共线，根据勾股定理即可求解；当时，可以证得四边形是正方形，即可求解；当时，连接EC，FC，证明三点共线，再用勾股定理，即可求解．
【详解】解：①当时，连接ED，如图，
∵点E是的中点，，，四边形是矩形，
∴，
由勾股定理可得，，
∵将沿所在直线翻折，得到，
∴，
∵，
∴，
∴三点共线，
∵，
∴，
设，则，，
在中，，
∴，
解得，
∴；
②当时，如图，
∵，
∴点在线段CD的垂直平分线上，
∴点在线段AB的垂直平分线上，
∵点E是的中点，
∴是AB的垂直平分线，
∴，
∵将沿所在直线翻折，得到，
∴，
∴四边形是正方形，
∴；
综上所述，AF的长为1或．
故答案为：1或．
【点睛】本题考查矩形中的翻折问题，涉及矩形的性质、等腰三角形的性质、正方形的判定和性质、勾股定理，分类讨论思想的运用是解题的关键．
22．（2022春·上海·八年级校考期中）在正方形中，边长为，点是对角线上一点，，是射线上一点，联结，射线交直线于，当时，______．
【答案】4
【分析】过点作于，过点作于，设交于，证明四边形是正方形，由，可得，即得，又，可得（ASA），得，，再由可得．
【详解】解：过点作于，交于点，过点作于，设交于，如图：

四边形是正方形，边长为，
，，，，
，
，
四边形是正方形，
∴四边形是矩形，
∴，
，
，
，
，
，
，
，
在与中
∴（ASA）
∴
∵
∴
，
故答案为：．
【点睛】本题考查正方形性质及判定，全等三角形的性质与判定，等腰直角三角形的性质，勾股定理，解题的关键是作辅助线，构造全等三角形．
23．（2022春·上海长宁·八年级上海市民办新世纪中学校考期末）如图，四边形中，，，顺次连接四边形各边的中点，得到四边形，再顺次连接四边形各边的中点，得到四边形；…；如此进行下去，得到四边形，那么四边形的周长为________．
【答案】
【分析】根据三角形中位线性质定理可得每一次取各边中点，所形成的新四边形周长都为前一个的；并且四边形是平行四边形，即可计算四边形A15B15C15D15的周长，
【详解】解：∵在四边形ABCD中，顺次连接四边形ABCD 各边中点，得到四边形A1B1C1D1，
∴A1D1BD，B1C1BD，C1D1AC，A1B1AC；
∴A1D1B1C1，A1B1C1D1，
∴四边形A1B1C1D1是平行四边形；
根据中位线的性质知，A1B1=AC；B1C1=BD
四边形A1B1C1D1周长为
同理，四边形A3B3C3D3是平行四边形，A3B3C3D3周长为
同理，四边形的周长是

四边形A15B15C15D15周长为
故答案为．
【点睛】本题考查了三角形的中位线性质定理：三角形的中位线平行于第三边，并且等于第三边的一半．
三、解答题
24．（2022秋·上海青浦·八年级校考期末）已知：如图，在矩形中，，．对角线的垂直平分线分别交、于点、．求线段的长．
【答案】
【分析】根据线段垂直平分线上的点到线段两端点的距离相等的性质可得，设，表示出的长度，然后在中，利用勾股定理列式计算即可得解．
【详解】解：连接，如图所示：
∵四边形是矩形，
∴，
∵是的垂直平分线，
∴，
设，则 ，
在中，
即
解得：x=52，
∴
【点睛】本题考查了矩形的性质、勾股定理、线段垂直平分线上的点到线段两端点的距离相等的性质；熟练掌握勾股定理和矩形的性质是解题的关键．
25．（2022春·上海宝山·八年级校考阶段练习）如图，已知梯形中，， 、分别是、的中点，点在边上，且．
(1)求证：四边形是平行四边形；
(2)连接，若平分，求证：四边形是矩形．
【答案】(1)见解析
(2)见解析
【分析】（1）连接EG，根据题意得，，根据，可得四边形是平行四边形，则，，根据是的中点得，可得，，即可得；
（2）连接，将与的交点记为点O，根据平分得，根据得，即可得，，根据四边形是平行四边形得，，可得，即可得．
（1）
证明：如图所示，连接EG，
∵梯形中，， 、分别是、的中点，
∴，，
∵，
∴，
∴四边形是平行四边形，
∴，，
∵是的中点，
∴，
∴，，
∴四边形是平行四边形；
（2）
解：如图所示，连接，将与的交点记为点O，
∵平分，
∴，
∵，
∴，
∴，
∴，
∵四边形是平行四边形，
∴，，
∴，
∴平行四边形是矩形．
【点睛】本题考查了矩形的判定，平行四边形的判定，梯形的中位线定理，平行线的性质，角平分线，解题的关键是掌握这些知识点，添加合适的辅助线．
26．（2022春·上海·八年级上海同济大学附属存志学校校考期中）如图1，在平行四边形中，的平分线交直线于点E，交直线于点F．
(1)当时，G是的中点，联结（如图2），请直接写出的度数______．
(2)当时，，且，分别联结、（如图3），求的度数．
【答案】(1)45°
(2)60°
【分析】（1）连接CG，BG，证△DCG≌△BEG（SAS），得到BG=DG，∠CDG=∠EBG，再证△BGD是直角三角形，即得△BGD是等腰直角三角形，即可由等腰直角三角形的性质求解；
（2）延长AB、FG相交于H，连接DH，先证四边形ADFH是平行四边形，再证平行四边形ADFH是菱形，得∠HDF=∠ADF=60°，△DGF≌△DBH（SAS），得∠GDF=∠BDH，即可得∠BDG=∠HDF，可求解．
（1）
解：∵平行四边形，，
∴四边形为矩形，
∴∠ABC=∠BAD=∠BCD=90°，AB=CD，
∴∠ECF=90°，
连接CG，BG，如图2，
∵G是EF的中点，
∴CG=EG=GF，
∵AE平分∠BAD，
∴∠BAE=45°，
∴∠BAE=∠BEA=45°，
∴BE=AB，
∴BE=CD，
∴∠FEC=∠BEA=45°，
∴∠BEG=135°，
∴∠EFC=∠FEC=45°，
∴∠GCF=∠EFC=45°，
∴∠DCG=135°，
∴∠DCG=∠BEF，
在△DCG和△BEG中，
，
∴△DCG≌△BEG（SAS），
∴BG=DG，∠CDG=∠EBG，
∵∠CDG+∠GDB+∠CBD=90°，
∴∠EBG+∠GDB+∠CBD=90°，
∴∠BGD=90°，
∴△BGD是等腰直角三角形，
∴∠BDG=45°；
故答案为：45°；
（2）
解：延长AB、FG相交于H，连接DH，如图，
∵FGCE，
∴ADHF，
∵AHDF，
∴四边形ADFH是平行四边形，
∵∠ABC=120°，
∴∠DAB=60°，∠ADC=∠ABC=120°，
∵AF平分∠DAB，
∴∠BAF=∠DAF=30°，
∵AHDF，
∴∠DFA=∠BAF=∠DAF=30°，
∴DA=DF，∠AEB=∠FEC=30°，
∴平行四边形ADFH是菱形，CE=CF，
∴∠HDF=∠ADF=60°，
∵FG=CE，CE=CF，CF=BH，
∴FG=HB，
在△DGF和△DBH中，
，
∴△DGF≌△DBH（SAS），
∴∠GDF=∠BDH，
∴∠BDG=∠HDF=60°．
【点睛】本题考查平行四边形的性质和判定，矩形的判定与性质，菱形的判定与性质，全等三角形的判定与性质，直角三角形的性质，等腰三角形的判定与性质，本题属四边形综合题目，熟练掌握平行四边形的性质，矩形的判定与性质，菱形的判定与性质是解题的关键．
27．（2022春·上海杨浦·八年级校考期中）已知：如图菱形ABCD，点E，F分别为边BC，CD上的动点（不与端点重合），且∠EAF=∠B=60°．
(1)求证：AE=AF；
(2)如果AB=8，设BE=x，AE=y，求y与x的函数关系式和定义域；
(3)在（2）的基础上，当x取何值时，与面积比值为7．
【答案】(1)见解析
(2)y=（0＜x＜8）
(3)当x=4±2时，与面积比值为7
【解析】（1）
证明：如图1，连接AC，
∵四边形ABCD是菱形，
∴AB=BC=CD=AD，∠B=∠D=60°，
∴△ABC和△ADC是等边三角形，
∴AB=AC，∠B=∠ACD=60°=∠BAC，
∴∠EAF=∠BAC=60°，
∴∠BAE=∠CAF，
在△BAE和△CAF中，
，
∴（ASA），
∴AE=AF；
（2）
解：如图2，过点A作AH⊥BC于H，
∵△ABC是等边三角形，AH⊥BC，AB=8=BC，
∴BH=CH=4，∠BAH=30°，
∴AH=，
∵，
∴，
∴y=（0＜x＜8）；
（3）
解：由（1）可知：，
∴BE=CF=x，，
∵，
∴，
∵与面积比值为7，
∴，
∴，
∴，
∴当时，与面积比值为7．
【点睛】本题考查了全等三角形的性质与判定，勾股定理，函数关系式，解一元二次方程，掌握以上知识是解题的关键．
28．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图，已知平行四边形中，对角线、交于点，是延长线上一点，且是等边三角形．
(1)求证：四边形是菱形；
(2)若，求证：四边形是正方形．
【答案】(1)证明见解析
(2)证明见解析
【分析】（1）根据对角线互相垂直的平行四边形是菱形．由四边形是平行四边形，可得．又由是等边三角形，可得．根据三线合一，对角线垂直，即可得四边形既为菱形；
（2）根据有一个角是的菱形是正方形．由题意易得，所以四边形是菱形，，即四边形是正方形．
【详解】（1）证明：四边形是平行四边形，
是等边三角形，
，
，
四边形是菱形；
（2）证明：由（1）得：是直角三角形，
，
是等边三角形，
，
，
，
，
，
四边形是菱形，
，
四边形是正方形．
【点睛】本题主要考查菱形和正方形的判定，涉及知识点较多，综合性强，能力要求全面，灵活运用正方形和菱形的判定方法是解决问题的关键．
29．（2022春·上海·八年级专题练习）如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，连接EC．
(1)求证：AD＝EC；
(2)若BC＝2AD，AB＝AO＝m，求证：S四边形ADCE＝m2．（其中S表示四边形ADCE的面积）
【答案】(1)证明见解析；
(2)证明见解析
【分析】（1）由，，可证得四边形为平行四边形，又由是边上的中线，可得，即可证得四边形 是平行四边形，继而证得结论；
（2）由，易得四边形 是菱形，继而求得．
(1)
证明：，，
四边形为平行四边形，
，
，
，
四边形是平行四边形，
；
(2)
解：，，
，
四边形 是平行四边形，
四边形 是菱形，
，，
．
【点睛】本题考查了平行四边形的判定与性质以及菱形的判定与性质．注意证得四边形是平行四边形是关键．
30．（2022春·上海·八年级校考阶段练习）如图，已知，，，点在边上，，垂足为点，以为边作正方形，点在边上，且位于点的左侧，联结．
(1)设，，求关于的函数解析式，并写出函数的定义域；
(2)当四边形是等腰梯形时，求的长；
(3)联结，当是等腰三角形时，求正方形的面积．
【答案】(1)，定义域为：
(2)
(3)或
【分析】（1）在中，利用勾股定理，求出关于的函数解析式，根据，求出的定义域；
（2）根据四边形是等腰梯形时，为等腰直角三角形，，列式计算即可；
（3）分和两种情况进行讨论，当，利用三线合一，得到：，列式求解；当，在中，用勾股定理进行求解即可．
【详解】（1）解：∵，，
∴，
∵，
∴，
∴是等腰直角三角形，
∴，
又∵四边形为正方形，
∴，
∴，
在中：，
即：．
∵，
即：，
解得：；
∴，定义域为：；
（2）解：如图：当四边形是等腰梯形时，
，
则：为等腰直角三角形，
∴，
即：，
解得：；
∴的长为：；
（3）解：∵点在内部，
∴，分两种情况讨论是等腰三角形．
①当时，
∵，
∴．
即：．解得．此时．
②当时，．
在中，由勾股定理，得
即：，解得，
∴．
综上，正方形的面积为：或．
【点睛】本题考查等腰三角形的判定和性质，正方形的性质，勾股定理．熟练掌握等腰三角形的判定和性质，是解题的关键．注意，分类讨论．
31．（2022春·上海·八年级校考期中）如图，在中，，，垂足为点是外角的平分线，，垂足为点．
(1)求证：四边形为矩形；
(2)当满足什么条件时，四边形为正方形？给出证明．
【答案】(1)证明见解析；
(2)当满足时，四边形是一个正方形，证明见解析
【分析】（1）根据等腰三角形的性质得出，根据是外角的平分线，得出，进而得出，根据，得出，根据矩形的判定定理即可判定四边形为矩形；
（2）根据题意证明可得四边形为正方形，继而可得当满足，即可求解．
【详解】（1）证明：在中，，
∴，
∵是外角的平分线，
∴，
∴，
又∵，
∴，
∴四边形为矩形.
（2）当满足时，四边形是一个正方形.
理由：∵，
∴，
∵，
∴，
∴，
∵四边形为矩形，
∴矩形是正方形.
∴当时，四边形ADCE是一个正方形．
【点睛】本题考查了矩形的判定，等腰三角形的性质，正方形的判定，综合运用以上知识是解题的关键．
32．（2022春·上海·八年级上海市泗塘中学校考阶段练习）如图：已知在平面直角坐标系中，是矩形，，，点P是边边上一动点，联结，将四边形沿所在直线翻折，落在的位置，点A、B的对应点分别为点E、F，边与边的交点为点G．
(1)当P坐标为时，求G点坐标，和直线的解析式．
(2)过G作交于H，若；，求y关于x的函数解析式，并写出它的定义域；
(3)联结并延长与线段交于点M，当时以为腰的等腰三角形时求P点坐标．
【答案】(1)G（，2），y=−x+12
(2)（0≤x≤3）
(3)P（，2）或（1，2）．
【分析】（1）设PG=a，先求出GD=3a，再根据勾股定理求出点G的坐标，由点C的坐标可求出直线CF的解析式；
（2）由折叠的性质得出DG=5-（5-y）-x=y-x，利用勾股定理得出；
（3）分两种情况解答：①当MG=MP时，得到△APO≌△DGC，由AP=DG，得到，求解即可；②当MG=PG时，先得出△AOP，△DPC，△OPC均为直角三角形，利用勾股定理得到AP2+AO2+DP2+CD2=BC2，列出关于x的方程，得出结果．
（1）
解：（1）设PG=a，
∵四边形OADC是矩形，
∴AD∥OC，
∴∠GPC=∠PCO，
由折叠得：∠PCO=∠PCG，
∴∠PCG=∠GPC，
∴PG=GC=a，
∵OA=2，OC=5，P（2，2），
∴PD=5-2=3，
∴GD=3-a，
在Rt△GDC中，GD2+DC2=CG2，
∴22+（3-a）=a2，
∴a=PG=，
∴AG=2+=，
∴G（，2），
∵C（5，0），
设直线CF为：y=kx+b，则
，解得：，
∴直线CF为：y=−x+12，
∴G（，2）．
（2）
解：∵P（x,2），H（y，0），
由对称性可知：∠OCP=∠FCP，OC=CF，
∵GH⊥PC，
∴CG=CH，
∴FG=OH=y,AP=x,
∴CG=CF-FG=5-y,
∴PG=5-y，
∴DG=5-（5-y）-x=y-x，
在Rt△DGC中，CD2+DG2=CG2，
∴（y-x）2+22=（5-y）2，
∴，
当CF与CD重叠时，G与D重合，此时AP=5-2=3，
∴（0≤x≤3）．
（3）
解：∵△PGM时以MG为腰的等腰三角形，MG=MP或MG=PG，
①当MG=MP时，∠MPG=∠MGP，∠APO=∠MPG，∠MGP=∠DGC，
∴∠APO=∠DGC，
在△APO与△DGC中，
，
∴△APO≌△DGC（AAS），
∴AP=DG，
∴y=2x，
∴
∴3x2-20x+21=0，
∴，
∵（舍去），
∴；
②当MG=PG时，∠MPG=∠PMG，∠MOC=∠MPG，
∴CM=CO，
∵∠OCP=∠MCP，
∴∠OPC=∠MPC=90°，
∴CP⊥OP，
∴△AOP，△DPC，△OPC均为直角三角形，
∴AP2+AO2=OP2，PD2+CD2=CP2，OP2+CP2=OC2，
∴AP2+AO2+DP2+CD2=BC2，
∴x2+22+（5-x）2+22=52，
∴x2-5x+4=0，解得：x=1或x=4＞3（舍去），
综上，AP为或1，
∴P（，2）或（1，2）．
【点睛】本题考查了全等三角形的判定与性质，一次函数的应用，勾股定理等知识点，分类讨论是解题的关键．
33．（2022春·上海·八年级上海市张江集团中学校考期末）【探究与应用】我们把平行四边形沿着它的一条对角线翻折，会发现有很多结论．例如：在平行四边形ABCD中，，将△ABC沿直线AC翻折至△AEC，连结DE，则AC∥ED．
(1)如图1，若AD与CE相交于点O，证明以上个结论；
(2)如图2，AD与CE相交于点O，若，，，求△AOC的面积；
(3)如果，，当A、C、D、E为顶点的四边形是正方形时，请画图并求出AC的长；
(4)如果，，当△AED是直角三角形时，直接写出BC的长．
【答案】(1)证明见解析；
(2)；
(3)或2；图形见解析；
(4)或或
【分析】（1）由平行四边形的定义可得AD∥BC， AD=BC，由折叠的性质可得∠ACB=∠ACE，BC=CE，于是可得△OAC、△ODE是等腰三角形，利用对顶角相等求得∠OCA和∠OED即可证明；
（2）设OD=x，由（1）解答可得OD=OE=x，由折叠的性质可得OC=2-x，由∠B=90°可得ABCD是矩形，Rt△ODC中由勾股定理建立方程求得x，进而求得OA即可解答；
（3）分∠ACB=45°和∠ACB=90°两种情况作出图形，再根据正方形的性质计算求值即可；
（4）分∠ACB=60°，∠ACB=90°和∠ACB=30°，三种情况，根据30°直角三角形的边长关系和勾股定理计算求值即可；
【详解】（1）证明：∵ABCD是平行四边形，
∴AD∥BC，AB=CD，AD=BC，
∴∠OAC=∠ACB，
∵∠ACB=∠ACE，
∴∠OAC=∠OCA，
∴OA=OC，∠OCA=（180°-∠AOC），
∵BC=CE，BC=AD，
∴AD=CE，
∴AD-OA= CE-OC，
∴OE=OD，
∴∠OED=（180°-∠EOD），
∵∠AOC=∠EOD，
∴∠OCA=∠OED，
∴AC∥DE；
（2）解：设OD=x，
由（1）解答可得OD=OE=x，
∵CE=CB=2，
∴OC=2-x，
∵四边形ABCD是平行四边形，∠B=90°，
∴四边形ABCD是矩形，
∴CD=AB=，AD=BC=2，∠ADC=90°，
Rt△ODC中，OC2=OD2+CD2，
∴（2-x）2=x2+2，
∴x=，
∴OA=AD-OD=，
∴△OAC面积=OA•CD=；
（3）解：①如图，∠ACB=45°时，∠B=45°，AB=AC，
∵四边形ABCD是平行四边形，∠B=45°，则∠BCD=135°，
∴∠ACD=90°，
∵∠BAC=180°-∠B-∠ACB=90°，AC∥ED，
∴∠AED=90°，∠CDE=90°，
∴四边形ACDE是矩形，
∵AB=AC=AE，
∴四边形ACDE是正方形，
∵CE=CB=2，
∴AC2+AE2=CE2，
∴AC=；
②如图，∠ACB=90°时，∠B=∠BAC=45°， CA=CB，
∵四边形ABCD是平行四边形，∠B=45°，则∠BAD=135°，
∴∠CAD=90°，
∵AC∥ED，∴∠ADE=90°，∠CED=90°，
∴四边形ACDE是矩形，
∵BC=CE=CA，
∴四边形ACDE是正方形，
∴AC=2；
∴AC=或2；
（4）解：①如图，∠ACB=60°时，
∠B=30°，则∠BAC=90°，
∴∠CAE=90°，
∵AC∥DE，∴∠AED=90°，则△AED是直角三角形，
Rt△ABC中，AB=3，BC=2AC，
∴BC2=AB2+AC2=9+BC2，
BC=；
②如图，∠ACB=90°时，
∵四边形ABCD是平行四边形，∠B=30°，则∠BAD=150°，
∵∠BAC=90°-∠B=60°，∴∠CAD=90°，
∵AC∥DE，∴∠ADE=90°，则△AED是直角三角形，
Rt△ABC中，AB=3，AC=，
∴BC==，
③如图，∠ACB=30°时，作AH⊥BC于点H，
由四边形ABCD是平行四边形得AD∥BC，
∴∠DAC=∠ACB=30°，
∴∠BAC=180°-∠B-∠ACB=120°，
由折叠的性质可得∠EAC=∠BAC=120°，
∴∠EAD=∠EAC-∠DAC=90°，则△AED是直角三角形，
Rt△ABH中，AB=3，AH=，
∴BH=，
∠B=∠ACB=30°，AH⊥BC，则BH=HC=BC，
∴BC=2BH=，
综上所述BC的长为：或或.
【点睛】本题考查了特殊平行四边形的判定和性质，折叠的性质，等腰三角形的判定和性质，含30°直角三角形，勾股定理等知识；正确作出图形并分类讨论是解题关键．