
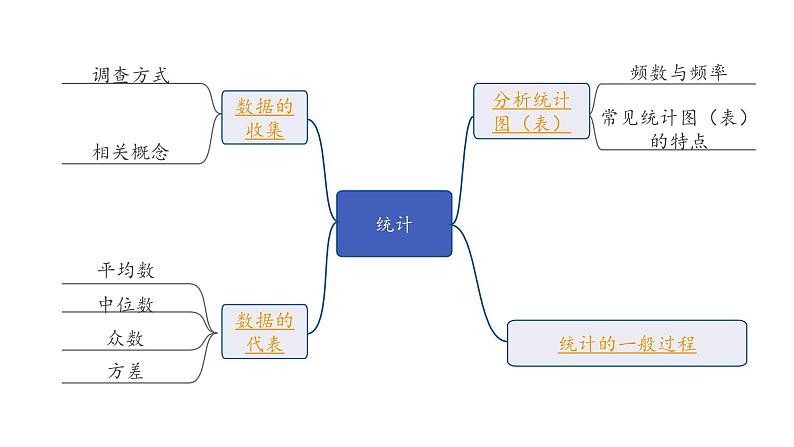




2024河北中考数学一轮中考考点研究 统计(课件)
展开【对接教材】冀教:八下第十八章P1-P25,九上第二十三章P1-P30; 人教:七下第十章P134-P161,八下第二十章P110-P137; 北师:七上第六章P154-P188,八上第六章P135-P160.
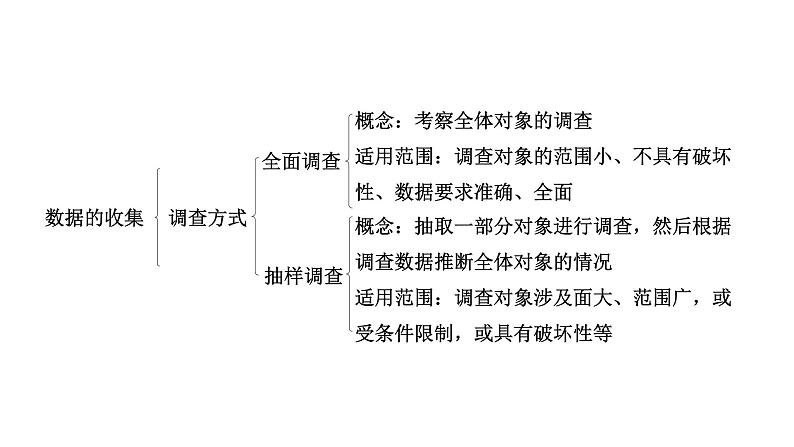
概念:考察全体对象的调查适用范围:调查对象的范围小、不具有破坏性、数据要求准确、全面
概念:抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况适用范围:调查对象涉及面大、范围广,或受条件限制,或具有破坏性等
总体:所要考察对象的______个体:组成总体的每一个对象样本:从总体中抽取的一部分个体样本容量:样本中包括的个体的数目
1. 一般地,如果有n个数x1,x2,…,xn,那么 =__________________
=________________________. 其中f1, f2,…, fk分别表示x1,x2,…,xk出现的次数,n=f1+f2+…+fk
2. 如果有n个数x1,x2,…,xn,都比较接近a,则可让每一个数据都减去a,得到一组新数据x′1,x′2,…,x′n,先求出新数据的平均数x′,则原数据的平均数 ,此方法多用于一组数据较大时
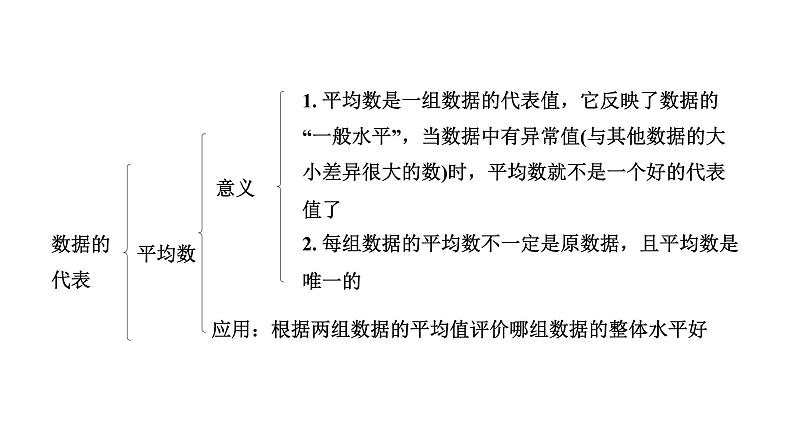
应用:根据两组数据的平均值评价哪组数据的整体水平好
1. 平均数是一组数据的代表值,它反映了数据的“一般水平”,当数据中有异常值(与其他数据的大小差异很大的数)时,平均数就不是一个好的代表值了2. 每组数据的平均数不一定是原数据,且平均数是唯一的
概念:一般地,将n个数据按大小顺序排列,如果n为奇数,那么把处于________的数据叫做这组数据的中位数,如果n为偶数,那么把处于__________________________叫做这组数据的中位数特点:(1)中位数侧重在顺序方面描述一组数据的集中趋势,去掉一组数据中的一个最大值和一个最小值,中位数不变(2)中位数不一定是原数据,且中位数只有一个
当数据中存在极值时,一般选取中位数表示这组数据的集中趋势更能体现数据的集中趋势.
中间位置的两个数据的平均数
应用:判断某个数据在某组数据中的位置时,比中位数大,即位于前50%变化规律:同原数据的变化一致
概念:一般地,把一组数据中出现次数最多的那个数据叫做众数
一组数据的众数可能不止一个,也可能没有,且众数一定是原数据.
特点:表示一组数据中出现次数最多的数据,能够反映一组数据的集中趋势应用:最受欢迎、最满意、最应该关注等都与众数有关变化规律:同原数据的变化一致
计算公式:s2= [(x1- )2+(x2- )2+…+(xn- )2]特点:反映一组数据波动大小(离散程度)的量,方差越大,数据的波动越_____,偏离平均数越大,数据越_______;方差越小,数据的波动越_____,偏离平均数越小,数据越________应用:当几组数据的平均数相同时,用方差来比较几组数据的稳定性
一组数据中所有数值都相等时,方差为0
①增加一个极端值,方差变________,增加一个平均数,方差变________②减少一个极端值,方差变________,减少一个平均数,方差变________③某个数据“靠近”平均数时,方差变_____④某个数据“远离”平均数时,方差变_____⑤某个数据增大或减小对引起方差的变化不能确定
数据变化对平均数、方差的影响
频数:各组中数据的个数
各组频数的和等于这组数据个数的总数,各组数据的频率之和等于1;频数与频率都能反映各组数据出现的频繁程度.
常见统计图(表)的特点
统计的一般过程(2019年11题考查)
例1 某中学为了解学生对于《数学的奥秘》这本书的阅读效果,对全校学生进行阅读效果测试,从初一、初二的学生中随机各选20名学生的成绩,数据如下:
(1)以上这种调查方式为______调查(填“全面”或“抽样”);(2)在这次调查中:总体是_______________________________________ ;个体是_______________________________________ ;样本是__________________________________________________ ;样本容量是_____ ;
全校学生阅读《数学的奥秘》的测试成绩
每个学生阅读《数学的奥秘》的测试成绩
初一、初二各20名学生阅读《数学的奥秘》的测试成绩
(3)整理数据将初一学生得分按分数段整理成不完整的统计表,如下表:
并按照分数段绘制成不完整的频数分布直方图,如图①.
将初二学生得分绘制成不完整的扇形统计图,如图②.
①表中a=__________,b=____________,并补全频数分布直方图;
②扇形统计图中,70≤x<80所对应的圆心角度数为________;③若该校总共有2000名同学,请估计该校学生中测试成绩在90≤x≤100这个分数段的学生人数;
(4)分析数据①初一、初二所收集的20名学生成绩的平均数、中位数、众数、方差如下表,补全下表;
②本次收集的初一20名学生成绩的中位数落在哪个分数段?
②初一学生成绩的中位数为91,落在90≤x≤100这一分数段;
③经过分析哪个年级的学生成绩相对稳定一些?
③初一学生成绩的方差为96.15.初二学生成绩的方差为113.06.∵96.15<113.06,∴初一学生成绩更稳定;
④你认为哪个年级的学生阅读效果更好,请说明理由;
④初一学生阅读效果更好.理由:初一学生的成绩平均数大于初二学生成绩的平均数,初一学生成绩的方差小于初二学生成绩的方差,更稳定,初一学生成绩的众数大于初二学生成绩的众数;
⑤学校为鼓励学生阅读,对各年级排名前30%的学生进行表彰,初一(1)班的小明同学本次阅读测试的成绩为95分,试估计小明是否能获得表彰.
⑤所抽取的20名初一学生成绩中,前30%即前6名学生的成绩分别为100,96,95,95,95,95,根据样本估计总体,小明的成绩排在前30%,可获得表彰.
例2 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,他们投中的次数统计如下表:
(1)这组数据的中位数为________,平均数为________,方差为________;
(2)若增加一名队员定点投篮的投中次数后使得该组数据的平均数不发生变化,则增加的投中次数应为________;
【解法提示】∵原数据的平均数为6,且增加一个数据后,该组数据的平均数不发生变化,∴增加的队员的投中次数为6.
(3)若去掉一个投中次数3,再去掉一个数据后,使得新数据的中位数与原数据相同,则去掉的投中次数可以是________;
【解法提示】∵原数据的中位数为6,且去掉的一个投中次数为3,∴再去掉一个数据后,要使新数据的中位数与原数据的中位数相同,则去掉的数据可以是7或8.
(4)随后又对另外2名队员进行了定点投篮练习,投中次数分别为3和6,得到一组新数据.①则这组新数据的众数为________;②若要使这组新数据没有众数,则至少应去掉______个人的投中次数,投中次数是________.
【解法提示】①由题可知,新数据为3,3,5,5,5,6,6,6,7,7,8,8,则这组新数据的众数为5和6;
②要使该组数据没有众数,则每个数据出现的次数应该相同,∴至少应去掉2个人的投中次数,投中次数分别为5和6.
1. (2019河北11题2分)某同学要统计本校图书馆最受学生欢迎的图书种类.以下是排乱的统计步骤:①从扇形图中分析出最受学生欢迎的种类;②去图书馆收集学生借阅图书的记录;③绘制扇形图来表示各个种类所占的百分比;④整理借阅图书记录并绘制频数分布表.正确统计步骤的顺序是( )A. ②→③→①→④ B. ③→④→①→②C. ①→②→④→③ D. ②→④→③→①
2. (2018河北10题3分)图中的手机截屏内容是某同学完成的作业,他做对的题数是( )A. 2个 B. 3个 C. 4个 D. 5个
3. (2018河北9题3分)为考察甲、乙、丙、丁四种小麦的长势,在同一时期分别从中随机抽取部分麦苗,获得苗高(单位:cm)的平均数与方差为: , ;s2甲=s2丁=3.6,s2乙=s2丙=6.3,则麦苗又高又整齐的是( )A. 甲 B. 乙 C. 丙 D. 丁
4. (2020河北5题3分)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=( )
A. 9 B. 8 C. 7 D. 6
当a=9时,中位数与众数不相等,故不符合题意;
当a=8时,中位数与众数相等,符合题意;
当a=7时,无众数,故不符合题意;
当a=6时,中位数与众数不相等,故不符合题意.
5. (2014河北16题3分)五名学生投篮球,规定每人投20次,统计他们每人投中的次数,得到五个数据.若这五个数据的中位数是6,唯一众数是7,则他们投中次数的总和可能是( )A. 20 B. 28 C. 30 D. 31
6. (2017河北14题2分)甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图.比较5月份两组家庭用水量的中位数,下列说法正确的是( )A. 甲组比乙组大 B. 甲、乙两组相同C. 乙组比甲组大 D. 无法判断
甲组12户家庭用水量统计表
乙组12户家庭用水量统计图
7. (2021河北14题2分)小明调查了本班每位同学最喜欢的颜色,并绘制了不完整的扇形图①及条形图②(柱的高度从高到低排列).条形图不小心被撕了一块,图②中“( )”应填的颜色是( )A. 蓝 B. 粉 C. 黄 D. 红
∴“( )”应填的颜色为红
8. (2012河北21题8分)某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.小宇根据他们的成绩绘制了如下尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
甲、乙两人射箭成绩统计表
(1)a=________,x乙=________;(2)请完成图中表示乙成绩变化情况的折线图;
(2)补全拆线图如解图;
(3)①观察图,可看出________的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断;
②∵两人平均成绩相同,但乙的成绩比甲的成绩稳定,∴乙将被选中.(8分)
②请你从平均数和方差的角度分析,谁将被选中?
9. (2013河北22题10分)某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图①)和条形图(如图②),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:(1)写出条形图中存在的错误,并说明理由;
解:(1)D类型的人数有错.理由:20×10%=2≠3;(2分)
(2)写出这20名学生每人植树量的众数、中位数;
(2)众数为5棵,中位数为5棵;(5分)
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:第一步:求平均数的公式是 ;第二步:在该问题中,n=4,x1=4,x2=5,x3=6,x4=7;第三步: =5.5(棵).①小宇的分析是从哪一步开始出现错误的?
(3)①第二步;(6分)
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
10. (2014河北22题10分)如图①,A,B,C是三个垃圾存放点,点B、C分别位于点A的正北和正东方向,AC=100米.四人分别测得∠C的度数如下表:
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图②,③:
(1)求表中∠C度数的平均数 ;
(2)求A处的垃圾量,并将图②补充完整;
(3)用(1)中的x作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:sin37°≈0.6,cs37°≈0.8,tan37°≈0.75)
(3)∵点B、C分别位于点A的正北和正东方向,∴∠BAC=90°.在Rt△BAC中,∵AC=100米,∠C=37°,∴AB= AC·tan37°≈100×0.75=75(米),∴运垃圾所需的费用是0.005×80×75=30(元).(10分)
11. (2015河北24题11分)某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图:
A,B产品单价变化统计表
A,B产品单价变化折线图
并求得了A产品三次单价的平均数和方差: =5.9;s2A= [(6-5.9)2+(5.2-5.9)2+(6.5-5.9)2]= .(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了________%;
解:(1)补全折线图如解图:A,B产品单价变化折线图(2分)
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
2024河北中考数学一轮中考考点研究 第八章 统计与概率 第二节 概率(课件): 这是一份2024河北中考数学一轮中考考点研究 第八章 统计与概率 第二节 概率(课件),共48页。PPT课件主要包含了确定事件,事件的分类,概率的计算,1随机不可能,5列表如下,6列表如下,8①列表如下,第2题图,第3题图,思路分析等内容,欢迎下载使用。
2024贵阳中考数学一轮贵阳中考考点研究 第32讲 概 率(课件): 这是一份2024贵阳中考数学一轮贵阳中考考点研究 第32讲 概 率(课件),共32页。PPT课件主要包含了m+n=10,考点精讲,事件的分类,确定事件,概率的计算等内容,欢迎下载使用。
2024贵阳中考数学一轮贵阳中考考点研究 第31讲 统 计(课件): 这是一份2024贵阳中考数学一轮贵阳中考考点研究 第31讲 统 计(课件),共44页。PPT课件主要包含了数据的收集与整理,考点精讲,调查方式,抽样调查,适用情况,部分个体,表的分析,频数与频率,数据总数,常见统计图的特点等内容,欢迎下载使用。












