2024贵州中考数学一轮知识点复习 微专题 对称性质在最值中的应用（课件）

这是一份2024贵州中考数学一轮知识点复习 微专题 对称性质在最值中的应用（课件），共19页。PPT课件主要包含了第1题图，第2题图，第3题图，第4题图，第5题图，第6题图，第7题图，第8题图，1－12，第9题图等内容，欢迎下载使用。

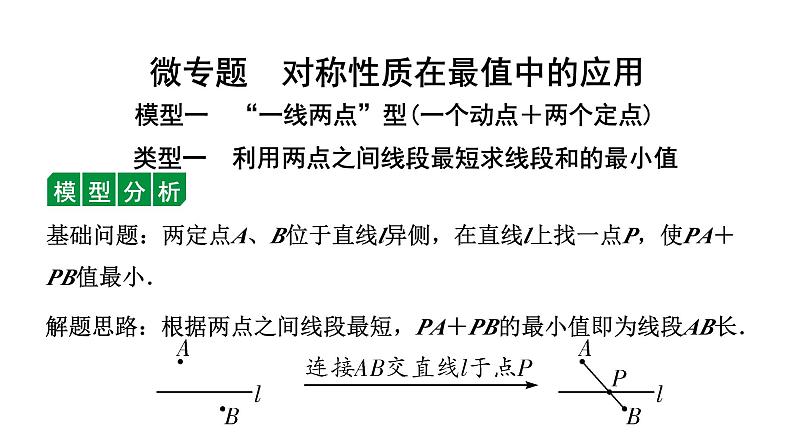
问题：两定点A、B位于直线l同侧，在直线l上找一点P，使得PA＋PB值最小．
解题思路：将两定点同侧转化为异侧问题，同“基础模型”即可解决．
(注：也可以作点A关于直线l的对称点A′，连接A′B，与直线l交于点P′)
1. 如图，在矩形ABCD中，AB＝6，AD＝3，点P为矩形ABCD内一点，且动点P满足S△PAB＝ S矩形ABCD，则点P到A、B两点距离之和的最小值为(　　)A. 2 B. 2C. 3 D.
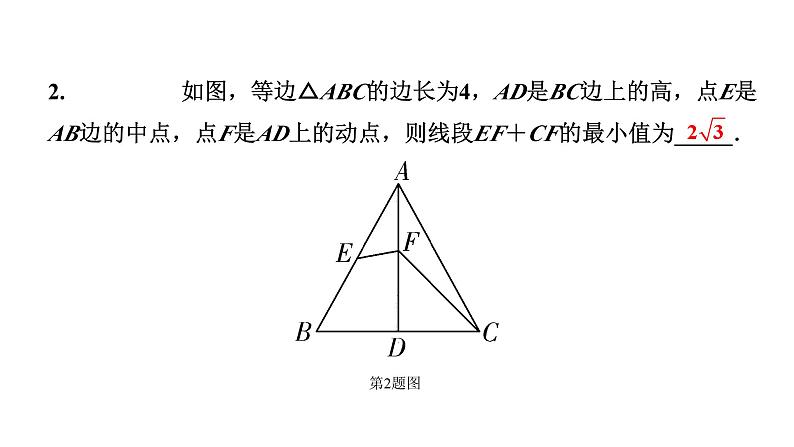
2. 如图，等边△ABC的边长为4，AD是BC边上的高，点E是AB边的中点，点F是AD上的动点，则线段EF＋CF的最小值为_____．
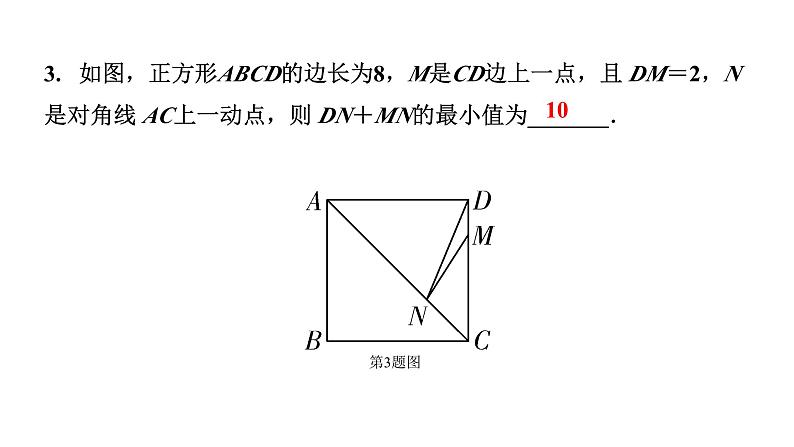
3. 如图，正方形ABCD的边长为8，M是CD边上一点，且 DM＝2，N是对角线 AC上一动点，则 DN＋MN的最小值为_______．
4. 如图，抛物线y＝ax2＋bx＋3(a≠0)与x轴交于A，B两点(点B在点A的右侧)，与y轴交于点C，OB＝OC，抛物线的对称轴为直线x＝1.点P为抛物线的对称轴上一点，当△ACP的周长最小时，点P的坐标为______．
类型二　利用三角形两边之差小于第三边求线段差的最大值
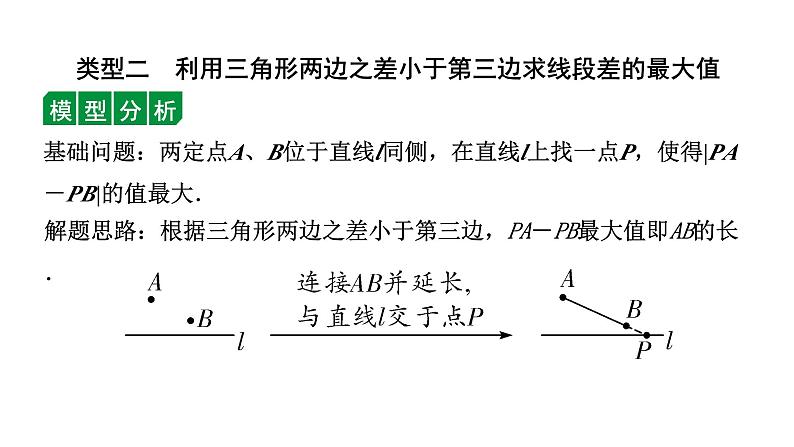
基础问题：两定点A、B位于直线l同侧，在直线l上找一点P，使得|PA－PB|的值最大．
解题思路：根据三角形两边之差小于第三边，PA－PB最大值即AB的长．
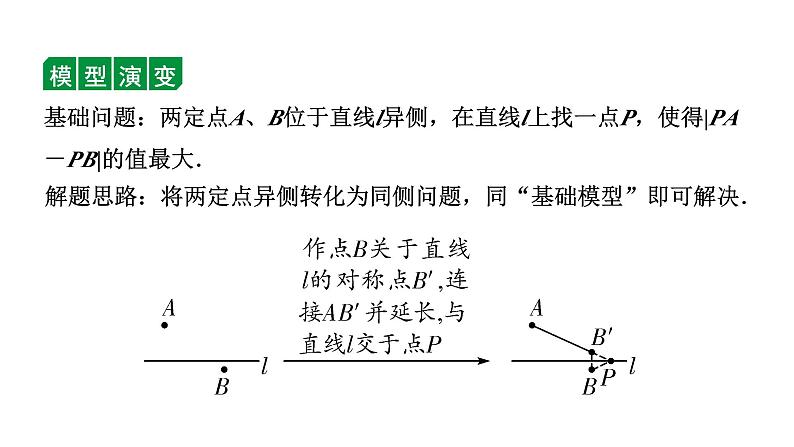
基础问题：两定点A、B位于直线l异侧，在直线l上找一点P，使得|PA－PB|的值最大．
解题思路：将两定点异侧转化为同侧问题，同“基础模型”即可解决．
5. 如图，在Rt△ABC中，AC＝4，BC＝5，EF是BC的垂直平分线，点P是EF上的动点，则|PA－PB|的最大值为________．
6. 如图，在正方形ABCD中，AB＝8，AC与BD交于点O，N是AO的中点，点M在BC边上，且BM＝6.P为对角线BD上一点，则PM－PN的最大值为__________．
7. 如图，已知△ABC为等腰直角三角形，AC＝BC＝4，∠BCD＝15°，P为CD上的动点，则|PA－PB|的最大值为________．
8. 已知抛物线y＝x2－2x－8与x轴交于点A、B(点A在点B的左侧)，与y轴交于点C，P是抛物线对称轴上的一个动点，则当|PB－PC|最大时，点P的坐标为___________．
模型二　“一点两线”型(两个动点＋一个定点)
类型一　利用两点之间线段最短求周长的最小值
基础问题：点P是∠AOB的内部一定点，在OA上找一点M，在OB上找一点N，使得△PMN的周长最小．
解题思路：要使△PMN周长最小，即PM＋MN＋PN值最小，根据两点之间线段最短，将三条线段转化到同一直线上．
9. 如图，在△ABC中，AB＝AC，∠BAC＝90°，点D为AB上一定点，点E、F分别为边AC、BC上的动点，当△DEF的周长最小时，∠FDE的大小为________．
10. 如图，四边形ABCD中，∠A＝60°，∠B＝∠D＝90°，AB＝AD＝ ，点M、N分别是AB、AD上的动点，则△CMN周长的最小值为________．
11. 如图，点P是菱形AOBC内一点，∠C＝45°，OP＝2，点M和点N分别是射线OA，OB上的动点，则△PMN周长的最小值是________．
类型二　利用垂线段最短求线段和的最小值
基础问题：点P是∠AOB的内部或边上一定点，在OA上找一点M，在OB上找一点N，使得PN＋MN的值最小．
解题思路：要使PN＋MN的值最小，可利用对称性，将两条线段转化到同一直线上．
12. 如图，在Rt△ABC中，∠ACB＝90°，AC＝6, BC＝8，AD是∠BAC的平分线．若P、Q分别是AD、AC上的动点，则PC＋PQ的最小值是________．