2023-2024学年北京市首都师大附中高一（下）期中数学试卷（含答案）

这是一份2023-2024学年北京市首都师大附中高一（下）期中数学试卷（含答案），共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1.下列函数中，既是偶函数又是周期为π的函数为( )
A. y=sinxB. y=csxC. y=tan2xD. y=cs2x
2.若α是第二象限的角，P(x,6)为其终边上的一点，且sinα=35，则x=( )
A. −4B. ±4C. −8D. ±8
3.角的度量除了有角度制和弧度制之外，在军事上角的度量还有密位制，密位制的单位是密位.1密位等于圆周角的16000，即2π弧度=360°=6000密位.在密位制中，采用四个数字来记一个角的密位数.且在百位数字与十位数字之间画一条短线，例如3密位写成0−03，123密位写成1−23，设圆的半径为1，那么10−00密位的圆心角所对的弧长为( )
A. π6B. π4C. π3D. π2
4.已知A(1,2)，B(3,7)，a=(x,−1)，AB//a，则( )
A. x=25，且AB与a方向相同B. x=−25，且AB与a方向相同
C. x=25，且AB与a方向相反D. x=−25，且AB与a方向相反
5.关于函数y=3cs(2x+π3)，则下列结论中：
①−π为该函数的一个周期；
②该函数的图象关于直线x=π3对称；
③将该函数的图象向左平移π6个单位长度得到y=3cs2x的图象；
④该函数在区间[−π6,π6]上单调递减．
所有正确结论的序号是( )
A. ①②B. ③④C. ①②④D. ①③④
6.设a，b是两个不共线向量，则“a与b的夹角为钝角”是“a⊥(a+b)”的( )
A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
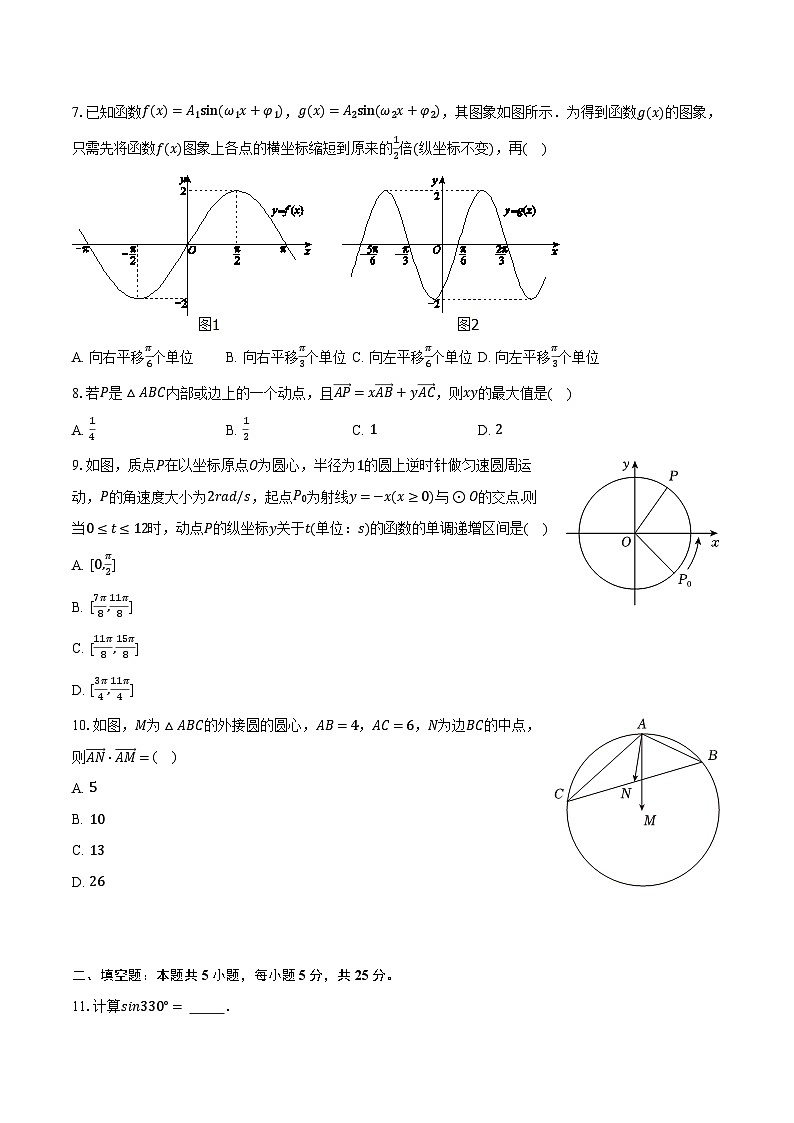
7.已知函数f(x)=A1sin(ω1x+φ1)，g(x)=A2sin(ω2x+φ2)，其图象如图所示．为得到函数g(x)的图象，只需先将函数f(x)图象上各点的横坐标缩短到原来的12倍(纵坐标不变)，再( )
A. 向右平移π6个单位B. 向右平移π3个单位C. 向左平移π6个单位D. 向左平移π3个单位
8.若P是△ABC内部或边上的一个动点，且AP=xAB+yAC，则xy的最大值是( )
A. 14B. 12C. 1D. 2
9.如图，质点P在以坐标原点O为圆心，半径为1的圆上逆时针做匀速圆周运动，P的角速度大小为2rad/s，起点P0为射线y=−x(x≥0)与⊙O的交点.则当0≤t≤12时，动点P的纵坐标y关于t(单位：s)的函数的单调递增区间是( )
A. [0,π2]
B. [7π8,11π8]
C. [11π8,15π8]
D. [3π4,11π4]
10.如图，M为△ABC的外接圆的圆心，AB=4，AC=6，N为边BC的中点，则AN⋅AM=( )
A. 5
B. 10
C. 13
D. 26
二、填空题：本题共5小题，每小题5分，共25分。
11.计算sin330°= ．
12.已知α是第四象限角，且tanα=−512，则csα= ______，cs(π2+α)= ______．
13.a,b在正方形网格中的位置如图所示，则〈a,b〉= ______，向量a在向量b上的投影的数量为______．
14.已知函数f(x)=cs(2x+φ)(|φ|<π2)的图象关于直线x=11π10对称，且f(x)在[π6,m]上单调，则m的最大值为______．
15.已知函数f(x)=sinπxx2−x，给出下列四个结论：
①f(x)存在无数个零点；
②f(x)在(1,+∞)上有最大值；
③若f(2023.7)=a，则f(−2022.7)=a；
④区间(12,1)是f(x)的单调递减区间．
其中所有正确结论的序号为______．
三、解答题：本题共5小题，共55分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题11分)
如图，在平行四边形ABCD中，AE=2AB，DF=13DE.设AB=a，AD=b．
(Ⅰ)用a，b表示AC，DE；
(Ⅱ)用向量的方法证明：A，F，C三点共线．
17.(本小题11分)
已知函数f(x)=sin(2x−φ)，其中|φ|<π2，且y=f(x)的图象过点(π12,0)．
(Ⅰ)求φ的值；
(Ⅱ)求f(x)的单调减区间和对称中心的坐标；
(Ⅲ)若m>0，函数f(x)在区间[0,m]上最小值为−12，求实数m的取值范围．
18.(本小题11分)
在平面直角坐标系xOy中，已知点A(3,3)，B(5,1)，P(2,1)，点M是直线OP上的一个动点．
(Ⅰ)求|PA−PB|的值；
(Ⅱ)若四边形APBQ是平行四边形，求点Q的坐标；
(Ⅲ)求MA⋅MB的最小值．
19.(本小题11分)
在条件①对任意的x∈R，都有f(π6−x)=f(x)；条件②f(x)最小正周期为π；条件③f(x)在[−5π12,π12]上为增函数，这三个条件中选择两个，补充在下面的题目中，并解答．
已知f(x)=sin(ωx+φ)，(ω>0,0≤φ<2π)，若_____，则ω，φ唯一确定．
(Ⅰ)求f(x)的解析式；
(Ⅱ)设函数g(x)=2f(x+π6)+1，对任意的x∈[−π6,π12]，不等式g2(x)−mg(x)−1≤0恒成立，求实数m的取值范围．
20.(本小题11分)
设Sn={(x1,x2,…,xn)|xi∈{0，1}，i=1，2，…，n}(n为正整数)，对任意的α=(x1,x2,…,xn)，β=(y1,y2,…,yn)，定义α⋅β=x1y1+x2y2+…+xnyn．
(Ⅰ)当n=3时，α=(1,1,0)，β=(1,0,1)，求α⋅β；
(Ⅱ)当n=3时，集合A⊆Sn，对于任意α，β∈A，α⋅β圴为偶数，求A中元素个数的最大值；
(Ⅲ)集合A⊆Sn，对于任意α，β∈A，α≠β，均有α⋅β≠0，求A中元素个数的最大值．
答案和解析
1.【答案】D
【解析】解：对于A，函数y=sinx为奇函数，周期为2π，故A错误；
对于B，函数y=csx为偶函数，周期为2π，故B错误；
对于C，函数y=tan2x为奇函数，周期为12π，故C错误；
对于D，函数y=cs2x为偶函数，周期为2π2=π，故D正确．
故选：D．
根据三角函数的奇偶性和周期公式，逐个判断各个选项即可．
本题主要考查了三角函数的奇偶性和周期性，属于基础题．
2.【答案】C
【解析】【分析】
由题意与三角函数的定义可得：6 x2+62=35，x<0，解出即可得出．
本题考查了三角函数的定义，考查了推理能力与计算能力，属于基础题．
【解答】
解：∵α是第二象限的角，P(x,6)为其终边上的一点，且sinα=35，
∴6 x2+62=35，x<0，
解得x=−8．
故选C．
3.【答案】C
【解析】解：由题意知10−00密位的圆心角为10006000×2π=π3，
所以弧长为π3×1=π3．
故选：C．
运用密位制与弧度制公式及弧长公式计算即可．
本题考查了密位制与弧度制公式及弧长公式的应用，属于基础题．
4.【答案】D
【解析】【分析】
本题考查向量共线的坐标表示，向量的坐标运算，是基础题．
求出AB向量，利用向量平行求出x，然后判断两个向量的方向关系即可．
【解答】
解：A(1,2)，B(3,7)，可得AB=(2,5)，
a=(x,−1)，AB//a，
可得5x=−2，解得x=−25．
a=(−25,−1)，与AB方向相反．
故选：D．
5.【答案】C
【解析】解：设f(x)=3cs(2x+π3)，
∵f(x−π)=3cs[2(x−π)+π3]=3cs(2x−2π+π3)=3cs(2x+π3)=f(x)，∴−π为该函数的一个周期，①正确；
∵f(2π3−x)=3cs[2(2π3−x)+π3]=3cs(5π3−2x)=3cs[2π−(2x+π3)]=3cs(2x+π3)=f(x)，∴该函数的图象关于直线x=π3对称，②正确；
将该函数的图象向左平移π6个单位长度得到f(x+π6)=3cs[2(x+π6)+π3]=3cs(2x+2π3)≠y=3cs2x，③错误；
∵x∈[−π6,π6]，∴2x+π3∈[0,2π3]，而y=csx在[0,π]上单调递减，所以④正确．
故选：C．
根据余弦函数的周期性，对称性，单调性以及图象的变换分别判断即可．
本题考查余弦函数的性质，属于中档题．
6.【答案】B
【解析】解：由于a，b是两个不共线向量，则“a与b的夹角为钝角”
所以a⋅b=|a||b|csθ<0；且a⋅b≠−|a||b|，即θ≠π；
由于a⊥(a+b)，
所以a2+a⋅b=0，整理得a⋅b=−a2<0，
故“a与b的夹角为钝角”是“a⊥(a+b)”的必要不充分条件．
故选：B．
直接利用向量的线性运算，向量的数量积，充分条件和必要条件的应用判断出结果．
本题考查的知识要点：向量的线性运算，向量的数量积，充分条件和必要条件，主要考查学生的运算能力和数学思维能力，属于基础题．
7.【答案】A
【解析】解：函数f(x)=A1sin(ω1x+φ1)，g(x)=A2sin(ω2x+φ2)，其图象如图所示，
可见f(x)的周期为2π，g(x)的周期为π，且f(x)图象上的点(0,0)，在g(x)的图象上对应(π6,0)，
为得到函数g(x)的图象，只需先将函数f(x)图象上各点的横坐标缩短到原来的12倍(纵坐标不变)，
在向右平移π6个单位，
故选：A．
利用函数y=Asin(ωx+φ)的图象变换规律，得出结论．
本题主要考查函数y=Asin(ωx+φ)的图象变换规律，属于基础题．
8.【答案】A
【解析】解：因为P是△ABC内部或边上的一个动点且AP=xAB+yAC，
当P在BC上时，x+y=1，
特别地，当P与B重合时，x=1，y=0，当P与C重合时，x=0，y=1，
故0则xy≤(x+y2)2=14，当且仅当x=y=12时取等号，
此时xy取最大值14．
故选：A．
由已知结合平面向量基本定理及基本不等式即可求解．
本题主要考查了平面向量基本定理及基本不等式在最值求解中的应用，属于基础题．
9.【答案】B
【解析】解：因为P在单位圆上的角速度大小为2rad/s，起点P0为射线y=−x(x≥0)与⊙O的交点，
所以A=1，ω=2,φ=−π4，所以动点P的纵坐标y关于t(单位：S)的函数y=sin(2t−π4)，
由−π2+2kπ≤2t−π4≤π2+2kπ,k∈Z，得−π8+kπ≤t≤3π8+kπ，k∈Z，
因为0≤t≤12，所以0≤t≤3π8，7π8≤t≤11π8，15π8≤t≤19π8，23π8≤t≤27π8．
所以动点P的纵坐标y关于t(单位：S)的函数的单调递增区间是：
[0,3π8]，[7π8,11π8]，[15π8,19π8]，[23π8,27π8]．
故选：B．
根据题意求出y关于t(单位：S)的函数y=sin(2t−π4)，然后结合正弦函数的单调性求解函数在[0,12]上的增区间．
本题考查三角函数定义，考查三角函数性质，属于中档题．
10.【答案】C
【解析】【分析】
本题考查了向量的平行四边形法则、三角形外接圆的性质、数量积运算定义，考查了推理能力与计算能力，属于中档题．
由N是BC边的中点，可得AN=12(AB+AC)，利用M是△ABC的外接圆的圆心，可得AM⋅AB=|AM||AB|cs∠BAM=12|AB|2=12×42=8，同理可得AM⋅AC=12|AC|2=18，即可得出结论．
【解答】
解：∵N是BC边的中点，可得AN=12(AB+AC)，
∵M是△ABC的外接圆的圆心，
∴AM⋅AB=|AM||AB|cs∠BAM=12|AB|2=12×42=8，
同理可得AM⋅AC=12|AC|2=18，
∴AN⋅AM=12(AB+AC)⋅AM=12AM⋅AB+12AM⋅AC=12×8+12×18=13．
故选C．
11.【答案】−12
【解析】【分析】
此题考查了诱导公式的作用，熟练掌握诱导公式是解本题的关键，属于基础题．
所求式子中的角变形后，利用诱导公式化简即可得到结果．
【解答】
解：sin330°=sin(360°−30°)=−sin30°=−12．
故答案为−12．
12.【答案】1213 513
【解析】解：因为α是第四象限角，且tanα=−512，
则csα= 11+tan2α=1213，sinα=− 1−cs2α=−513，
故cs(π2+α)=−sinα=513．
故答案为：1213；513．
由已知结合同角基本关系及诱导公式进行化简即可求解．
本题主要考查了同角基本关系及诱导公式的应用，属于基础题．
13.【答案】3π4 − 5
【解析】解：由题意可知：a=(3,1)，b=(−1,−2)，
则a⋅b=3×(−1)+1×(−2)=−5，
又|a|= 10，|b|= 5，
则cs=a⋅b|a||b|=−5 10× 5=− 22，
又∈[0,π]，
则〈a,b〉=3π4；
向量a在向量b上的投影的数量为|a|cs= 10×(− 22)=− 5．
故答案为：3π4；− 5．
由平面向量数量积的坐标运算，结合平面向量夹角的运算求解．
本题考查了平面向量数量积的坐标运算，属基础题．
14.【答案】3π5
【解析】解：∵函数f(x)=cs(2x+φ)(|φ|<π2)的图象关于直线x=11π10对称，
∴2×11π10+φ=kπ，k∈Z，∴φ=−π5，函数f(x)=cs(2x−π5).
∵f(x)在[π6,m]上单调，2x−π5∈[2π15,2m−π5].
∴2m−π5≤π，∴m≤3π5，故m的最大值为3π5，
故答案为：3π5．
由题意，利用余弦函数的单调性以及它的图象的对称性，求得m的最大值．
本题主要考查余弦函数的单调性以及它的图象的对称性，属于中档题．
15.【答案】①②③
【解析】解：对于①，由x2−x≠0，可得x≠0且x≠1，即函数f(x)的定义域为(−∞,0)∪(0,1)∪(1,+∞)，
令f(x)=0可得sinπx=0，则πx=kπ(k∈Z)，且x∈(−∞,0)∪(0,1)∪(1,+∞)，
故x=k(k∈Z,k≠0,k≠1)，所以函数f(x)有无数个零点，①对；
对于②，当x>1时，x2−x=x(x−1)>0，
令sinπx≥0，可得2kπ≤πx≤(2k+1)π(k∈N*)，解得2k≤x≤2k+1(k∈N*)，
假设函数f(x)在(1,+∞)上的最大值点为x0，则x0∈[2k,2k+1](k∈N*)，
因为函数y=x2−x2在(1,+∞)上单调递增，且y=x2−x>0，
对任意的x∈[2k,2k+1](k∈N*)，且t∈N*，则(x+2t)2−(x+2t)>x2−x>0，
所以1x2−x>1(x+2t)2−(x+2t)>0，
则f(x+2t)=sin(πx+2tπ)(x+2t)2−(x+2t)=sinπx(x+2t)2−(x+2t)≤sinπxx2−x=f(x)，
所以若f(x)在(1,+∞)上存在最大值点x0，则x0∈[2,3]，
因为函数f(x)在[2,3]上是一条连续不断的曲线，所以函数f(x)在[2,3]上存在最大值，
故函数f(x)在(1,+∞)上存在最大值，②对；
对于③，对任意的x∈(−∞,0)∪(0,1)∪(1,+∞)，
f(1−x)=sin(π−πx)(1−x)2−(1−x)=sinπxx2−x=f(x)，
因为2023.7−2022.7=1，所以若f(2023.7)=a，则f(−2022.7)=a，③对；
对于④，f(23)=sin2π3(23)2−23= 32×(−92)=−9 34，
f(34)=sin34π(34)2−34= 22×(−163)=−8 23，
因为(9 34)2−(8 23)2=24316−1289=2187−204848>0，即9 34>8 23，故f(23)故函数f(x)在(12,1)上不可能单调递减，④错．
故答案为：①②③．
解方程f(x)=0，可判断①；分析出函数f(x)在(1,+∞)的最大值点在区间[2,3]内，再利用最值定理可判断②；推导出f(1−x)=f(x)，可判断③；利用特殊值法可判断④．
本题主要考查函数的单调性与最值，考查运算求解能力与逻辑推理能力，属于中档题．
16.【答案】(Ⅰ)解：平行四边形ABCD中，AC=AB+AD=a+b，
由于AE=2AB，AB=a，则AE=2a，又AD=b，则在△ADE中，有DE=2a−b，
(Ⅱ)证明：∵DF=13DE.∴DF=13(2a−b)，
在△DFC中，CF=CD+DF=−a+13(2a−b)=−13(a+b)=−13AC，
即FC=13AC，又CF与AC有公共点C，则A，F，C三点共线．
【解析】本题考查向量的线性表示，考查平行四边形法则和三角形法则，属于基础题．
(Ⅰ)分别利用平行四边形法则和三角形法则可表示所求向量；
(Ⅱ)在△DFC中，把表示出来，可发现FC与AC的线性关系，从而证明三点共线．
17.【答案】解：(Ⅰ)根据题意得f(π12)=sin(π6−φ)=0，结合|φ|<π2，可得φ=π6；
(Ⅱ)由(Ⅰ)的结论，得f(x)=sin(2x−π6)，
令2kπ+π2≤2x−π6≤2kπ+3π2，k∈Z，解得kπ+π3≤x≤kπ+5π6，k∈Z，
所以f(x)的单调减区间为[kπ+π3,kπ+5π6]，k∈Z，
由2x−π6=kπ，k∈Z，得x=kπ2+π12，可得f(x)图象的对称中心的坐标为(kπ2+π12,0)，k∈Z；
(Ⅲ)当0≤x≤m时，−π6≤2x−π6≤2m−π6，
因为f(0)=−12，且f(x)在区间[0,m]上的最小值为−12，
所以f(m)≥−12且m【解析】(Ⅰ)根据f(π12)=0列式得到关于φ的等式，结合|φ|<π2求出φ的值；
(Ⅱ)由(Ⅰ)可得f(x)=sin(2x−π6)，从而根据正弦函数的单调区间公式与正弦曲线的对称中心坐标公式，算出所求答案；
(Ⅲ)根据题意，f(0)=−12恰好是最小值，因此可得f(m)≥−12且区间[0,m]的长度小于一个周期，由此建立关于m的不等式，解出实数m的取值范围．
本题主要考查三角函数的解析式求法、正弦函数的图象与性质、函数的单调性与最值等知识，考查了计算能力，属于中档题．
18.【答案】解：(Ⅰ)∵点A(3,3)，B(5,1)，P(2,1)，
∴PB=(3,0)，PA=(1,2)，
∴PB−PA=(2,−2)，
∴|PA−PB|=|PB−PA|= 22+(−2)2=2 2．
(Ⅱ)设点Q(x,y)．
∵四边形APBQ是平行四边形，
∴PA=BQ，
∴(1,2)=(x−5,y−1)，
∴x−5=1y−1=2，
解得x=6y=3．
∴Q(6,3)．
(Ⅲ)设点M(x,y)．
则OM=(x,y)．
由题意OM//OP．
∴x−2y=0，
即x=2y．
∴M(2y,y)．
∴MA⋅MB=(3−2y,3−y)⋅(5−2y,1−y)
=5y2−20y+18
=5(y−2)2−2，
∴当y=2时，MA⋅MB取得最小值−2，此时M(4,2)．
【解析】(Ⅰ)利用向量的坐标运算和模的计算公式即可得出；
(Ⅱ)利用平行四边形的性质、向量共线的性质及其坐标坐标运算即可得出；
(Ⅲ)利用向量共线和二次函数的单调性即可得出．
熟练掌握向量的坐标运算和模的计算公式、平行四边形的性质、向量共线的性质、向量共线定理和二次函数的单调性是解题的关键，属中档题．
19.【答案】(Ⅰ)解：若选择①②：由函数f(x)最小正周期为π，得ω=2，即f(x)=sin(2x+φ)，
又由对任意的x∈R，都有f(π6−x)=f(x)，可得f(x)关于x=π12对称，
即2×π12+φ=π2+2kπ，k∈Z，则φ=π3+2kπ，k∈Z，
因为0≤φ<2π，可得φ=π3，所以f(x)=sin(2x+π3)；
若选择②③：由函数f(x)最小正周期为π，可得ω=2，即f(x)=sin(2x+φ)，
又由x∈[−5π12,π12]，可得2x+φ∈[−5π6+φ,π6+φ]，
因为函数f(x)在[−5π12,π12]为单调递增函数，
则φ−5π6≥−π2φ+π6≤π2，
解得，φ=π3，f(x)=sin(2x+π3)；
若选择①③：由对任意的x∈R，都有f(π6−x)=f(x)，可得f(x)关于x=π12对称，
即ω×π12+φ=π2+2kπ，k∈Z，
即φ=π2−ωπ12+2kπ，k∈Z，
又由函数f(x)在[−5π12,π12]为单调递增函数，可得πω≥π12+5π12=π2，
解得0<ω≤2，
又由x∈[−5π12,π12]，可得ωx+φ∈[−5ωπ12+φ,ωπ12+φ]，
因为函数f(x)在[−5π12,π12]为增函数，
则满足−5ωπ12+φ≥2kπ−π2ωπ12+φ≤2kπ+π2，k∈Z，
解得5ωπ12−π2+2kπ≤φ≤π2−ωπ12+2kπ，k∈Z，
所以5ωπ12−π2≤π2−ωπ12≤π2−ωπ12，
即ωπ2≤π，因为0<ω≤2，所以ω=2，
此时φ=π3，f(x)=sin(2x+π3)；
(Ⅱ)由g(x)=2f(x+π6)+1=2sin(2x+π3+π3)+1=2sin(2x+2π3)+1，
因为x∈[−π6,π12]，可得2x+π3∈[π3,5π6]，
所以sin(2x+π3)∈[12,1]，即g(x)∈[2,3]，
又由对任意x∈[−π6,π12]，不等式g2(x)−mg(x)−1≤0恒成立，
即不等式mg(x)≥g2(x)−1恒成立，
即m≥g2(x)−1g(x)恒成立，
令t=g(x)∈[2,3]，
即m≥t2−1t=t−1t恒成立，
令h(t)=t−1t在t∈[2,3]上为单调递增函数，
则h(t)max=h(3)=83，
所以m≥83，即实数m的取值范围为[83,+∞)．
【解析】(I)解：若选择①②、②③和①③，结合三角函数的图象与性质，求得ω，φ的值，即可求得函数f(x)的解析式；
(Ⅱ)由g(x)=2sin(2x+2π3)+1，x∈[−π6,π12]，求得g(x)∈[2,3]，根据题意，转化为m≥g2(x)−1g(x)恒成立，令t=g(x)∈[2,3]，h(t)=t−1t为单调递增函数，求得h(t)max，即可求解．
本题主要考查了函数性质在函数解析式求解中的应用，还考查了由不等式恒成立求解参数范围，体现了转化思想的应用，属于中档题．
20.【答案】解：(Ⅰ)α⋅β=x1y1+x2y2+x3y3=1×1+1×0+0×1=1．
(Ⅱ)α⋅β=x1y1+x2y2+x3y3为偶数，即为0或2，
若α⋅β=0，则A中的任意两个元素相同位置不能同时出现1，
即(0,0,0)，(1,0,0)，(0,1,0)，(0,0,1)共有四个元素，
若 α⋅β=2，则A中必有两组相同位置的元素同为1，
即(0,1,1)，(1,1,1)，元素较少，
所以A中元素个数的最大值为4．
(Ⅲ)因为α=(x1,x2,…,xn)，
α中的“1”变为“0”，“0”变为“1”，
得到λ=(1−x1,1−x2,…,1−xn)，
可知α⋅λ=0，
因为 α⋅β≠0，
α⊂β，则λ⊄β，
因为Sn中有2n个元素，α和λ成对出现在Sn中，现只出现一个，
则A中最多有 2n−1个元素．
【解析】(Ⅰ)根据公式直接计算即可．
(Ⅱ)讨论α⋅β=0和 α⋅β=2时的情况，求解A中元素个数的最大值即可．
(Ⅲ)由所给条件，分析α和λ的关系，进而求解A中元素个数的最大值即可．
本题考查了集合中元素最值的相关知识，属于中档题．