2024成都中考数学第一轮专题复习之第四章 微专题 手拉手模型解决全等、相似问题 练习课件

这是一份2024成都中考数学第一轮专题复习之第四章 微专题 手拉手模型解决全等、相似问题 练习课件，共13页。PPT课件主要包含了第1题图，第2题图等内容，欢迎下载使用。

1. 在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，以AB，AC为一边向Rt△ABC的外侧作等边△ABE，等边△ACD.(1)如图①，连接BD，CE.(ⅰ)求证：△ABD≌△AEC；
(1)(i)证明：∵△ABE为等边三角形，∴AB＝AE，∠EAB＝60°.∵△ACD为等边三角形，∴AD＝AC，∠DAC ＝ 60°，∴∠EAC＝∠DAB.
在△ABD和△AEC中，∴△ABD≌△AEC(SAS)；
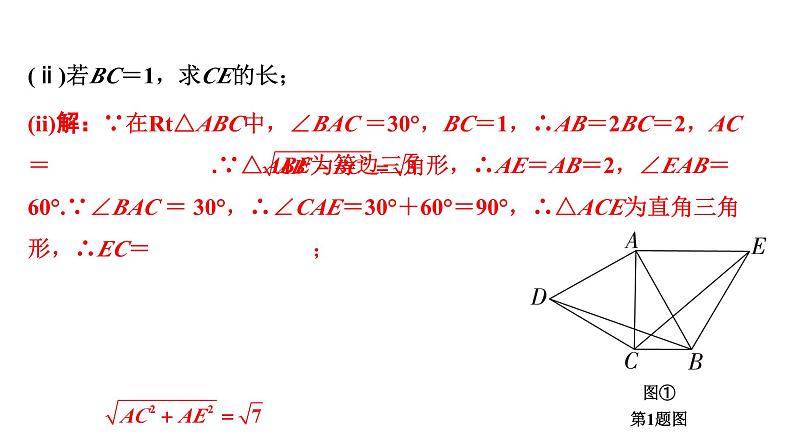
(ⅱ)若BC＝1，求CE的长；
(ii)解：∵在Rt△ABC中，∠BAC ＝30°，BC＝1，∴AB＝2BC＝2，AC＝ .∵△ABE为等边三角形，∴AE＝AB＝2，∠EAB＝60°.∵∠BAC ＝ 30°，∴∠CAE＝30°＋60°＝90°，∴△ACE为直角三角形，∴EC＝ ；
(2)如图②，连接DE交AB于点F.求 的值．
(2)证明：如图，过点E作EG⊥AB于点G.
∵AE＝BE，∴AG＝ AB.∵BC＝ AB，∴AG＝BC.在Rt△AEG与Rt△BAC中，∴Rt△AEG≌Rt△BAC(HL)，∴EG＝AC＝AD.又∵∠EGF＝∠DAF＝90°，
∴在△GFE与△AFD中，∴△GFE≌△AFD(AAS)，∴GF＝AF，∴BG＝AG＝2AF，∴BF＝3AF，∴ ＝3.
2. (2023黄冈)[问题呈现]△CAB和△CDE都是直角三角形，∠ACB＝∠DCE＝90°，CB＝mCA，CE＝mCD，连接AD，BE，探究AD，BE的位置关系．【问题探究】(1)如图①，当m＝1时，直接写出AD，BE的位置关系：________．
【解法提示】如图，延长BE交AD于点G，
∵m＝1，∴AC＝BC，DC＝EC.∵∠DCE＝∠ACB＝90°，∴∠DCA＋∠ACE＝∠ACE＋∠ECB＝90°，∴∠DCA＝∠ECB，∴△DCA≌△ECB，
∴∠DAC＝∠CBE.∵∠CAB＋∠ABG＋∠CBE＝90°，∴∠CAB＋∠ABG＋∠DAC＝90°，即∠AGB＝90°，∴AD⊥BE.
解：(1)AD⊥BE；
(2)如图②，当m≠1时，(1)中的结论是否成立？若成立，给出证明；若不成立，说明理由．
(2)(1)中结论成立．证明：如图，延长BE交AD于点G，
∵∠ACB＝∠DCE＝90°，∴∠ACB－∠ACE＝∠DCE－∠ACE，∴∠ACD＝∠BCE.∵CB＝mCA，CE＝mCD，∴ ，
∴△DCA∽△ECB，∴∠DAC＝∠CBE.∵∠CAB＋∠ABG＋∠CBE＝90°，∴∠CAB＋∠ABG＋∠DAC＝90°，即∠AGB＝90°，∴AD⊥BE.
【拓展应用】(3)当m＝ ，AB＝4 ，DE＝4时，将△CDE绕点C转，使A，D，E三点恰好在同一直线上，求BE的长．