2024成都中考数学第一轮专题复习 图形形状变化问题 教学课件

这是一份2024成都中考数学第一轮专题复习 图形形状变化问题 教学课件，共30页。PPT课件主要包含了第1题图，第1题图②，第2题图，第3题图，第4题图，解题关键点等内容，欢迎下载使用。

类型四　图形形状变化问题(2017.27 )
1. 综合与实践【问题情境】在平行四边形ABCD中，E，H，F，G分别为AB，BC，CD，DA边上的点，线段GH与EF交于点O.【独立思考】(1)如图①，∠A＝90°，GH⊥EF，AB＝5，AD＝k.①用k表示 的值；
(1)①解：如图，过点H作AD的垂线，垂足为M，过点F作AB的垂线，垂足为N.
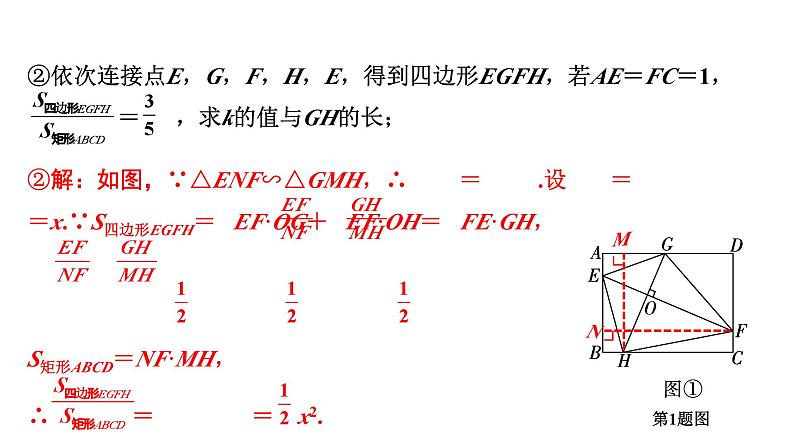
②依次连接点E，G，F，H，E，得到四边形EGFH，若AE＝FC＝1， ＝ ，求k的值与GH的长；
∵ ＝ ，∴ x2＝ ，解得x＝ (负值已舍去)，∴ ＝ ＝ .∵MH＝AB＝5，∴GH＝5× ＝ ，∴EF＝ NF.∵AB＝5，AE＝CF＝1，∴EN＝AB－AE－BN＝3.
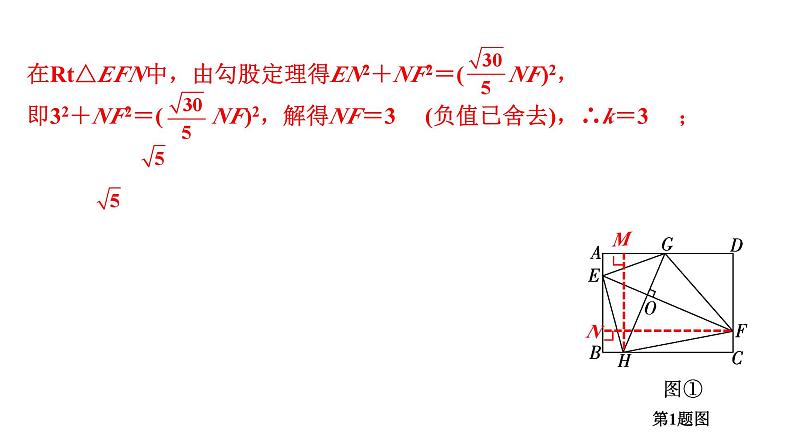
在Rt△EFN中，由勾股定理得EN2＋NF2＝( NF)2，即32＋NF2＝( NF)2，解得NF＝3 (负值已舍去)，∴k＝3 ；
【拓展探究】(2)如图②，连接AO，若∠BAD>90°，∠GOE<90°，且 ＝ ，OE＝OG，求证：∠BAO＝∠DAO.
(2)证明：如图，过点B，E作CD的垂线，分别交DC的延长线于点B′，E′，过点A，G作BC的垂线，垂足分别为A′，G′，EE′与GG′交于点P.
∵AB∥DC，∴∠ABA′＝∠BCB′.∵∠AA′B＝∠BB′C＝90°，∴△ABA′∽△BCB′，∴ ＝ ，∴ ＝ .∵ ＝ ，AD＝BC，∴ ＝ ，∴ ＝ ，∴Rt△GG′H∽Rt△EE′F，∴∠G′GH＝∠E′EF.
∵∠PEO＋∠GPE＝∠EOG＋∠OGP，∴∠EPG＝∠GOE.在四边形AEPG中，∠PEA＝∠AGP＝90°，∴∠EPG＋∠EAG＝180°，∴∠GOE＋∠EAG＝180°，∴A，E，O，G四点共圆．∵EO＝GO，∴∠EAO＝∠DAO.
2. 【问题解决】如图①，在菱形ABCD中，点P为射线AC上的一点，连接DP，过点P作PM，使得∠DPM＋∠BAD＝180°，PM与射线BC交于点M，以PD，PM为邻边作平行四边形DPMN.(1)求证：四边形DPMN为菱形；
(1)证明：如图，过点P作PE⊥CD于点E，PF⊥BC于点F，
∴∠PED＝∠PFM＝∠PEC＝90°，∴∠EPF＋∠BCD＝180°.∵四边形ABCD是菱形，∴∠DCA＝∠BCA，∠BAD＝∠BCD，∴PE＝PF，∠EPF＋∠BAD＝180°.∵∠DPM＋∠BAD＝180°，∴∠DPM＝∠EPF，∴∠DPE＝∠MPF.
在△DPE和△MPF中， ∴△DPE≌△MPF(ASA)，∴PD＝PM.∵四边形DPMN是平行四边形，∴四边形DPMN是菱形；
(2)如图②，当∠BAD＝90°时，连接CN，猜想CN与AP之间的数量关系，并说明理由；
(2)解：AP＝CN.理由如下：∵四边形ABCD和四边形DPMN都是菱形，∠DPM＝∠BAD＝90°，∴四边形ABCD和四边形DPMN都是正方形，∴AD＝CD，DP＝DN，∠ADC＝∠PDN＝90°，∴∠ADP＝∠CDN，∴△ADP≌△CDN(SAS)，∴AP＝CN；
【类比迁移】(3)在(2)的条件下，如图③，当点P在AC的延长线上时，且AB＝3，CP＝ ，求PN的长．
(3)解：由(2)知四边形ABCD和四边形DPMN是正方形，∴AD＝CD，DP＝DN，∠ADC＝∠PDN＝90°，∠DAP＝∠DCA＝45°，∴∠ADC＋∠CDP＝∠PDN＋∠CDP，即∠ADP＝∠CDN，∴△ADP≌△CDN(SAS)，
∴AP＝CN，∠DCN＝∠DAP＝45°，∴∠ACN＝∠DCA＋∠DCN＝90°，∴∠NCP＝90°，在Rt△ADC中，AD＝DC＝AB＝3，∴AC＝3 ，∴CN＝AP＝AC＋CP＝3 ＋ ＝4 ，∴在Rt△PCN中，PN＝ ＝ .
3. (2017成都B卷27题10分)问题背景如图①，等腰△ABC中，AB＝AC，∠BAC＝120°，作AD⊥BC于点D，则D为BC的中点，∠BAD＝ ∠BAC＝60°，于是 ＝ ＝ .迁移应用(1)如图②，△ABC和△ADE都是等腰三角形，∠BAC＝∠DAE＝120°，D，E，C三点在同一条直线上，连接BD.i)求证：△ADB≌△AEC；
(1)i)证明：∵△ABC与△ADE是等腰三角形，∴AD＝AE，AB＝AC.∵∠DAE＝∠BAC＝120°，∴∠DAE－∠BAE＝∠BAC－∠BAE，∴∠DAB＝∠EAC，∴△ADB≌△AEC(SAS)；
ii)请直接写出线段AD，BD，CD之间的等量关系式；
拓展延伸(2)如图③，在菱形ABCD中，∠ABC＝120°，在∠ABC内作射线BM，作点C关于BM的对称点E，连接AE并延长交BM于点F，连接CE，CF.i)证明△CEF是等边三角形；
(2)i)证明：如图，连接BE，过点B作BG⊥AE于点G.
∵点C，E关于BM对称，∴BE＝BC，CF＝EF，∠3＝∠4，∠EFB＝∠CFB，
在菱形ABCD中，AB＝BC，∴AB＝BC＝BE.∵BG⊥AE，∴∠1＝∠2.∵∠ABC＝120°，∴∠GBF＝∠2＋∠3＝ ∠ABC＝60°.在Rt△BGF中，∠BGF＝90°，∠GBF＝60°，则∠GFB＝30°，∴∠EFC＝2∠GFB＝60°.∵EF＝FC，∴△CEF是等边三角形；
ii)若AE＝5，CE＝2，求BF的长．
4. 在四边形ABCD中，点E，F分别是边AB，AD上的点，连接CE，CF并延长，分别交DA，BA的延长线于点H，G.(1)如图①，若四边形ABCD是菱形，∠ECF＝ ∠BCD，求证：AC2＝AH·AG；
∴∠DCG＝∠ACH，∠BCE＝∠ACG，∴∠G＝∠ACH，∠H＝∠ACG，∴△ACG∽△AHC，∴ ＝ ，∴AC2＝AH·AG；
(2)如图②，若四边形ABCD是正方形，∠ECF＝45°，BC＝4，设AE＝x，AG＝y，求y与x的函数关系式；
(2)解：如图，连接AC.
∴∠DCG＝∠ACH，∠BCE＝∠ACG，∴∠G＝∠ACH，∠H＝∠ACG，∴△ACG∽△AHC，∴ ＝ ，∴AC2＝AH·AG.∵BC＝AB＝4，∴AC＝4 ，∴y＝ .
∵BC∥AD，∴△EAH∽△EBC，∴ ＝ ，∴ ＝ ，∴AH＝ ，∴y＝ ；
连接AC，证明△ACG∽△AHC，再根据平行线性质得到△EAH∽△EBC，列出比例式求解．
(3)如图③，若四边形ABCD是矩形，AB∶AD＝1∶2，CG＝CH，∠GCH＝45°，求tan ∠AHG的值．
(3)解：如图，取BC中点M，过点M作MN∥BG，交AD于点P，交CG于点N，连接CP.
∵CG＝CH，∴CG＝CH＝2CN.∵CD∥BA，MN∥BG，∴CD∥MN∥BG，∴ ＝ ＝1∴DP＝PA.∵AB∶AD＝1∶2，∴设AB＝a＝CD，则AD＝2a＝BC，∴CM＝a＝DP，且BC∥AD，
∴四边形CDPM是平行四边形，且CD＝DP＝a，∠D＝90°，∴四边形CDPM是正方形，∴CP＝ a.∵四边形CDPM是正方形，且∠GCH＝45°，由(2)可得△CPN∽△HPC，∴ ＝ ＝ ＝2，∴PH＝2CP＝2 a，PN＝ CP＝ a，∴MN＝a＋ a，AH＝PH－PA＝2 a－a，∴BG＝2MN＝2a＋ a，