中职数学北师大版（2021）拓展模块一 上册5.3.2 抛物线的性质课文课件ppt

这是一份中职数学北师大版（2021）拓展模块一 上册5.3.2 抛物线的性质课文课件ppt，共14页。PPT课件主要包含了对称性，离心率，焦点到准线的距离为p，p＝4，＝4p，＝2p×2，＝2p×1，解得p＝2，解得p＝6等内容，欢迎下载使用。

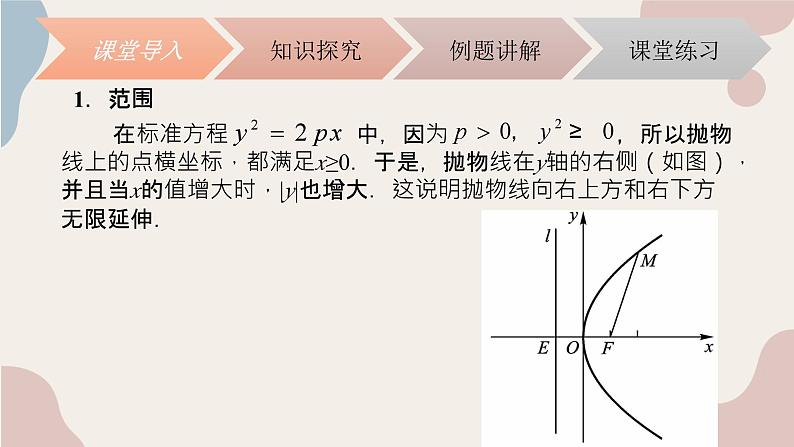
在标准方程 中，因为 ，所以抛物线上的点横坐标，都满足x≥0．于是，抛物线在y轴的右侧（如图），并且当x的值增大时，|y|也增大．这说明抛物线向右上方和右下方无限延伸．
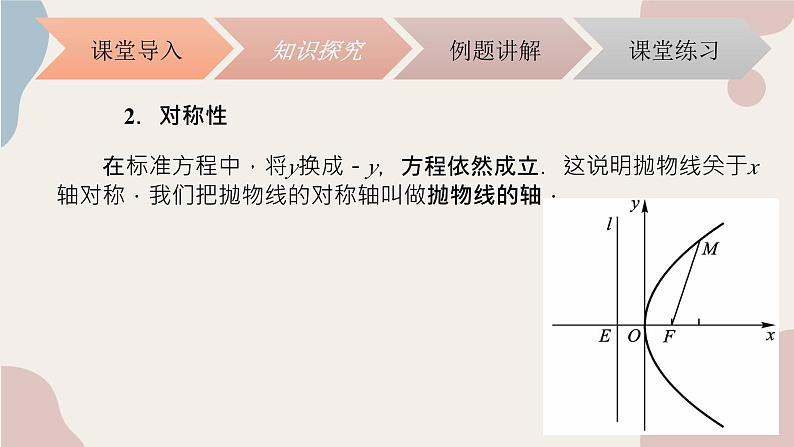
在标准方程中，将y换成－y，方程依然成立．这说明抛物线关于x轴对称．我们把抛物线的对称轴叫做抛物线的轴．
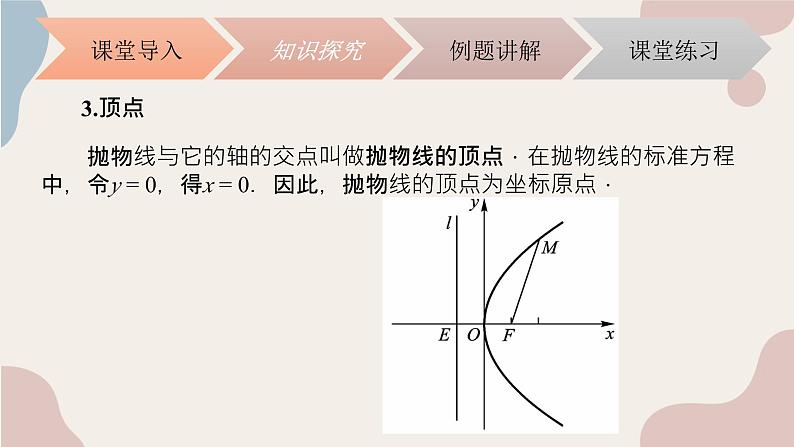
抛物线与它的轴的交点叫做抛物线的顶点．在抛物线的标准方程中，令y = 0，得x = 0．因此，抛物线的顶点为坐标原点．
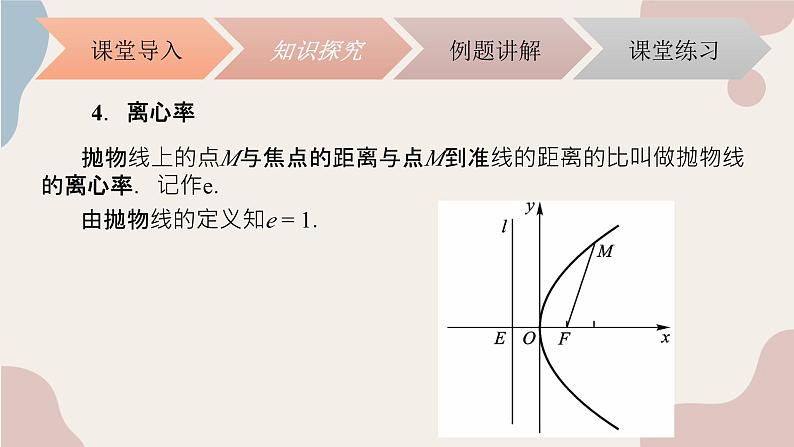
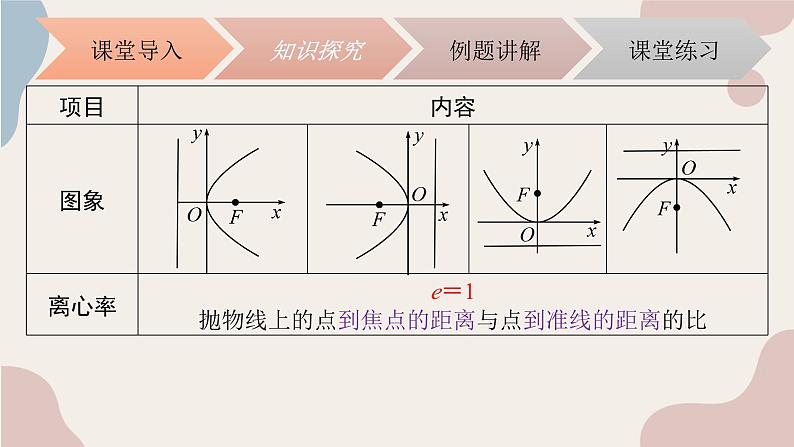
抛物线上的点M与焦点的距离与点M到准线的距离的比叫做抛物线的离心率．记作e．
由抛物线的定义知e = 1．
【例1】　抛物线y2＝8x的焦点坐标为________.
∴焦点坐标 为(2，0).
又∵焦点在x轴的正半轴上
【例2】已知抛物线的标准方程为x2＝－8y.求抛物线的焦点F的坐标、准线方程、焦点到准线的距离；
解：p＝4，且焦点在y轴的负半轴上．故抛物线的焦点F的坐标为(0，－2)，准线方程为y＝2，焦点到准线的距离是4.
【例3】　以坐标原点为顶点，x轴为对称轴，且经过点p(－2，－4)的抛物线的标准方程为(　　) A．y2＝－8x B．x2＝－y C．y2＝－8x或x2＝－y D．y2＝－x或x2＝－8y
设抛物线方程为y2＝－2px
(－4)2＝－2p×(－2)
设抛物线方程为y2＝2px①或x2＝2py②.
①抛物线方程为y2＝4x
【例4】已知抛物线的顶点为坐标原点，对称轴为坐标轴，点M(1，2)是抛物线上一点，求抛物线的标准方程．
设抛物线方程为y2＝2px
抛物线方程为y2＝4x
设抛物线方程为y2＝－2px①或x2＝2py②.
①抛物线方程为y2＝－12x
2. 已知抛物线的顶点为坐标原点，对称轴为坐标轴，并且经过点M (－3,6)，求抛物线的标准方程.