

所属成套资源:2024年全国各省市县区学校高考数学模拟试卷真题合集(含详细答案解析)
2023-2024学年云南三校高三高考备考实用性联考卷(六)数学试题(含详细答案解析)
展开
这是一份2023-2024学年云南三校高三高考备考实用性联考卷(六)数学试题(含详细答案解析),共20页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
1.设集合A=x1≤xb>0的左、右焦点,M,N是椭圆C上两点,且2MF1=3F1N,MF2⋅MN=0,则椭圆C的离心率为( )
A. 53B. 175C. 23D. 135
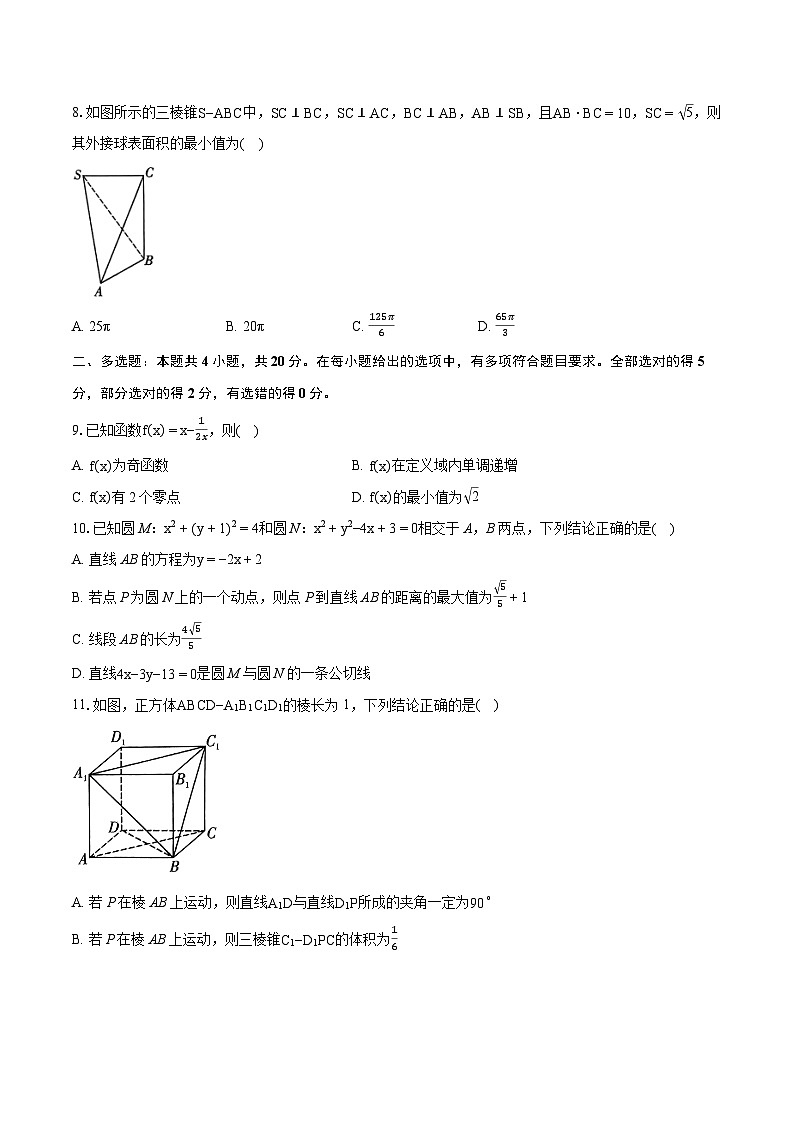
8.如图所示的三棱锥S−ABC中,SC⊥BC,SC⊥AC,BC⊥AB,AB⊥SB,且AB⋅BC=10,SC= 5,则其外接球表面积的最小值为( )
A. 25πB. 20πC. 125π6D. 65π3
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知函数fx=x−12x,则( )
A. fx为奇函数B. fx在定义域内单调递增
C. fx有2个零点D. fx的最小值为 2
10.已知圆M:x2+y+12=4和圆N:x2+y2−4x+3=0相交于A,B两点,下列结论正确的是( )
A. 直线AB的方程为y=−2x+2
B. 若点P为圆N上的一个动点,则点P到直线AB的距离的最大值为 55+1
C. 线段AB的长为4 55
D. 直线4x−3y−13=0是圆M与圆N的一条公切线
11.如图,正方体ABCD−A1B1C1D1的棱长为1,下列结论正确的是( )
A. 若P在棱AB上运动,则直线A1D与直线D1P所成的夹角一定为90∘
B. 若P在棱AB上运动,则三棱锥C1−D1PC的体积为16
C. 若P在底面ABCD内(包含边界)运动,且满足DP=1,则动点P的轨迹的长度为π
D. 若P在△ABC内(包含边界)运动,则直线D1P与平面ABCD所成角的正弦值的取值范围为 33, 63
12.已知函数fx=xlnx+mx2mx1),则下列正确的是( )
A. −120的左、右焦点,O为坐标原点,过F2作渐近线y=b 3x的垂线,垂足为P,且sin∠F1PO= 33,过双曲线C上一点Q作两渐近线的平行线分别交渐近线于M,N两点,则四边形OMQN的面积为__________.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题10分)
在锐角△ABC中,角A,B,C的对边分别为a,b,c.从条件①:sinBcsBtanB=34;条件②: 3sinB−csB 3sinB+csB=12;条件③:2ccsB−bcsA=acsB这三个条件中选择一个作为已知条件.(注:若选择多个条件作答,则只按第一个解答计分)
(1)求角B的大小;
(2)若b=3 2,∠B的平分线BD交AC于点D,且BD= 3,求△ABC的面积.
18.(本小题12分)
如图,在四棱锥E−ABCD中,平面ABCD⊥平面ABE,点E在以AB为直径的半圆O上运动(不包括端点),底面ABCD为矩形,AD=BC=12AB=1.
(1)求证:BE⊥平面ADE;
(2)当四棱锥E−ABCD体积最大时,求平面ADE与平面ACE所成夹角的余弦值.
19.(本小题12分)
已知数列an的前n项和为Sn,且Sn=n2+n+42.在数列bn中,b1=0,bn=bn−1+12n−1.
(1)求an,bn的通项公式;
(2)设cn=an1−bn,求数列cn的前n项和Tn.
20.(本小题12分)
数学中有这么一个定理:喝醉的酒鬼总能找到回家的路,喝醉的小鸟则可能永远也回不了家.这个定理数学家波利亚在1921年给出证明,它与随机游走有关,随机游走是概率论中的一个重要概念,它描述了一个在空间中随机移动的过程,随机游走最简单的形式是一维随机游走,即一个点在数轴上以一定的概率向左或向右移动,如图,一个质点在随机外力的作用下,从原点O出发,每隔1s等可能地向左或向右移动一个单位,记移动k次后质点回到原点位置的概率为pk,其中k为偶数.
(1)求p0,p2,p4;
(2)证明:2pk+2−pk≥0.
21.(本小题12分)
已知A,B,C是抛物线y2=4x上三点,且CA⊥CB,CD⊥AB,垂足为D.
(1)当C的坐标为0,0时,求点D的轨迹方程;
(2)当C的坐标为1,2时,是否存在点Q,使得DQ为定值,若存在,求出Q的坐标;若不存在,请说明理由.
22.(本小题12分)
牛顿迭代法是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法.比如,我们可以先猜想某个方程fx=0的其中一个根r在x=x0的附近,如图6所示,然后在点x0,fx0处作fx的切线,切线与x轴交点的横坐标就是x1,用x1代替x0重复上面的过程得到x2;一直继续下去,得到x0,x1,x2,…,xn.从图形上我们可以看到x1较x0接近r,x2较x1接近r,等等.显然,它们会越来越逼近r.于是,求r近似解的过程转化为求xn,若设精度为ε,则把首次满足xn−xn−10,所以fx为单调递增函数,
所以函数fx在(−∞,0),(0,+∞)单调递增,所以B错误;
对于C中,令fx=0,即x−12x=0,解得x=± 22,所以C正确;
对于D中,例如:当x=12时,f(12)=12−1=−12< 2,所以D不正确.
故选:AC.
10.【答案】BCD
【解析】【分析】
A选项,两圆作差求出相交弦方程;B选项,求出圆心N(2, 0)到直线AB的距离,从而得到点P到直线AB的距离的最大值;C选项,根据垂径定理求出弦长;D选项,利用圆心到直线的距离等于半径得到直线4x−3y−13=0是圆M与圆N的一条公切线.
【解答】
解:A选项,两圆方程作差得4x+2y−6=0,即y=−2x+3,所以两圆公共弦AB所在直线方程为y=−2x+3,A错误;
B选项,圆M的圆心为M0,−1,半径r1=2,
圆N:x2+y2−4x+3=0,即(x−2)2+y2=1的圆心为N2,0,半径r2=1;
圆心N2,0到直线AB的距离d=1 4+1= 55,半径r2=1,
所以点P到直线AB的距离的最大值为 55+1,B正确;
C选项,AB=2 12− 552=4 55,C正确;
D选项,圆心M0,−1到直线4x−3y−13=0的距离d1=10 16+9=2=r1,
圆心N(2, 0)到直线4x−3y−13=0的距离d2=5 16+9=1=r2,
所以直线4x−3y−13=0是圆M与圆N的一条公切线,D正确.
故选:BCD.
11.【答案】ABD
【解析】【分析】
证明A1D⊥平面ABC1D1,再根据线面垂直的性质即可判断A;根据VC1−D1PC=VP−D1C1C即可判断B;易得动点P的轨迹的长度为以D为圆心,1为半径的圆的周长的四分之一,即可判断C;DD1⊥平面ABCD,可得∠DPD1即为直线D1P与平面ABC所成角,再进行分析即可判断D.
【解答】
解:对于A,连接AD1,A1D,则A1D⊥AD1, AB⊥平面ADD1A1,
又A1D⊂平面ADD1A1,∴A1D⊥AB,
又AB∩AD1=A,AB⊂平面ABC1D1,AD1⊂平面ABC1D1,
∴A1D⊥平面ABC1D1,
又D1P⊂平面ABC1D1,∴A1D⊥D1P,
所以直线A1D与直线D1P所成的夹角一定为90∘,故A正确;
对于B,连接PC,PC1,D1C,
则三棱锥C1−D1PC的体积等于三棱锥P−CC1D1的体积,
∵AB//平面CDD1C1,∴点P到平面CDD1C1的距离=BC,为定值1,
即三棱锥P−CC1D1的高为1,底面三角形CD1C1的面积为12,∴VC1−D1PC=VP−D1C1C=13×12×1×1×1=16,故B正确;
对于C,因为P满足DP=1,
则动点P的轨迹的长度为以D为圆心,1为半径的圆的周长的四分之一,
所以P点的轨迹的长度为π2,故C错误;
对于D,在正方体ABCD−A1B1C1D1中,DD1⊥平面ABCD,
对于平面ABC,DD1为垂线,D1P为斜线,DP为射影,
所以∠DPD1即为直线D1P与平面ABC所成角,
设AC∩BD=O,则AC⊥BD,
因为P是△ABC内(包括边界)的动点,
所以当P与O重合时,DP=DB2= 22最小,此时sin∠DPD1=1D1P= 63,
当P与B重合时,DP=DB= 2最大,此时sin∠DPD1=1D1P= 33,
所以sin∠DPD1∈ 33, 63,故D正确.
故选:ABD.
12.【答案】ABC
【解析】【分析】
利用函数有两个极值点得m的范围判断A,,并判断出00,
解得−120,f(x)为增函数,
当x∈(π,2π)时,f′(x)0,所以pk+2−12pk>0,即2pk+2−pk>0,
综上,2pk+2−pk≥0.
【解析】(1)根据题意,得到质点向左或向右的均为概率为12,进而求得p0,p2,p4的值;
(2)法一:设k=2n(n∈N*),则pk=p2n=(2n)!n! ⋅ n!⋅122n,pk+2=(2n+2)!(n+1)! ⋅ (n+1)!⋅122n+2,求得pk+2pk=1−12n+2,进而得到pk+2pk≥12,即可得到2pk+2−pk≥0.
法二:设k=2n(n∈N*),求得pk=p2n=C2nn122n,pk+2=p2n+2=C2n+2n+1122n+2,化简得到pk+2=p2n+2=12pk+(C2nn+1+C2nn−1)122n+2,结合(C2nn+1+C2nn−1)⋅122n+2>0,即可得证.
21.【答案】解:(1)设Ax1,y1,Bx2,y2,直线AB的方程为x=my+bb≠0.
联立y2=4x,x=my+b得y2−4my−4b=0,则y1+y2=4m,y1y2=−4b①,
因为CA⊥CB,所以CA • CB=0,即x1x2+y1y2=0,
所以(my1+b)(my2+b)+y1y2=0②,
由①②得:m2+1y1y2+mby1+y2+b2=0,整理得b2−4b=0,
因为b≠0,所以b=4,直线AB恒过定点4,0,
设点Dx,y,则kCD • kAB=−1,即yx • yx−4=−1,整理得(x−2)2+y2=4,
所以点D的运动轨迹为以2,0为圆心,半径为2的圆(原点除外).
(2)由(1)因为CA⊥CB,
所以CA • CB=0,CA=x1−1,y1−2,CB=x2−1,y2−2,
则CA • CB=x1x2−(x1+x2)+1+y1y2−2(y1+y2)+4
=116y1y22+y1y2−m+2y1+y2−2b+5=0③,
将①代入③得:b2−6b−4m2−8m+5=0,
(b−3)2=4(m+1)2得,b−3=2(m+1)或者b−3=−2(m+1).
当b−3=2(m+1)时,直线AB过P5,−2.
当b−3=−2(m+1)时,直线AB过1,2,此时C在AB上,不合题意.
所以直线AB恒过P5,−2.
因为C为定点,所以CP为定值,
在Rt△CPD中取CP中点Q,连接DQ,|DQ|=12|CP|,
所以|DQ|为定值.
此时Q的坐标为3,0,
故存在点Q3,0,使得|DQ|为定值.
【解析】(1)设直线AB的方程为x=my+b,与抛物线联立,由CA⊥CB得直线过定点,再利用CD⊥AB求出轨迹方程;
(2)同(1)的方法,先求出直线AB恒过P5,−2,再利用直角三角形和圆的意义,求出定点和定值.
22.【答案】解:(1)因为f(x)=x3−x+1,则f′(x)=3x2−1,
k1=f′(−1)=2,f−1=1,曲线f(x)在x0=−1处的切线为y−1=2(x+1)⇒x1=−1.5,且|x1−x0|≥0.5,
k2=f′(−1.5)=234,f−1.5=−78,曲线f(x)在x1=−1.5处的切线为y+78=234x+32⇒x2=−3123≈−1.35,且|x2−x1|0,即3x2−1>0,得x> 33或x
相关试卷
这是一份2024届云南三校高考备考实用性联考卷(六)数学试题及答案,文件包含2024届云南三校高考备考实用性联考卷六数学试卷pdf、2024届云南三校高考备考实用性联考卷六数学-答案pdf、2024届云南三校高考备考实用性联考卷六数学-双向细目表pdf等3份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
这是一份2024云南省三校高三高考备考实用性联考卷(六)数学PDF版含解析,共16页。
这是一份2023-2024学年云南省三校高三高考备考实用性联考卷(五)数学试题(含解析),共19页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。









