广东省深圳市中国科学院深圳先进技术研究院实验学校2023-2024学年九年级上学期数学期末试卷

这是一份广东省深圳市中国科学院深圳先进技术研究院实验学校2023-2024学年九年级上学期数学期末试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

第Ⅰ卷 客观题
第Ⅰ卷的注释
一、选择题（本题有10小题，每题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确的选项用2B铅笔填涂在答题卡上）(共10题；共30分)
1. 如图所示，该几何体的主视图是（ ）
2. 已知关于x的方程的一个根为 ， 则实数m的值为（ ）
3. 下列平行四边形中，根据图中所标出的数据，不能判定是菱形的是（ ）
4. 如图，在平面直角坐标系中，两个“E”字是位似图形，位似中心点O ， ①号“E”与②号“E”的位似比为.点在①号“E”上，则点P在②号“E”上的对应点Q的坐标为（ ）
5. 近几年，二维码逐渐进入了人们的生活，成为广大民众生活中不可或缺的一部分，小刚将二维码打印在面积为20的正方形纸片上，如图，为了估计黑色阴影部分的面积，他在纸内随机掷点，经过大量重复实验，发现点落在黑色阴影的频率稳定在左右，则据此估计此二维码中黑色阴影的面积为（ ）
6. 如图，嘉嘉在A时测得一棵高的树的影长为 ， 若A时和B时两次日照的光线互相垂直，则B时的影长为（ ）
7. 下面说法正确的是（ ）
8. 近年来，由于新能源汽车的崛起，燃油汽车的销量出现了不同程度的下滑，经销商纷纷开展降价促销活动.某款燃油汽车今年3月份售价为23万元，5月份售价为16万元，设该款汽车这两月售价的月均下降率是x ， 则所列方程正确的是（ ）
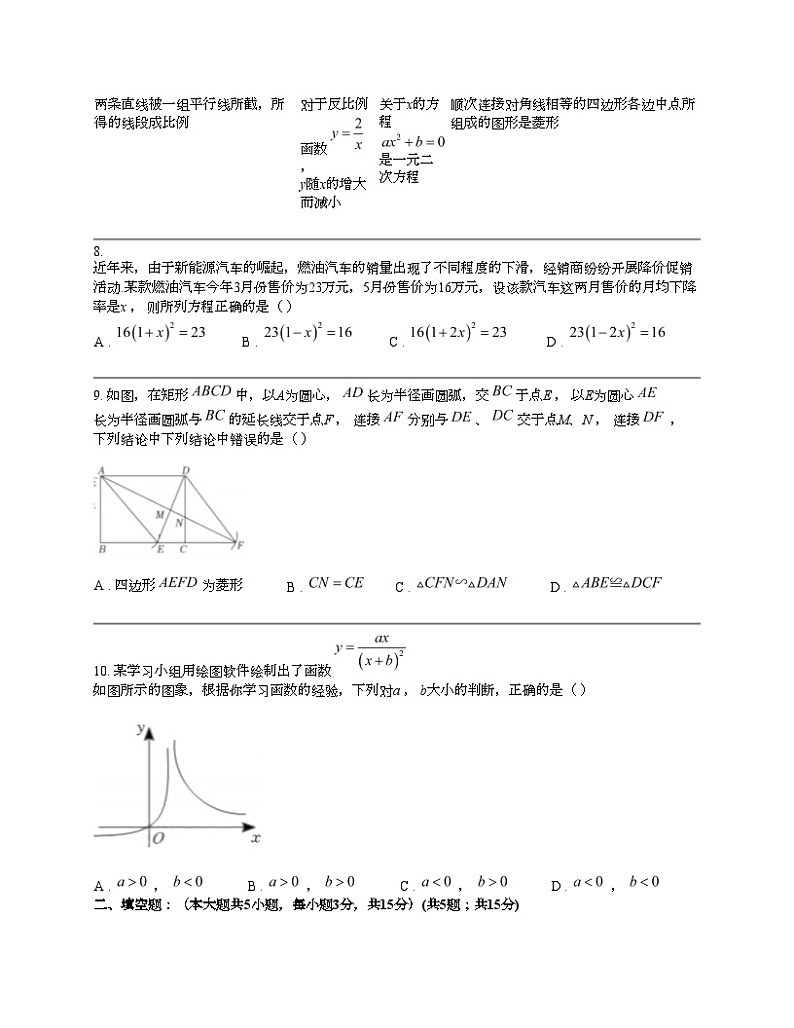
9. 如图，在矩形中，以A为圆心，长为半径画圆弧，交于点E ， 以E为圆心长为半径画圆弧与的延长线交于点F ， 连接分别与、交于点M、N ， 连接 ， 下列结论中下列结论中错误的是（ ）
10. 某学习小组用绘图软件绘制出了函数如图所示的图象，根据你学习函数的经验，下列对a ， b大小的判断，正确的是（ ）
二、填空题：（本大题共5小题，每小题3分，共15分）(共5题；共15分)
11. 若 ， 则____________________.
12. 大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”的美，如图，点P为的黄金分割点.如果的长度为 ， 那么的长度为____________________.
13. 如图，在△ABC中，∠ABC＝90°，∠A＝60°，直尺的一边与BC重合，另一边分别交AB，AC于点D，E．点B，C，D，E处的读数分别为15，12，0，1，则直尺宽BD的长为____________________．
14. 如图，在矩形中， ， ， F是上的一个动点（F不与A ， B重合），过点F的反比例函数的图象与边交于点E ， 若时，则____________________.
15. 如图，为直角三角形， ， ， ， D是边上的中点，将绕着点A逆时针旋转，使点C落在线段上的点E处，点B的对应点为F ， 边与边交于点G ， 则的长是____________________.
第Ⅱ卷 主观题
第Ⅱ卷的注释
三、解答题：（本题共7小题，其中第16题6分，第17题6分，第18题8分，第19题8分，第20题8分，第21题9分，第20题10分，共55分）(共7题；共55分)
16. 解下列方程：
（1） ；
（2） .
17. 已知：的两邻边 ， 的长是关于x的方程的两个实数根.
（1） 当m为何值时，是菱形？
（2） 若的长为3，求的周长.
18. 某校在九年级随机抽取了20名学生分成甲、乙两组，每组各10人，进行“网络安全”知识竞赛，把甲、乙两组的成绩进行整理分析（满分100分，竞赛得分用x表示：为网络安全意识非常强，为网络安全意识比较强，为网络安全意识一般）.收集
根据以上信息回答下列问题：
（1） 填空：a=____________________，b=____________________，c=____________________；
（2） 已知该校九年级有500人，估计九年级网络安全意识非常强的人数一共是多少？
（3） 现在准备从甲乙两组满分人数中抽取两名同学参加全区比赛，用树状图或者列表法求抽取的两名同学恰好一人来自甲组，另一人来自乙组的概率.
19. 如图，在正方形中，点E ， F分别在 ， 上， ， 垂足为M.
（1） 求证：；
（2） 若正方形的边长是8， ， 点N是的中点，求的长.
20. 园林部门计划在公园建一个如图（甲）所示的长方形花圃 ， 花圃的一面靠墙（墙足够长），另外三边用木栏围成， ， 建成后所用木栏总长120米，在图（甲）总面积不变的情况下，在花圃内部设计了一个如图（乙）所示的正方形网红打卡点和两条宽度相等的小路，其中，小路的宽度是正方形网红打卡点边长的 ， 其余部分种植花卉，花卉种植的面积为1728平方米.
（1） 求长方形花圃的长和宽；
（2） 求出网红打卡点的面积.
21. 【综合与实践】：北师大版九年级上册数学教材第122页第21题：“怎样把一块三角形的木板加工成一个面积最大的正方形桌面？”某小组同学对此展开了思考.
（1） 【特例感知】：若木板的形状是如图（甲）所示的直角三角形， ， ， 根据“相似三角形对应的高的比等于相似比”可以求得此时正方形的边长是____________________.
（2） 【问题解决】：若木板是面积仍然为的锐角三角形 ， 按照如图（乙）所示的方式加工，记所得的正方形的面积为S ， 如何求S的最大值呢？某学习小组做了如下思考：
设 ， 、边上的高 ， 则 ， ∴ ， 由-得： ， 从而可以求得 ， 若要内接正方形面积S最大，即就是求x的最大值。因为为定值，因此只需要分母最小即可.
小组同学借鉴研究函数的经验，令.探索函数的图象和性质：
①下表列出了y与a的几组对应值，其中 ▲ ；
②在如图（丙）所示的平面直角坐标系中画出该函数的大致图象；
③结合表格观察函数图象，以下说法正确的是 ▲ .
A.当时，y随a的增大而增大.
B.该函数的图象可能与坐标轴相交.
C.该函数图象关于直线对称.
D.当该函数取最小值时，所对应的自变量a的取值范围在之间.
22. 某数学学习小组学习完四边形后进行了如下探究，已知四边形为矩形，请你帮助他们解决下列问题：
（1） 【初步尝试】：他们将矩形的顶点E、G分别在如图（1）所示的的边、上，顶点F、H恰好落在的对角线上，求证：：
（2） 【深入探究】：如图2，若为菱形， ， 若 ， 求的值；
（3） 【拓展延伸】：如图（3），若为矩形，；且 ， 请直接写出此时的值是（用含有m ， n的代数式表示）.
A .
B .
C .
D .
A . 4
B .
C . 3
D .
A .
B .
C .
D .
A .
B .
C .
D .
A . 8
B . 12
C .
D .
A .
B .
C .
D .
A . 两条直线被一组平行线所截，所得的线段成比例
B . 对于反比例函数 ， y随x的增大而减小
C . 关于x的方程是一元二次方程
D . 顺次连接对角线相等的四边形各边中点所组成的图形是菱形
A .
B .
C .
D .
A . 四边形为菱形
B .
C .
D .
A . ，
B . ，
C . ，
D . ，
平均数
中位数
众数
甲组
a
80
80
乙组
83
b
c
a
…
1
2
3
4
…
y
…
m
4
4
…