

广东省深圳市龙华实验学校2023-2024学年九上数学期末经典模拟试题含答案
展开这是一份广东省深圳市龙华实验学校2023-2024学年九上数学期末经典模拟试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,中,,,,的值为,对于抛物线,下列说法中错误的是等内容,欢迎下载使用。
学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
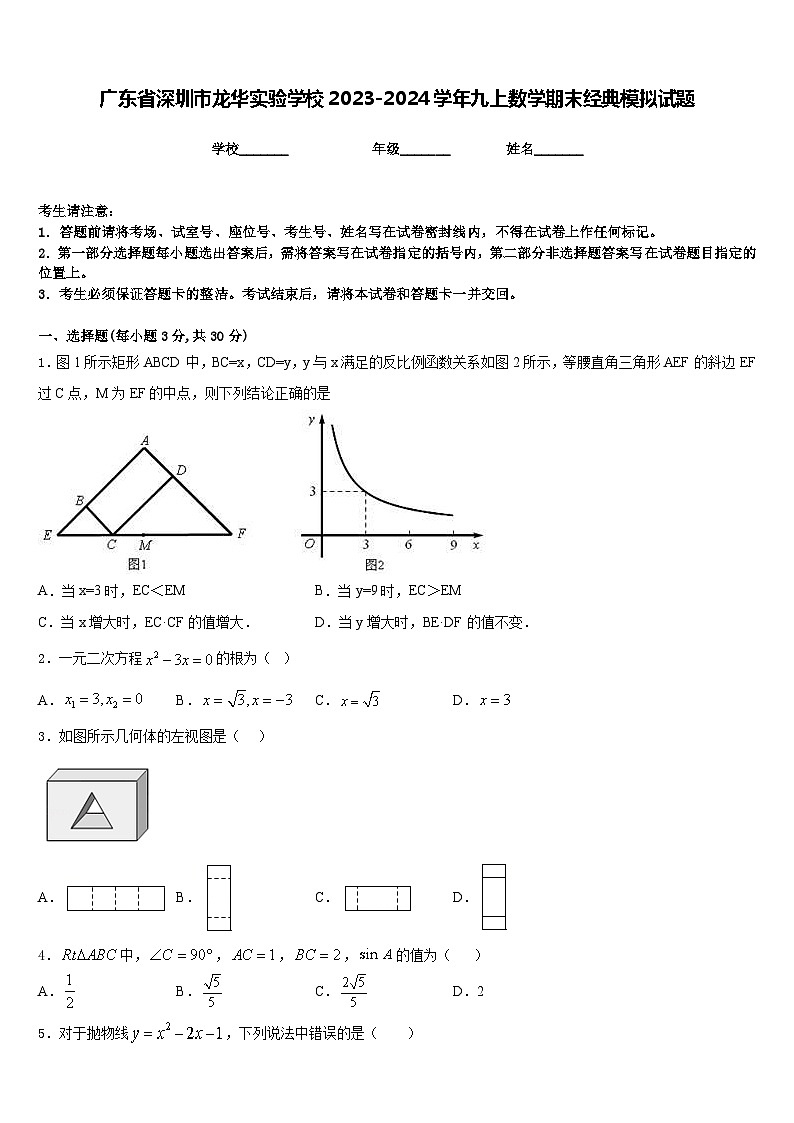
1.图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是
A.当x=3时,EC<EMB.当y=9时,EC>EM
C.当x增大时,EC·CF的值增大.D.当y增大时,BE·DF的值不变.
2.一元二次方程的根为( )
A.B.C.D.
3.如图所示几何体的左视图是( )
A.B.C.D.
4.中,,,,的值为( )
A.B.C.D.2
5.对于抛物线,下列说法中错误的是( )
A.顶点坐标为
B.对称轴是直线
C.当时,随的增大减小
D.抛物线开口向上
6.分别写有数字﹣4,0,﹣1,6,9,2的六张卡片,除数字外其它均相同,从中任抽一张,则抽到偶数的概率是( )
A.B.C.D.
7.已知点是线段的黄金分割点,且,,则长是( )
A.B.C.D.
8.某种工件是由一个长方体钢块中间钻了一个上下通透的圆孔制作而成,其俯视图如图所示,则此工件的左视图是 ( )
A.B.C.D.
9.抛物线的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为,则b、c的值为
A.b=2,c=﹣6B.b=2,c=0C.b=﹣6,c=8D.b=﹣6,c=2
10.如图,,,,四点都在上,,则的度数为( )
A.B.C.D.
二、填空题(每小题3分,共24分)
11.如图,在由边长为1的小正方形组成的网格中.点 A,B,C,D 都在这些小正方形的格点上,AB、CD 相交于点E,则sin∠AEC的值为_____.
12.因式分解x3-9x=__________.
13.如图,矩形ABCD中,AB=1,AD=.以A为圆心,AD的长为半径做弧交BC边于点E,则图中的弧长是_______.
14.如图,为半圆的直径,点、、是半圆弧上的三个点,且,,若,,连接交于点,则的长是______.
15.在某一时刻,测得一根高为2m的竹竿的影长为1m,同时测得一栋建筑物的影长为12m,那么这栋建筑物的高度为_____m.
16.如图所示,个边长为1的等边三角形,其中点,,,,…在同一条直线上,若记的面积为,的面积为,的面积为,…,的面积为,则______.
17.已知二次函数y=a(x+3)2﹣b(a≠0)有最大值1,则该函数图象的顶点坐标为_____.
18.将量角器按如图所示的方式放置在三角形纸板上,使点在半圆上,点、的度数分别为、,则的大小为___________
三、解答题(共66分)
19.(10分)如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC边于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,
(1)试证明:△AEP∽△ABC;
(2)求y与x之间的函数关系式.
20.(6分)如图,抛物线过点,,直线交抛物线于点,点的横坐标为,点是线段上的动点.
(1)求直线及抛物线的解析式;
(2)过点的直线垂直于轴,交抛物线于点,求线段的长度与的关系式,为何值时,最长?
(3)是否存在点使为等腰三角形,若存在请直接写出点的坐标,若不存在,请说明理由.
21.(6分)如图1,已知点A(a,0),B(0,b),且a、b满足+(a+b+3)2=0,平等四边形ABCD的边AD与y轴交于点E,且E为AD中点,双曲线y=经过C、D两点.
(1)a= ,b= ;
(2)求D点的坐标;
(3)点P在双曲线y=上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点Q的坐标;
(4)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
22.(8分)如图,矩形ABCD中,AB=3,BC=5,CD上一点E,连接AE,将△ADE绕点A旋转90°得△AFG,连接EG、DF.
(1)画出图形;
(2)若EG、DF交于BC边上同一点H,且△GFH是等腰三角形,试计算CE长.
23.(8分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元.如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
24.(8分)如图,,平分,且交于点,平分,且交于点,与相交于点,连接
求的度数;
求证:四边形是菱形.
25.(10分)如图,已知方格纸中的每个小方格都是相同的正方形(边长为1),方格纸上有一个角∠AOB,A,O,B均为格点,请回答问题并只用无刻度直尺和铅笔,完成下列作图并简要说明画法:(1)OA=_____,(2)作出∠AOB的平分线并在其上标出一个点Q,使.
26.(10分)小明想要测量一棵树DE的高度,他在A处测得树顶端E的仰角为30°,他走下台阶到达C处,测得树的顶端E的仰角是60°.已知A点离地面的高度AB=2米,∠BCA=30°,且B,C,D三点在同一直线上.求树DE的高度;
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、B
4、C
5、C
6、D
7、C
8、A
9、B
10、C
二、填空题(每小题3分,共24分)
11、
12、x(x+3)(x-3)
13、π
14、
15、1.
16、
17、 (﹣3,1)
18、
三、解答题(共66分)
19、(1)见解析;(2)y=.(0<x<6.4)
20、(1),;(2)当时,线段的长度有最大值,最大值为;(3)存在,,,
21、(1)﹣1,﹣2;(2)D(1,4);(3)Q1(0,6),Q2(0,﹣6),Q3(0,2);(4)不变,的定值为,证明见解析
22、(1)见解析;(2)CE=3-
23、第二个月的单价应是70元.
24、 (1);(2)见解析.
25、5
26、树DE的高度为6米.
相关试卷
这是一份2023-2024学年广东省龙华新区数学九上期末经典模拟试题含答案,共8页。试卷主要包含了如图,平面直角坐标系中,点E等内容,欢迎下载使用。
这是一份广东省深圳市宝安、罗湖、福田、龙华四区2023-2024学年数学八上期末经典模拟试题含答案,共6页。试卷主要包含了下列命题是真命题的是,下列二次根式中的最简二次根式是等内容,欢迎下载使用。
这是一份2023-2024学年广东省深圳市宝安、罗湖、福田、龙华四区八上数学期末监测模拟试题含答案,共7页。试卷主要包含了如图,,则图中全等三角形共有,如图,在中,,,则的度数为,若分式的值为零,则x=,周长38的三角形纸片等内容,欢迎下载使用。












