
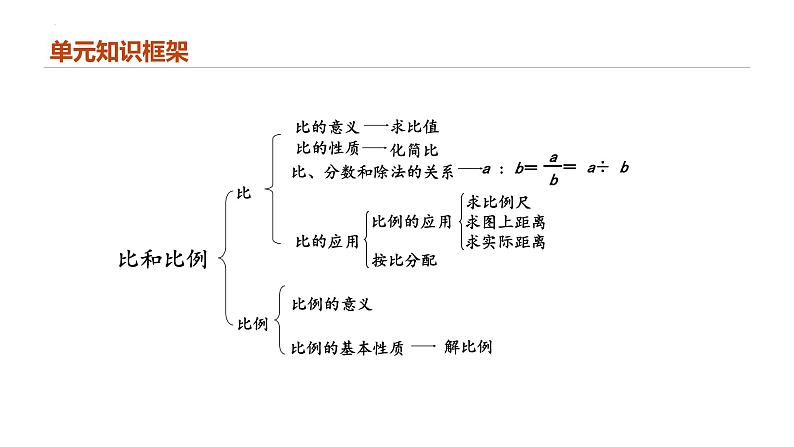




专题六:数与代数《比和比例》(复习课件)-六年级数学下学期期末核心考点集训(人教版)
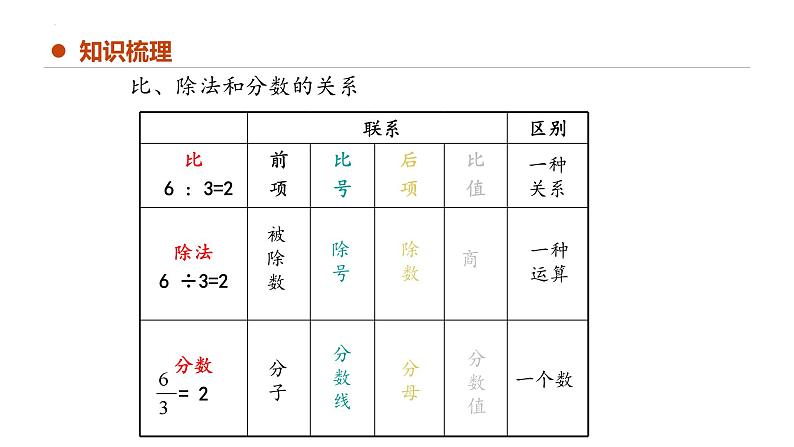
展开两个数相除又叫做两个数的比。
比的前项除以后项所得的商,叫做比值。
例如: 5÷6 可记作 5∶6。
例如:5÷6 = →就是5:6的比值。
——是借助于除法的概念建立的。
比与除法和分数的关系
比的前项相当于分数的分子和除式中的被除数;比的后项相当于分数的分母和除式中的除数;比值相当于分数的分数值和除式中的商
a :b = a÷b = (b≠0)
例:两辆汽车在公路上行驶,甲车行了75千米,耗油10升,乙车行了60千米,耗油9升。
75千米:10升=7.5千米/升表示甲车每升汽油能行7.5千米。
60千米:75千米= ,表示乙车行的路程是甲车的 。
表示倍数关系或几分之几。
在含盐5%的盐水中,盐与水的质量比写成最简整数比是( )。
分析:在5%的盐水中盐与盐水的比是5:100,盐与水的比是5:(100-5)=5:95=1:19。
三个数的平均数是13,这三个数的比是1/2:2/3:1,这三个数中最大的是( )。
分析:三个数的比是1/2:2/3:1,化简为3:4:6,则最大的数占总数的 6/3+4+6,三个数的总数是13x3=39,所以三个数中最大的数是39x6/ 3+4+6 =18。
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
利用商不变性质,我们可以进行除法的简算,也可以把小数除法变为整数除法计算。根据分数的基本性质,我们可以把分数约分成最简分数。
应用比的基本性质,我们可以把比化成最简整数比。
根据比的意义,用前项除以后项。
是一个数,可以是整数、小数或分数。
根据比的基本性质,把比的前项和后项同时乘或除以相同的数(0除外)。
是一个比,它的前项和后项是互质数(两个互质的整数比)。
前、后项同时除以它们的最大公因数
前、后项同时扩大相同的倍数
前、后项同时乘上两个分母的最小公倍数
=(32÷16) : (16÷16)
=(48÷8) : (40÷8)
怎样化简整数比? 比的前、后项都除以它们的最大公因数→最简比。
求比值:32 : 16;48 : 40
=(0.15×100) : (0.3×100)
怎样化简小数比?比的前、后项都扩大相同的倍数→整数比→最简比。
=(15÷15) : (30÷15)
=(0.75×100)︰(2×100)
= (75÷25)︰(200÷25)
= 75︰200
怎样化简分数比?比的前、后项都乘它们分母的最小公倍数→整数比→最简比。
在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。这种分配的方法通常叫做按比例分配。
●特点: 已知总量和部分量的比,求各部分量是多少。
●解题方法: 先求总份数,再求个部分量占总量的几分之几,最后用总量乘以这个几分之几,求出个部分量。
例:将这两种浓缩液混在一起制成新的清洁液,那么这种新的清洁液中浓缩液是清洁液的百分之几?(百分号前保留一位小数)
250ml 500ml
浓缩液是清洁液的百分之几?
150÷750×100% ≈33.3%
250+500=750(ml)
例:3克的蚂蚁能搬动45克的物体;3吨的大象能拉动4.5吨的物体,蚂蚁和大象谁的力气大?(要求:用学过的知识说明你的观点,回答要全面)
从物体的重量与动物本身的重量的比或比值看是蚂蚁的力气大,但是如果从动物驮的物体的重量来看是大象的力气大。
3:45 =1:15 或 45:3=153:4.5 =1:1.5 4.5:3=1.5
表示两个比相等的式子叫做比例。
例如:2.4 ∶1.6 = 60 ∶40
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
例:将上题中的平行四边形按照一定比例缩小,画在平面图上,量得图上平行四边形的底是3厘米,高是2厘米。那么图上平行四边形的底与实际底的比是( ),我们把这个比叫做( );这个比还和( )和( )的比相等,组成的比例是( )。
长方形面积的 =
S1:S2 =12:5
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
如果a:b=c:d,那么ad=bc。
【例】甲、乙两数的比是3:7,如果甲数加上6,要使比值不变,乙数应加上多少?
【解析】甲、乙两数的比是3:7,如果甲数加上6后,甲数为6+3=9,可知甲数由原来的3到现在的9,扩大到原来的3倍,要使比值不变,根据比的基本性质,比的后项也应扩大到原来的3倍,所以乙数也应扩大到原来的3倍,即7×3=21,因此乙数应加上21-7=14。
【解答】 (3+6)÷3=33×7-7=14
例:在一个比例里,两个外项为互倒数,其中一个内项是 ,另一个内项是( )。
当x=( )时,0.9∶x和3∶2能组成比例。
( )
0 100 200 300千米
实质上是一种比,是图上距离与实际距离的比。
【例】在一幅图上距离3cm代表实际距离360km的地图上,量得A,B两地相距8cm,A、B两地的实际距离是多少千米?
【解析】本题考查求比例尺及根据比例尺和图上距离求实际距离。先求出这幅地图的比例尺,再求出A,B两地的实际距离。
在一幅比例尺为1:500的地图上,量得一间教室的长是3cm,宽是2cm,求这间教室的实际占地面积。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值(商)一定,这两种量就叫做成正比例的量,它们之间的关系叫做正比例关系。 如果用x和y表示两种相关联的量,用k表示它们的比值,那么上面这种数量关系式可以用 (一定) 来表示。
两种相关联的量,一种量变化,另一种量也随着变化 ,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。 如果用x和y表示两种相关联的量,用k表示它们 的乘积,那么上面这种数量关系式可以用xy=k (一定)来表示
【解答】(1)× (2)× (3)√
下面两种量,是否成比例?如果成比例,成什么比例?并说明理由。 (1)汽车的速度一定,它行驶的路程和时间。 (1) 成正比例 (2)三角形的面积一定,三角形的底和高。 (2) 成反比例 (3)长方形的周长一定,它的长和宽。 (3)不成比例
1.判断(对的画“√”,错的画“×”)1.化简比的依据是比例的基本性质。 ( )2.比值是2的比有无数个。 ( )3.比的前项和后项同时乘或除以相同的数,比值不变, ( )4.如果a:b=8:5,那么a=8,b=5。 ( )5.甲数的 等于乙数的 (甲数、乙数均不为0),则甲数与乙数的比是9:7。( )
【解答】 1.√ 2.√ 3.× 4.× 5.√
2.小龙今年5岁,小龙的爸爸今年38岁,6年后小龙与爸爸的年龄的最简整数比是多少?
【解答】(6+5):(38+6)=1:4答:6年后小龙与爸爸的年龄的最简整数比是1:4。
3.运一批货物,每天运的吨数和需要的天数如下表。1.写出几组这两个量中对应的两个数的积,并比较积的大小。2.这个积表示什么?3.表中相关联的两个量成反比例吗?为什么?
【解答】1. 300×1=300 150×2=300 100×3=300 积相等2.答:积表示这批货物的总吨数。3.答:成反比例。因为对应两个量的积一定。
4.芳芳家新买了一辆家用小轿车,其油箱可以装40L油,小轿车行驶一段路程后,油箱中的剩余油量与行驶时间的关系如右图:(1)小轿车行驶2小时用去了( )L油。(2)一箱油够连续行驶( )h。
【解答】(1)10 (2)8
5.学校将200粒太空种子按2:3:5分配给四、五,六年级同学种植,四、五、六年级各分到太空种子多少粒?
6.在比例尺是1:2500000的地图上,量得甲、乙两城之间的距离是7.2cm。一辆汽车从甲城到乙城,平均每小时行80km,需要多少小时?
专题六:数与代数《数的运算》(复习课件)-六年级数学下学期期末核心考点集训(人教版): 这是一份专题六:数与代数《数的运算》(复习课件)-六年级数学下学期期末核心考点集训(人教版),共30页。PPT课件主要包含了数的运算,运算法则,四则运算的意义,四则运算法则,运算定律,运算的顺序等内容,欢迎下载使用。
专题六:数与代数《数的认识》(复习课件)-六年级数学下学期期末核心考点集训(人教版): 这是一份专题六:数与代数《数的认识》(复习课件)-六年级数学下学期期末核心考点集训(人教版),共36页。PPT课件主要包含了小数的概念,小数的基本性质,小数的分类,甲是乙的10倍,分数的概念,分数的基本性质,比较大小,百分数等内容,欢迎下载使用。
专题六:数与代数《式与方程》(复习课件)-六年级数学下学期期末核心考点集训(人教版): 这是一份专题六:数与代数《式与方程》(复习课件)-六年级数学下学期期末核心考点集训(人教版),共29页。PPT课件主要包含了式与方程,等式与方程,列方程解决实际问题,用字母表示数,用字母表示运算律,b+10,x-24,比a多3的数,比a少3的数,个a相加的和等内容,欢迎下载使用。













