2024年山东省烟台市中考数学模拟押题预测试卷+

这是一份2024年山东省烟台市中考数学模拟押题预测试卷+，文件包含2024年山东省烟台市中考数学模拟押题预测试卷docx、参考答案docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，选出符合题目要求的一项。
1.下列四个数字中，绝对值最小的是( )
A. −2B. −3C. 1D. 12
2.新时代中国科技事业蓬勃发展，清华大学团队首次制备出亚1纳米栅极长度的晶体管，实现等效的物理栅长为0.34纳米，将数据0.00000000034米用科学记数法表示为( )
A. 3.4×10−9B. 0.34×10−9C. 3.4×10−10D. 0.34×10−10
3.下列运算正确的是( )
A. 2a2+3a3=5a5B. a2⋅a3=a6C. a6÷a3=a3D. (a3)2=a9
4.窗花是中国传统民间艺术之一，下列四个窗花作品既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5.如图，已知线段AB=6，分别以点A，B为圆心，大于12AB长为半径画弧，两弧相交于点E，F，作直线EF交AB于点D，在直线EF上取一点C使CD=AB，连接AC、BC，点G为AC的中点，连接DG，则△ADG的周长是( )
A. 10 B. 9 C. 3 5+3 D. 3 5+2
6.如图，直线a//b，直角三角形如图放置，∠DCB=90°，若∠1=128°.则∠2的度数为( )
A. 38° B. 30° C. 28° D. 26°
7.为了解某小区居民用水情况，随机抽查了10户家庭的月用水量，结果如下表，则关于这10户家庭月用水量数据组的说法，错误的是( )
A. 中位数是5B. 众数是5C. 方差是6D. 平均数是5
8.莴笋是一种营养价值极高的蔬菜.实践小组观察记录了莴笋的成长过程，如图表示莴笋苗的成长高度y(cm)与观察时间x(天)的函数图象，则莴笋成长的最大高度是( )
A. 25cmB. 32cmC. 35cmD. 40cm
9.如图，直线y=x−4与y轴、x轴分别交于点A、B，点C为双曲线y=kx上一点，OC//AB，连接BC交双曲线于点D，点D恰好是BC的中点，则k的值是( )
A. 169 B. 2 C. 4 D. 43
10.如图，抛物线y=ax2+bx+c与x轴交于点A(−1,0)，顶点坐标(1,n)，与y轴的交点在(0,2)，(0,3)之间(包含端点)，则下列结论：①3a+b<0；②−1≤a≤−23；③对于任意实数m，a(m2−1)+b(m−1)≤0总成立；④关于x的方程ax2+bx+c=n+1有两个相等的实数根.其中结论正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
二、填空题：本题共6小题，每小题3分，共18分。
11.分解因式：x2−4y2+x−2y= ______．
12.计算：(13)−1+(2024−π)0−sin60°= ______．
13.“让孩子变聪明的方法，不是补课，不是增加作业量，而是阅读、阅读、再阅读”.某学校坚持开展阅读活动，学生人均阅读量从2021年的100万字，增加到2023年的121万字，则该校人均阅读量年均增长率为______．
14.如图，AB是⊙O的直径，点E，C在⊙O上，点A是EC的中点，过点A画⊙O的切线，交BC的延长线于点D，连接EC.若∠ADB=58.5°，则∠ACE的度数为______．
（14题） （15题） （16题）
15.如图，在平面直角坐标系中，△ABC是以点C为直角顶点的直角三角形，且AC=BC，点A的坐标为(−2,0)，点B的坐标为(0,8)，则点C的坐标为______．
16.如图，在四边形ABCD中，∠ABC=∠BAD=90°，AB=12，AD=10，AD三、解答题：本题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题6分)
[阅读理解]
在解方程组或求代数式的值时，可以用整体代入或整体求值的方法，化繁为简．
(1)解方程组x+2(x+y)=3①x+y=1②．
解：把②代入①得，x+2×1=3，解得x=1．
把x=1代入②得y=0，
所以方程组的解为x=1y=0．
(2)已知x+3y+5z=30①9x+7y+5z=10②，求x+y+z的值．
解：①+②，得10x+10y+10z=40，③
③÷10，得x+y+z=4．
[类比迁移]
(1)求方程组3(a−b)+4=2aa−b=2的解．
(2)若6x+5y+z=82x+y−3z=4，求x+y+z的值．
18.(本小题7分)
综合与实践
不借助科学计算器，如何求tan22.5°的值？小明进行了如下的实践操作：
如图，已知正方形纸片ABCD．
第一步：将正方形纸片ABCD沿AC折叠，展开后得到折痕AC．
第二步：将AB折叠到AF，使点B的对应点F恰好落在AC上，展开后得到折痕AE，点E在线段BC上，连接EF．
问题解决：
(1)求证：∠BAE=22.5°；
(2)请利用小明的实践操作过程，求tan22.5°的值．
19.(本小题8分)
每年3月最后一周的星期一为全国中小学生的安全教育日，无锡市某校为加强学生安全意识，组织了全校1600名学生参加安全知识竞赛，从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题．
(1)这次抽取了______名学生的竞赛成绩进行统计，其中：n= ______．
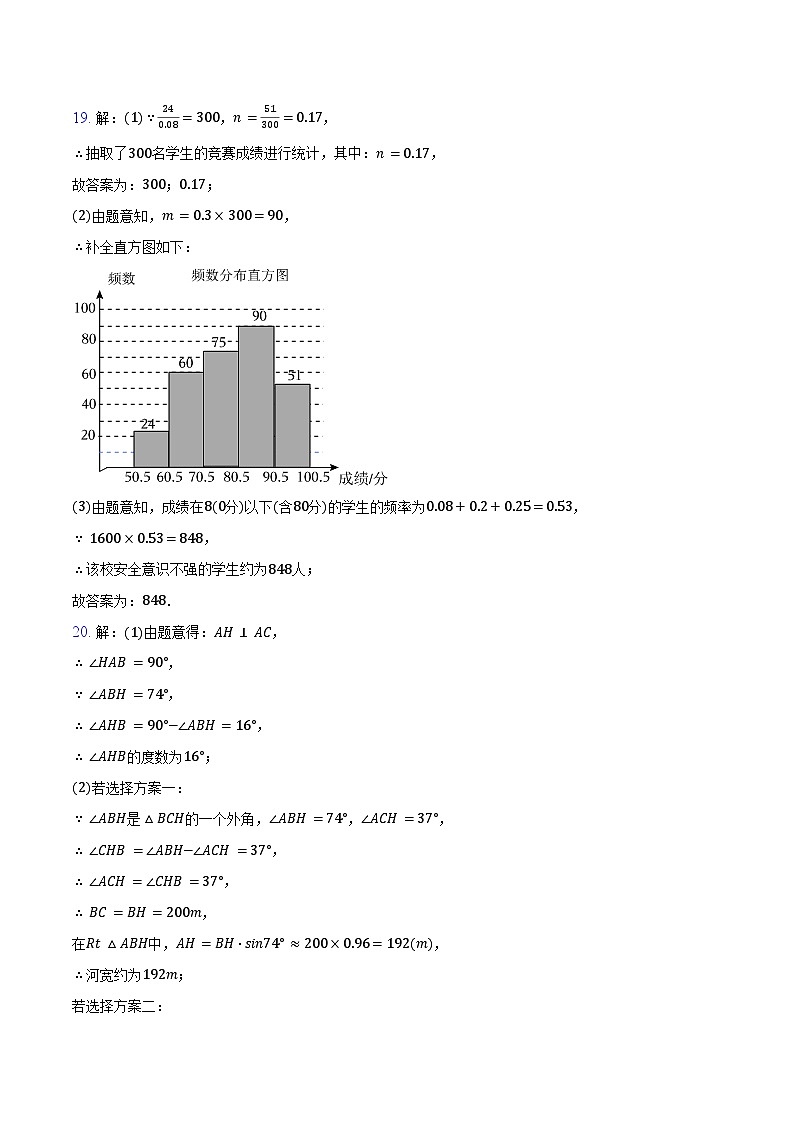
(2)补全频数分布直方图．
(3)若成绩在80分以下(含80分)的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有______人.
20.(本小题8分)
【项目式学习】为了测量某段河流的宽度，两个数学研学小组设计了不同的方案，他们在河南岸的点A处测得河北岸的数H恰好在A的正北方向.测量方案与数据如表：
请选择其中一个方案及其数据：
(1)求∠AHB的度数；
(2)求出河宽(精确到1m)．
参考数据：sin74°≈0.96，sin37°≈0.60，tan74°≈3.50，tan37°≈0.75．
21.(本小题10分)
在眉山市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元．
(1)求每台电脑、每台电子白板各多少万元？
(2)根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，且要求购进的电子白板不少于10台，请设计一种最省钱的方案，并说明理由．
22.(本小题10分)
如图，在Rt△ABC中，∠ACB=90°，以斜边AB上的中线CD为直径作⊙O，与AC、BC分别交于点M、N，与AB的另一个交点为E.过点N作NF⊥AB，垂足为F，连接AN交CD于H；其中AC=6，BC=8．
(1)求证：NF是⊙O的切线；
(2)求NF和DH的长．
23.(本小题11分)
(1)[问题探究]
如图1，在正方形ABCD中，对角线AC、BD相交于点O.点P是线段AO上一点(与点A、O不重合)，连结PD、PB．

①求证：△PDC≌△PBC；
②将线段DP绕点P逆时针旋转，点D落在BA的延长线上的点Q处.当点P在线段AO上运动时，∠DPQ的大小是否发生变化？请说明理由；
③探究AQ与OP的数量关系，并说明理由．
(2)[迁移探究]
如图2，将正方形ABCD换成菱形ABCD，且∠ABC=60°，其他条件不变.试探究AQ与CP的数量关系，并说明理由．
24.(本小题12分)
如图，抛物线与x轴交于A(−2,0)、B(4,0)两点，与y轴交于点C(0,4)，点P是抛物线上的动点．
(1)求该抛物线的解析式；
(2)当点P在直线BC的上方运动时，连接AP，交直线BC于点D，交y轴于点E．
①若△ABD的面积是△PBD面积的3倍，求点P的坐标；
②当CD=CE时，求CE的长；
(3)过点P作PF/​/y轴交直线BC于点F，在y轴上是否存在点Q，使得以P、F、C、Q为顶点的四边形是菱形，若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．
月用水量(吨)
4
5
6
户数
3
4
3
分数段
频数
频率
50.5−60.5
24
0.08
60.5−70.5
60
0.2
70.5−80.5
75
0.25
80.5−90.5
m
0.3
90.5−100.5
51
n
项目课题
测量河流宽度
测量工具
测量角度的仪器，皮尺等
测量小组
第一小组
第二小组
测量方案示意图
说明
点B，C在点A的正东方向
点B在点A的正东方向，点
C在点A的正西方向
数据
BC=200m，∠ABH=74°，∠ACH=37°
BC=311m，∠ABH=74°，∠ACH=37°