数学（浙江卷）-学易金卷：2024年中考考前押题密卷

这是一份数学（浙江卷）-学易金卷：2024年中考考前押题密卷，文件包含数学浙江卷全解全析docx、数学浙江卷参考答案及评分标准docx、数学浙江卷考试版A4docx、数学浙江卷考试版A3docx等4份试卷配套教学资源，其中试卷共45页， 欢迎下载使用。

（考试时间：120分钟 试卷满分：120分）
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷
一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
1．下列手机中的图标是轴对称图形的是（ ）
A．B．
C．D．
2．已知，则的值为（ ）
A．B．C．12D．18
3．下列运算结果正确的是（ ）
A．m2+m2＝2m4B．a2•a3＝a5
C．（mn2）3＝mn6D．m6÷m2＝m3
4．在五边形ABCDE中，∠A＝∠E＝120°，∠B＝130°，∠C＝70°，则∠D＝（ ）
A．100°B．110°C．120°D．130°
5．下列调查适合做普查的是（ ）
A．调查游客对我市景点的满意程度
B．调查我省中小学生的身高情况
C．调查九年级（3）班全班学生本周末参加社区活动的时间
D．调查我市中小学生保护水资源的意识
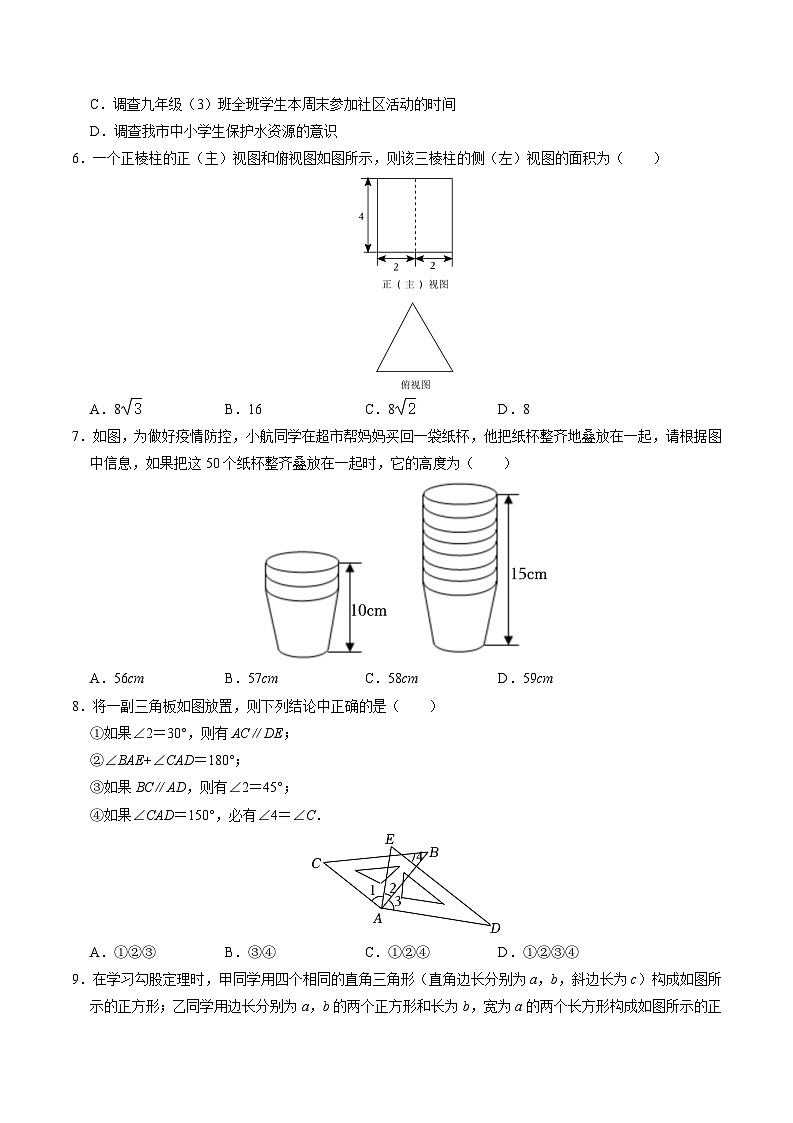
6．一个正棱柱的正（主）视图和俯视图如图所示，则该三棱柱的侧（左）视图的面积为（ ）
A．8B．16C．8D．8
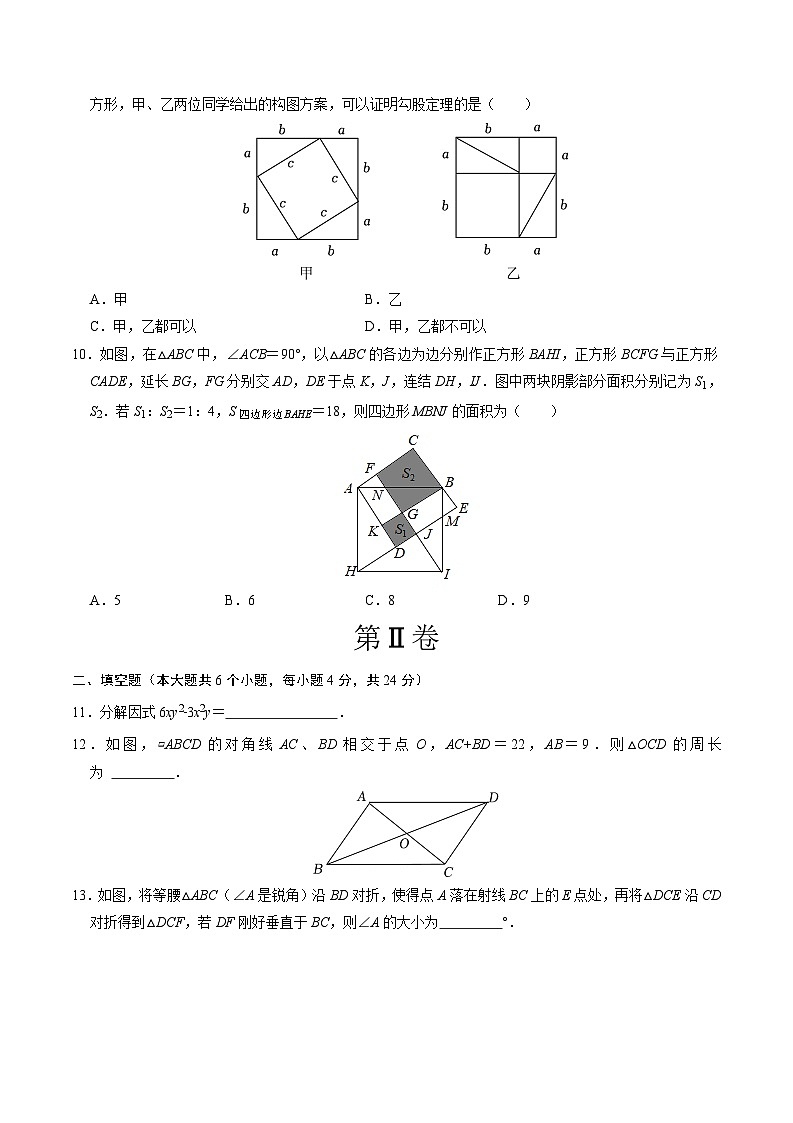
7．如图，为做好疫情防控，小航同学在超市帮妈妈买回一袋纸杯，他把纸杯整齐地叠放在一起，请根据图中信息，如果把这50个纸杯整齐叠放在一起时，它的高度为（ ）
A．56cmB．57cmC．58cmD．59cm
8．将一副三角板如图放置，则下列结论中正确的是（ ）
①如果∠2＝30°，则有AC∥DE；
②∠BAE+∠CAD＝180°；
③如果BC∥AD，则有∠2＝45°；
④如果∠CAD＝150°，必有∠4＝∠C．
A．①②③B．③④C．①②④D．①②③④
9．在学习勾股定理时，甲同学用四个相同的直角三角形（直角边长分别为a，b，斜边长为c）构成如图所示的正方形；乙同学用边长分别为a，b的两个正方形和长为b，宽为a的两个长方形构成如图所示的正方形，甲、乙两位同学给出的构图方案，可以证明勾股定理的是（ ）
A．甲B．乙
C．甲，乙都可以D．甲，乙都不可以
10．如图，在△ABC中，∠ACB＝90°，以△ABC的各边为边分别作正方形BAHI，正方形BCFG与正方形CADE，延长BG，FG分别交AD，DE于点K，J，连结DH，IJ．图中两块阴影部分面积分别记为S1，S2．若S1：S2＝1：4，S四边形边BAHE＝18，则四边形MBNJ的面积为（ ）
A．5B．6C．8D．9
第Ⅱ卷
二、填空题（本大题共6个小题，每小题4分，共24分）
11．分解因式6xy2﹣3x2y＝ ．
12．如图，▱ABCD的对角线AC、BD相交于点O，AC+BD＝22，AB＝9．则△OCD的周长为 ．
13．如图，将等腰△ABC（∠A是锐角）沿BD对折，使得点A落在射线BC上的E点处，再将△DCE沿CD对折得到△DCF，若DF刚好垂直于BC，则∠A的大小为 °．
14．已知一组数据x1，x2，x3，x4，x5的方差是，那么x1﹣5，x2﹣5，x3﹣5，x4﹣5，x5﹣5的方差是 ．
15．直线y＝kx+6k交x轴于点A，交y轴于点B，以原点O为圆心，3为半径的⊙O与l相交，则k的取值范围为 ．
16．在二次函数y＝x2﹣2tx+3中，t为大于0的常数．
（1）若此二次函数的图象过点（2，1），则t等于 ；
（2）如果A（m﹣2，a），B（4，b），C（m，a）都在此二次函数的图象上，且a＜b＜3，则m的取值范围是 ．
三、解答题（本大题共8个小题，共66分．解答应写出文字说明，证明过程或演算步骤）
17．（6分）以下是某同学化简分式的部分运算过程：
解：原式＝……第一步
＝第二步
＝．……第三步
……
（1）上面第二步计算中，中括号里的变形的依据是 ；
（2）上面的运算过程中第 步出现了错误；
（3）请你写出完整的正确解答过程，并从﹣2，2，0中选一个作为x的值代入求值．
18．（6分）如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（﹣1，5），B（﹣4，3），C（﹣2，2）．
（1）△A1B1C1与△ABC关于原点O成中心对称，画出△A1B1C1，并写出点A1，B1，C1的坐标；
（2）将△ABC绕原点O顺时针旋转90°得到△A2B2C2，画出△A2B2C2；
（3）求（2）的旋转过程中点C经过的路径长．
19．（6分）如图，在△ABC中，AB＝AC，点D，E，F分别在AB，BC，AC边上，且BE＝CF，BD＝CE．
（1）求证：∠BED＝∠CFE；
（2）当∠BAC＝44°时，求∠DEF的度数．
20．（8分）跳绳是驿城区某校体育活动的特色项目．体育组为了了解八年级学生1分钟跳绳次数情况，随机抽取20名八年级学生进行1分钟跳绳测试（单位：次），数据如下：
100 110 114 114 120 122 122 131 144 148
152 155 156 165 165 165 165 174 188 190
对这组数据进行整理和分析，结果如下：
请根据以上信息解答下列问题：
（1）填空：a＝ ，b＝ ．
（2）学校规定1分钟跳绳165次及以上为优秀，请你估计七年级500名学生中，约有多少名学生能达到优秀．
（3）某同学1分钟跳绳152次，请推测该同学的1分钟跳绳次数是否超过年级一半的学生？说明理由．
21．（8分）A、B两地相距120km，甲车从A地驶往B地，乙车从B地以80km/h的速度匀速驶往A地，乙车比甲车晚出发m h．设甲车行驶的时间为x（h），甲、乙两车离A地的距离分别为y1（km）、y2（km），图中线段OP表示y1与x的函数关系．
（1）甲车的速度为 km/h；
（2）若两车同时到达目的地，在图中画出y2与x的函数图象，并求甲车行驶几小时后与乙车相遇；
（3）若甲、乙两车在距A地60km至72km之间的某处相遇，直接写出m的范围．
22．（10分）某校八年级学生在数学课上进行了项目化学习研究，某小组研究如下：
【提出驱动性问题】机场监控问题．
【设计实践任务】选择“素材1”“素材2”，设计了“任务1”“任务2”“任务3”的实践活动．请你尝试帮助他们解决相关问题．
23．（10分）【操作与发现】
如图①，在正方形ABCD中，点N，M分别在边BC、CD上．连接AM、AN、MN．∠MAN＝45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而可得：DM+BN＝MN．
（1）【实践探究】在图①条件下，若CN＝6，CM＝8，则正方形ABCD的边长是 ．
（2）如图②，在正方形ABCD中，点M、N分别在边DC、BC上，连接AM、AN、MN，∠MAN＝45°，若tan∠BAN＝，求证：M是CD的中点．
（3）【拓展】如图③，在矩形ABCD中，AB＝12，AD＝16，点M、N分别在边DC、BC上，连接AM、AN，已知∠MAN＝45°，BN＝4，则DM的长是 ．
24．（12分）如图1，E点为x轴正半轴上一点，⊙E交x轴于A、B两点，交y轴于C、D两点，P点为劣弧上一个动点，且A（﹣1，0）、E（1，0）．
（1）的度数为 °；
（2）如图2，连结PC，取PC中点G，连结OG，则OG的最大值为 ；
（3）如图3，连接AC、AP、CP、CB．若CQ平分∠PCD交PA于Q点，求AQ的长；
（4）如图4，连接PA、PD，当P点运动时（不与B、C两点重合），求证：为定值，并求出这个定值．
平均数
众数
中位数
145
a
b
机场监控问题的思考
素材1
如图是某机场监控屏显示两飞机的飞行图象，1号指挥机（看成点P）始终以3km/min的速度在离地面5km高的上空匀速向右飞行．

素材2
2号试飞机（看成点Q）一直保持在1号机P的正下方从原点O处沿45°角爬升，到高4km的A处便立刻转为水平飞行，再过1min到达B处开始沿直线BC降落，要求1min后到达C（10，3）处．
问题解决
任务1
求解析式和速度
求出OA段h关于s的函数解析式，直接写出2号机的爬升速度；
任务2
求解析式和坐标
求出BC段h关于s的函数解析式，并预计2号机着陆点的坐标；
任务3
计算时长
通过计算说明两机距离PQ不超过3km的时长是多少．