2024成都中考数学二轮复习专题 PA+kPB型之阿氏圆问题专项训练（含答案）

这是一份2024成都中考数学二轮复习专题 PA+kPB型之阿氏圆问题专项训练（含答案），共36页。

模型来源
“阿氏圆”又称为“阿波罗尼斯圆”，如下图，已知A、B两点，点P满足PA：PB=k（k≠1），则满足条件的所有的点P的轨迹构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.
模型建立
如图 1 所示，⊙O 的半径为R，点 A、B 都在⊙O 外 ，P为⊙O上一动点，已知，连接 PA、PB，则当“”的值最小时，P 点的位置如何确定？

解决办法：如图2，在线段 OB 上截取OC使 OC=R，则可说明△BPO与△PCO相似，则有PB=PC。故本题求“PA+PB”的最小值可以转化为“PA+PC”的最小值，其中与A与C为定点，P为动点，故当 A、P、C 三点共线时，“PA+PC”值最小。
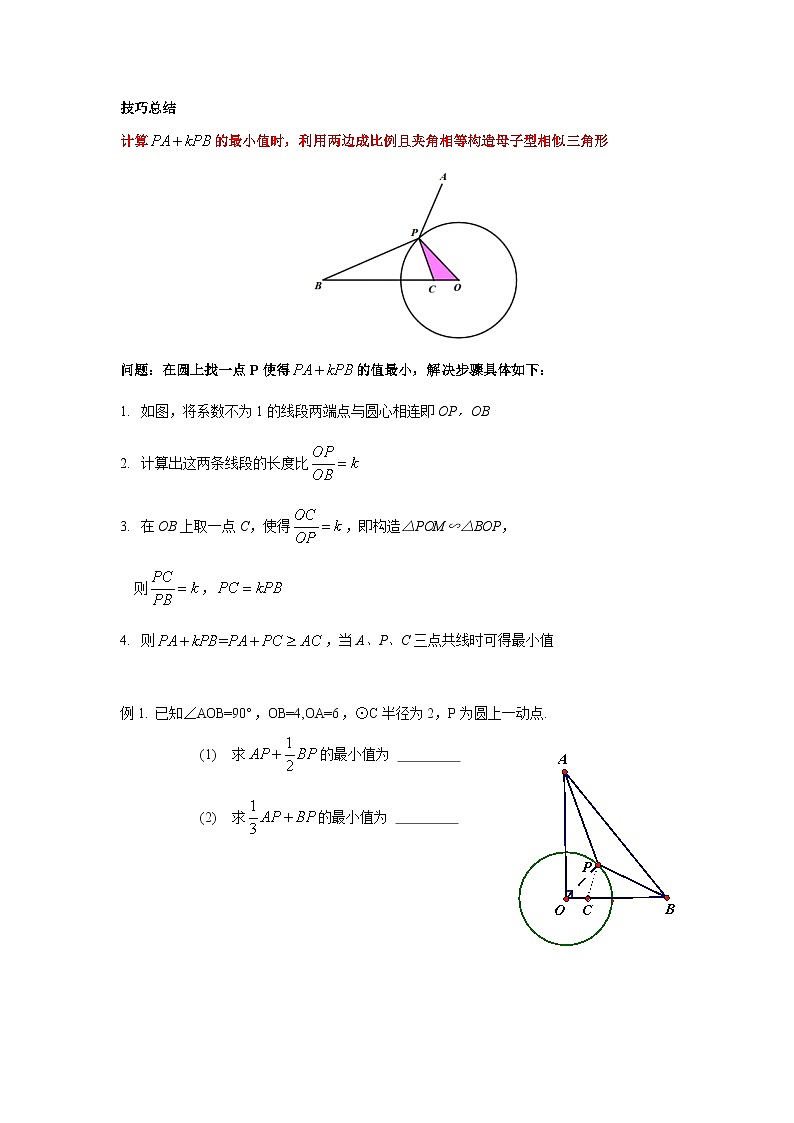
技巧总结
计算的最小值时，利用两边成比例且夹角相等构造母子型相似三角形
问题：在圆上找一点P使得的值最小，解决步骤具体如下：
如图，将系数不为1的线段两端点与圆心相连即OP，OB
计算出这两条线段的长度比
在OB上取一点C，使得，即构造△POM∽△BOP，
则，
则，当A、P、C三点共线时可得最小值
例1. 已知∠AOB=90°，OB=4,OA=6，⊙C半径为2，P为圆上一动点.
求的最小值为
求的最小值为
例2. 菱形边长为4，，点为边的中点，点为上一动点，连接、，并将沿翻折得△，连接，取的中点为点，连接，则最小值为 ．
例3.(1)如图1，已知正方形ABC的边长为4，圆B的半径为2，点P是圆B上的一个动点，求的最小值和的最大值.
(2)如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么的最小值为 ；的最大值为
(3)如图3，已知菱形ABCD的边长为4，∠B=60°，圆B的半径为2.点P是圆B上的一个动点.那么的最小值为 ；的最大值为
过关检测
1. 如图，点C坐标为(2,5)，点A的坐标为(7,0)，⊙C的半径为,点B在⊙C上一动点，的最小值为________.
2.如图，在RT△ABC中，∠B=90°,AB=CB=2，以点B为圆心作圆与AC相切，圆C的半径为，点P为圆B上的一动点，求的最小值.
3.如图，边长为4的正方形，内切圆记为⊙O，P是⊙O上一动点，则的最小值为________.
4.如图，等边△ABC的边长为6，内切圆记为⊙O，P是⊙O上一动点，则的最小值为________.
例4. 已知：如图1，抛物线与轴交于，两点，与轴交于点，点为顶点．
（1）求抛物线解析式及点的坐标；
（2）若直线过点，为直线上的动点，当以、、为顶点所作的直角三角形有．且只有三个时，求直线的解析式；
（3）如图2，为的中点，将线段绕点顺时针旋转得到，旋转角为，连接、，当取得最小值时，求直线与抛物线的交点坐标．
过关检测
1.如图，直线与轴、轴分别相交于、两点，抛物线经过点，交轴正半轴于点．
（1）求该抛物线的函数表达式；
（2）已知点是抛物线上的一个动点，并且点在第一象限内，连接、，设点的横坐标为，的面积为，求与的函数表达式，并求出的最大值及此时动点的坐标；
（3）将点绕原点旋转得点，连接、，在旋转过程中，一动点从点出发，沿线段以每秒3个单位的速度运动到，再沿线段以每秒1个单位长度的速度运动到后停止，求点在整个运动过程中用时最少是多少？
学习任务
1. 阅读以下材料，并按要求完成相应的任务．
已知平面上两点、，则所有符合且的点会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．
阿氏圆基本解法：构造三角形相似．
【问题】如图1，在平面直角坐标中，在轴，轴上分别有点，，点是平面内一动点，且，设，求的最小值．
阿氏圆的关键解题步骤：
第一步：如图1，在上取点，使得；
第二步：证明；第三步：连接，此时即为所求的最小值．
下面是该题的解答过程（部分）
解：在上取点，使得，
又，．
任务：
（1）将以上解答过程补充完整．
（2）如图2，在中，，，，为内一动点，满足，利用（1）中的结论，请直接写出的最小值．
2. 如图，在平面直角坐标系中，，，，，P是△AOB外部第一象限内的一动点，且∠BPA=135°，则的最小值是多少？
3. 如图，Rt△ABC，∠ACB＝90°，AC＝BC＝2，以C为顶点的正方形CDEF（C、D、E、F四个顶点按逆时针方向排列）可以绕点C自由转动，且CD＝，连接AF，BD
（1）求证：△BDC≌△AFC；
（2）当正方形CDEF有顶点在线段AB上时，直接写出BD+AD的值；
（3）直接写出正方形CDEF旋转过程中，BD+AD的最小值．
4. 如图，抛物线与直线交于，两点，直线交轴于点．点是直线上的动点，过点作轴交于点，交抛物线于点．
（1）求抛物线的表达式；
（2）连接，，当四边形是平行四边形时，求点的坐标；
（3）①在轴上存在一点，连接，，当点运动到什么位置时，以，，，为顶点的四边形是矩形？求出此时点，的坐标；
②在①的前提下，以点为圆心，长为半径作圆，点为上一动点，求它的最小值．
5. 如图1，抛物线与轴交于点，与轴交于点，在轴上有一动点，，过点作轴的垂线交直线于点，交抛物线于点，过点作于点．
（1）求的值和直线的函数表达式；
（2）设的周长为，的周长为，若，求的值；
（3）如图2，在（2）条件下，将线段绕点逆时针旋转得到，旋转角为，连接、，求的最小值．

2024成都中考数学二轮复习专题
PA+kPB型之阿氏圆问题专项训练（解析版）
课中讲解
模型来源
“阿氏圆”又称为“阿波罗尼斯圆”，如下图，已知A、B两点，点P满足PA：PB=k（k≠1），则满足条件的所有的点P的轨迹构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”.
模型建立
如图 1 所示，⊙O 的半径为R，点 A、B 都在⊙O 外 ，P为⊙O上一动点，已知R=OB，
连接 PA、PB，则当“PA+PB”的值最小时，P 点的位置如何确定？

解决办法：如图2，在线段 OB 上截取OC使 OC=R，则可说明△BPO与△PCO相似，则有PB=PC。故本题求“PA+PB”的最小值可以转化为“PA+PC”的最小值，其中与A与C为定点，P为动点，故当 A、P、C 三点共线时，“PA+PC”值最小。
技巧总结
计算的最小值时，利用两边成比例且夹角相等构造母子型相似三角形
问题：在圆上找一点P使得的值最小，解决步骤具体如下：
如图，将系数不为1的线段两端点与圆心相连即OP，OB
计算出这两条线段的长度比
在OB上取一点C，使得，即构造△POM∽△BOP，则，
则，当A、P、C三点共线时可得最小值
例1. 已知∠AOB=90°，OB=4,OA=6，⊙C半径为2，P为圆上一动点.
求的最小值为
求的最小值为
第（1）问解题基本步骤：构造△OPC∽△OBP,则（相似比）
= 1 \* GB3 ①分别连接圆心O与系数不为1的线段BP的两端点，即OP，OB;
= 2 \* GB3 ②计算的值，则（）
= 3 \* GB3 ③计算OC的长度，由得：（相似比×半径）
= 4 \* GB3 ④连接AC，当A、P、C三点共线时，
= 5 \* GB3 ⑤计算AC的长度即为最小值.
例2. 菱形边长为4，，点为边的中点，点为上一动点，连接、，并将沿翻折得△，连接，取的中点为点，连接，则最小值为 ．
【分析】过点作交的延长线于，取的中点，连接，在上截取，使得，连接，．利用相似三角形的性质证明，求出的长即可解决问题．
【解答】解：过点作交的延长线于，取的中点，连接，在上截取，使得，连接，．
，由翻折的性质可知，，
，，，
，，，，
，，，
，
四边形是菱形，，，
，
，，，
，
，
，
的最小值为．
故答案为．
【点评】本题考查菱形的性质，解直角三角形，相似三角形的判定和性质，两点之间线段最短等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，学会用转化的思想思考问题，属于中考填空题中的压轴题．
例3. （1）如图1，已知正方形ABC的边长为4，圆B的半径为2，点P是圆B上的一个动点，求的最小值和的最大值.
(2)如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么的最小值为 ；的最大值为
（3）如图3，已知菱形ABCD的边长为4，∠B=60°，圆B的半径为2.点P是圆B上的一个动点.那么的最小值为 ；的最大值为
【解答】解：（1）如图3中，在BC上取一点G，使得BG＝4．
∵＝＝，＝＝，
∴＝，∵∠PBG＝∠PBC，
∴△PBG∽△CBP，
∴＝＝，∴PG＝PC，
∴PD+PC＝DP+PG，
∵DP+PG≥DG，
∴当D、G、P共线时，PD+PC的值最小，最小值为DG＝＝．
∵PD﹣PC＝PD﹣PG≤DG，
当点P在DG的延长线上时，PD﹣PC的值最大，最大值为DG＝．
故答案为，
（2）如图4中，在BC上取一点G，使得BG＝1，作DF⊥BC于F．
∵＝＝2，＝＝2，
∴＝，∵∠PBG＝∠PBC，
∴△PBG∽△CBP，
∴＝＝，
∴PG＝PC，
∴PD+PC＝DP+PG，
∵DP+PG≥DG，∴当D、G、P共线时，PD+PC的值最小，最小值为DG，
在Rt△CDF中，∠DCF＝60°，CD＝4，
∴DF＝CD•sin60°＝2，CF＝2，
在Rt△GDF中，DG＝＝
∵PD﹣PC＝PD﹣PG≤DG，
当点P在DG的延长线上时，PD﹣PC的值最大（如图2中），最大值为DG＝．
故答案为，．
过关检测
1. 如图，点C坐标为(2,5)，点A的坐标为(7,0)，⊙C的半径为,点B在⊙C上一动点，的最小值为________.
[答案]：5.
2. 如图，在Rt△ABC中，∠1. 如图，在RT△ABC中，∠B=90°，AB=CB=2，以点B为圆心作圆与AC相切，圆C的半径为，点P为圆B上的一动点，求的最小值.
[答案]：.
3. 如图，边长为4的正方形，内切圆记为⊙O，P是⊙O上一动点，则PA+PB的最小值为________.
[答案]：.
4. 如图，等边△ABC的边长为6，内切圆记为⊙O，P是⊙O上一动点，则2PB+PC的最小值为________.
[答案]：.
例4. 已知：如图1，抛物线与轴交于，两点，与轴交于点，点为顶点．
（1）求抛物线解析式及点的坐标；
（2）若直线过点，为直线上的动点，当以、、为顶点所作的直角三角形有．且只有三个时，求直线的解析式；
（3）如图2，为的中点，将线段绕点顺时针旋转得到，旋转角为，连接、，当取得最小值时，求直线与抛物线的交点坐标．
【分析】（1）由抛物线的交点式可知抛物线的解析式为，通过整理可得到抛物线的解析式，然后利用配方法可得到抛物线的定点坐标；
（2）过点、分别作轴的垂线，这两条垂线与直线总是有交点的，即2个点．以为直径的如果与直线相交，那么就有2个点；如果圆与直线相切，就只有1个点了，以为直径作，作与相切，则，过作，先求得点的坐标，于是可求得的解析式，由图形的对称性可知点的坐标还可以是，，然后可求得另一种情况；
（3）取使，连接，接下来，证明△，从而可得到，故此当、、在一条直线上时，有最小值，最后，依据勾股定理求得的长度即可．
【解答】解：（1）抛物线与轴交于，两点，
．
，抛物线的顶点坐标为．
（2）过点、分别作轴的垂线，这两条垂线与直线总是有交点的，即2个点．
以为直径的如果与直线相交，那么就有2个点；如果圆与直线相切，就只有1个点了．
如图所示：以为直径作，作与相切，则，过作．
，，．．
又，．，，
．点的坐标为，．
设的解析式为，则，解得：，，
直线的解析式为．
由图形的对称性可知：当直线经过点，时，直线与相切，则，解得：，，
直线的解析式为．
综上所述，直线的解析式为或．
（3）如图所示：取使，连接．
，，，，．
又，△，．．
，
当、、在一条直线上时，有最小值，
直线的解析式为，
由，解得或，
直线与抛物线的交点坐标为，．
【点评】本题考查二次函数综合题、相似三角形的判定和性质、锐角三角函数等知识，解题的关键是确定出取得最小值的条件．
过关检测
1.如图，直线与轴、轴分别相交于、两点，抛物线经过点，交轴正半轴于点．
（1）求该抛物线的函数表达式；
（2）已知点是抛物线上的一个动点，并且点在第一象限内，连接、，设点的横坐标为，的面积为，求与的函数表达式，并求出的最大值及此时动点的坐标；
（3）将点绕原点旋转得点，连接、，在旋转过程中，一动点从点出发，沿线段以每秒3个单位的速度运动到，再沿线段以每秒1个单位长度的速度运动到后停止，求点在整个运动过程中用时最少是多少？
【分析】（1）根据题意可以求得点的坐标，从而可以求得抛物线的解析式；
（2）根据题意可以求得点的坐标，然后根据题意和图形可以用含的代数式表示出，然后将其化为顶点式，再根据二次函数的性质即可解答本题；
（3）根据题意作出点，然后利用三角形相似和勾股定理、两点之间线段最短即可求得的最小值．
【解答】解：（1）将代入，得，点的坐标为，
抛物线经过点，，得，
抛物线的解析式为：；
（2）将代入，得，，点的坐标为，
点是抛物线上的一个动点，并且点在第一象限内，点的横坐标为，
，点的坐标为，
将代入，得，点的坐标，
的面积为，
，
化简，得，
当时，取得最大值，此时，此时点的坐标为，，
即与的函数表达式是，的最大值是，此时动点的坐标是，；
（3）如右图所示，取点的坐标为，连接、，
，，，△，
，即，
，
，
即点在整个运动过程中用时最少是秒．

【点评】这是一道二次函数综合题，主要考查二次函数的最值、最短路径、三角形相似，待定系数法求二次函数解析式，解答本题的关键是明确题意，找出所求问题需要的条件，作出合适的辅助线，利用数形结合的思想和转化的数学思想解答．

学习任务
1. 阅读以下材料，并按要求完成相应的任务．
已知平面上两点、，则所有符合且的点会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．
阿氏圆基本解法：构造三角形相似．
【问题】如图1，在平面直角坐标中，在轴，轴上分别有点，，点是平面内一动点，且，设，求的最小值．
阿氏圆的关键解题步骤：
第一步：如图1，在上取点，使得；
第二步：证明；第三步：连接，此时即为所求的最小值．
下面是该题的解答过程（部分）
解：在上取点，使得，
又，．
任务：
（1）将以上解答过程补充完整．
（2）如图2，在中，，，，为内一动点，满足，利用（1）中的结论，请直接写出的最小值．
【解答】解（1）在上取点，使得，
又，．，，
，当取最小值时，有最小值，即，，三点共线时有最小值，
利用勾股定理得．
（2），，在上取一点，使得，
的最小值为．
【点评】本题属于相似形综合题，考查了相似三角形的判定和性质，勾股定理，两点之间线段最短等知识，解题的关键是理解题意，学会用转化的思想思考问题，属于中考常考题型．
2.如图，在平面直角坐标系中，，，，，P是△AOB外部第一象限内的一动点，且∠BPA=135°，则的最小值是多少？
[答案]
3.如图，Rt△ABC，∠ACB＝90°，AC＝BC＝2，以C为顶点的正方形CDEF（C、D、E、F四个顶点按逆时针方向排列）可以绕点C自由转动，且CD＝，连接AF，BD
（1）求证：△BDC≌△AFC；
（2）当正方形CDEF有顶点在线段AB上时，直接写出BD+AD的值；
（3）直接写出正方形CDEF旋转过程中，BD+AD的最小值．
【解答】（1）证明：如图1中，
∵四边形CDEF是正方形，
∴CF＝CD，∠DCF＝∠ACB＝90°，
∴∠ACF＝∠DCB，
∵AC＝CB，
∴△FCA≌△DCB（SAS）．
（2）解：①如图2中，当点D，E在AB边上时，
∵AC＝BC＝2，∠ACB＝90°，
∴AB＝2，
∵CD⊥AB，
∴AD＝BD＝，
∴BD+AD＝+1．
②如图3中，当点E，F在边AB上时．
BD＝CF＝，AD＝＝，
∴BD+AD＝+．
（3）如图4中．取AC的中点M．连接DM，BM．
∵CD＝，CM＝1，CA＝2，
∴CD2＝CM•CA，
∴＝，∵∠DCM＝∠ACD，
∴△DCM∽△ACD，
∴＝＝，
∴DM＝AD，
∴BD+AD＝BD+DM，
∴当B，D，M共线时，BD+AD的值最小，
最小值＝＝．
4. 如图，抛物线与直线交于，两点，直线交轴于点．点是直线上的动点，过点作轴交于点，交抛物线于点．
（1）求抛物线的表达式；
（2）连接，，当四边形是平行四边形时，求点的坐标；
（3）①在轴上存在一点，连接，，当点运动到什么位置时，以，，，为顶点的四边形是矩形？求出此时点，的坐标；
②在①的前提下，以点为圆心，长为半径作圆，点为上一动点，求它的最小值．
【解答】解：（1）点，在抛物线上，
，，抛物线的解析式为；
（2）设直线的解析式为过点，，
，，直线的解析式为，
设，，
四边形是平行四边形，，
，
．
（3）①如图1，
由（2）知，直线的解析式为，设，
直线，，
设，
以点，，，为顶点的四边形是矩形，
直线的解析式为，直线，
，为对角线，与互相平分，
，，
，，．；
②如图2，
由①知，，，，
，，
设交于，取的中点，，
连接交于，连接，
，，
，，，
，，，
的最小值，
设点，
，，
，，或（由于，所以舍去），
，，
，，
即：．
【点评】此题是二次函数综合题，主要考查了待定系数法，平行四边形的性质，矩形的性质，相似三角形的判定和性质，中点坐标公式，极值的确定，解（1）的关键是掌握待定系数法，解（2）的关键是利用平行四边形的对边相等建立方程求解，解（3）①的关键是利用中点坐标公式建立方程求解，解（3）②的关键是构造相似三角形，是一道中等难度的题目．
5. 如图1，抛物线与轴交于点，与轴交于点，在轴上有一动点，，过点作轴的垂线交直线于点，交抛物线于点，过点作于点．
（1）求的值和直线的函数表达式；
（2）设的周长为，的周长为，若，求的值；
（3）如图2，在（2）条件下，将线段绕点逆时针旋转得到，旋转角为，连接、，求的最小值．
【分析】（1）令，求出抛物线与轴交点，列出方程即可求出，根据待定系数法可以确定直线解析式．
（2）由，推出，列出方程即可解决问题．
（3）在轴上 取一点使得，构造相似三角形，可以证明就是的最小值．
【解答】解：（1）令，则，，或，
抛物线与轴交于点，，．
，，
设直线解析式为，则，解得，
直线解析式为．
（2）如图1中，
，，，，
，，
，，，
抛物线解析式为，
，，解得或4，
经检验是分式方程的增根，．
（3）如图2中，在轴上 取一点使得，连接，在上取一点使得．
，，，
，，
△△，，
，
，此时最小（两点间线段最短，、、共线时），
最小值．
【点评】本题考查相似三角形的判定和性质、待定系数法、最小值问题等知识，解题的关键是构造相似三角形，找到线段就是的最小值，属于中考压轴题．
6. 如图，顶点为的抛物线经过点和轴正半轴上的点，连接、、，已知，．
（1）求这条抛物线的表达式；
（2）过点作，垂足为，点为轴上的动点，若以、、为顶点的三角形与相似，求点的坐标；
（3）若将（2）的线段绕点逆时针旋转得到，旋转角为，连接、，求的最小值．
【分析】（1）根据，，求出点坐标，以及点坐标，进而利用待定系数法求二次函数解析式；
（2），由，，推出当或时，与相似；
（3）如图，取，．连接，．由△，推出，推出，推出，由，推出的最小值就是线段的长；
【解答】解：（1）过点作轴于点，
，，，，，
点坐标为：，点坐标为：，
将两点代入得：，解得：，
抛物线的表达式为：；
（2）如图，
，，，，
，，
，，
当或时，与相似，
，，
点坐标为或．
（3）如图，取，．连接，．
，，
△，，，
，
，
的最小值就是线段的长，最小值为．
家长签字：____________