

2024年安徽六安霍邱县中考模拟数学试卷
展开朝可能阻碍多。
2024年安徽六安霍邱县中考模拟数学试卷
一、单选题
1.下列各数中,最大的数是(
)
A.
B. 0
C. 1
D.
D.
2.下列算式中,计算结果为
A.
的是(
)
B.
C.
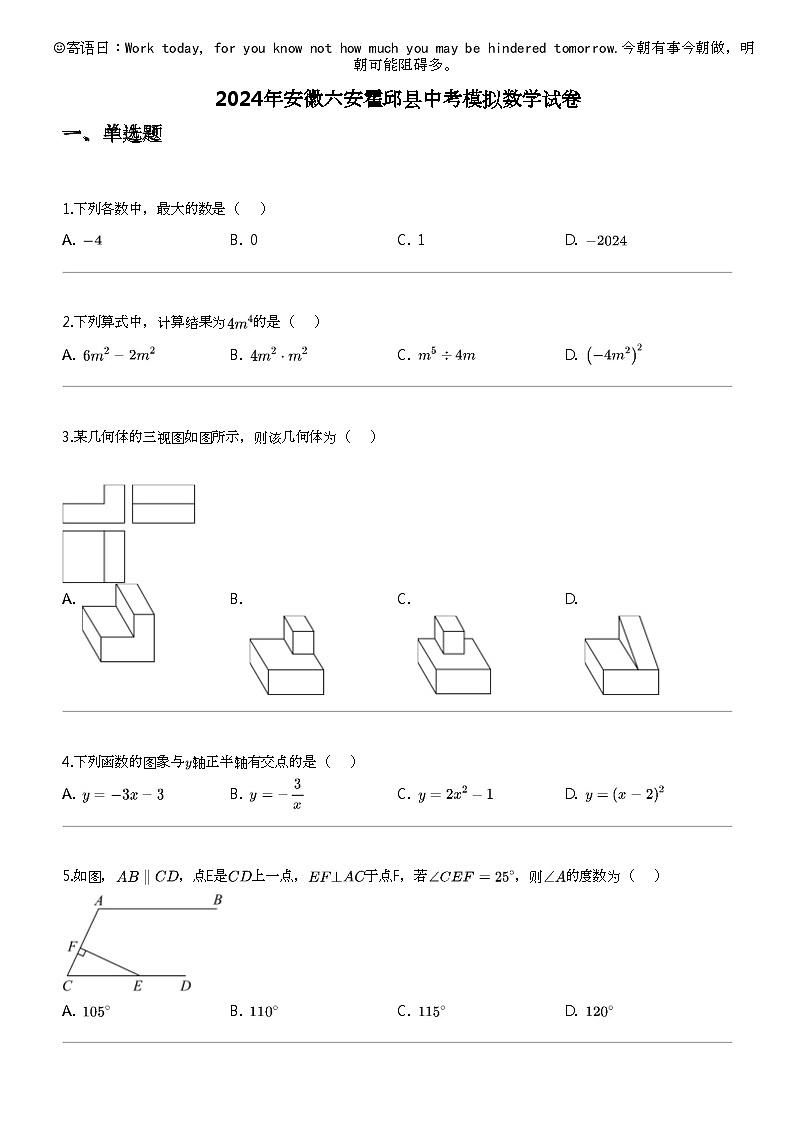
3.某几何体的三视图如图所示,则该几何体为(
)
A.
B.
C.
D.
4.下列函数的图象与 轴正半轴有交点的是(
)
A.
B.
C.
D.
5.如图,
,点E是
上一点,
于点F,若
,则
的度数为(
)
A.
B.
C.
D.
6.如图是甲、乙两人手中的扑克牌,两人随机出一张牌,记甲、乙牌中的数分别为m,n,使得
的概率为(
)
A.
B.
C.
D.
7.如图,在半径为5的
(
中,弦
与弦
互相垂直,垂足为点E,如果
,那么
的长为
)
A.
B. 3
C. 4
D.
8.某科技公司计划用两年时间使年生产总值增加到目前的4倍,并且使第二年的增长率是第一年增长率的2倍,
设第一年的增长率为x,则可列方程为(
)
A.
B.
C.
D.
9.函数
A.
与
的图象可能是(
C.
)
B.
D.
10.在
中,
是
边上的高,
是
边上的中线,
C. 3或
.若
,
,则
的值为(
)
A. 2或
B. 2或
D. 3或
二、填空题
11.2023年合肥常住人口达到985.3万人,“985.3万”用科学记数法表示为
.
12.若
,则整数n的值是
.
13.如图,四边形
.
内接于
,
,
与
分别相切于A,C,若
,则
14.如图,在菱形
中,点P是
上一点,将
沿着
折叠,得到
,连接
.
(1)若
,
,则
的度数为
,则 的最小值为
;
(2)点Q是
的中点,若
,
.
三、解答题
15.解不等式:
.
16.如图,在由边长为1个单位长度的小正方形组成的网格中,已知
务.
的顶点都在网格上,完成下列任
(1)将
(2)以点 为旋转中心,将(1)中
(3)在(1)(2)的条件下,利用网格点和无刻度的直尺画出线段
向右平移4个单位长度,再向下平移4个单位长度,得到
按顺时针方向旋转 ,得到
的中点P.
,画出
;
,画出
;
17.我国古代数学著作《张丘建算经》中著名的“百鸡问题”叙述如下:“鸡翁一,值钱五;鸡母一,值钱
三;鸡雏三,值钱一;百钱买百鸡,则翁、母、雏各几何?”意思是公鸡五钱一只,母鸡三钱一只,小鸡一钱
三只,要用一百钱买一百只鸡,问公鸡、母鸡、小鸡各多少只?若现已知小鸡买78只,求公鸡、母鸡各买几
只.
18.观察下列等式:
第1个等式:
第2个等式:
第3个等式:
第4个等式:
;
;
;
;
……
按照以上规律,解答下列问题:
(1)写出第5个等式:___________________________;
(2)写出你猜想的第n个等式:______________________________(用含n的等式表示),并证明.
19.某数学兴趣小组测量太湖山国家森林公园内望江塔
直,望江塔 与斜坡 之间的距离 长为14米,测得斜坡
D处有一个测角仪 ,从点E测得塔顶点A的仰角为
的高度,如图,已知望江塔
的坡度 ,斜坡
,已知测角仪
与水平地面
垂
长为 米,坡顶
长为 米,求望江塔
, ,
,
的高度.(精确到1米,图中所有点都在同一平面,参考数据:
)
20.如图,在平面直角坐标系
中,直线
与反比例函数
的图象交于
、B两点,与x
轴交于点
,与y轴交于点D.
(1)求a,k的值;
(2)求
的面积;
(3)根据图象,直接写出反比例函数值小于一次函数值时x的取值范围.
21.某学校组织开展主题为“节约用水,共建绿色校园”的社会实践活动.在关于节约用水知识测试中,随机
在七年级和八年级分别抽取20名同学进行相关知识测试(满分100分),统计他们的测试成绩(x),并绘制
相关统计图(不完整),请你根据以下相关信息完成下列任务.
信息1
七年级成绩:84,78,98,92,98,92,69,92,89,89,85,84,83,79,92,79,83,78,92,
58.
信息2
八年级成绩在
信息3
之间的数据为:89,88,85,81.
七年级抽取同学的成绩频数分布直方图和八年级抽取同学的成绩频数分布扇形统计图如下:
(1)填空:
___________,并补全七年级抽取同学的成绩频数分布直方图;
(2)请你补全七年级和八年级抽取同学的成绩数据的特征表:
平均数
84.7
众数
96
中位数
84.5
方差
67.21
183.68
七年级
八年级
①________
83.7
②________
(3)请根据上述统计图表中的信息,分析哪个年级对节约用水相关知识掌握的较好,说明理由.
22.如图,抛物线
经过
,
两点.
(1)求抛物线的函数表达式;
(2)点C为直线
上方抛物线上一动点,过点C作
,垂足为点D,作
轴,交
于点E,求
的最大值及此时点C的坐标.
23.在矩形
中,E是
上一点,连接
,
,
平分
.
(1)如图1,求证:
;
(2)如图2,取
中点F,连接
,
,
,
与
交于点G.
①求
②若
的度数;
,
,求
的长.
2024年安徽省六安市霍邱县中考模拟预测数学试题: 这是一份2024年安徽省六安市霍邱县中考模拟预测数学试题,共9页。
2024年安徽省六安市霍邱县中考模拟预测数学试题: 这是一份2024年安徽省六安市霍邱县中考模拟预测数学试题,共5页。
13,2024年安徽省六安市霍邱县中考模拟预测数学试题: 这是一份13,2024年安徽省六安市霍邱县中考模拟预测数学试题,共5页。












